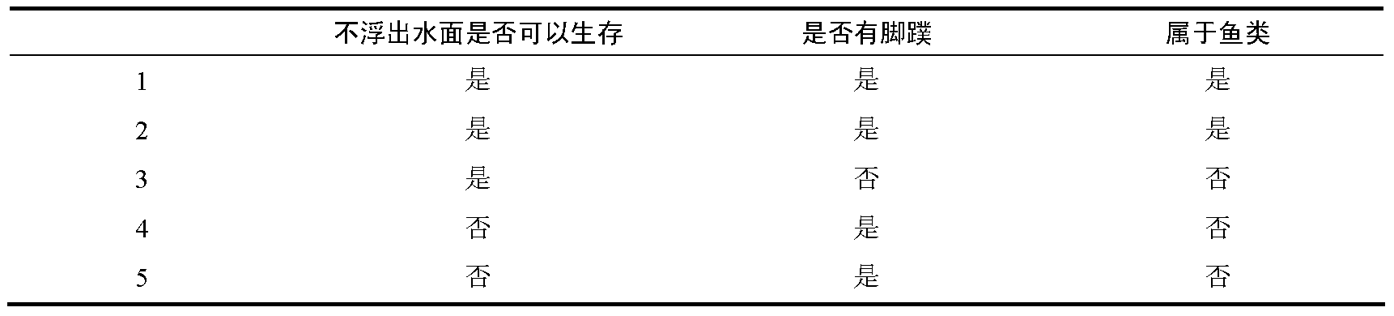
一、决策树到底是啥?
你可以把决策树想象成一棵 "问答树":从最顶端的根节点开始,问一个关于数据特征的问题(比如 "天气好吗?"),根据答案走不同的分支,一路问下去,直到走到最底端的叶子节点,那里就是最终的决策结果
根节点:第一个问题(比如 "今天天气怎么样?"),是整个决策的起点。
中间节点:路上的每个小问题(比如 "湿度高不高?""有没有风?"),负责进一步细分情况。
叶子节点:最终答案(比如 "去打球""在家学习"),所有数据最后都会落到这里。
二、怎么用决策树做预测?
决策树的使用分两步,测试阶段很简单,训练阶段是难点。
测试(用树做预测):就像查地图找路。比如给一个新数据 "晴天、湿度低、没风",从根节点开始问:"天气是晴天吗?"→ 走晴天分支;再问 "湿度高吗?"→ 走湿度低分支;最后问 "有风吗?"→ 走没风分支,最终落到 "去打球" 的叶子节点,这就是预测结果。
训练(造一棵能用的树):难就难在怎么确定 "先问哪个问题""接下来问什么"。总不能随便选个特征就开始问吧?得有科学的标准,这就是下面要讲的 "熵" 和 "信息增益"。
三、怎么选最好的问题(特征)?
核心问题:每次该选哪个特征当 "当前节点的问题"?答案是:选那个能把数据 "分最清楚" 的特征。这里需要两个工具:熵和信息增益。
- 熵:衡量数据 "乱不乱"
熵就像一把 "混乱程度尺子"。数据越乱(类别混杂),熵值越高;数据越整齐(大部分是同一类),熵值越低。
举个例子:
A 组数据:8 个 "是"、2 个 "否"→ 大部分是一类,不乱,熵值低。
B 组数据:5 个 "是"、5 个 "否"→ 一半一半,特别乱,熵值高。
极端情况:如果全是 "是"(或全是 "否"),熵值为 0(完全不乱);如果刚好一半一半,熵值最大(最乱)。
- 信息增益:选 "分乱效果最好" 的特征
先算原始数据的熵(一开始有多乱)。
用某个特征把数据分成几堆,算每堆的熵,再按每堆的大小加权平均,得到 "分完之后的总混乱度"。
信息增益 = 原始混乱度 - 分完后的混乱度。
哪个特征的信息增益大,就先选它当当前节点的问题。比如文档中 "14 天打球" 的例子,算出来 "天气" 这个特征的信息增益最大,所以根节点就问 "天气怎么样?"
训练: