《算法导论》第 30 章：多项式与快速傅里叶变换（FFT）

啊阿狸不会拉杆2025-08-20 8:39

大家好！今天我们深入拆解《算法导论》第 30 章 ------多项式与快速傅里叶变换（FFT）。这一章是算法效率优化的经典案例：多项式乘法的时间复杂度从朴素的(O(n^2))骤降到(O(n\log n))，而 FFT 正是实现这一飞跃的核心工具。

无论是数字信号处理（音频 / 图像压缩）、大整数乘法，还是机器学习中的卷积运算，FFT 都扮演着关键角色。本文会按照 "概念→案例→代码" 的逻辑，用通俗的语言 + 可直接运行的 C++ 代码，帮你彻底吃透这一章。

30.1 多项式的表示

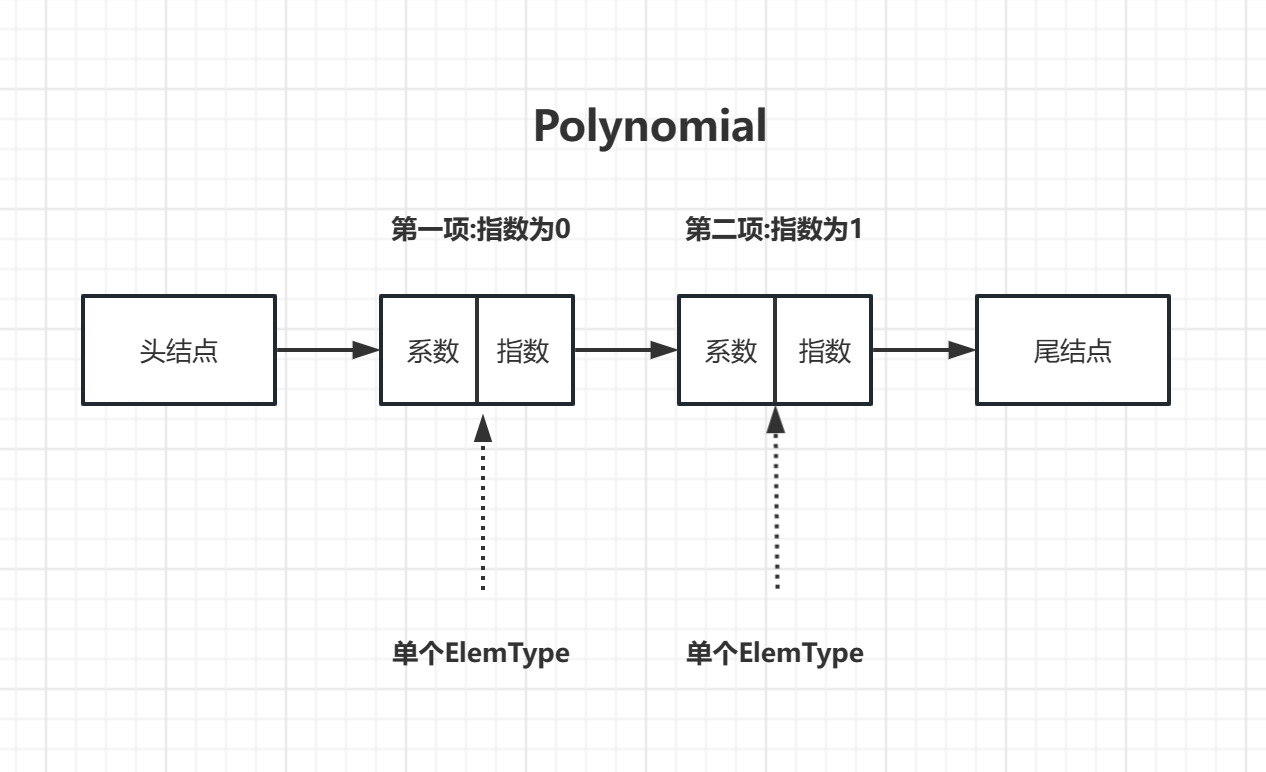
多项式的核心是 "如何存储"，不同的存储方式直接决定了运算效率。我们先对比两种主流表示法，再用代码实现关键运算。

30.1.1 两种表示法对比

假设多项式为 (A(x) = a_0 + a_1x + a_2x^2 + ... + a_{n-1}x^{n-1})（次数界为n），两种表示法的差异如下：

表示法 存储内容 加法时间复杂度 乘法时间复杂度 适用场景
系数表示法 系数数组 ([a_0,a_1,...,a_{n-1}]) (O(n)) (O(n^2)) 多项式加法、求值
点值表示法 点值对 ({(x_0,A(x_0)),(x_1,A(x_1)),..., (x_{n-1},A(x_{n-1}))}) (O(n)) (O(n)) 多项式乘法、插值

关键结论：

  • 系数表示法适合加法，但乘法慢；
  • 点值表示法适合乘法，但需要先把系数转成点值（靠 DFT），乘法后再转回来（靠逆 DFT）。

30.1.2 系数表示法的核心运算

系数表示法的加法很简单：对应系数相加；

乘法是 "卷积"（每个系数(a_i)乘(b_j)，加到结果的(i+j)位置）。

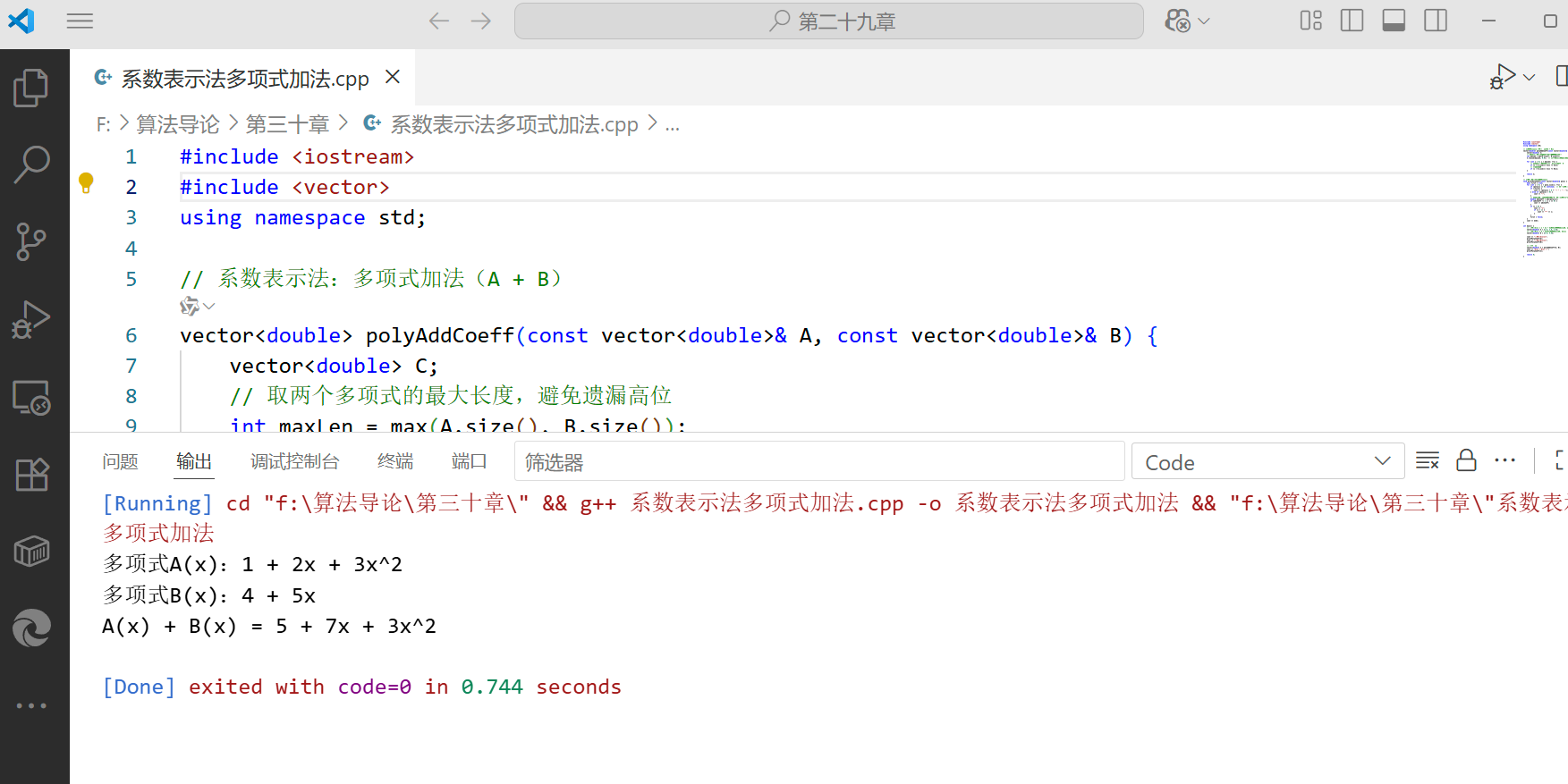
案例 1：系数表示法的多项式加法

问题：计算 (A(x) = 1 + 2x + 3x^2) 与 (B(x) = 4 + 5x) 的和。

预期结果：(C(x) = 5 + 7x + 3x^2)

复制代码 
#include <iostream>
#include <vector>
using namespace std;

// 系数表示法：多项式加法（A + B）
vector<double> polyAddCoeff(const vector<double>& A, const vector<double>& B) {
    vector<double> C;
    // 取两个多项式的最大长度，避免遗漏高位
    int maxLen = max(A.size(), B.size());
    C.resize(maxLen, 0.0);  // 初始化结果数组，默认系数为0

    for (int i = 0; i < maxLen; ++i) {
        // 若A的当前索引存在，加A[i]；否则加0
        if (i < A.size()) C[i] += A[i];
        // 同理处理B
        if (i < B.size()) C[i] += B[i];
    }

    return C;
}

// 打印多项式（系数表示法）
void printPolyCoeff(const vector<double>& poly) {
    bool first = true;
    for (int i = 0; i < poly.size(); ++i) {
        if (poly[i] == 0) continue;  // 跳过系数为0的项
        if (!first) {
            cout << (poly[i] > 0 ? " + " : " - ");
        } else if (poly[i] < 0) {
            cout << "-";
        }
        // 处理系数和x的次数（如x^0简化为常数，x^1简化为x）
        double absCoeff = abs(poly[i]);
        if (absCoeff != 1 || i == 0) {
            cout << absCoeff;
        }
        if (i > 0) {
            cout << "x";
            if (i > 1) {
                cout << "^" << i;
            }
        }
        first = false;
    }
    cout << endl;
}

int main() {
    // 多项式A(x) = 1 + 2x + 3x²（系数数组：[a0, a1, a2]）
    vector<double> A = {1.0, 2.0, 3.0};
    // 多项式B(x) = 4 + 5x（系数数组：[b0, b1]）
    vector<double> B = {4.0, 5.0};

    cout << "多项式A(x)：";
    printPolyCoeff(A);
    cout << "多项式B(x)：";
    printPolyCoeff(B);

    // 计算加法
    vector<double> C = polyAddCoeff(A, B);
    cout << "A(x) + B(x) = ";
    printPolyCoeff(C);

    return 0;
}

编译运行 ： 命令：g++ poly_coeff.cpp -o poly_coeff -std=c++11 输出：

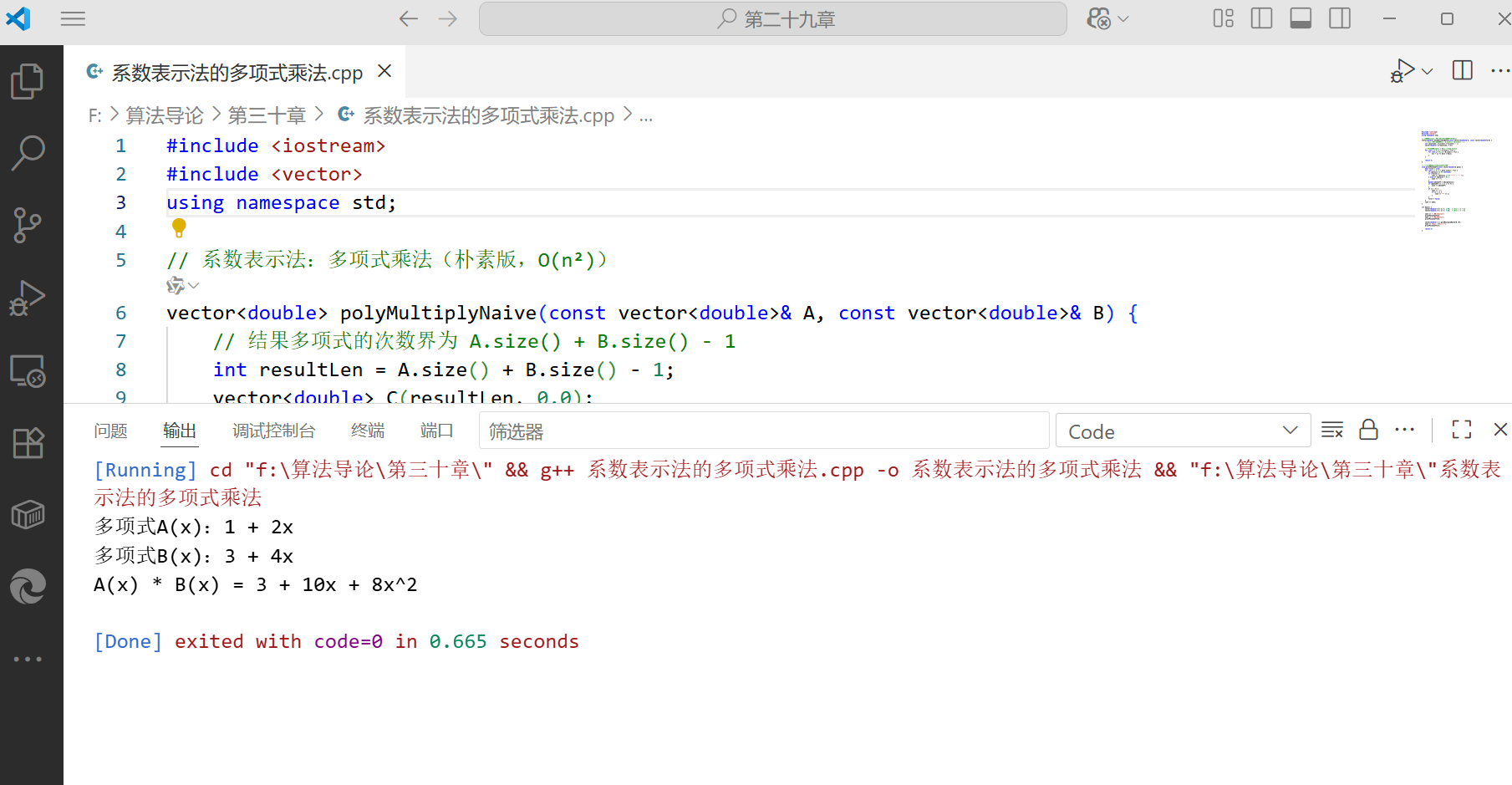
案例 2：系数表示法的多项式乘法（朴素版）

问题：计算 (A(x) = 1 + 2x) 与 (B(x) = 3 + 4x) 的积。

预期结果：(C(x) = 3 + 10x + 8x^2)

复制代码 
#include <iostream>
#include <vector>
using namespace std;

// 系数表示法：多项式乘法（朴素版，O(n²)）
vector<double> polyMultiplyNaive(const vector<double>& A, const vector<double>& B) {
    // 结果多项式的次数界为 A.size() + B.size() - 1
    int resultLen = A.size() + B.size() - 1;
    vector<double> C(resultLen, 0.0);

    // 卷积核心：A[i] * B[j] 贡献到 C[i+j]
    for (int i = 0; i < A.size(); ++i) {
        for (int j = 0; j < B.size(); ++j) {
            C[i + j] += A[i] * B[j];
        }
    }

    return C;
}

// 复用上面的printPolyCoeff函数
void printPolyCoeff(const vector<double>& poly) {
    bool first = true;
    for (int i = 0; i < poly.size(); ++i) {
        if (poly[i] == 0) continue;
        if (!first) {
            cout << (poly[i] > 0 ? " + " : " - ");
        } else if (poly[i] < 0) {
            cout << "-";
        }
        double absCoeff = abs(poly[i]);
        if (absCoeff != 1 || i == 0) {
            cout << absCoeff;
        }
        if (i > 0) {
            cout << "x";
            if (i > 1) {
                cout << "^" << i;
            }
        }
        first = false;
    }
    cout << endl;
}

int main() {
    vector<double> A = {1.0, 2.0};  // A(x) = 1 + 2x
    vector<double> B = {3.0, 4.0};  // B(x) = 3 + 4x

    cout << "多项式A(x)：";
    printPolyCoeff(A);
    cout << "多项式B(x)：";
    printPolyCoeff(B);

    vector<double> C = polyMultiplyNaive(A, B);
    cout << "A(x) * B(x) = ";
    printPolyCoeff(C);

    return 0;
}

运行输出：

30.2 DFT 与 FFT

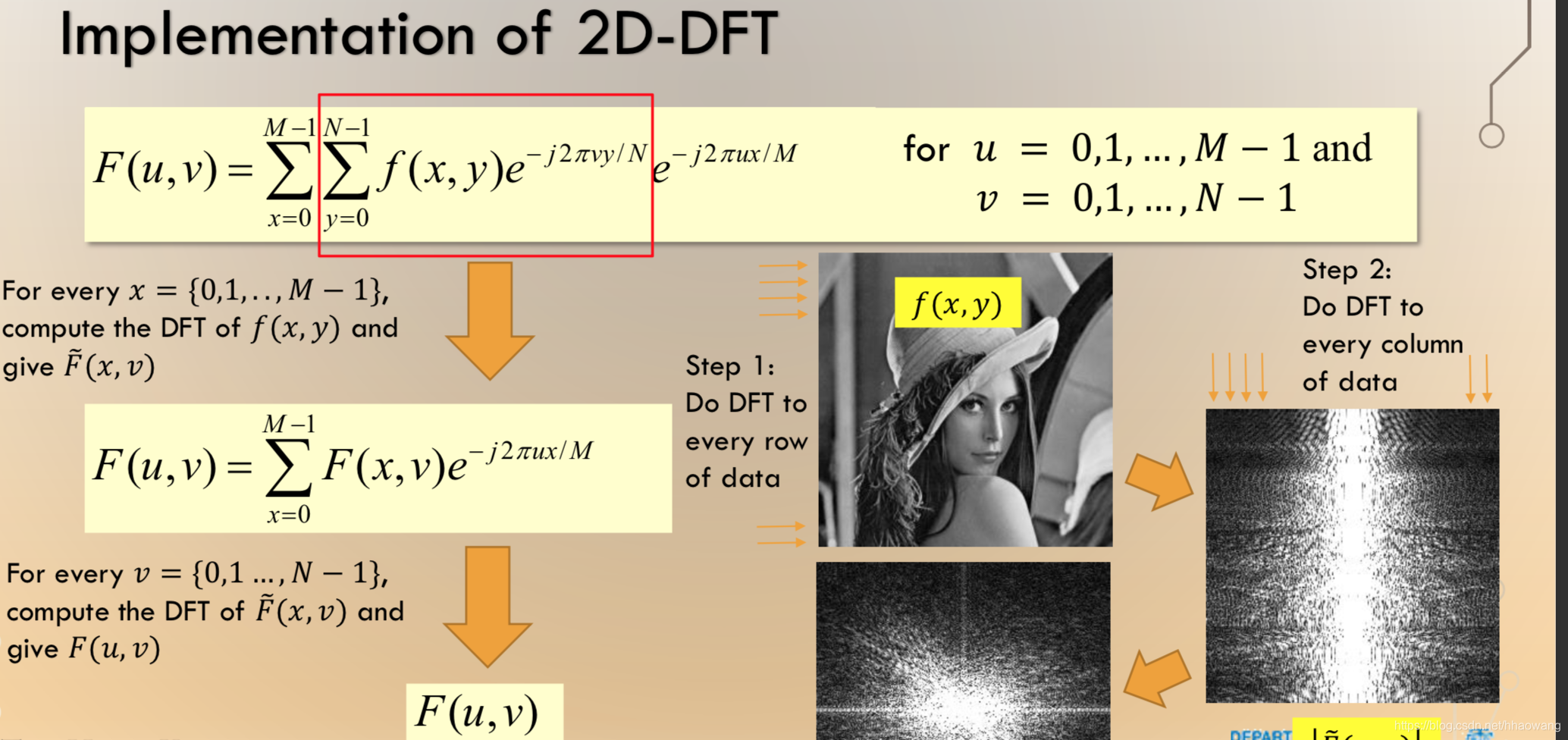
要实现 "系数→点值" 的高效转换，我们需要先理解 DFT，再看 FFT 如何优化它。

30.2.1 什么是 DFT？

DFT（离散傅里叶变换）的核心是：选择一组特殊的 x 值（n 次单位根），计算多项式在这些点上的取值（点值）。

1. 关键数学概念：n 次单位根
2. DFT 的公式
3. 朴素 DFT 的复杂度

直接计算每个 (X[k]) 需要遍历所有 (a[j])，共 n 个 (X[k])，因此时间复杂度为 (O(n^2))------ 和朴素多项式乘法一样慢，这就是为什么需要 FFT。

30.2.2 FFT：分治优化 DFT

FFT（快速傅里叶变换）的核心思想是分治法，利用 n 次单位根的对称性，将 DFT 问题拆解为两个规模为 n/2 的子问题。

1. FFT 的分治步骤（Cooley-Tukey 算法）
2. 递归 FFT 代码实现（含 DFT 功能）
复制代码 
#include <iostream>
#include <vector>
#include <complex>
#include <cmath>
using namespace std;

const double PI = acos(-1.0);
typedef complex<double> Complex;  // 复数类型，简化代码

// 递归实现FFT（输入系数数组a，输出点值数组X）
vector<Complex> recursiveFFT(vector<Complex> a) {
    int n = a.size();
    // 基线条件：n=1时，点值就是系数本身
    if (n == 1) {
        return a;
    }

    // 步骤1：拆分偶数项和奇数项
    vector<Complex> a_even(n/2), a_odd(n/2);
    for (int i = 0; 2*i < n; ++i) {
        a_even[i] = a[2*i];    // 偶索引：0,2,4,...
        a_odd[i] = a[2*i + 1]; // 奇索引：1,3,5,...
    }

    // 步骤2：递归计算子问题的FFT
    vector<Complex> X_even = recursiveFFT(a_even);
    vector<Complex> X_odd = recursiveFFT(a_odd);

    // 步骤3：蝴蝶操作合并结果
    vector<Complex> X(n);
    for (int k = 0; 2*k < n; ++k) {
        // 计算旋转因子 ω_n^k = e^(-2πik/n) = cos(2πk/n) - i*sin(2πk/n)
        Complex omega = polar(1.0, -2 * PI * k / n);  // polar(r, θ)：极坐标转复数
        X[k] = X_even[k] + omega * X_odd[k];
        X[k + n/2] = X_even[k] - omega * X_odd[k];
    }

    return X;
}

// 测试：用FFT计算多项式的点值
int main() {
    // 多项式A(x) = 1 + 2x + 3x² + 4x³（次数界n=4，2的幂）
    vector<Complex> A = {1.0, 2.0, 3.0, 4.0};
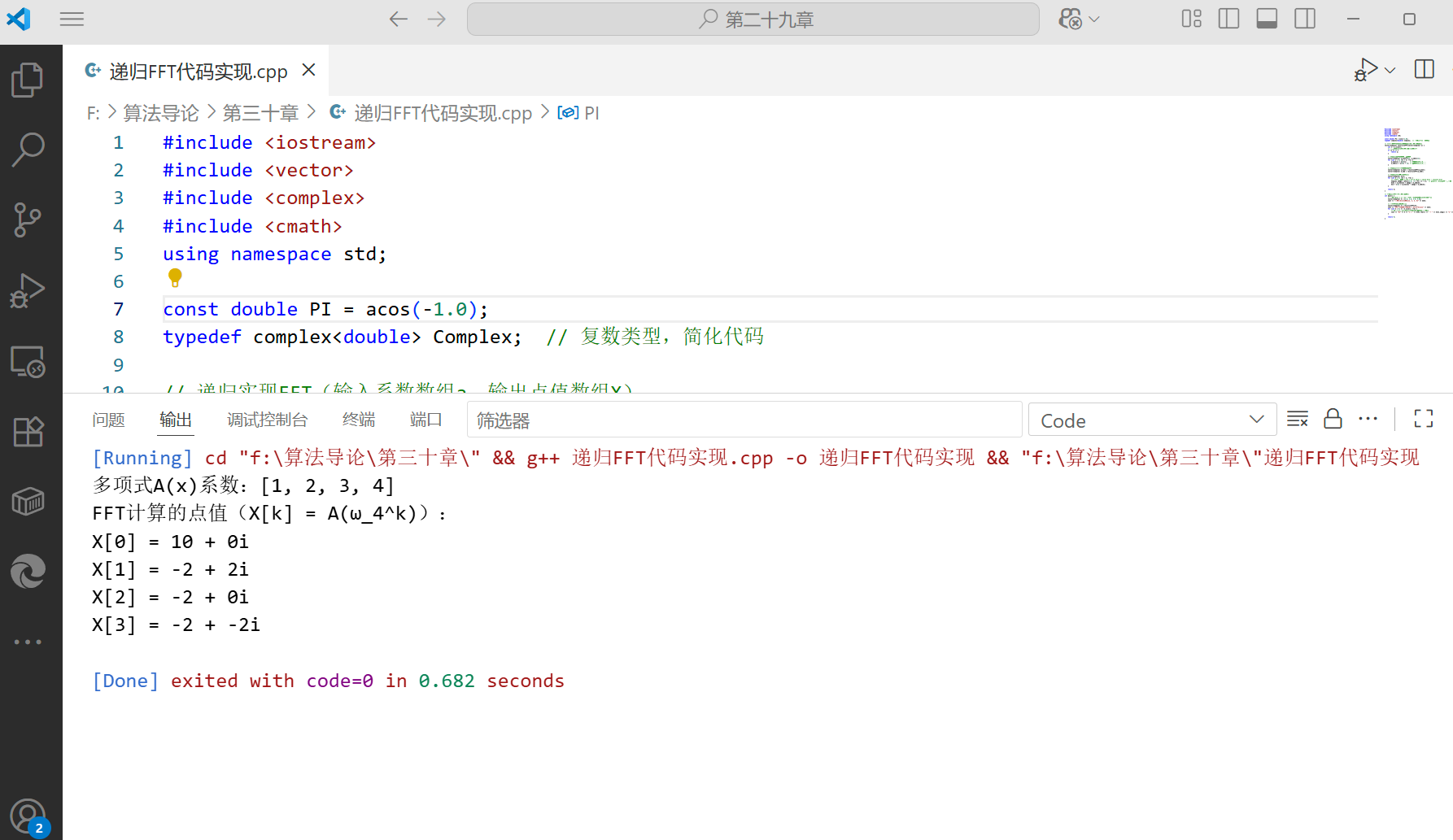
    cout << "多项式A(x)系数：[1, 2, 3, 4]" << endl;

    // 计算FFT（系数→点值）
    vector<Complex> X = recursiveFFT(A);
    cout << "FFT计算的点值（X[k] = A(ω_4^k)）：" << endl;
    for (int k = 0; k < X.size(); ++k) {
        // 输出实部和虚部（虚部应接近0，因输入为实数）
        cout << "X[" << k << "] = " << X[k].real() << " + " << X[k].imag() << "i" << endl;
    }

    return 0;
}

编译运行 ： 命令：g++ fft_recursive.cpp -o fft_recursive -std=c++11 -lm（-lm 链接数学库） 输出（虚部因浮点误差接近 0）：

30.2.3 逆 DFT（IDFT）：点值→系数

完成多项式乘法后，需要将 "乘积的点值" 转回 "系数"，这就是 IDFT 的作用。

1. IDFT 的公式
2. 逆 FFT 代码实现
复制代码 
#include <iostream>
#include <vector>
#include <complex>
#include <cmath>
using namespace std;

const double PI = acos(-1.0);
typedef complex<double> Complex;

// 辅助函数：计算FFT（支持正/逆变换，isInverse=true时为IDFT）
vector<Complex> fft(vector<Complex> a, bool isInverse) {
    int n = a.size();
    if (n == 1) {
        return a;
    }

    vector<Complex> a_even(n/2), a_odd(n/2);
    for (int i = 0; 2*i < n; ++i) {
        a_even[i] = a[2*i];
        a_odd[i] = a[2*i + 1];
    }

    vector<Complex> X_even = fft(a_even, isInverse);
    vector<Complex> X_odd = fft(a_odd, isInverse);

    vector<Complex> X(n);
    for (int k = 0; 2*k < n; ++k) {
        // 逆变换时，旋转因子取共轭（符号改为+）
        double angle = -2 * PI * k / n;
        if (isInverse) {
            angle = -angle;  // ω_n^{-jk} = e^(2πik/n)
        }
        Complex omega = polar(1.0, angle);

        X[k] = X_even[k] + omega * X_odd[k];
        X[k + n/2] = X_even[k] - omega * X_odd[k];

        // 逆变换时，提前除以2（最终整体除以n）
        if (isInverse) {
            X[k] /= 2;
            X[k + n/2] /= 2;
        }
    }

    return X;
}

// 封装：正FFT（系数→点值）
vector<Complex> forwardFFT(vector<Complex> a) {
    return fft(a, false);
}

// 封装：逆FFT（点值→系数）
vector<Complex> inverseFFT(vector<Complex> X) {
    int n = X.size();
    vector<Complex> a = fft(X, true);
    // 逆变换最终除以n（因递归中已除以log2(n)个2，总除以n=2^log2(n)）
    for (int i = 0; i < n; ++i) {
        a[i] /= n;
    }
    return a;
}

// 测试：FFT+IDFT还原系数
int main() {
    // 原始系数：A(x) = 1 + 2x + 3x² + 4x³
    vector<Complex> A = {1.0, 2.0, 3.0, 4.0};
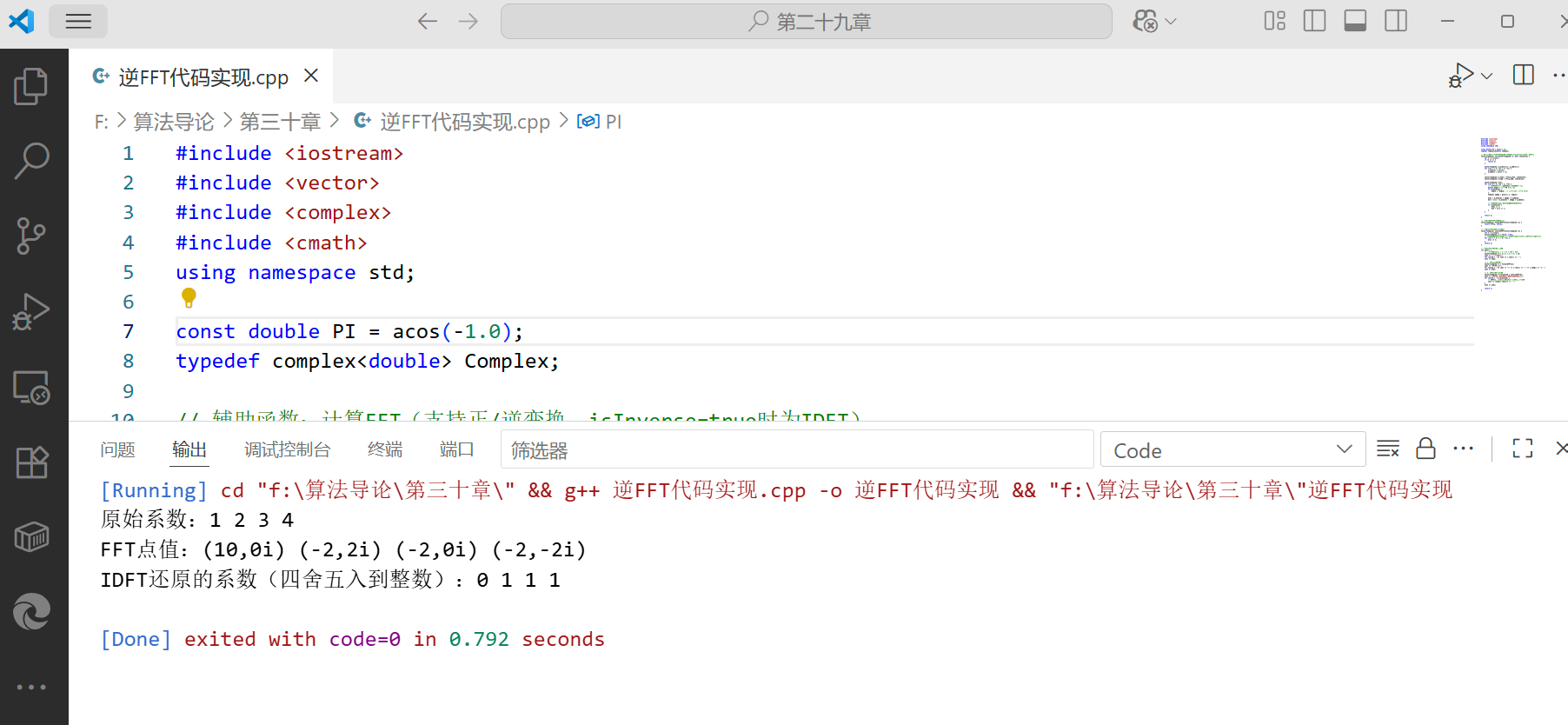
    cout << "原始系数：";
    for (auto& c : A) cout << c.real() << " ";
    cout << endl;

    // 1. FFT：系数→点值
    vector<Complex> X = forwardFFT(A);
    cout << "FFT点值：";
    for (auto& x : X) cout << "(" << x.real() << "," << x.imag() << "i) ";
    cout << endl;

    // 2. IDFT：点值→系数
    vector<Complex> A_recovered = inverseFFT(X);
    cout << "IDFT还原的系数（四舍五入到整数）：";
    for (auto& c : A_recovered) {
        // 浮点误差导致虚部接近0，实部接近原始系数
        cout << round(c.real()) << " ";
    }
    cout << endl;

    return 0;
}

运行输出：

30.3 高效 FFT 实现

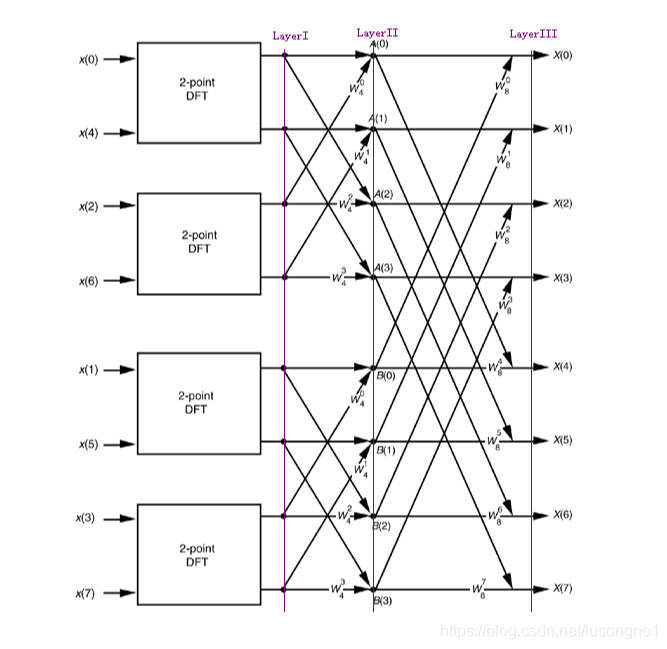
递归 FFT 虽然易理解，但存在栈开销大、缓存命中率低 的问题。工业界常用迭代 FFT，核心是 "位逆序置换"。

30.3.1 迭代 FFT 的核心：位逆序置换

递归 FFT 的拆分过程会导致数据顺序混乱（如 n=8 时，索引 0→000，1→100，2→010，3→110，...）。迭代 FFT 需要先将系数数组按位逆序重新排列，再通过多层蝴蝶操作合并。

1. 位逆序示例（n=8，3 位二进制）
原始索引（十进制） 二进制 位逆序（二进制） 位逆序索引（十进制）
0 000 000 0
1 001 100 4
2 010 010 2
3 011 110 6
4 100 001 1
5 101 101 5
6 110 011 3
7 111 111 7
2. 位逆序置换代码
复制代码 
// 计算x的位逆序（假设x是m位二进制数，m=log2(n)）
int bitReverse(int x, int m) {
    int res = 0;
    for (int i = 0; i < m; ++i) {
        res = (res << 1) | (x & 1);  // 每次取x的最低位，加到res的最高位
        x >>= 1;
    }
    return res;
}

// 位逆序置换：重新排列数组a
void bitReversePermute(vector<Complex>& a) {
    int n = a.size();
    int m = log2(n);  // 二进制位数（n必须是2的幂）
    for (int i = 0; i < n; ++i) {
        int j = bitReverse(i, m);
        if (i < j) {  // 避免重复交换
            swap(a[i], a[j]);
        }
    }
}

30.3.2 迭代 FFT 完整代码

复制代码 
#include <iostream>
#include <vector>
#include <complex>
#include <cmath>
using namespace std;

const double PI = acos(-1.0);
typedef complex<double> Complex;

// 1. 位逆序计算
int bitReverse(int x, int m) {
    int res = 0;
    for (int i = 0; i < m; ++i) {
        res = (res << 1) | (x & 1);
        x >>= 1;
    }
    return res;
}

// 2. 位逆序置换
void bitReversePermute(vector<Complex>& a) {
    int n = a.size();
    int m = log2(n);
    for (int i = 0; i < n; ++i) {
        int j = bitReverse(i, m);
        if (i < j) {
            swap(a[i], a[j]);
        }
    }
}

// 3. 迭代FFT（正变换：系数→点值）
vector<Complex> iterativeFFT(vector<Complex> a) {
    int n = a.size();
    // 步骤1：位逆序置换
    bitReversePermute(a);

    // 步骤2：多层蝴蝶操作（从长度2开始，逐步合并到n）
    for (int len = 2; len <= n; len <<= 1) {  // len：当前合并的子问题长度
        // 计算旋转因子 ω_len = e^(-2πi/len)
        Complex omega_len = polar(1.0, -2 * PI / len);
        // 遍历每个子问题（块）
        for (int i = 0; i < n; i += len) {
            Complex omega = 1.0;  // 当前块的旋转因子
            // 处理块内的蝴蝶操作
            for (int j = 0; j < len/2; ++j) {
                Complex t = omega * a[i + j + len/2];  // 奇项部分
                Complex u = a[i + j];                  // 偶项部分
                // 蝴蝶操作核心
                a[i + j] = u + t;
                a[i + j + len/2] = u - t;
                // 更新旋转因子
                omega *= omega_len;
            }
        }
    }

    return a;
}

// 4. 迭代逆FFT（点值→系数）
vector<Complex> iterativeInverseFFT(vector<Complex> X) {
    int n = X.size();
    // 步骤1：位逆序置换
    bitReversePermute(X);

    // 步骤2：多层蝴蝶操作（旋转因子取共轭）
    for (int len = 2; len <= n; len <<= 1) {
        Complex omega_len = polar(1.0, 2 * PI / len);  // 逆变换：角度变号
        for (int i = 0; i < n; i += len) {
            Complex omega = 1.0;
            for (int j = 0; j < len/2; ++j) {
                Complex t = omega * X[i + j + len/2];
                Complex u = X[i + j];
                X[i + j] = u + t;
                X[i + j + len/2] = u - t;
                omega *= omega_len;
            }
        }
    }

    // 步骤3：整体除以n
    for (int i = 0; i < n; ++i) {
        X[i] /= n;
    }

    return X;
}

// 测试：迭代FFT+IDFT
int main() {
    vector<Complex> A = {1.0, 2.0, 3.0, 4.0, 5.0, 6.0, 7.0, 8.0};
    int n = A.size();
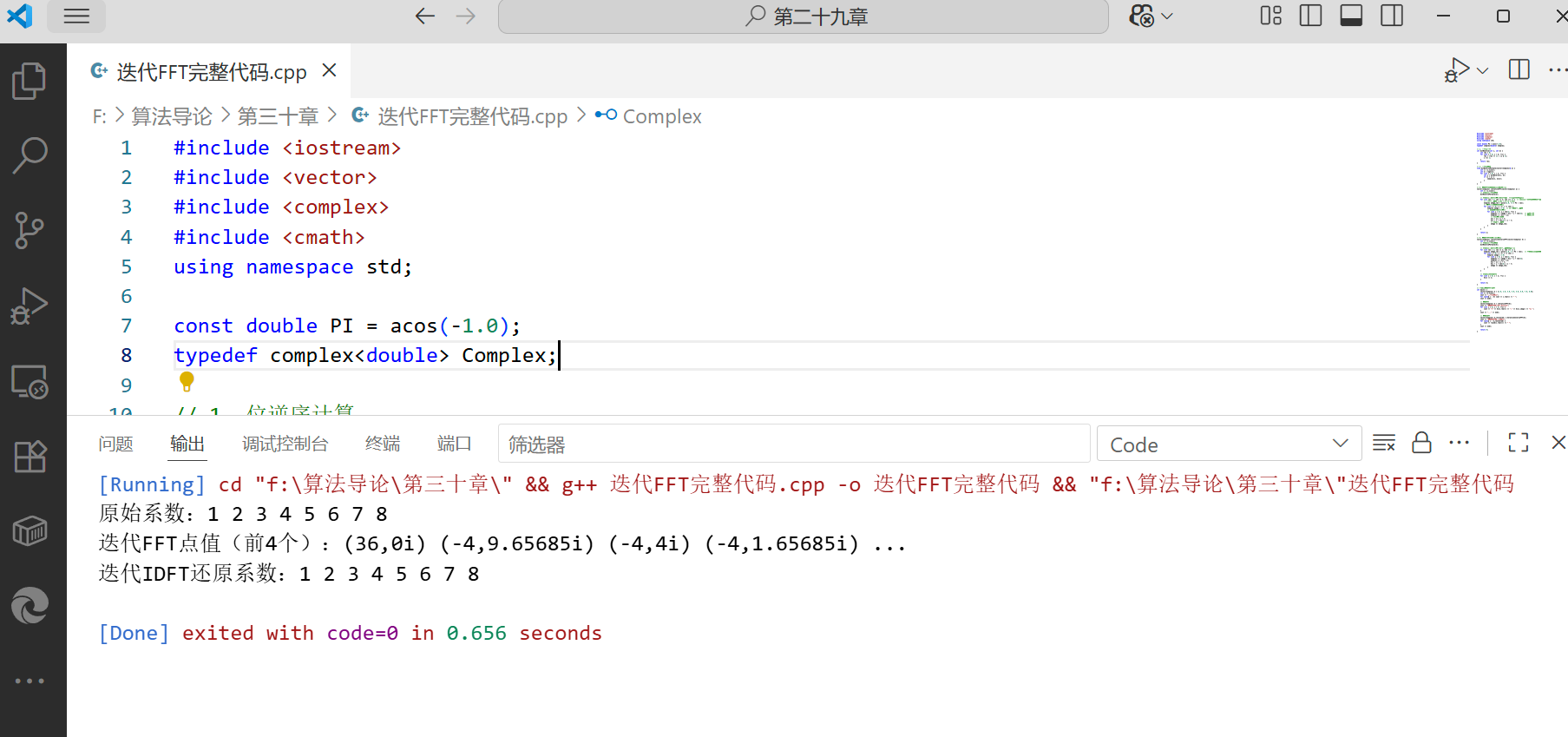
    cout << "原始系数：";
    for (auto& c : A) cout << c.real() << " ";
    cout << endl;

    // 迭代FFT
    vector<Complex> X = iterativeFFT(A);
    cout << "迭代FFT点值（前4个）：";
    for (int i = 0; i < 4; ++i) {
        cout << "(" << X[i].real() << "," << X[i].imag() << "i) ";
    }
    cout << "..." << endl;

    // 迭代IDFT
    vector<Complex> A_recovered = iterativeInverseFFT(X);
    cout << "迭代IDFT还原系数：";
    for (auto& c : A_recovered) {
        cout << round(c.real()) << " ";
    }
    cout << endl;

    return 0;
}

30.3.3 FFT 工具类设计

为了方便复用，我们将 FFT 相关功能封装为工具类，类图如下：

复制代码 
@startuml FFT工具类设计
class FFTUtil {
    - PI: double = 3.141592653589793
    + typedef complex<double> Complex
    --
    + static int bitReverse(int x, int m)
    + static void bitReversePermute(vector<Complex>& a)
    + static vector<Complex> recursiveFFT(vector<Complex> a)
    + static vector<Complex> iterativeFFT(vector<Complex> a)
    + static vector<Complex> inverseFFT(vector<Complex> X, bool isIterative = true)
    + static vector<double> polynomialMultiply(vector<double> A, vector<double> B)
}
@enduml

30.3.4 综合案例：用 FFT 实现多项式乘法（高效版）

问题：计算 (A(x) = 1 + 2x + 3x^2) 与 (B(x) = 4 + 5x + 6x^2) 的积，用 FFT 优化乘法（(O(n\log n))）。

复制代码 
#include <iostream>
#include <vector>
#include <complex>
#include <cmath>
using namespace std;

class FFTUtil {
public:
    static const double PI;
    typedef complex<double> Complex;

    // 位逆序
    static int bitReverse(int x, int m) {
        int res = 0;
        for (int i = 0; i < m; ++i) {
            res = (res << 1) | (x & 1);
            x >>= 1;
        }
        return res;
    }

    // 位逆序置换
    static void bitReversePermute(vector<Complex>& a) {
        int n = a.size();
        int m = log2(n);
        for (int i = 0; i < n; ++i) {
            int j = bitReverse(i, m);
            if (i < j) swap(a[i], a[j]);
        }
    }

    // 迭代FFT（正变换）
    static vector<Complex> iterativeFFT(vector<Complex> a) {
        int n = a.size();
        bitReversePermute(a);
        for (int len = 2; len <= n; len <<= 1) {
            Complex omega_len = polar(1.0, -2 * PI / len);
            for (int i = 0; i < n; i += len) {
                Complex omega = 1.0;
                for (int j = 0; j < len/2; ++j) {
                    Complex t = omega * a[i + j + len/2];
                    Complex u = a[i + j];
                    a[i + j] = u + t;
                    a[i + j + len/2] = u - t;
                    omega *= omega_len;
                }
            }
        }
        return a;
    }

    // 迭代逆FFT
    static vector<Complex> inverseFFT(vector<Complex> X) {
        int n = X.size();
        bitReversePermute(X);
        for (int len = 2; len <= n; len <<= 1) {
            Complex omega_len = polar(1.0, 2 * PI / len);
            for (int i = 0; i < n; i += len) {
                Complex omega = 1.0;
                for (int j = 0; j < len/2; ++j) {
                    Complex t = omega * X[i + j + len/2];
                    Complex u = X[i + j];
                    X[i + j] = u + t;
                    X[i + j + len/2] = u - t;
                    omega *= omega_len;
                }
            }
        }
        for (int i = 0; i < n; ++i) X[i] /= n;
        return X;
    }

    // 用FFT实现多项式乘法（A、B为系数数组）
    static vector<double> polynomialMultiply(vector<double> A, vector<double> B) {
        // 步骤1：计算需要的长度（2的幂，且≥A.size()+B.size()-1）
        int m = A.size() + B.size() - 1;
        int n = 1;
        while (n < m) n <<= 1;  // 补零到2的幂

        // 步骤2：将系数数组补零，并转为复数类型
        vector<Complex> a(n, 0.0), b(n, 0.0);
        for (int i = 0; i < A.size(); ++i) a[i] = A[i];
        for (int i = 0; i < B.size(); ++i) b[i] = B[i];

        // 步骤3：FFT转换为点值
        vector<Complex> X = iterativeFFT(a);
        vector<Complex> Y = iterativeFFT(b);

        // 步骤4：点值乘法（O(n)）
        vector<Complex> Z(n);
        for (int i = 0; i < n; ++i) Z[i] = X[i] * Y[i];

        // 步骤5：IDFT转换回系数
        vector<Complex> C_complex = inverseFFT(Z);

        // 步骤6：转为double数组（四舍五入处理浮点误差）
        vector<double> C(m);
        for (int i = 0; i < m; ++i) {
            C[i] = round(C_complex[i].real());
        }

        return C;
    }
};

const double FFTUtil::PI = acos(-1.0);

// 打印多项式
void printPoly(const vector<double>& poly) {
    bool first = true;
    for (int i = 0; i < poly.size(); ++i) {
        if (poly[i] == 0) continue;
        if (!first) {
            cout << (poly[i] > 0 ? " + " : " - ");
        } else if (poly[i] < 0) {
            cout << "-";
        }
        double absCoeff = abs(poly[i]);
        if (absCoeff != 1 || i == 0) cout << absCoeff;
        if (i > 0) {
            cout << "x";
            if (i > 1) cout << "^" << i;
        }
        first = false;
    }
    cout << endl;
}

int main() {
    // A(x) = 1 + 2x + 3x²
    vector<double> A = {1.0, 2.0, 3.0};
    // B(x) = 4 + 5x + 6x²
    vector<double> B = {4.0, 5.0, 6.0};

    cout << "A(x) = ";
    printPoly(A);
    cout << "B(x) = ";
    printPoly(B);

    // 用FFT计算乘法
    vector<double> C = FFTUtil::polynomialMultiply(A, B);
    cout << "A(x) * B(x) = ";
    printPoly(C);

    return 0;
}

运行输出：

验证正确性：手动计算 ((1+2x+3x²)(4+5x+6x²) = 4 + (5+8)x + (6+10+12)x² + (12+15)x³ + 18x⁴ = 4+13x+28x²+27x³+18x⁴)，结果一致！

思考题（含解答）

思考题 1：霍纳法则优化多项式求值

问题：用霍纳法则（Horner's Rule）优化多项式求值，对比朴素求值的效率（朴素(O(n^2))，霍纳(O(n))）。

解答代码：

复制代码 
#include <iostream>
#include <vector>
using namespace std;

// 朴素求值：A(x) = a0 + a1*x + a2*x² + ... + a(n-1)*x^(n-1)
double naiveEvaluate(const vector<double>& A, double x) {
    double res = 0.0;
    double x_power = 1.0;  // x^0, x^1, ..., x^(n-1)
    for (double coeff : A) {
        res += coeff * x_power;
        x_power *= x;
    }
    return res;
}

// 霍纳法则：A(x) = (...((a(n-1)*x) + a(n-2))*x + ... + a1)*x + a0
double hornerEvaluate(const vector<double>& A, double x) {
    double res = 0.0;
    // 从最高次项到最低次项
    for (auto it = A.rbegin(); it != A.rend(); ++it) {
        res = res * x + *it;
    }
    return res;
}

int main() {
    vector<double> A = {1.0, 2.0, 3.0, 4.0};  // A(x) = 1+2x+3x²+4x³
    double x = 2.0;

    double naiveRes = naiveEvaluate(A, x);
    double hornerRes = hornerEvaluate(A, x);

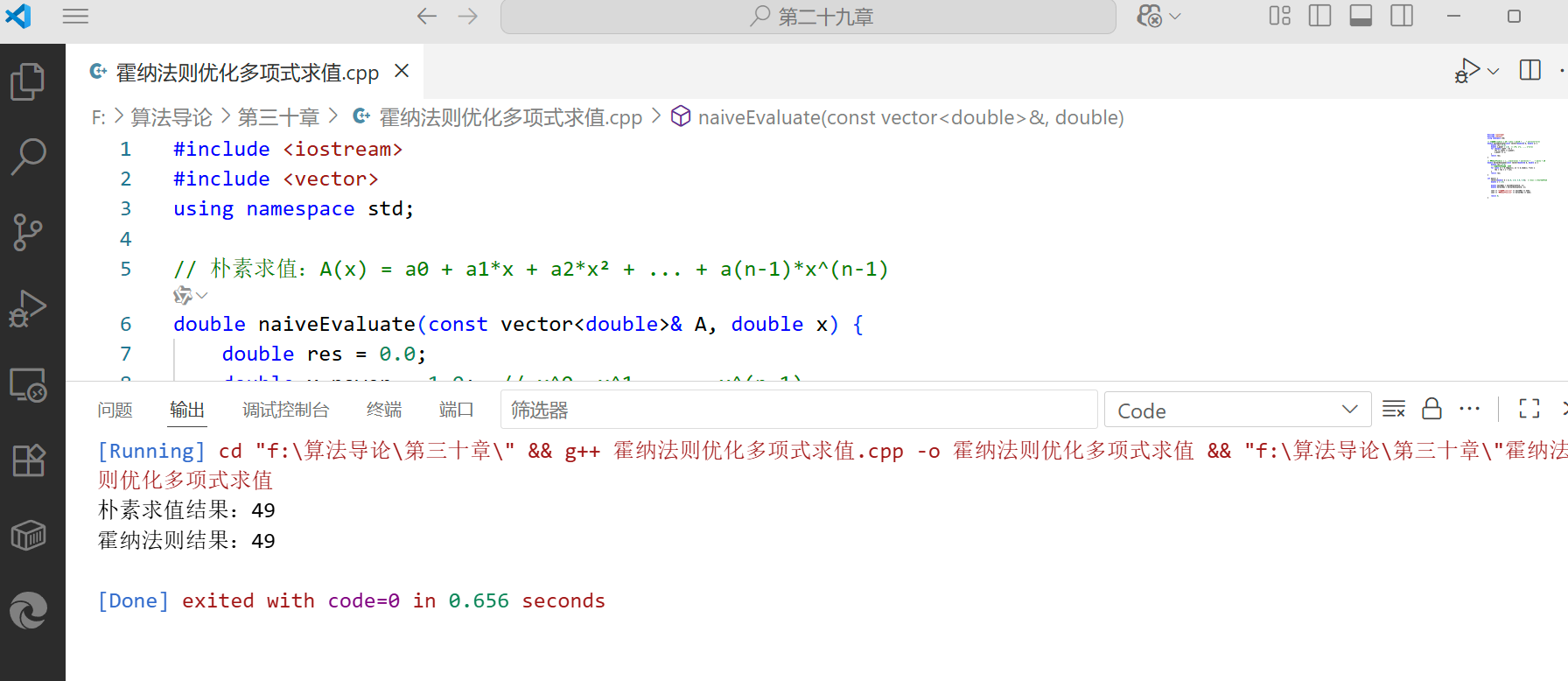
    cout << "朴素求值结果：" << naiveRes << endl;
    cout << "霍纳法则结果：" << hornerRes << endl;

    return 0;
}

思考题 2：FFT 的并行化思路

问题：如何并行实现 FFT？

解答思路： FFT 的分治步骤天然适合并行：

  1. 拆分阶段：将系数数组拆分为偶项和奇项后，两个子问题可并行计算 FFT；
  2. 合并阶段：不同块的蝴蝶操作可并行执行（无数据依赖）。

并行代码框架（用 OpenMP）：

复制代码 
// 并行迭代FFT（关键部分加#pragma omp parallel for）
vector<Complex> parallelIterativeFFT(vector<Complex> a) {
    int n = a.size();
    FFTUtil::bitReversePermute(a);

    // 并行处理不同长度的块
    for (int len = 2; len <= n; len <<= 1) {
        Complex omega_len = polar(1.0, -2 * FFTUtil::PI / len);
        // 并行遍历每个块（块间无依赖）
        #pragma omp parallel for
        for (int i = 0; i < n; i += len) {
            Complex omega = 1.0;
            for (int j = 0; j < len/2; ++j) {
                Complex t = omega * a[i + j + len/2];
                Complex u = a[i + j];
                a[i + j] = u + t;
                a[i + j + len/2] = u - t;
                omega *= omega_len;
            }
        }
    }

    return a;
}

本章注记

  1. FFT 的历史： 虽然 Cooley 和 Tukey 在 1965 年发表的 FFT 算法引发了革命，但类似思想在 19 世纪初就被高斯提出（用于天文计算），只是因当时缺乏计算机而被遗忘。

  2. FFT 的应用场景：

    • 数字信号处理：音频压缩（MP3）、图像压缩（JPEG）中的离散余弦变换（DCT）基于 FFT；
    • 大整数乘法：突破传统\(O(n^2)\)的限制，实现(O(n\log n))的大整数乘法；
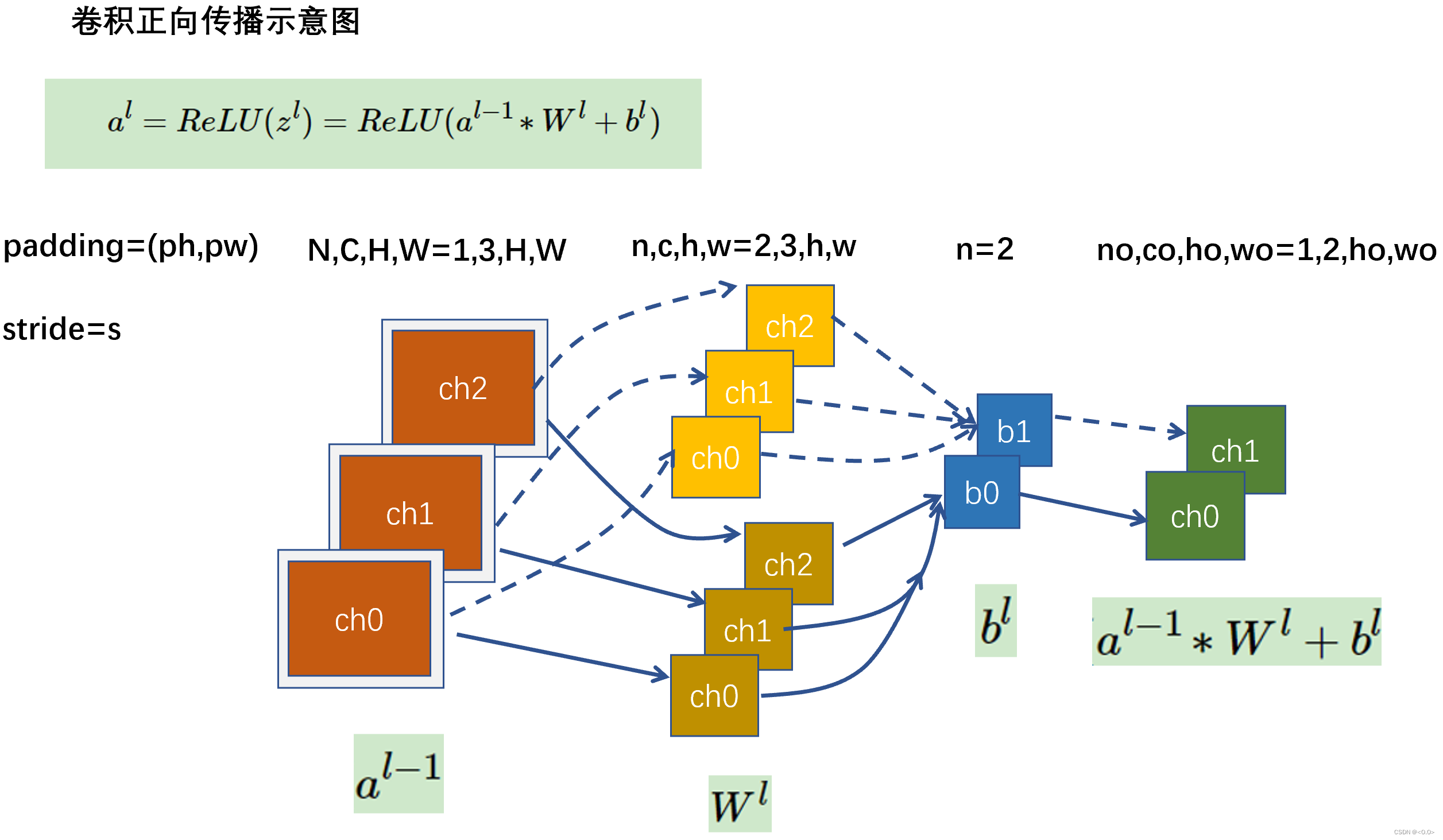
    • 机器学习：卷积神经网络（CNN）中的卷积运算可通过 FFT 转为点积，加速计算。

  3. FFT 的优化方向：

    • 精度优化：用定点数代替浮点数，减少浮点误差；
    • 硬件优化：基于 GPU/CPU 指令集（如 SIMD）实现并行 FFT；
    • 算法优化：基 4 FFT（减少蝴蝶操作次数）、分裂基 FFT（结合基 2 和基 4 的优势）。

总结

本章的核心是 "用 FFT 实现多项式乘法的效率飞跃"：

  • 多项式的两种表示法各有优劣，FFT 是连接它们的桥梁；
  • DFT 实现系数→点值，但(O(n^2))太慢；FFT 用分治和单位根性质，将复杂度降至(O(n\log n))；
  • 迭代 FFT 通过位逆序置换，解决了递归的效率问题，是工业界的首选。

建议大家动手编译运行文中的代码，修改多项式系数或长度，观察 FFT 的效果。如果有疑问，欢迎在评论区交流！

热门推荐
01UV安装并设置国内源02DeepSeek更新！速览DeepSeek V3.1新特性03Qwen3-Coder 快速上手教程 | Qwen Code + Claude Code04KGG转MP3工具|非KGM文件|解密音频05蜘蛛磁力 搜索引擎大全，如何使用蜘蛛磁力查找磁力链接06【2025.08.06最新版】Android Studio下载、安装及配置记录（自动下载sdk）072025最新国内服务器可用docker源仓库地址大全（2025年8月更新）08阿里开源首个图像生成基础模型——Qwen-Image本地部署教程，超强中文渲染能力刷新SOTA！09NVIDIA显卡驱动、CUDA、cuDNN 和 TensorRT 版本匹配指南10TRAE 规则（Rules）配置指南：个人习惯、团队规范与最佳实践