机器学习之数据模型训练（三）

荼蘼2025-08-20 14:10

目录

多种机器学习模型在分类任务中的对比实验

[一、详解网格搜索（Grid Search）调参：原理、实现与应用](#一、详解网格搜索（Grid Search）调参：原理、实现与应用)

[1. 什么是网格搜索？](#1. 什么是网格搜索？)

[2. 核心思想](#2. 核心思想)

[3. 与交叉验证的结合](#3. 与交叉验证的结合)

二、多种分类模型对比

[1. 逻辑斯蒂回归（Logistic Regression）](#1. 逻辑斯蒂回归（Logistic Regression）)

[1. 参数网格搜索（Grid Search）调优](#1. 参数网格搜索（Grid Search）调优)

[2. 使用最优参数构建模型](#2. 使用最优参数构建模型)

[3. 模型预测与评估](#3. 模型预测与评估)

[2. 随机森林（Random Forest）](#2. 随机森林（Random Forest）)

[3. 支持向量机（SVM）](#3. 支持向量机（SVM）)

[4. XGBoost](#4. XGBoost)

[5. 高斯朴素贝叶斯（Gaussian Naive Bayes）](#5. 高斯朴素贝叶斯（Gaussian Naive Bayes）)

[6. AdaBoost](#6. AdaBoost)

三、结果分析

接上篇我们完成了数据的预处理，将文本转化为了模型可以训练的标准文本。本文我们将进行几种模型的训练，看看哪个模型的效果更明显。

多种机器学习模型在分类任务中的对比实验

在机器学习分类任务中，选择合适的模型往往是提升性能的关键。本文将使用逻辑斯蒂回归、随机森林、支持向量机、XGBoost、高斯朴素贝叶斯和 AdaBoost 六种经典模型，基于同一数据集进行分类实验，并对比各模型的表现。

一、详解网格搜索（Grid Search）调参：原理、实现与应用

1. 什么是网格搜索？

网格搜索是一种穷举式的超参数优化方法。它将每个超参数的可能取值视为一个维度，所有维度的组合构成一个 "参数网格"，然后在这个网格中逐个尝试所有可能的参数组合，通过交叉验证（Cross Validation）评估每个组合的性能，最终选择性能最优的参数组合。

2. 核心思想

  • 把超参数的可能取值用 "网格" 形式列出来（例如：C=[0.1,1,10]，penalty=['l1','l2']）；
  • 遍历网格中的每一个参数组合，训练模型并评估性能；
  • 保留性能最优的参数组合作为最终结果。

3. 与交叉验证的结合

网格搜索通常与交叉验证（如 K 折交叉验证）结合使用，原因是：

二、多种分类模型对比

  • 单一训练集的评估结果可能受数据划分影响，存在随机性；
  • 交叉验证通过多次划分训练集和验证集，取平均性能作为参数组合的评分，结果更稳健。

1. 逻辑斯蒂回归（Logistic Regression）

逻辑斯蒂回归是一种经典的线性分类模型，适用于二分类或多分类任务。

python 复制代码 
# 以下为参数调优过程（已注释）
# param_grid = [
#     {
#         'solver': ['newton-cg', 'lbfgs', 'sag'],
#         'penalty': ['l2', 'none'],
#         'C': [0.01, 0.1, 1, 10, 100],
#         'max_iter': [100, 200, 300],
#         'multi_class': ['auto', 'ovr', 'multinomial']
#     },
#     {
#         'solver': ['saga'],
#         'penalty': ['l1', 'l2', 'elasticnet', 'none'],
#         'C': [0.01, 0.1, 1, 10, 100],
#         'max_iter': [100, 200, 300],
#         'multi_class': ['auto', 'ovr', 'multinomial'],
#         'l1_ratio': [0.1, 0.5, 0.9]
#     }
# ]
# lr = LogisticRegression()
# grid_search = GridSearchCV(lr, param_grid, cv=5)
# grid_search.fit(train_data_x, train_data_y)
# print('最好的模型参数：')
# print(grid_search.best_params_)

# 使用最优参数构建模型
lr = LogisticRegression(C=0.01, max_iter=300, multi_class='auto', penalty='none', solver='lbfgs')
lr.fit(train_data_x, train_data_y)

# 预测与评估
pred = lr.predict(test_data_x)
pred1 = lr.predict(train_data_x)
print('逻辑斯蒂回归测试分类报告结果')
print(metrics.classification_report(test_data_y, pred))
print('逻辑斯蒂回归自测分类结果')
print(metrics.classification_report(train_data_y, pred1))

1. 参数网格搜索（Grid Search）调优

python 复制代码 
# 定义参数网格，包含不同求解器对应的参数组合
param_grid = [
    {
        # 第一组：适用于newton-cg、lbfgs、sag求解器的参数
        'solver': ['newton-cg', 'lbfgs', 'sag'],  # 优化求解器
        'penalty': ['l2', 'none'],  # 正则化方式（这些求解器不支持l1）
        'C': [0.01, 0.1, 1, 10, 100],  # 正则化强度的倒数（值越小正则化越强）
        'max_iter': [100, 200, 300],  # 最大迭代次数
        'multi_class': ['auto', 'ovr', 'multinomial']  # 多分类策略
    },
    {
        # 第二组：适用于saga求解器的参数（支持更多正则化方式）
        'solver': ['saga'],
        'penalty': ['l1', 'l2', 'elasticnet', 'none'],  # saga支持弹性网络等正则化
        'C': [0.01, 0.1, 1, 10, 100],
        'max_iter': [100, 200, 300],
        'multi_class': ['auto', 'ovr', 'multinomial'],
        'l1_ratio': [0.1, 0.5, 0.9]  # elasticnet专用参数（l1正则化比例）
    }
]

# 初始化逻辑回归模型
lr = LogisticRegression()

# 网格搜索：用5折交叉验证（cv=5）遍历所有参数组合
grid_search = GridSearchCV(lr, param_grid, cv=5)
grid_search.fit(train_data_x, train_data_y)  # 在训练数据上拟合

# 输出最优参数组合
print('最好的模型参数：')
print(grid_search.best_params_)

核心作用 ：

通过暴力搜索的方式，从参数网格中找到使模型在交叉验证中性能最优的参数组合，避免人工调参的主观性。

2. 使用最优参数构建模型

python 复制代码 
# 用最优参数实例化逻辑回归模型（这里展示的是搜索得到的一组最优参数）
lr = LogisticRegression(
    C=0.01,          # 正则化强度倒数（较小值表示较强正则化）
    max_iter=300,    # 最大迭代次数（确保模型收敛）
    multi_class='auto',  # 自动选择多分类策略
    penalty='none',  # 不使用正则化
    solver='lbfgs'   # 优化求解器
)

# 在训练数据上拟合模型
lr.fit(train_data_x, train_data_y)

核心作用 ：

基于最优参数配置，在完整训练集上重新训练模型，为后续预测做准备。

3. 模型预测与评估

使用训练好的模型在测试集和训练集上进行预测，并通过分类报告评估性能：

python 复制代码 
# 在测试集和训练集上进行预测
pred = lr.predict(test_data_x)    # 测试集预测结果
pred1 = lr.predict(train_data_x)  # 训练集预测结果

# 输出测试集分类报告（包含精确率、召回率、F1分数等）
print('逻辑斯蒂回归测试分类报告结果')
print(metrics.classification_report(test_data_y, pred))

# 输出训练集分类报告（用于判断是否过拟合）
print('逻辑斯蒂回归自测分类结果')
print(metrics.classification_report(train_data_y, pred1))

核心作用：

  • 测试集评估：判断模型的泛化能力（在新数据上的表现）。
  • 训练集评估：与测试集对比，若差距过大，可能存在过拟合或欠拟合问题。

经过训练该模型的报告如下：

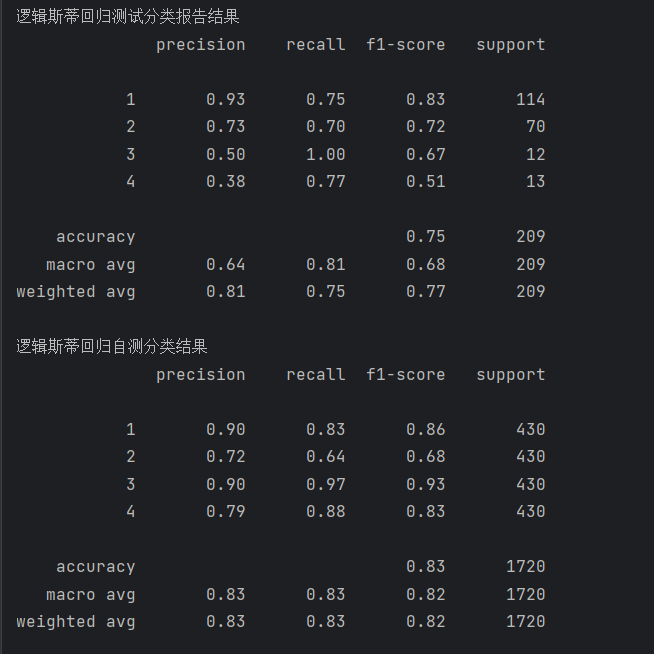
2. 随机森林（Random Forest）

随机森林是一种集成学习模型，由多个决策树组成，具有较强的泛化能力。

python 复制代码 
# 以下为参数调优过程（已注释）
# param_grid = {
#          'n_estimators': [100,200,300,400,500],
#          'max_depth': [5,10,15,20,25],
#         'min_samples_split':[2,5,10,20,50],
#         'min_samples_leaf':[1,2,5,10]}
# rf = RandomForestClassifier()
# grid_search = GridSearchCV(rf, param_grid, cv=5)
# grid_search.fit(train_data_x, train_data_y)
# print('最好的模型参数：')
# print(grid_search.best_params_)

# 使用最优参数构建模型
rf = RandomForestClassifier(max_depth=15, min_samples_leaf=1, min_samples_split=10, n_estimators=300)
rf.fit(train_data_x, train_data_y)

# 预测与评估
pred = rf.predict(train_data_x)
pred1 = rf.predict(test_data_x)
print('随机森林自测分类结果')
print(metrics.classification_report(train_data_y, pred))
print('随机森林测试分类结果')
print(metrics.classification_report(test_data_y, pred1))

该模型的结果如下：

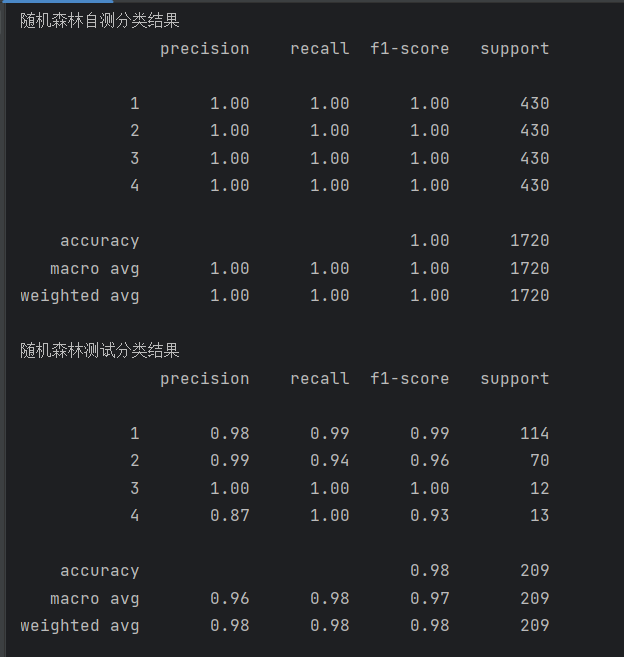
3. 支持向量机（SVM）

支持向量机通过寻找最优超平面来进行分类，在高维空间中表现出色。

python 复制代码 
# 构建SVM模型
svc = SVC(C=1, kernel='sigmoid', gamma='auto')
svc.fit(train_data_x, train_data_y)

# 预测与评估
pred = svc.predict(train_data_x)
pred1 = svc.predict(test_data_x)
print('支持向量机自测分类结果')
print(metrics.classification_report(train_data_y, pred))
print('支持向量机测试结果')
print(metrics.classification_report(test_data_y, pred1))

该模型的结果如下：

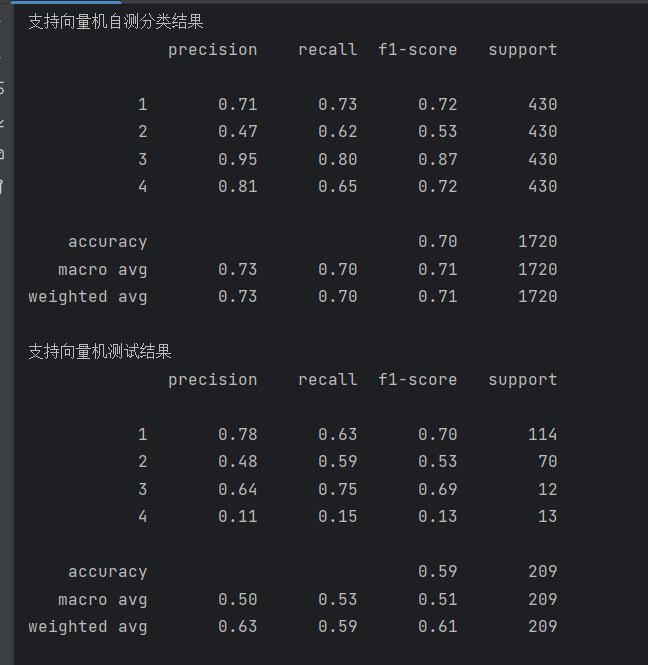
4. XGBoost

XGBoost 是一种高效的梯度提升树模型，在各类竞赛中常取得优异成绩。

python 复制代码 
# 构建XGBoost模型（需要对标签进行编码）
xgb = XGBClassifier(n_estimators=100, max_depth=3, learning_rate=0.1)
le = LabelEncoder()
train_data_y_encoded = le.fit_transform(train_data_y)
test_data_y_encoded = le.transform(test_data_y)
xgb.fit(train_data_x, train_data_y_encoded)

# 预测与评估（需将预测结果解码）
pred_test_encoded = xgb.predict(test_data_x)
pred_train_encoded = xgb.predict(train_data_x)
pred1 = le.inverse_transform(pred_test_encoded)
pred = le.inverse_transform(pred_train_encoded)
print('XGBoost自测分类结果')
print(metrics.classification_report(train_data_y, pred))
print('XGBoost测试分类结果')
print(metrics.classification_report(test_data_y, pred1))

运行结果如下：

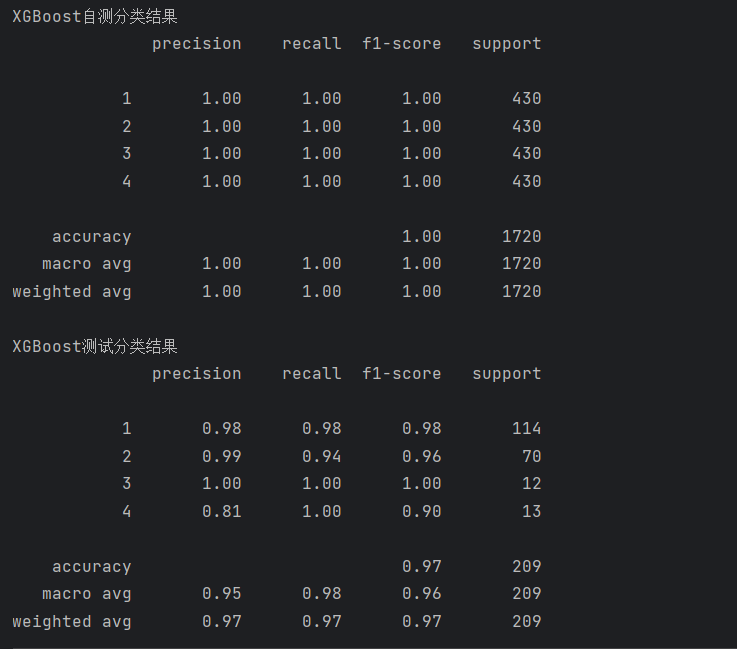
5. 高斯朴素贝叶斯（Gaussian Naive Bayes）

高斯朴素贝叶斯基于贝叶斯定理和特征条件独立假设，计算简单高效。

python 复制代码 
# 以下为参数调优过程（已注释）
# param_grid = {
#          'var_smoothing': [1e-12,1e-11,1e-10,1e-9],
#          'priors': [[0.2,0.2,0.3,0.3]]}
# gs = GaussianNB()
# grid_search = GridSearchCV(gs, param_grid, cv=5)
# grid_search.fit(train_data_x, train_data_y)
# print('最好的模型参数：')
# print(grid_search.best_params_)

# 使用最优参数构建模型
gs = GaussianNB(var_smoothing=1e-12)
gs.fit(train_data_x, train_data_y)

# 预测与评估
pred = gs.predict(train_data_x)
pred1 = gs.predict(test_data_x)
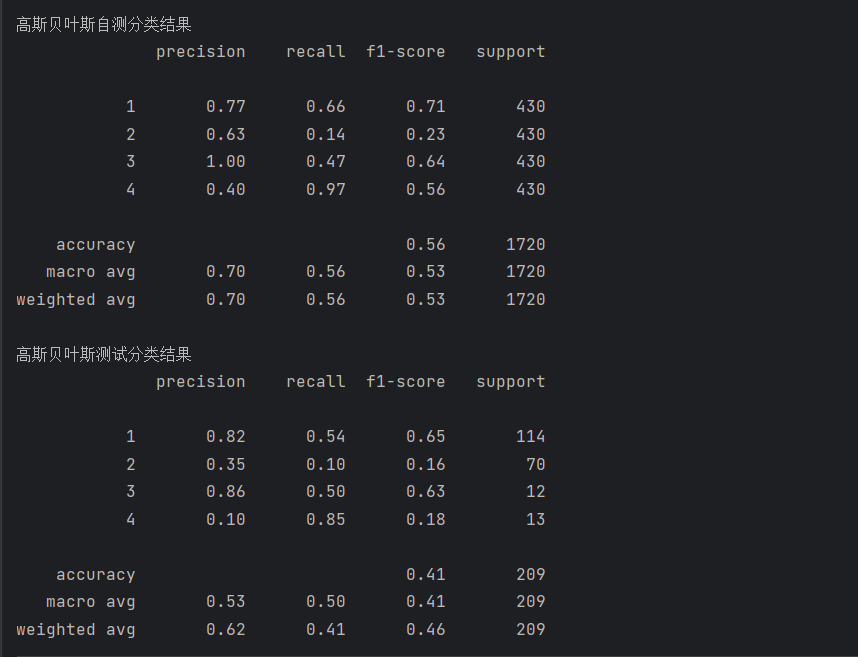
print('高斯贝叶斯自测分类结果')
print(metrics.classification_report(train_data_y, pred))
print('高斯贝叶斯测试分类结果')
print(metrics.classification_report(test_data_y, pred1))

运行结果如下：

6. AdaBoost

AdaBoost 是一种迭代式的集成学习算法，通过不断调整样本权重来训练弱分类器。

python 复制代码 
# 构建AdaBoost模型
ada = AdaBoostClassifier()
ada.fit(train_data_x, train_data_y)

# 预测与评估
pred = ada.predict(train_data_x)
pred1 = ada.predict(test_data_x)
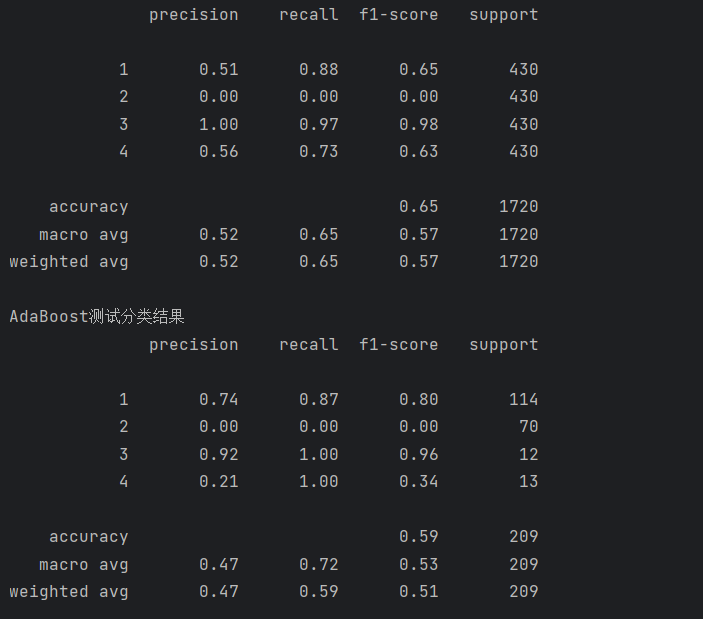
print('AdaBoost自测分类结果')
print(metrics.classification_report(train_data_y, pred))
print('AdaBoost测试分类结果')
print(metrics.classification_report(test_data_y, pred1))

运行结果如下：

三、结果分析

分类报告中包含了精确率（precision）、召回率（recall）、F1 分数（f1-score）和支持数（support）等指标：

  • 精确率：预测为正的样本中实际为正的比例
  • 召回率：实际为正的样本中被正确预测的比例
  • F1 分数：精确率和召回率的调和平均数，综合反映模型性能
  • 支持数：该类别的实际样本数量

根据上述运行结果可以看出使用随机森林模型的效果最好

热门推荐
01UV安装并设置国内源02DeepSeek更新！速览DeepSeek V3.1新特性03Qwen3-Coder 快速上手教程 | Qwen Code + Claude Code04KGG转MP3工具|非KGM文件|解密音频05蜘蛛磁力 搜索引擎大全，如何使用蜘蛛磁力查找磁力链接06【2025.08.06最新版】Android Studio下载、安装及配置记录（自动下载sdk）072025最新国内服务器可用docker源仓库地址大全（2025年8月更新）08阿里开源首个图像生成基础模型——Qwen-Image本地部署教程，超强中文渲染能力刷新SOTA！09NVIDIA显卡驱动、CUDA、cuDNN 和 TensorRT 版本匹配指南10Spring 调试终于不再痛苦了