机器学习概念(面试题库)

问题1：机器学习的基本分类有哪些？监督学习、无监督学习、半监督学习与强化学习有何区别。

机器学习的基本分类主要有 监督学习、无监督学习、半监督学习和强化学习 。它们的区别可以从 是否有标注数据、学习目标、训练方式 三个角度理解：

1. 监督学习（Supervised Learning）

- **数据特点**：训练数据包含输入 $X$ 和对应的**输出标签 $Y$**。
    
- **目标**：学习一个映射函数 $f:X→Y$，使得预测值尽可能接近真实标签。
    
- **典型任务**：分类（如垃圾邮件识别）、回归（如房价预测）。
    
- **核心思想**：通过大量"输入-输出"示例来学习规律。

2. 无监督学习（Unsupervised Learning）

- **数据特点**：只有输入数据 $X$，没有标签 $Y$。
    
- **目标**：发现数据内部的结构或模式。
    
- **典型任务**：聚类（如用户分群）、降维（如主成分分析 PCA）。
    
- **核心思想**：通过**数据自身的相似性或分布规律来理解结构**，而不依赖标签。

3. 半监督学习（Semi-supervised Learning）

- **数据特点**：数据中只有一小部分有标签，大部分是无标签的。
    
- **目标**：利用少量标注数据与大量未标注数据共同训练，提升学习效果。
    
- **典型任务**：网页分类、医学影像分析（标注代价高）。
    
- **核心思想**：通过**未标注数据的分布特性来辅助标注数据**，从而提高模型泛化能力。

4. 强化学习（Reinforcement Learning, RL）

- **数据特点**：**没有明确的输入-输出对，学习来自与环境交互**。
    
- **目标**：通过试错获得策略 π(a∣s)\pi(a|s)，使得长期累积奖励最大化。
    
- **典型任务**：自动驾驶、游戏 AI（AlphaGo）、机器人控制。
    
- **核心思想**：智能体在环境中基于"**奖励反馈**"学习如何做决策。

一句话概括：监督学习依赖标注，学输入到输出的函数；无监督学习没有标注，学数据内部规律；半监督学习用少量标注+大量未标注来优化模型；强化学习通过奖励机制与环境交互学最优策略。

问题2：什么是过拟合和欠拟合？你会如何解决过拟合

1. 欠拟合（Underfitting）

• 定义：模型太简单，无法捕捉数据的潜在规律，在训练集和测试集上表现都不好。

• 表现：训练误差高，测试误差也高。

• 例子：用线性模型去拟合高度非线性的数据。

2. 过拟合（Overfitting）

• 定义：模型过于复杂，把训练数据中的噪声或偶然规律也学到了，导致泛化能力差。

• 表现：训练误差很低，但测试误差很高。

• 例子：深度神经网络在小数据集上训练，几乎"记住"了所有训练样本，但对新样本预测差。

3. 解决过拟合的常见方法

• 数据层面

  • 增加训练数据（采集更多样本或用数据增强 techniques，如图像旋转、翻转）。

  • 降低噪声（清洗异常数据）。

• 模型层面

  • 降低模型复杂度（减少参数数量、降低网络深度或宽度）。

  • 使用正则化（L1/L2 正则项约束参数，防止过大权重）。

  • 使用 Dropout（在训练时随机丢弃部分神经元，防止依赖过强）。

  • 提前停止（Early Stopping：当验证误差开始上升时就停止训练）。

• 训练策略层面

  • 交叉验证（Cross Validation，帮助选择合适模型和参数）。

  • 使用集成学习（Bagging、Boosting，如随机森林、XGBoost），通过多个模型投票降低单模型过拟合风险。

一句话总结：欠拟合是学得不够，过拟合是学得太过；解决过拟合的核心思想是"更多数据 + 降低复杂度 + 正则化约束"。

问题3：**偏差-方差权衡（Bias-Variance Tradeoff）

1. 概念解释

• 偏差（Bias） ：指模型预测与真实结果之间的系统性误差，反映模型的"拟合能力"。

  • 偏差高 → 模型过于简单，难以捕捉真实规律 → 欠拟合。

• 方差（Variance） ：指模型对训练数据的敏感程度，反映模型的"稳定性"。

  • 方差高 → 模型过度依赖训练集，泛化能力差 → 过拟合。

误差可以分解为：

总误差=偏差2+方差+不可约误差总误差=偏差^2+方差+不可约误差总误差=偏差2+方差+不可约误差

其中，不可约误差来自数据中的噪声，无法通过建模消除。

2. 权衡关系

• 简单模型（如线性回归）：偏差大，方差小 → 倾向欠拟合。

• 复杂模型（如深度神经网络）：偏差小，方差大 → 倾向过拟合。

• 理想状态：找到既能降低偏差、又不过度增加方差的"平衡点"。

3. 应对方法

• 通过调整 模型复杂度 来平衡：

  • 偏差高时 → 增加模型复杂度（如增加特征、多层网络）。

  • 方差高时 → 使用正则化、集成方法或增加数据量。

• 使用 交叉验证 来选择合适的模型及参数，使其在验证集上达到最优平衡。

一句话总结：偏差-方差权衡就是在"欠拟合"（高偏差）和"过拟合"（高方差）之间找到最佳平衡，使模型既能学到数据规律，又能在新数据上表现良好。

问题4：常见的数据预处理和特征工程方法有哪些？如归一化、标准化、独热编码、处理缺失值等。

1. 数值型特征处理

• 归一化（Normalization）

  • 将数据缩放到固定区间（通常是 [0,1]）。

  • 公式：x =x−min⁡(x)max⁡(x)−min⁡(x)。x~= \frac{x - \min(x)}{\max(x)-\min(x)}。x =max(x)−min(x)x−min(x)。

  • 应用：对距离敏感的算法（如 KNN、SVM、神经网络）。

• 标准化（Standardization / Z-score）

  • 将数据转化为均值为 0、方差为 1 的分布。

  • 公式：xˉ=x−μσ。\bar{x}=\frac{x - \mu}{\sigma}。xˉ=σx−μ。

  • 应用：线性回归、逻辑回归、PCA 等假设数据服从正态分布的模型。

• 离群值处理

  • 方法：截断（clip）、替换（如用分位数）、或删除。

  • 避免极端值影响模型。

2. 类别型特征处理

• 独热编码（One-hot Encoding）

  • 将类别变量转化为稀疏的 0/1 向量。

  • 例：颜色 {红, 蓝, 绿} → [1,0,0], [0,1,0], [0,0,1]。

• 标签编码（Label Encoding）

  • 将类别变量转化为整数标签。

  • 缺点：可能引入虚假的数值大小关系。

• 目标编码（Target Encoding）

  • 用类别对应的目标值统计特征（如均值）替代类别。

  • 常用于高基数类别（如邮编、用户 ID）。

举例说明

标签编码（Label Encoding）

• 做法：给每个类别随便分配一个整数标签。
• 例子 ：
  • 北京 → 0
  • 上海 → 1
  • 广州 → 2
• 特点 ：
  • "0/1/2" 本身并没有真实数值含义，只是一个"代号"。
  • 但是如果你用线性模型或 KNN，模型会误以为有大小和距离关系（比如"上海=1"比"北京=0"大一点点，好像"上海>北京"）。
  • 在树模型（决策树、随机森林、XGBoost）中没问题，因为它们只会问"是否=某个类别"，不会利用数值大小。

目标编码（Target Encoding）

• 做法：用该类别在训练数据中对应的目标值（标签）的统计量来编码。
• 例子 （目标是"月消费额"）：
  • 北京：平均消费 = (3000+4000)/2 = 3500
  • 上海：平均消费 = 5000
  • 广州：平均消费 = 2000
• 特点 ：
  • 这里"编码值"是真实和任务相关的数值，反映了类别与目标变量的关系。
  • 好处：能把"类别"变成一个与预测目标有直接关系的数值。
  • 风险：如果直接在全数据集上计算，会"偷看答案"（数据泄漏）。所以通常要用交叉验证方式，在训练集分折后计算编码，再应用到验证集。

核心区别

• 标签编码：类别 → 任意整数代号（只表示身份，不含业务含义）。

• 目标编码：类别 → 与预测目标的统计值（含有业务信息，直接和任务相关）。

3. 缺失值处理

• 删除法：若缺失值比例极低，可删除相应样本或特征。

• 填补法：

  • 均值、中位数、众数填充。

  • 插值（如时间序列用前值填补）。

  • 模型预测填补（如 KNN、回归）。

4. 特征构造与选择

• 特征构造

  • 多项式特征（如x2,x⋅yx2,x⋅y如 x^2,x⋅yx^2, x \cdot y如x2,x⋅yx2,x⋅y）。

  • 特征交叉（如用户年龄 × 消费类别）。

  • 时间特征提取（如日期 → 年/月/周/节假日）。

• 特征选择

  • 过滤法（Filter）：基于统计指标（如方差阈值、卡方检验、相关系数）。

  • 包装法（Wrapper）：递归特征消除（RFE）。

  • 嵌入法（Embedded）：利用模型（如 Lasso、树模型的特征重要性）。

5. 其他常见方法

• 降维

  • PCA（主成分分析）：线性降维。

  • t-SNE / UMAP：非线性降维，常用于可视化。

• 数据增强（Data Augmentation）

  • 图像：旋转、平移、裁剪、加噪声。

  • 文本：同义词替换、随机删除。

数据预处理解决"数据质量"问题（归一化、标准化、缺失值、编码），特征工程解决"数据表达"问题（构造、选择、降维）。

问题5：降维方法有哪些？请简述 PCA、LDA 的原理及应用场景。

1️.常见的降维方法

• 线性降维

  • PCA（主成分分析）

  • LDA（线性判别分析）

  • ICA（独立成分分析）

• 非线性降维（流形学习）

  • t-SNE（t 分布随机邻居嵌入）

  • UMAP（统一流形近似与投影）

  • ISOMAP（等距映射）

2️ .PCA（Principal Component Analysis, 主成分分析）

• 原理：

  • 目标是找到一组新的正交坐标轴（主成分），使得投影后的数据方差最大。

  • 核心是对协方差矩阵做特征值分解（或 SVD），选择前 k 个最大特征值对应的特征向量作为新基。

  • 数学公式：

    max⁡w Var(wTX),s.t. ∥w∥=1\max_{w} \ Var(w^T X), \quad \text{s.t. } \|w\|=1wmax Var(wTX),s.t. ∥w∥=1

    即寻找最大化方差的方向 w。

• 应用场景：

  • 数据可视化（高维数据 → 2D/3D）

  • 特征压缩（减少维度但保留大部分信息）

  • 去噪（保留主成分，丢掉小方差噪声）

3️.LDA（Linear Discriminant Analysis, 线性判别分析）

• 原理：

  • 与 PCA 不同，LDA 是有监督的 降维方法。

    LDA和PCA有点像，但它是有监督的，会用到类别标签。它的目标是让同一类的数据尽量靠近，不同类的数据尽量分开，也就是增强类间差异、减小类内差异

  • 目标是寻找投影方向，使得 类间方差最大化，类内方差最小化，从而提升类别可分性。

  • 数学公式：

    J(w)=wTSbwwTSwwJ(w) = \frac{w^T S_b w}{w^T S_w w}J(w)=wTSwwwTSbw

    其中 S_b 为类间散度矩阵，SwS_wSw为类内散度矩阵，优化目标是最大化 Fisher 判别准则。

• 应用场景：

  • 分类任务中的降维（例如人脸识别，把高维像素数据投影到低维空间便于分类）。

  • 当类别标签已知时，比 PCA 更适合。

4. PCA vs LDA 对比

方法	是否监督	优化目标	应用场景
PCA	无监督	最大化投影方差	压缩数据、可视化、降噪
LDA	有监督	最大化类间距 / 最小化类内距	分类任务中的降维、人脸识别

一句话总结：

• PCA 关注"数据整体的方差最大化"，无监督，适合通用数据降维。

• LDA 关注"类别区分度最大化"，有监督，适合分类任务降维。

---

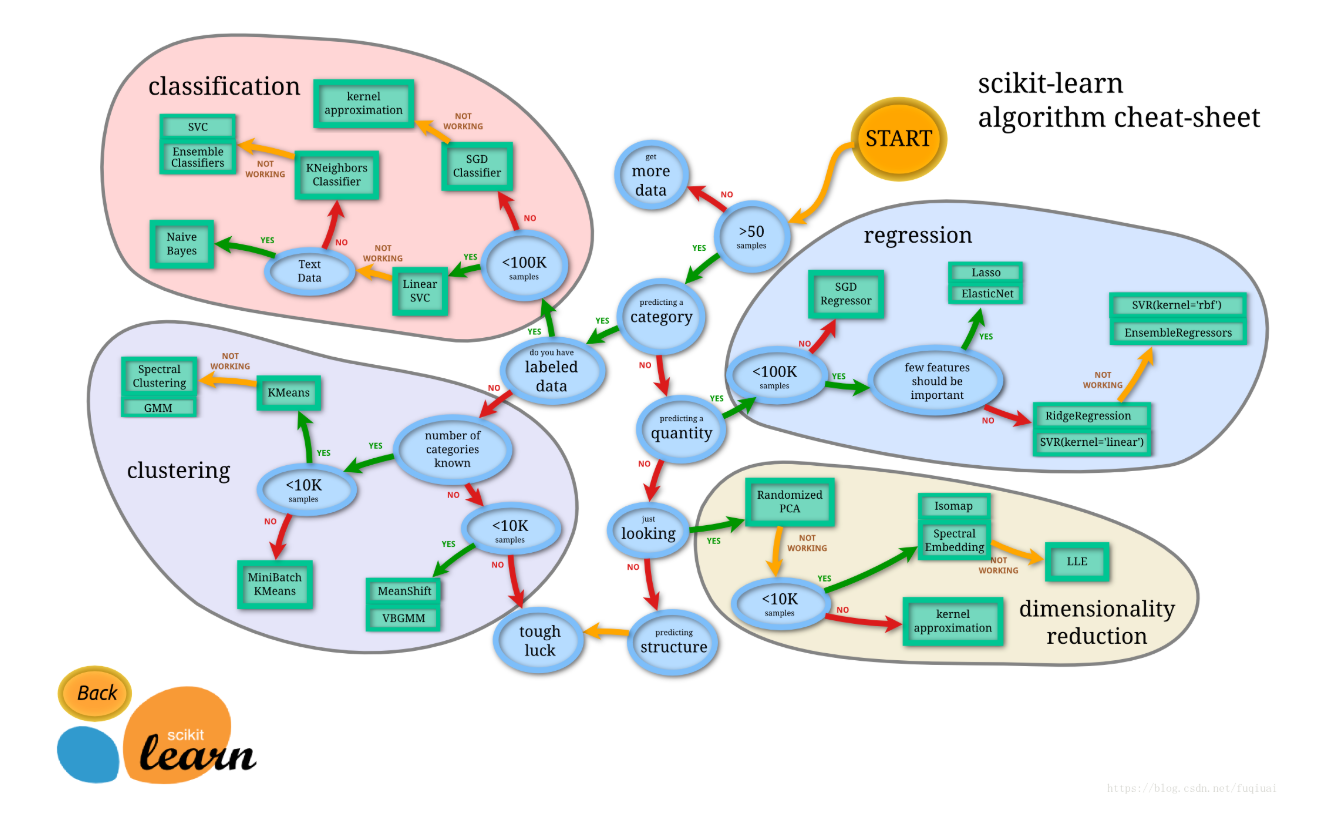
问题6：常见机器学习算法有哪些？比如线性回归、逻辑回归、决策树、随机森林、KNN、SVM、K-means、PCA，各自的原理、优缺点和适用场景如何？

1. 监督学习（有标签）

（1）线性回归（Linear Regression）

• 原理：假设输入和输出是线性关系，最小化平方误差。

• 优点：简单、可解释性强，计算高效。

• 缺点：无法拟合非线性，易受异常值影响。

• 应用：房价预测、销售预测。

（2）逻辑回归（Logistic Regression）

• 原理：通过 Sigmoid 函数将线性组合映射到 [0,1]，用于二分类。

• 优点：实现简单、概率输出、可解释性强。

• 缺点：只能处理线性可分问题，效果受特征工程影响大。

• 应用：垃圾邮件识别、信用风险预测。

（3）决策树（Decision Tree）

• 原理：基于特征划分数据，最小化熵或基尼指数，形成树结构。

• 优点：易理解，可处理非线性和类别型特征。

• 缺点：容易过拟合，对数据微小变化敏感。

• 应用：客户细分、医学诊断。

（4）随机森林（Random Forest）

• 原理：集成学习方法，训练多棵树（Bagging），投票/平均预测。

• 优点：鲁棒性好，泛化能力强，能评估特征重要性。

• 缺点：模型大，推理较慢，可解释性下降。

• 应用：信用评分、图像分类、推荐系统。

（5）KNN（K-Nearest Neighbors）

• 原理：根据最近的 k 个邻居投票或取均值进行分类/回归。

• 优点：实现简单，无需训练。

• 缺点：预测慢，对高维数据不适用，对噪声敏感。

• 应用：推荐系统、文本分类（小规模数据）。

（6）支持向量机（SVM）

• 原理：寻找最大化分类间隔的超平面，支持核方法处理非线性。

• 优点：适合小样本高维数据，理论基础扎实。

• 缺点：对大数据集训练慢，参数选择敏感。

• 应用：文本分类、人脸识别、生物信息学。

---

2. 无监督学习（无标签）

（7）K-means 聚类

• 原理：通过迭代更新簇中心和簇分配，最小化类内平方误差。

• 优点：实现简单、计算快。

• 缺点：需预设簇数，对初始点和异常值敏感，只能发现凸形簇。

• 应用：用户分群、图像分割、市场细分。

---

3. 降维方法

（8）PCA（主成分分析）

• 原理：寻找最大化方差的正交方向，将高维数据投影到低维空间。

• 优点：降维速度快，保留主要信息，去噪。

• 缺点：仅适合线性关系，不考虑标签信息。

• 应用：特征压缩、数据可视化、预处理。

---

问题7：集成学习方法有哪些？请分别说明 Bagging 和 Boosting（如 AdaBoost、Gradient Boosting、XGBoost）的原理及区别

1️.集成学习方法分类

常见的三类方法：

1. Bagging（Bootstrap Aggregating） → 并行训练，降低方差。

2. Boosting → 顺序训练，降低偏差。

3. Stacking → 多层模型融合，用元学习器综合不同模型。

2️. Bagging

• 原理：

  • 从原始数据集中有放回地随机采样，生成多个子数据集；

  • 在这些数据集上分别训练多个基学习器（通常是决策树）；

  • 最终结果通过投票（分类）或平均（回归）得到。

• 代表算法：随机森林（Random Forest）。

• 优点：

  • 降低方差，提升稳定性；

  • 对噪声数据鲁棒。

• 缺点：

  • 对弱学习器的偏差无能为力（即模型本身太弱也不行）。

• 适用场景：当单模型容易过拟合时（如决策树），用 Bagging 可以稳健化。

---

3️.Boosting

• 原理：

  • 顺序地训练多个弱学习器，每一步都关注前一轮做错的样本。

  • 通过不断调整样本权重或残差，逐渐提升整体模型的拟合能力。

• 代表算法：

  • AdaBoost

    • 核心思想：错分样本权重 ↑，正确样本权重 ↓；每个基学习器投票时权重 ∝ 准确率。

    • 优点：对弱分类器（如决策树桩）提升显著。

    • 缺点：对噪声和异常值敏感。

  • Gradient Boosting（GBDT）

    • 核心思想：通过梯度下降的方式拟合残差（每一轮新树学习前一轮的残差）。

    • 优点：拟合能力强，能处理复杂数据。

    • 缺点：训练慢，难以并行化。

  • XGBoost

    • 对 GBDT 的优化版本：二阶导数近似 + 正则化 + 并行化 + 缺失值处理。

    • 优点：计算效率高，泛化能力强。

    • 应用：竞赛常用模型，Kaggle、天池夺冠神器。

一句话总结：

• Bagging：并行训练 → 稳定、抗过拟合（典型：随机森林）。

• Boosting：顺序训练 → 不断修正偏差，拟合能力强（典型：AdaBoost、GBDT、XGBoost）。

问题8：说说神经网络的基本结构、前向传播与反向传播原理，以及激活函数（如 ReLU、Sigmoid、Tanh）的选择影响。

1️.神经网络的基本结构

• 神经元（Neuron）：仿生于生物神经元，接收输入 xx，经过加权求和再加偏置，输出结果。

  z=wTx+bz = w^T x + bz=wTx+b

• 层（Layer）：

  • 输入层：接收特征。

  • 隐藏层：多层神经元组合，负责特征提取。

  • 输出层：给出预测结果。

• 网络（Network）：多层感知机（MLP）、卷积神经网络（CNN）、循环神经网络（RNN）等。

---

2️.前向传播（Forward Propagation）

• 过程：数据从输入层流向输出层，逐层线性变换 + 非线性激活。

  a(l)=f(W(l)a(l−1)+b(l))a^{(l)} = f(W^{(l)} a^{(l-1)} + b^{(l)})a(l)=f(W(l)a(l−1)+b(l))

  • 其中 a(l)a^{(l)}a(l) 是第 ll 层的输出，f(⋅)f(\cdot)f(⋅) 是激活函数。

• 目标 ：得到预测值 y^\hat{y}y^。

• 损失函数：度量预测值与真实值的差异（如 MSE、交叉熵）。

---

3️.反向传播（Backpropagation, BP）

• 核心思想：基于链式法则计算损失函数对每层参数的梯度。

• 步骤：

  1. 前向传播：计算输出和损失。

  2. 反向传播：

     • 从输出层开始，计算损失对输出的导数。

     • 逐层利用链式法则传递梯度：

       ∂L∂W(l)=δ(l)(a(l−1))T\frac{\partial L}{\partial W^{(l)}} = \delta^{(l)} (a^{(l-1)})^T∂W(l)∂L=δ(l)(a(l−1))T

     • 其中 δ(l)\delta^{(l)}δ(l)是误差项。

  3. 更新参数：梯度下降或变种（SGD, Adam）。

• 作用：保证神经网络能逐步减少损失，学到合适的参数。

---

4️.激活函数（Activation Function）

（1）Sigmoid

f(x)=11+e−xf(x) = \frac{1}{1+e^{-x}}f(x)=1+e−x1

• 优点：输出在 (0,1)，可解释为概率。

• 缺点：容易梯度消失，收敛慢。

• 应用：二分类输出层。

（2）Tanh

f(x)=ex−e−xex+e−xf(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}}f(x)=ex+e−xex−e−x

• 优点：输出在 (-1,1)，比 Sigmoid 收敛快。

• 缺点：仍可能梯度消失。

• 应用：早期 RNN。

（3）ReLU（Rectified Linear Unit）

f(x)=max⁡(0,x)f(x) = \max(0, x)f(x)=max(0,x)

• 优点：计算简单，收敛快，缓解梯度消失。

• 缺点：可能出现"神经元死亡"（输出恒为 0）。

• 应用：深度网络主流激活函数。

（4）改进型 ReLU

• Leaky ReLU：允许负半轴有小斜率，缓解死亡问题。

• ELU / GELU / Swish：在深度网络中表现更好，常见于 Transformer、BERT。

一句话记忆：前向传播算预测，反向传播算梯度，激活函数给非线性 → 这样神经网络才"能学会"。

问题9：模型评估有哪些指标？如混淆矩阵、ROC 曲线、AUC、F1-score 等指标及其应用场景。

1️.基础指标（基于混淆矩阵）

假设二分类，混淆矩阵定义如下：

||预测正类 §|预测负类 (N)|

|实际正类 §|TP（真正例）|FN（假负例）|

|实际负类 (N)|FP（假正例）|TN（真负例）|

• 准确率（Accuracy）：

  TP+TNTP+TN+FP+FN\frac{TP + TN}{TP+TN+FP+FN}

  → 衡量整体预测正确比例。

  → 适合样本均衡的数据集。

• 精确率（Precision）：

  TPTP+FP\frac{TP}{TP+FP}

  → 在预测为正的样本中，真正为正的比例。

  → 关注 预测结果的准确性（少错杀）。

• 召回率（Recall, Sensitivity）：

  TPTP+FN\frac{TP}{TP+FN}

  → 在所有实际为正的样本中，正确识别出的比例。

  → 关注 覆盖率（少漏报）。

---

2️. 综合指标

• F1-score：精确率和召回率的调和平均。

  F1=2⋅Precision⋅RecallPrecision+RecallF1 = \frac{2 \cdot Precision \cdot Recall}{Precision + Recall}

  → 适合类别不平衡时综合考量。

• 宏平均（Macro Average）：对每一类分别计算指标，再取平均（各类同等重要）。

• 微平均（Micro Average）：先汇总所有 TP/FP/FN/TN，再计算指标（考虑样本量差异）。

---

3️.ROC 曲线与 AUC

• ROC 曲线（Receiver Operating Characteristic Curve）：

  • 横轴：FPR（假正例率） = FP / (FP+TN)

  • 纵轴：TPR（真正例率，即 Recall） = TP / (TP+FN)

  • 描述分类器在不同阈值下的性能。

• AUC（Area Under Curve）：ROC 曲线下的面积，取值范围 [0,1]。

  • AUC 越接近 1，模型区分正负样本能力越强。

  • AUC=0.5 → 随机猜测。

---

4️.适用场景

• 准确率：样本均衡时常用（如手写数字识别）。

• Precision & Recall：类别不平衡时需结合使用。

  • 高 Precision：适合垃圾邮件过滤（宁可少拦，也不能错拦重要邮件）。

  • 高 Recall：适合医学诊断（宁可多报，也不能漏掉患者）。

• F1-score：在 Precision 和 Recall 之间平衡时使用（如信息检索）。

• ROC/AUC：评估模型区分能力，特别在阈值不确定时（如信用评分、风控模型）。

---

一句话总结：

• Accuracy：整体正确率。

• Precision：预测结果的可靠性。

• Recall：正样本的覆盖率。

• F1：精确率和召回率的平衡。

• ROC/AUC：模型区分能力的全局评价。

问题10：常见的模型调参方法有哪些？如网格搜索、随机搜索、贝叶斯优化等，你如何选择？

1️.网格搜索（Grid Search）

• 原理：

  • 预先设定一个参数网格（如学习率 ∈ {0.01,0.1}, 树深度 ∈ {3,5,7}），枚举所有组合，逐一训练模型。

• 优点：

  • 实现简单，结果可重复。

• 缺点：

  • 计算开销大，维度灾难（参数多时爆炸）。

• 适用场景：

  • 参数少，取值范围有限（如 SVM 的 C、γ）。

---

2️.随机搜索（Random Search）

• 原理：

  • 从参数空间中随机采样若干组参数进行训练，而不是全覆盖。

• 优点：

  • 在相同计算预算下，比网格搜索更可能找到接近最优解；适合高维空间。

• 缺点：

  • 不能保证覆盖关键参数点，结果有随机性。

• 适用场景：

  • 参数空间较大，不清楚哪些参数重要。

---

3️.贝叶斯优化（Bayesian Optimization）

• 原理：

  • 通过构建代理模型（如高斯过程 GP）来近似"超参数 → 性能"的函数；

  • 根据代理模型和采集函数（如 UCB, EI）选择下一组参数，平衡"探索 vs 利用"。

• 优点：

  • 利用历史调参结果，效率高；适合计算代价昂贵的模型。

• 缺点：

  • 实现复杂，代理模型本身需要计算。

• 适用场景：

  • 深度学习、XGBoost 等训练耗时较长的模型。

---

4️.其他方法

• 超参数进化（Genetic Algorithm / Population Based Training, PBT）：用进化策略迭代更新参数，适合大规模分布式环境。

• Hyperband / Successive Halving：动态分配计算资源，快速淘汰表现差的参数组合。

• Optuna / Ray Tune 等自动调参工具：结合多种方法，支持分布式并行搜索。

---

5️. 如何选择？

• 小参数空间（少量关键参数） → 网格搜索。

• 大参数空间，但训练代价低 → 随机搜索。

• 大参数空间，训练代价高 → 贝叶斯优化 / Hyperband。

• 深度学习分布式训练 → PBT / Optuna。

一句话总结：

• 网格搜索 = "笨办法"，适合小空间。

• 随机搜索 = "性价比高的盲盒"。

• 贝叶斯优化 = "聪明探索"，适合大模型。