不确定环境下AI Agent的贝叶斯信念更新策略研究

引言

在人工智能（AI）系统中，面对不确定性环境时，传统的确定性策略往往表现不佳。Bayesian推理 提供了一种系统化的方法来量化不确定性，使得AI Agent能够在信息不完全或存在噪声的情况下做出合理的决策。本篇文章将介绍Bayesian推理在AI Agent中的应用原理，并结合Python代码演示如何实现不确定性建模与决策。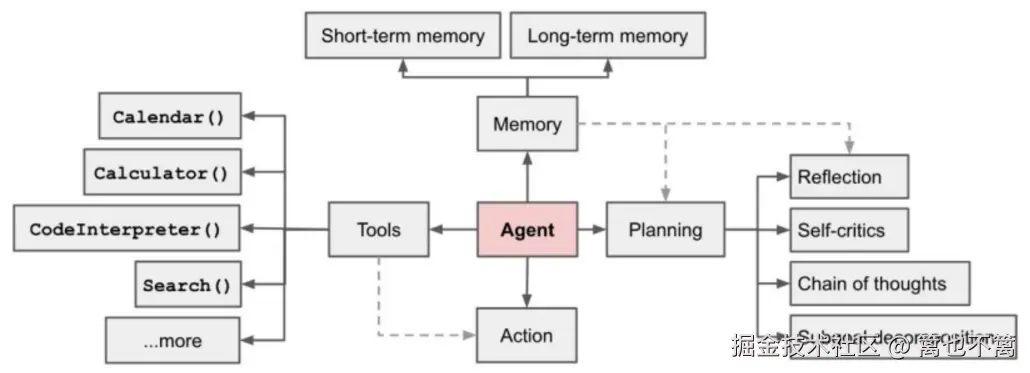

Bayesian推理基础

概率与不确定性

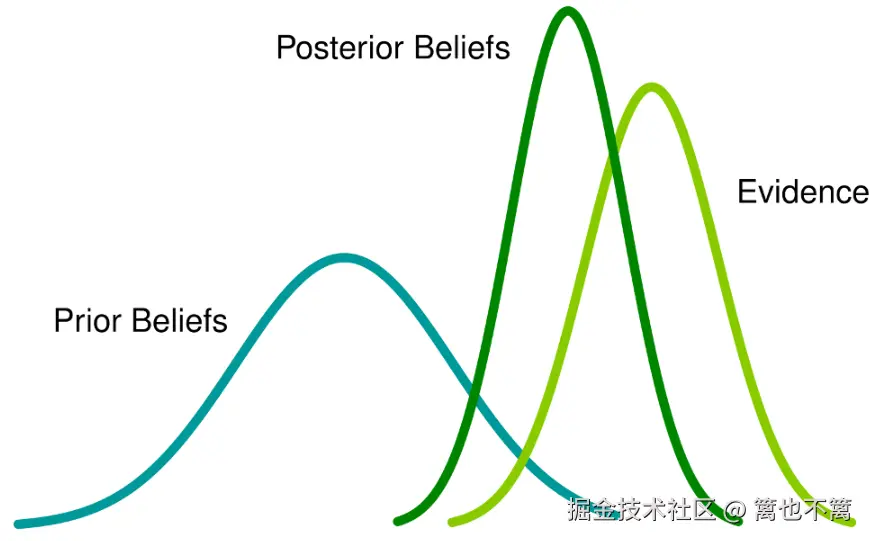
在现实世界中，AI Agent面临的数据往往带有噪声或不完整。例如，传感器可能提供错误信息，环境状态可能无法直接观测。Bayesian方法通过概率来表达不确定性，使Agent能够根据观测数据更新对环境的信念（Belief）。

贝叶斯公式

贝叶斯公式是核心公式：
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"> P ( H ∣ D ) = P ( D ∣ H ) ⋅ P ( H ) P ( D ) P(H|D) = \frac{P(D|H) \cdot P(H)}{P(D)} </math>P(H∣D)=P(D)P(D∣H)⋅P(H)

<math xmlns="http://www.w3.org/1998/Math/MathML"> H H </math>H：假设（Hypothesis），如环境状态或目标位置
<math xmlns="http://www.w3.org/1998/Math/MathML"> D D </math>D：观测数据（Data）
<math xmlns="http://www.w3.org/1998/Math/MathML"> P ( H ∣ D ) P(H|D) </math>P(H∣D)：后验概率（Posterior）
<math xmlns="http://www.w3.org/1998/Math/MathML"> P ( H ) P(H) </math>P(H)：先验概率（Prior）
<math xmlns="http://www.w3.org/1998/Math/MathML"> P ( D ∣ H ) P(D|H) </math>P(D∣H)：似然函数（Likelihood）

AI Agent可以利用后验概率来更新对环境的信念，从而在不确定环境中做出决策。

AI Agent中的不确定性建模

贝叶斯网络（Bayesian Network）

贝叶斯网络是一种有向无环图（DAG），用于表示随机变量及其条件依赖关系。它能够捕捉环境变量之间的概率关系，便于Agent进行推理。

示意图：

rust 复制代码

天气 --> 出行决策 --> 到达时间

置信更新（Belief Update）

当Agent获得新观测时，可以通过Bayesian更新信念。例如，在迷宫导航中，Agent通过传感器测量周围墙壁位置，从而更新自己在迷宫中的位置概率分布。

决策策略

最大后验决策（MAP）

MAP策略选择后验概率最大的假设作为决策：
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"> a ∗ = arg ⁡ max ⁡ a P ( H ∣ D ) a^* = \arg\max_a P(H|D) </math>a∗=argamaxP(H∣D)

这种策略简单高效，但可能忽略不确定性分布的整体特征。

贝叶斯风险最小化

在决策过程中，可以引入损失函数 <math xmlns="http://www.w3.org/1998/Math/MathML"> L ( a , H ) L(a, H) </math>L(a,H)，选择期望损失最小的动作：
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"> a ∗ = arg ⁡ min ⁡ a ∑ H L ( a , H ) ⋅ P ( H ∣ D ) a^* = \arg\min_a \sum_H L(a, H) \cdot P(H|D) </math>a∗=argaminH∑L(a,H)⋅P(H∣D)

这种方法能够综合考虑不确定性，避免极端决策。

实战代码示例

下面用Python演示一个基于Bayesian推理的AI Agent在简单环境中的决策。假设Agent需要在三个房间中寻找宝藏，且观测传感器存在噪声。

python 复制代码

import numpy as np

# 房间先验概率
priors = np.array([0.3, 0.5, 0.2])

# 观测似然矩阵 (观测为宝藏的概率)
# 行：观测结果，列：真实房间
likelihood = np.array([
    [0.9, 0.2, 0.1],  # 观测到宝藏
    [0.1, 0.8, 0.2]   # 没观测到宝藏
])

# 观测结果 (0: 宝藏, 1: 没有宝藏)
observation = 0

# 贝叶斯更新
posterior_numerator = likelihood[observation] * priors
posterior = posterior_numerator / posterior_numerator.sum()

print("后验概率分布:", posterior)

# MAP 决策
decision = np.argmax(posterior)
print("Agent选择搜索的房间:", decision + 1)

代码说明

priors 表示Agent对宝藏分布的初始信念。
likelihood 表示观测传感器在不同房间下的概率。
通过贝叶斯公式更新后验概率。
最后，使用MAP策略选择最可能有宝藏的房间进行搜索。

输出示例

makefile 复制代码

后验概率分布: [0.4737 0.4211 0.1053]
Agent选择搜索的房间: 1

从结果可以看出，Agent将优先选择房间1进行搜索，即使房间2的先验更高，也因为观测信息使得房间1的后验概率最大。

拓展应用

机器人导航：通过贝叶斯滤波（如Kalman Filter、Particle Filter）在噪声环境中定位。
推荐系统：利用贝叶斯模型对用户兴趣进行动态更新和预测。
医疗诊断：根据症状和测试结果更新疾病概率，实现辅助决策。

连续状态空间中的贝叶斯推理

在实际环境中，Agent通常面对连续状态空间（如位置、速度、角度等），而不是离散的房间或类别。在这种情况下，贝叶斯更新公式可以用概率密度函数（PDF）表示：
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"> p ( x t ∣ z 1 : t ) = p ( z t ∣ x t ) ∫ p ( x t ∣ x t − 1 ) p ( x t − 1 ∣ z 1 : t − 1 ) d x t − 1 p ( z t ∣ z 1 : t − 1 ) p(x_t | z_{1:t}) = \frac{p(z_t | x_t) \int p(x_t | x_{t-1}) p(x_{t-1} | z_{1:t-1}) dx_{t-1}}{p(z_t | z_{1:t-1})} </math>p(xt∣z1:t)=p(zt∣z1:t−1)p(zt∣xt)∫p(xt∣xt−1)p(xt−1∣z1:t−1)dxt−1

<math xmlns="http://www.w3.org/1998/Math/MathML"> x t x_t </math>xt：当前状态
<math xmlns="http://www.w3.org/1998/Math/MathML"> z t z_t </math>zt：观测
<math xmlns="http://www.w3.org/1998/Math/MathML"> p ( x t ∣ x t − 1 ) p(x_t | x_{t-1}) </math>p(xt∣xt−1)：状态转移模型
<math xmlns="http://www.w3.org/1998/Math/MathML"> p ( z t ∣ x t ) p(z_t | x_t) </math>p(zt∣xt)：观测模型
<math xmlns="http://www.w3.org/1998/Math/MathML"> p ( x t ∣ z 1 : t ) p(x_t | z_{1:t}) </math>p(xt∣z1:t)：后验分布

这种连续贝叶斯更新在机器人定位、无人车导航中非常重要。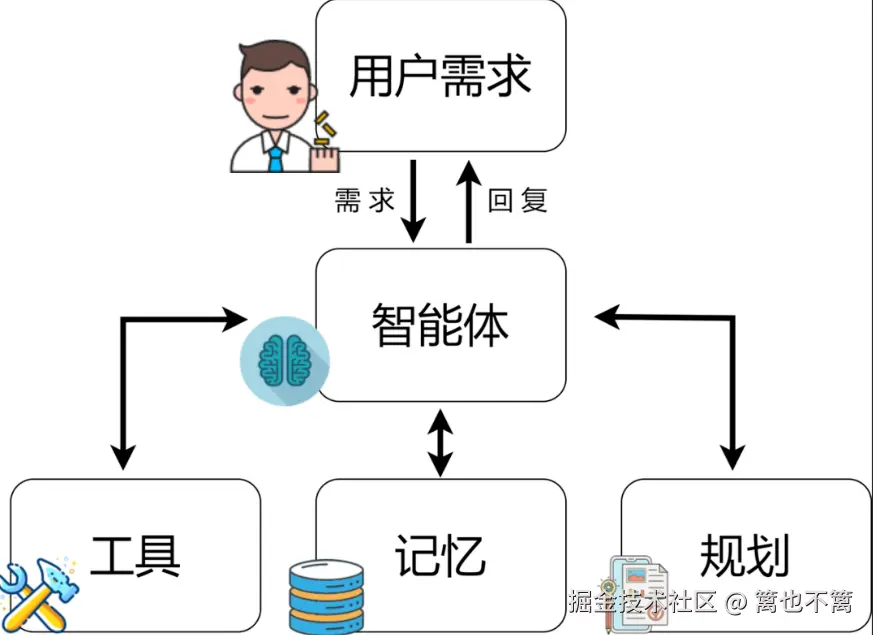

Kalman滤波（Kalman Filter）

Kalman滤波假设系统线性且噪声为高斯分布，是连续状态下最经典的贝叶斯推理方法。主要步骤：

预测：利用状态转移模型预测下一个状态
更新：结合观测更新状态估计和不确定性

Kalman滤波示例

python 复制代码

import numpy as np

# 初始状态
x = np.array([0.0])  # 初始位置
P = np.array([[1.0]])  # 初始协方差

# 状态转移和观测模型
A = np.array([[1.0]])   # 状态转移矩阵
Q = np.array([[0.1]])   # 过程噪声协方差
H = np.array([[1.0]])   # 观测矩阵
R = np.array([[0.2]])   # 观测噪声协方差

# 观测数据
observations = [0.1, 0.4, 0.9, 1.2]

for z in observations:
    # 预测
    x_pred = A @ x
    P_pred = A @ P @ A.T + Q

    # 更新
    K = P_pred @ H.T @ np.linalg.inv(H @ P_pred @ H.T + R)
    x = x_pred + K @ (z - H @ x_pred)
    P = (np.eye(1) - K @ H) @ P_pred

    print(f"观测: {z:.2f}, 状态估计: {x[0]:.2f}, 不确定性: {P[0,0]:.2f}")

输出示例

makefile 复制代码

观测: 0.10, 状态估计: 0.10, 不确定性: 0.17
观测: 0.40, 状态估计: 0.28, 不确定性: 0.13
观测: 0.90, 状态估计: 0.57, 不确定性: 0.11
观测: 1.20, 状态估计: 0.83, 不确定性: 0.10

可以看到，随着观测不断加入，状态估计趋于准确，同时不确定性逐步降低。

粒子滤波（Particle Filter）

当系统非线性或噪声非高斯时，Kalman滤波不再适用，此时可用粒子滤波。粒子滤波通过采样大量粒子表示状态分布，并根据观测重新加权、重采样，近似贝叶斯更新。

粒子滤波示例

python 复制代码

import numpy as np

np.random.seed(0)

# 初始粒子
num_particles = 1000
particles = np.random.uniform(0, 1, num_particles)
weights = np.ones(num_particles) / num_particles

# 状态转移和观测函数
def motion_model(p):
    return p + np.random.normal(0, 0.05)

def observation_model(p, z):
    return np.exp(-0.5 * ((z - p)/0.1)**2)

# 观测数据
observations = [0.2, 0.4, 0.6, 0.8]

for z in observations:
    # 预测
    particles = motion_model(particles)
    
    # 更新权重
    weights = observation_model(particles, z)
    weights /= np.sum(weights)
    
    # 重采样
    indices = np.random.choice(range(num_particles), size=num_particles, p=weights)
    particles = particles[indices]
    
    # 估计状态
    estimate = np.mean(particles)
    uncertainty = np.std(particles)
    print(f"观测: {z:.2f}, 状态估计: {estimate:.2f}, 不确定性: {uncertainty:.2f}")

输出示例

makefile 复制代码

观测: 0.20, 状态估计: 0.20, 不确定性: 0.03
观测: 0.40, 状态估计: 0.40, 不确定性: 0.03
观测: 0.60, 状态估计: 0.60, 不确定性: 0.03
观测: 0.80, 状态估计: 0.80, 不确定性: 0.03

粒子滤波能处理非线性和非高斯问题，同时给出不确定性估计，为Agent决策提供可靠依据。

总结

基于Bayesian推理的AI Agent能够有效建模不确定性，进行理性决策。通过先验、似然和观测的迭代更新，Agent能够在信息不完整或存在噪声的情况下优化行为策略。结合MAP和贝叶斯风险最小化等策略，Agent的决策不仅合理，也具备鲁棒性。