本文主要介绍图像增强,包括灰度变换增强(线性增强、对数增强、指数增强)、空间滤波增强、频域增强和主成分增强。同时附上了各种方法的原理解释和代码示例。
1. 图像增强的作用
图像增强(Image Enhancement)的目标是 突出目标特征、抑制无关信息 ,使图像更适合人眼观察或后续的计算机处理。
增强操作不会创造新的信息,但能提高已有信息的可见性。
2. 图像增强的主要类别
(1) 灰度变换增强
原理 :对图像像素灰度值 r r r 进行函数变换 ,得到新的输出灰度 s s s:
s = T ( r ) s = T(r) s=T(r)
常见形式:
- 线性变换 : s = a r + b s = a r + b s=ar+b (对比度拉伸、亮度调整)
- 对数变换 : s = c log ( 1 + r ) s = c \log(1 + r) s=clog(1+r) (增强暗部细节)
- 指数变换 : s = c r γ s = c r^\gamma s=crγ (伽马校正, γ < 1 \gamma < 1 γ<1 增强暗部, γ > 1 \gamma > 1 γ>1 增强亮部)
代码示例(灰度变换)
示例图片下载链接:lena 然后把图片放到工作目录下即可
python
import cv2
import numpy as np
import matplotlib.pyplot as plt
# 读取示例图像(grayscale)
img = cv2.imread("lena.jpg", cv2.IMREAD_GRAYSCALE)
# 线性变换:增强对比度
linear = cv2.convertScaleAbs(img, alpha=1.5, beta=30)
# 对数变换
log = (np.log1p(img.astype(np.float32)) / np.log(256)) * 255
log = np.uint8(log)
# 伽马变换
gamma = np.power(img/255.0, 0.5) * 255
gamma = np.uint8(gamma)
# 显示结果
titles = ["Original", "Linear", "Log", "Gamma (0.5)"]
images = [img, linear, log, gamma]
plt.figure(figsize=(10,6))
for i in range(4):
plt.subplot(2,2,i+1)
plt.imshow(images[i], cmap="gray")
plt.title(titles[i])
plt.axis("off")
plt.show()结果:

这几种图像变换效果如下:
Linear(线性变换) :整体亮度和对比度都被增强。图像看起来更加明亮,暗部和亮部的细节都更加突出。常用来做简单的增强处理。
Log(对数变换) :对数变换能提升图像中暗部细节 ,使低灰度值区域变得更亮,而高灰度值区域的变化较小。
Gamma (0.5)(伽马变换):伽马值小于1时(如0.5),整体图像变得更亮,尤其是暗部区域更加突出。
(2) 空间滤波增强
原理
通过邻域运算利用卷积核处理图像:
g ( x , y ) = ∑ i = − m m ∑ j = − n n f ( x + i , y + j ) ⋅ h ( i , j ) g(x,y) = \sum_{i=-m}^{m} \sum_{j=-n}^{n} f(x+i, y+j) \cdot h(i,j) g(x,y)=i=−m∑mj=−n∑nf(x+i,y+j)⋅h(i,j)
其中 h ( i , j ) h(i,j) h(i,j) 是滤波器(卷积核)。
- 平滑滤波:抑制噪声(均值滤波、高斯滤波)。
- 锐化滤波:增强边缘(Sobel、Laplacian、高通滤波)。
代码示例(平滑 vs 锐化)
python
# 均值滤波(平滑)
blur = cv2.blur(img, (5,5))
# 高斯滤波(平滑)
gaussian = cv2.GaussianBlur(img, (5,5), 1)
# Laplacian(锐化)
laplacian = cv2.Laplacian(img, cv2.CV_64F)
laplacian = cv2.convertScaleAbs(laplacian)
# Sobel(锐化,检测边缘)
sobel = cv2.Sobel(img, cv2.CV_64F, 1, 1, ksize=5)
sobel = cv2.convertScaleAbs(sobel)
# 显示结果
titles = ["Original", "Blur", "Gaussian", "Laplacian", "Sobel"]
images = [img, blur, gaussian, laplacian, sobel]
plt.figure(figsize=(12,6))
for i in range(5):
plt.subplot(2,3,i+1)
plt.imshow(images[i], cmap="gray")
plt.title(titles[i])
plt.axis("off")
plt.show()结果:

这几种变换的效果如下:
Blur(均值模糊)
通过均值滤波,对图像进行简单模糊处理,图像整体变得柔和,细节变少,边缘变得不明显。
Gaussian(高斯)
用高斯核对图像进行模糊处理,相比均值模糊,能更自然地模糊图像,去除噪声,同时保留更多的整体结构。
Laplacian(拉普拉斯变换)
这是一种边缘检测算子,突出图像中的边缘和细节。变换后,只有图像中的轮廓和边缘被高亮显示,其他区域变暗。
Sobel(Sobel算子)
另一种常见的边缘检测方法,可以突出图像中的水平和垂直边缘。处理后,图像中的轮廓和结构更加明显,便于分析纹理和物体边界。
(3) 频域增强
原理
利用傅里叶变换:
F ( u , v ) = ∑ x = 0 M − 1 ∑ y = 0 N − 1 f ( x , y ) e − j 2 π ( u x M + v y N ) F(u,v) = \sum_{x=0}^{M-1}\sum_{y=0}^{N-1} f(x,y)e^{-j2\pi\left(\frac{ux}{M} + \frac{vy}{N}\right)} F(u,v)=x=0∑M−1y=0∑N−1f(x,y)e−j2π(Mux+Nvy)
通过 滤波器函数 H ( u , v ) H(u,v) H(u,v) 调整频率分量:
G ( u , v ) = H ( u , v ) ⋅ F ( u , v ) G(u,v) = H(u,v)\cdot F(u,v) G(u,v)=H(u,v)⋅F(u,v)
- 低通滤波:保留低频,去除高频噪声。
- 高通滤波:保留高频,增强边缘。
代码示例(频域低通/高通)
python
# 傅里叶变换
f = np.fft.fft2(img)
fshift = np.fft.fftshift(f)
rows, cols = img.shape
crow, ccol = rows//2, cols//2
# 低通滤波器 (圆形掩膜)
mask_low = np.zeros((rows, cols), np.uint8)
r = 30
cv2.circle(mask_low, (ccol, crow), r, 1, -1)
# 高通滤波器 = 1 - 低通
mask_high = 1 - mask_low
# 应用滤波
low = fshift * mask_low
high = fshift * mask_high
# 逆变换
low_img = np.fft.ifft2(np.fft.ifftshift(low))
low_img = np.abs(low_img)
high_img = np.fft.ifft2(np.fft.ifftshift(high))
high_img = np.abs(high_img)
# 显示结果
plt.figure(figsize=(10,6))
plt.subplot(1,3,1), plt.imshow(img, cmap="gray"), plt.title("Original")
plt.subplot(1,3,2), plt.imshow(low_img, cmap="gray"), plt.title("Low-pass")
plt.subplot(1,3,3), plt.imshow(high_img, cmap="gray"), plt.title("High-pass")
plt.show()结果:
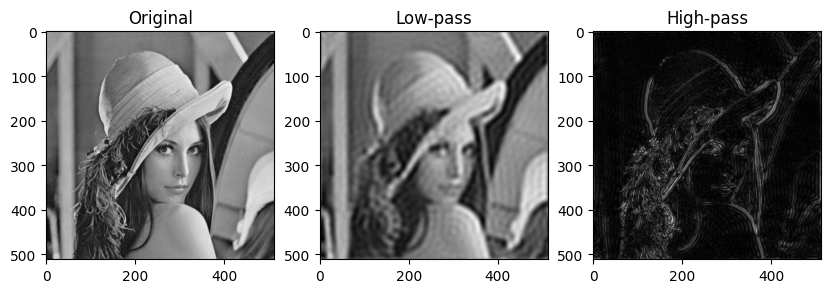
这三种变换效果如下:
Low-pass(低通高斯)
低通高斯滤波主要去除图像中的高频信息,保留了图像的整体结构和低频部分,因此图像变得更加平滑,细节被模糊。
High-pass(高通高斯)
高通高斯滤波突出图像中的高频信息,主要表现为边缘和细节增强,去除了平滑区域和低频部分。
(4) 主成分/彩色合成增强
原理
多波段图像(如遥感影像)中,波段间存在相关性。
利用 主成分分析(PCA),将多波段数据投影到少数几个新坐标轴(主成分),提升特征可见性:
Y = W T X , W = [ v 1 , v 2 , ... , v k ] Y = W^T X, \quad W = [v_1, v_2, \dots, v_k] Y=WTX,W=[v1,v2,...,vk]
其中 v i v_i vi 是协方差矩阵的特征向量。
代码示例(三通道图像 PCA)
python
from sklearn.decomposition import PCA
# 读取彩色图像
color_img = cv2.imread(cv2.samples.findFile("lena.jpg"))
color_img = cv2.cvtColor(color_img, cv2.COLOR_BGR2RGB)
# 转换为二维 (像素, 波段)
X = color_img.reshape((-1, 3))
# PCA -> 3个主成分
pca = PCA(n_components=3)
X_pca = pca.fit_transform(X)
# 还原为图像
pca_img = X_pca.reshape(color_img.shape)
pca_img = cv2.normalize(pca_img, None, 0, 255, cv2.NORM_MINMAX).astype(np.uint8)
# 显示
plt.subplot(1,2,1), plt.imshow(color_img), plt.title("Original RGB")
plt.subplot(1,2,2), plt.imshow(pca_img), plt.title("PCA Enhanced")
plt.show()结果:
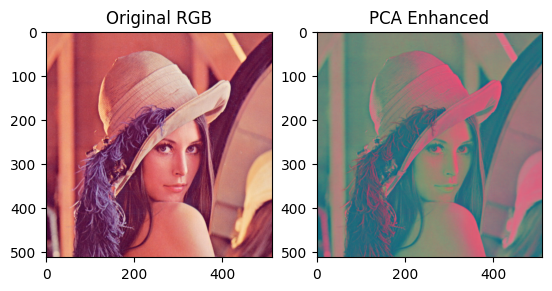
把原始RGB空间的颜色信息投影到新的主成分空间,使各个主成分最大程度地保留原始图像的主要信息和差异。PCA增强图像的颜色分布发生了明显变化,呈现出更强烈的色彩对比和分层感。
总结
图像增强分类:
- 灰度变换增强:改变灰度分布(线性、对数、伽马)。
- 空间滤波增强:利用卷积核进行平滑或锐化。
- 频域增强:在频谱域滤波,增强或抑制特定频率成分。
- 主成分/彩色合成增强:用于多波段图像,突出主要信息。