【动态规划】路径问题

• 一、[不同路径](https://leetcode.cn/problems/unique-paths/description/)
• [二、[不同路径 II](https://leetcode.cn/problems/unique-paths-ii/description/)](#二、不同路径 II)
• 三、[珠宝的最高价值](https://leetcode.cn/problems/li-wu-de-zui-da-jie-zhi-lcof/description/)
• 四、[下降路径最小和](https://leetcode.cn/problems/minimum-falling-path-sum/description/)
• 五、[最小路径和](https://leetcode.cn/problems/minimum-path-sum/description/)
• 六、[地下城游戏](https://leetcode.cn/problems/dungeon-game/description/)
• 结尾

一、不同路径

题目描述：

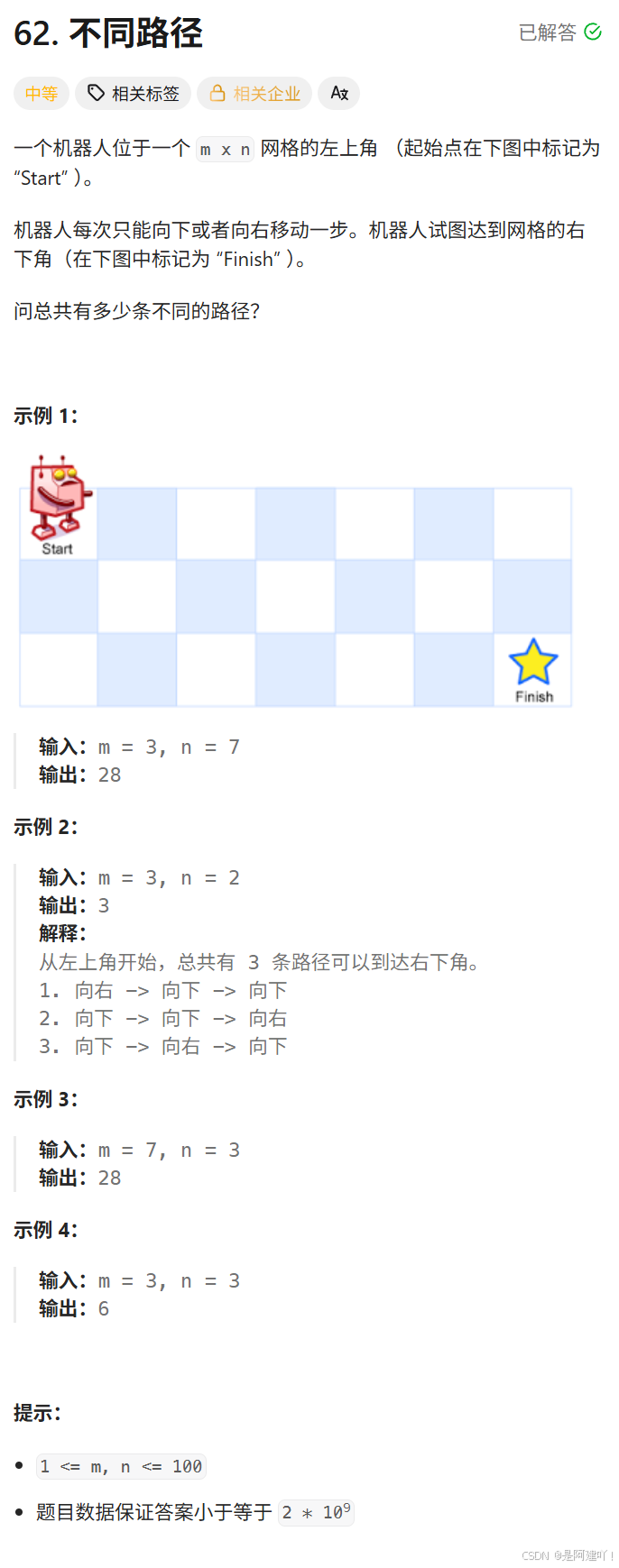
思路讲解：

本道题需要我们找出机器人从网格左上角（1,1）出发，只能向下或向右移动，目标是到达右下角（m,n），一个有多少条不同的路径，问题可拆解为：到达（i,j）的路径数 = 到达上方（i-1,j）的路径数 + 到达左侧（i,j-1）的路径数（因只能从这两个方向移动而来）。下面的思路中添加了虚拟行列，为了方便初始化，以下是具体思路：

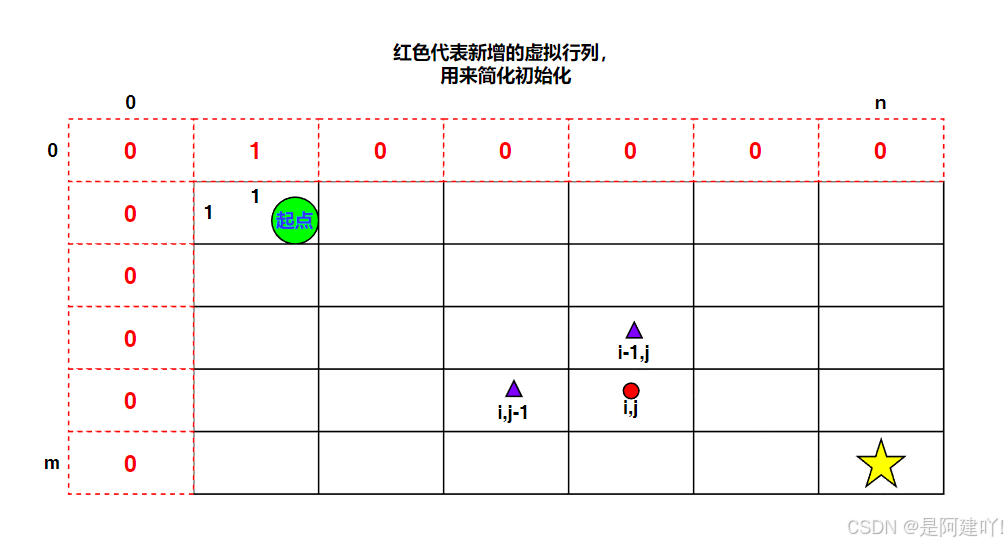
1. 状态表示：dp[i][j] 表示从左上角到达第 i 行第 j 列的不同路径总数
2. 状态转移方程 ：
   • 当前网格的路径数由上方和左侧网格的路径数累加得到：dp[i][j] = dp[i-1][j] + dp[i][j-1]
3. 初始化 ：
   • 通过巧妙设置初始状态简化边界处理，在上方添加一行，左方添加一列，并定义 dp[0][1] = 1，此设置确保：
     • 第一行（i=1）的所有网格 dp[1][j] 只能从左侧累加，因上方无网格（dp[0][j] = 0），故 dp[1][j] = dp[1][j-1]，符合 "只能一直向右移动" 的路径逻辑
     • 第一列（j=1）的所有网格 dp[i][1] 只能从上方累加，因左侧无网格（dp[i][0] = 0），故 dp[i][1] = dp[i-1][1]，符合 "只能一直向下移动" 的路径逻辑
4. 填写 DP 表 ：
   • 从上到下遍历每一行，每一行从左到右遍历网格：
     • 外层循环从 i=1 遍历到 i=m，内层循环从 j=1 遍历到 j=n
     • 每个 dp[i][j] 都基于已计算的上方（dp[i-1][j]）和左侧（dp[i][j-1]）结果，确保子问题已先求解
5. 结果返回 ：
   • 终点（m,n）的路径数存储在 dp[m][n] 中，直接返回即可

编写代码：

class Solution {
public:
    int uniquePaths(int m, int n) {
        vector<vector<int>> dp(m+1,vector<int>(n+1,0));

        dp[0][1] = 1;

        for(int i = 1 ; i <= m ; i++)
        {
            for(int j = 1 ; j <= n ; j++)
            {
                dp[i][j] = dp[i-1][j] + dp[i][j-1];
            }
        }

        return dp[m][n];
    }
};

---

二、不同路径 II

题目描述：

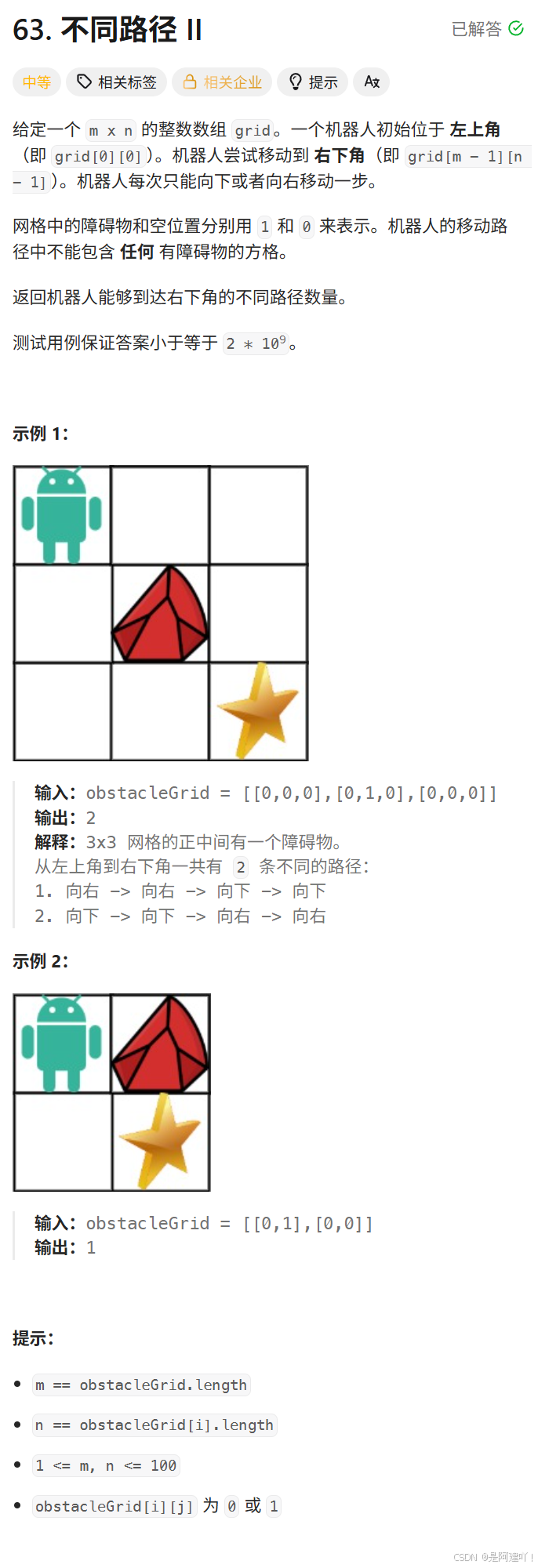
思路讲解：

本道题需要我们找出机器人从左上角（0,0）出发，只能向下或向右移动，目标是到达右下角（rows-1, cols-1），且路径中不能包含障碍物（值为 1 的格子），问题可拆解为：若当前格子无障碍物，到达（i,j）的路径数 = 到达上方（i-1,j）的路径数 + 到达左侧（i,j-1）的路径数；若有障碍物，则路径数为 0。下面的思路中添加了虚拟行列，为了方便初始化，以下是具体思路：

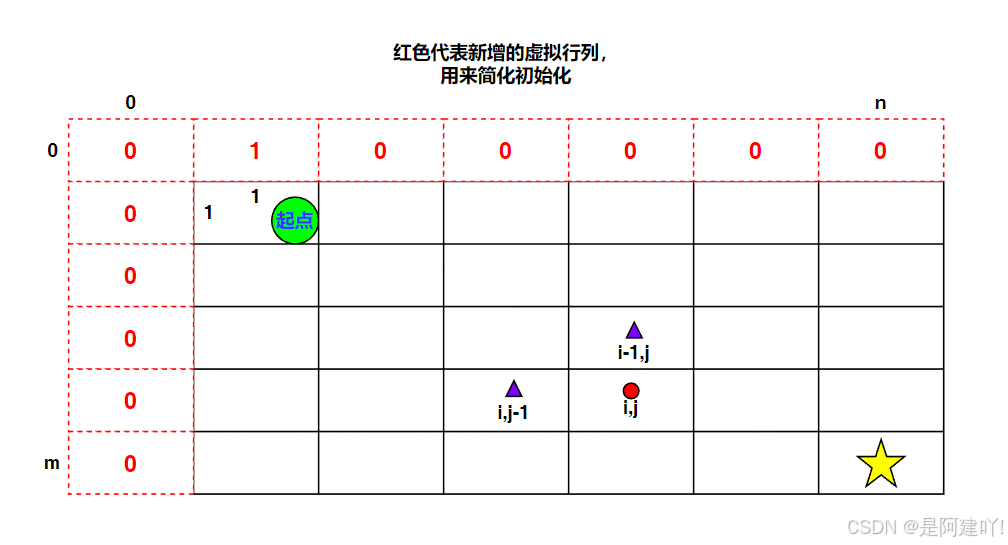
1. 状态表示：dp[i][j] 表示从左上角到达第 i 行第 j 列的不同有效路径总数（对应矩阵中 obstacleGrid[i-1][j-1]）
2. 状态转移方程 ：
   • 若当前网格 obstacleGrid[i-1][j-1] == 1（有障碍物），则 dp[i][j] = 0（直接跳过，保持初始值 0）
   • 若当前网格无障碍物，则 dp[i][j] = dp[i-1][j] + dp[i][j-1]，即上方路径数与左侧路径数之和
3. 初始化 ：
   • 通过巧妙设置初始状态简化边界处理，在上方添加一行，左方添加一列，并定义 dp[0][1] = 1，此设置确保：
     • 第一行（i=1）的网格若无障碍，只能从左侧累加路径数（因上方无网格）
     • 第一列（j=1）的网格若无障碍，只能从上方累加路径数（因左侧无网格）
     • 若起点（0,0）有障碍物，后续所有路径数自然为 0，符合逻辑
4. 填写 DP 表 ：
   • 从上到下遍历每一行，每一行从左到右遍历网格：
     • 外层循环从 i=1 到 rows，内层循环从 j=1 到 cols
     • 每个 dp[i][j] 仅依赖已计算的上方（dp[i-1][j]）和左侧（dp[i][j-1]）结果，确保子问题已求解
5. 结果返回 ：
   • 终点（rows-1, cols-1）的有效路径数存储在 dp[rows][cols] 中，直接返回即可

编写代码：

class Solution {
public:
    int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {
        int rows = obstacleGrid.size() , cols = obstacleGrid[0].size();
        vector<vector<int>> dp(rows + 1 , vector<int>(cols + 1,0));
        dp[0][1] = 1;

        for(int i = 1 ; i <= rows ; i++)
        {
            for(int j = 1 ; j <= cols ; j++)
            {
                if(obstacleGrid[i-1][j-1] == 1) continue;

                dp[i][j] = dp[i-1][j] + dp[i][j-1];
            }
        }

        return dp[rows][cols];
    }
};

---

三、珠宝的最高价值

题目描述：

思路讲解：

本道题需要我们从左上角出发，只能向右或向下移动，目标是到达右下角并获得最高总珠宝价值，问题可拆解为：到达（i,j）的最高价值 = 到达上方（i-1,j）或左侧（i,j-1）的最高价值（取较大者） + 当前位置的珠宝价值。下面的思路中添加了虚拟行列，为了方便初始化，以下是具体思路：

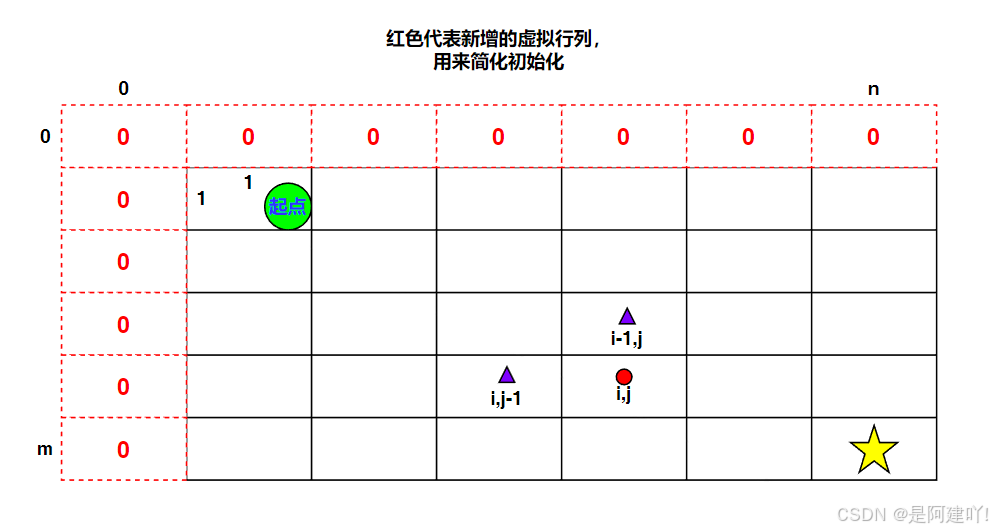
1. 状态表示：dp[i][j] 表示从左上角到达第 i 行第 j 列时能获得的最高珠宝总价值（对应矩阵中 frame[i-1][j-1]）
2. 状态转移方程 ：
   • 当前位置的最高价值由上方和左侧位置的最高价值推导而来：dp[i][j] = max(dp[i-1][j], dp[i][j-1]) + frame[i-1][j-1]
3. 初始化 ：
   • 定义 dp 数组初始值全为 0，dp[0][j] 和 dp[i][0] 默认为 0（虚拟的边界，代表网格外的位置，价值为 0），此设置确保：
     • 第一行（i=1）的位置只能从左侧移动到达，故 dp[1][j] = dp[1][j-1] + frame[0][j-1]
     • 第一列（j=1）的位置只能从上方移动到达，故 dp[i][1] = dp[i-1][1] + frame[i-1][0]
4. 填写 DP 表 ：
   • 从上到下遍历每一行，每一行从左到右遍历：
     • 外层循环从 i=1 遍历到 rows，内层循环从 j=1 遍历到 cols
     • 每个 dp[i][j] 都基于已计算的上方（dp[i-1][j]）和左侧（dp[i][j-1]）结果，确保子问题已先求解
5. 结果返回 ：
   • 右下角位置（rows-1, cols-1）的最高珠宝价值存储在 dp[rows][cols] 中，直接返回即可

编写代码：

class Solution {
public:
    int jewelleryValue(vector<vector<int>>& frame) {
        int rows = frame.size() , cols = frame[0].size();

        vector<vector<int>> dp(rows+1,vector<int>(cols+1,0));

        for(int i = 1 ; i <= rows ; i++)
        {
            for(int j = 1 ; j <= cols ; j++)
            {
                dp[i][j] = max(dp[i-1][j],dp[i][j-1]) + frame[i-1][j-1];
            }
        }

        return dp[rows][cols];
    }
};

---

四、下降路径最小和

题目描述：

思路讲解：

本道题需要我们找到整个矩阵的最小下降路径和，下降路径可从第一行任意元素开始，每行选择的元素需与上一行元素相邻（正下方或对角线左右），问题可拆解为：到达第 i 行第 j 列的最小路径和 = 上一行中可到达该位置的三个位置（j-1、j、j+1）的最小路径和 + 当前位置的元素值。下面的思路中添加了虚拟行列，为了方便初始化，以下是具体思路：

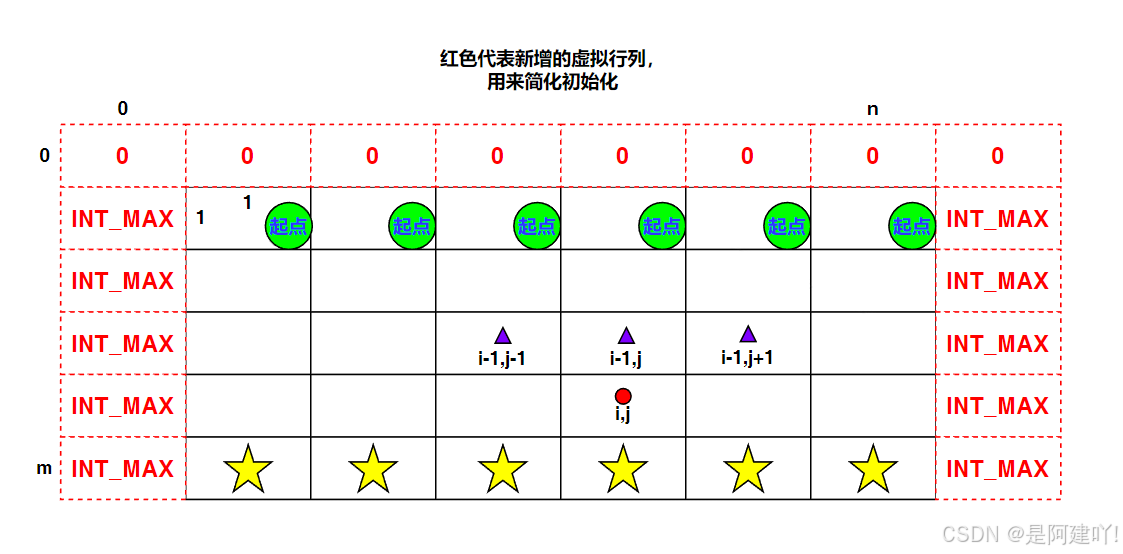
1. 状态表示：dp[i][j] 表示到达第 i 行第 j 列的最小下降路径和（对应矩阵中 matrix[i-1][j-1]）
2. 状态转移方程 ：
   • 当前位置的最小路径和由上一行三个可能位置的最小路径和推导而来：dp[i][j] = min(dp[i-1][j-1], min(dp[i-1][j], dp[i-1][j+1])) + matrix[i-1][j-1]
3. 初始化 ：
   • 定义 dp 数组为 (n+1) x (n+2) 大小，初始值为 INT_MAX，第一行、第一列和最后一列是虚拟行列，用来方便初始化
   • 第一行（i=0）的所有位置 dp[0][i] = 0（虚拟起始行），边界位置（如 j=1 或 j=n）所有位置为INT_MAX（虚拟列），此设置确保：
     • 第一行（i=1）的元素可直接从虚拟起始行获取路径和（dp[1][j] = 0 + matrix[0][j-1]）
     • 边界位置（如 j=1 或 j=n）的上一行相邻位置若超出范围（如 j-1=0 或 j+1=n+1），因初始值为 INT_MAX 会被自动排除，不影响最小值计算
4. 填写 DP 表 ：
   • 从上到下遍历每一行，每一行从左到右遍历：
     • 外层循环从 i=1 遍历到 i=n，内层循环从 j=1 遍历到 j=n
     • 每个 dp[i][j] 都基于已计算的上一行三个位置的结果，确保子问题已先求解
5. 结果返回 ：
   • 最后一行（i=n）的所有位置的最小路径和中，最小值即为整个矩阵的最小下降路径和，因此遍历 dp[n][1...n] 取最小值返回

编写代码：

class Solution {
public:
    int minFallingPathSum(vector<vector<int>>& matrix) {
        int n = matrix.size();

        vector<vector<int>> dp(n+1,vector<int>(n+2,INT_MAX));
        for(int i = 0 ; i <= n ; i++)
            dp[0][i] = 0;

        for(int i = 1 ; i <= n ; i++)
        {
            for(int j = 1 ; j <= n ; j++)
            {
                dp[i][j] = min(dp[i-1][j-1],min(dp[i-1][j],dp[i-1][j+1])) + matrix[i-1][j-1];
            }
        }

        int ret = INT_MAX;
        for(int i = 1 ; i <= n ; i++)
        {
            ret = min(ret,dp[n][i]);
        }

        return ret;
    }
};

---

五、最小路径和

题目描述：

思路讲解：

本道题需要我们找到路径上数字总和最小的路径，从左上角到右下角的路径中，每次只能向下或向右移动，问题可拆解为：到达（i,j）的最小路径和 = 到达上方（i-1,j）或左侧（i,j-1）的最小路径和（取较小者） + 当前位置的数字。下面的思路中添加了虚拟行列，为了方便初始化，以下为具体思路：

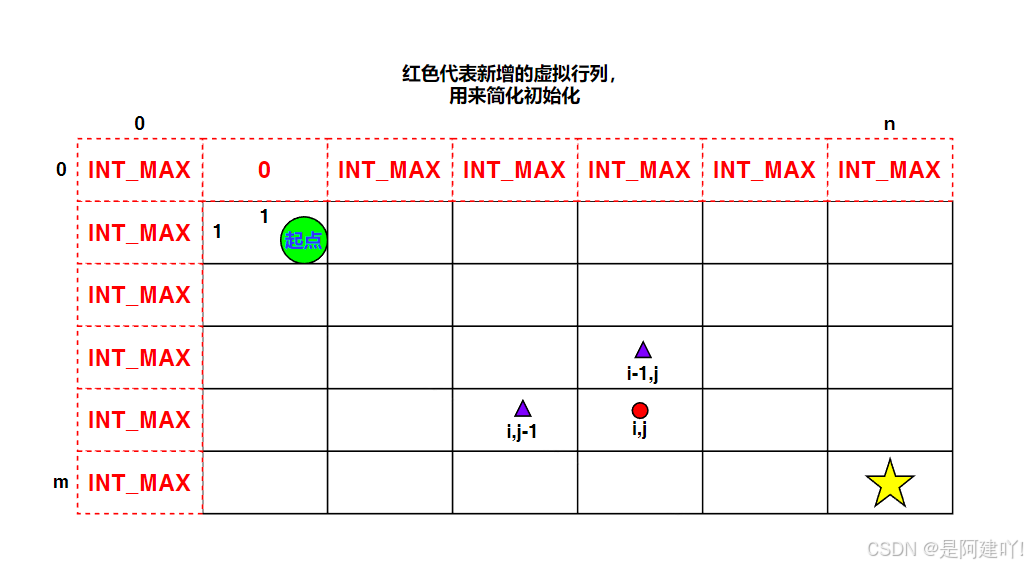
1. 状态表示：dp[i][j] 表示从左上角（0,0）到达第 i 行第 j 列的最小路径总和（对应矩阵中 grid[i-1][j-1]）
2. 状态转移方程 ：
   • 当前位置的最小路径和由上方和左侧位置的最小路径和推导而来：dp[i][j] = min(dp[i-1][j], dp[i][j-1]) + grid[i-1][j-1]
3. 初始化 ：
   • 定义 dp 数组为 (rows+1) x (cols+1) 大小，初始值为 INT_MAX
   • 特殊设置 dp[0][1] = 0（虚拟的起始点，位于左上角上方），作为路径计算的起点，此设置确保：
     • 第一行（i=1）的位置只能从左侧移动到达，因上方 dp[0][j] 除 dp[0][1] 外均为 INT_MAX，故 dp[1][j] = dp[1][j-1] + grid[0][j-1]
     • 第一列（j=1）的位置只能从上方移动到达，因左侧 dp[i][0] 为 INT_MAX，故 dp[i][1] = dp[i-1][1] + grid[i-1][0]
     • 起点（0,0）的路径和正确计算为 dp[1][1] = dp[0][1] + grid[0][0] = 0 + grid[0][0]
4. 填写 DP 表 ：
   • 从上到下遍历每一行，每一行从左到右遍历网格：
     • 外层循环从 i=1 遍历到 rows，内层循环从 j=1 遍历到 cols
     • 每个 dp[i][j] 都基于已计算的上方（dp[i-1][j]）和左侧（dp[i][j-1]）结果，确保子问题已先求解
5. 结果返回 ：
   • 右下角位置（rows-1, cols-1）的最小路径和存储在 dp[rows][cols] 中，直接返回即可

编写代码：

class Solution {
public:
    int minPathSum(vector<vector<int>>& grid) {
        int rows = grid.size() , cols = grid[0].size();

        vector<vector<int>> dp(rows+1,vector<int>(cols+1,INT_MAX));
        dp[0][1] = 0;

        for(int i = 1 ; i <= rows ; i++)
        {
            for(int j = 1 ; j <= cols ; j++)
            {
                dp[i][j] = min(dp[i-1][j] , dp[i][j-1]) + grid[i-1][j-1];
            }
        }

        return dp[rows][cols];
    }
};

---

六、地下城游戏

题目描述：

思路讲解：

本道题需要我们计算骑士能够拯救到公主所需的最低初始健康点数，骑士从左上角到右下角（拯救公主），每次只能向右或向下移动，需保证全程健康值 > 0。由于当前房间的健康需求依赖后续房间（需知道到达终点前的最低要求），因此采用从终点反推起点的方式，以下是具体思路：

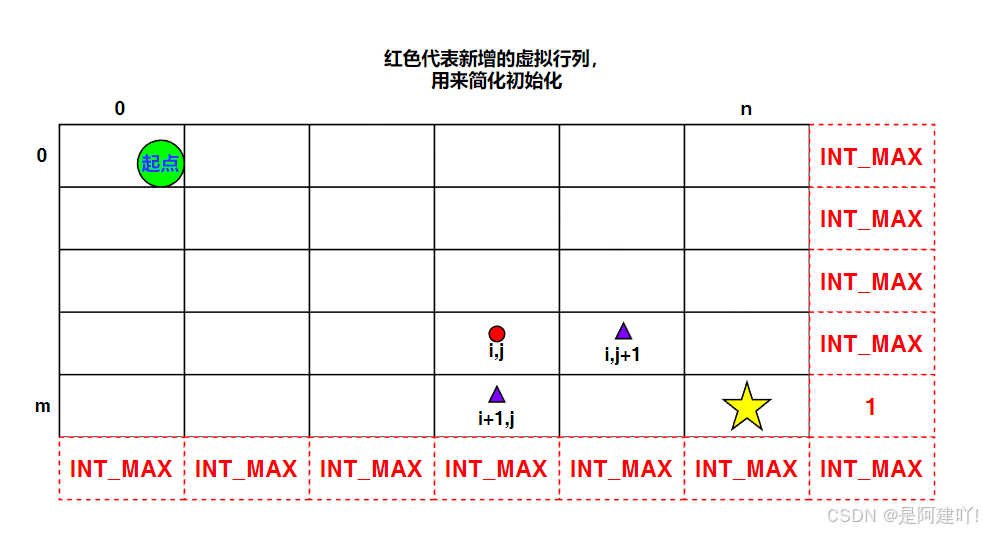
1. 状态表示：dp[i][j] 表示从房间 (i,j) 到达右下角所需的最小初始健康点数
2. 状态转移方程 ：
   • 对于房间 (i,j)，骑士可向右 (i,j+1) 或向下 (i+1,j) 移动，转移方程分两步：
     • 第一步：min(dp[i+1][j], dp[i][j+1]) - dungeon[i][j]
     • 表示从当前房间出发，选择向右或向下路径中健康需求较小的路径，减去当前房间的健康值变化
     • 第二步：max(1, 第一步结果)
     • 确保进入当前房间后的健康值至少为 1（健康值<=0 会死亡）
   • 最终转移方程：dp[i][j] = max(1, min(dp[i+1][j], dp[i][j+1]) - dungeon[i][j])
3. 初始化 ：
   • 定义 dp 数组为 (rows+1) x (cols+1) 大小，初始值为 INT_MAX
   • 特殊设置 dp[rows][cols-1] = 1：虚拟一个位于终点右侧的位置，作为反推的起点（到达终点后健康值至少为 1），此设置确保：
     • 终点 (rows-1, cols-1) 的计算正确：dp[rows-1][cols-1] = max(1, dp[rows][cols-1] - dungeon[rows-1][cols-1])
     • 最后一行（只能向右移动）和最后一列（只能向下移动）的边界处理简化，无需额外分支
4. 填写 DP 表 ：
   • 从下到上遍历每一行，每一行从右到左遍历：
     • 外层循环从 i = rows-1 向上遍历到 i=0
     • 内层循环从 j = cols-1 向左遍历到 j=0
     • 每个 dp[i][j] 都基于已计算的右侧（dp[i][j+1]）和下方（dp[i+1][j]）结果，确保后续路径的需求已先确定
5. 结果返回 ：
   • 起点 (0,0) 所需的最小初始健康点数存储在 dp[0][0] 中，直接返回即可

编写代码：

class Solution {
public:
    int calculateMinimumHP(vector<vector<int>>& dungeon) {
        int rows = dungeon.size() , cols = dungeon[0].size();

        vector<vector<int>> dp(rows+1,vector<int>(cols+1,INT_MAX));
        dp[rows][cols-1] = 1;

        for(int i = rows - 1 ; i >= 0 ; i--)
        {
            for(int j = cols - 1 ; j >= 0 ; j--)
            {
                dp[i][j] = min(dp[i+1][j] , dp[i][j+1]) - dungeon[i][j];
                dp[i][j] = max(1,dp[i][j]);
            }
        }

        return dp[0][0];
    }
};

---

结尾

如果有什么建议和疑问，或是有什么错误，大家可以在评论区中提出。

希望大家以后也能和我一起进步！！🌹🌹

如果这篇文章对你有用的话，希望大家给一个三连支持一下！！🌹🌹