一、岭回归算法
1、概述
-
岭回归(Ridge Regression)是一种线性回归技术,它通过在损失函数中加入一个正则化项来解决多重共线性问题。岭回归在普通最小二乘法的基础上添加了一个 L2 范数惩罚项,这样可以减小模型的方差,从而提高模型的泛化能力
-
损失函数公式:
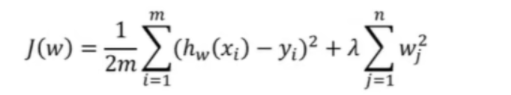
-
优点:
-
系数收缩:相比于最小二乘法,岭回归的回归系数倾向于更小,但不会被精确地收缩到零
-
防止过拟合:通过限制回归系数的大小,岭回归能够减少模型对训练数据的过拟合,提高了模型的泛化能力
-
处理多重共线性:在存在高度相关自变量的情况下,传统的最小二乘法可能会导致回归系数不稳定或者过大。岭回归通过引入正则化项(L2惩罚项)来减小这种不稳定性和过大的问题
-
2、API
-
sklearn.linear_model.Ridge()是 sklearn 提供的实现岭回归的一个模型,参数如下:-
alpha:default=1.0,正则项力度,也就是\\lambda的值
-
fit_intercept:default=True,是否计算偏置
-
solver:指定用于拟合系数的方法,{'auto', 'svd', 'cholesky', 'lsqr', 'sparse_cg', 'sag', 'saga', 'lbfgs'},default='auto'
-
normalize:default=True,数据进行标准化,如果特征工程中已经做过标准化,这里就该设置为False
-
max_iter:梯度解算器的最大迭代次数
-
案例:
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.linear_model import Ridge
from sklearn.metrics import mean_squared_error, r2_score
from sklearn.preprocessing import StandardScaler
# 加载波士顿房价数据集
boston = datasets.load_boston()
X = boston.data
y = boston.target
# 划分数据集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# 特征工程-标准化
transfer = StandardScaler()
X_train = transfer.fit_transform(X_train)
X_test = transfer.fit_transform(X_test)
# 创建岭回归模型
model = Ridge(alpha=0.5, fit_intercept=True, solver='auto', max_iter=10000)
# 训练模型
model.fit(X_train, y_train)
# 预测
y_pred = model.predict(X_test)
# 评估模型
mse = mean_squared_error(y_test, y_pred)
r2 = r2_score(y_test, y_pred)
# 输出结果
print('均方误差:', mse)
print('决定系数:', r2)
print('模型得分:', model.score(X_test, y_test))
print('模型系数:', model.coef_)
print('模型截距:', model.intercept_)二.拉索回归Lasso
1.1 损失函数公式
Lasso回归是一种线性回归模型,它通过添加所有权重的绝对值之和(L1)来惩罚模型的复杂度。
Lasso回归的目标是最小化以下损失函数:
\\text{J(w)}= \\frac{1}{2n}\\sum*{i=1}\^n (h_w(x_i)-y_i)\^2 + \\lambda \\sum*{j=1}\^p \|w_j\|
其中:
-
n 是样本数量,
-
p 是特征的数量,
-
y_i 是第 i 个样本的目标值,
-
x_i 是第 i 个样本的特征向量,
-
w是模型的参数向量,
-
\\lambda 是正则化参数,控制正则化项的强度。
特点:
-
拉索回归可以将一些权重压缩到零,从而实现特征选择。这意味着模型最终可能只包含一部分特征。
-
适用于特征数量远大于样本数量的情况,或者当特征间存在相关性时,可以从中选择最相关的特征。
-
拉索回归产生的模型可能更简单,因为它会去除一些不重要的特征。
1.2 API
sklearn.linear_model.Lasso()
参数:
-
alpha (float, default=1.0):
- 控制正则化强度;必须是非负浮点数。较大的 alpha 增加了正则化强度。
-
fit_intercept (bool, default=True):
- 是否计算此模型的截距。如果设置为 False,则不会使用截距(即数据应该已经被居中)。
-
precompute (bool or array-like, default=False):
- 如果为 True,则使用预计算的 Gram 矩阵来加速计算。如果为数组,则使用提供的 Gram 矩阵。
-
copy_X (bool, default=True):
- 如果为 True,则复制数据 X,否则可能对其进行修改。
-
max_iter (int, default=1000):
- 最大迭代次数。
-
tol (float, default=1e-4):
- 精度阈值。如果更新后的系数向量减去之前的系数向量的无穷范数除以 1 加上更新后的系数向量的无穷范数小于 tol,则认为收敛。
-
warm_start (bool, default=False):
- 当设置为 True 时,再次调用 fit 方法会重新使用之前调用 fit 方法的结果作为初始估计值,而不是清零它们。
-
positive (bool, default=False):
- 当设置为 True 时,强制系数为非负。
-
random_state (int, RandomState instance, default=None):
- 随机数生成器的状态。用于随机初始化坐标下降算法中的随机选择。
-
selection ({'cyclic', 'random'}, default='cyclic'):
- 如果设置为 'random',则随机选择坐标进行更新。如果设置为 'cyclic',则按照循环顺序选择坐标。
属性:
-
coef_
- 系数向量或者矩阵,代表了每个特征的权重。
-
intercept_
- 截距项(如果 fit_intercept=True)。
-
n_iter_
- 实际使用的迭代次数。
-
n_features_in_ (int):
- 训练样本中特征的数量。
1.3 示例
from sklearn.datasets import fetch_california_housing
from sklearn.linear_model import Lasso
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error
import numpy as np
# 加载波士顿房价数据集
data = fetch_california_housing(data_home="./src")
X, y = data.data, data.target
# 划分训练集和测试集
X_train, x_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# 创建Lasso回归模型
lasso = Lasso(alpha=0.1) # alpha是正则化参数
# 训练模型
lasso.fit(X_train, y_train)
# 得出模型
print("权重系数为:\n", lasso.coef_) #权重系数与特征数一定是同样的个数。
print("偏置为:\n", lasso.intercept_)
#模型评估
y_predict = lasso.predict(x_test)
print("预测的数据集:\n", y_predict)
error = mean_squared_error(y_test, y_predict)
print("均方误差为:\n", error)