leetcode 3195 包含1的最小矩形面积

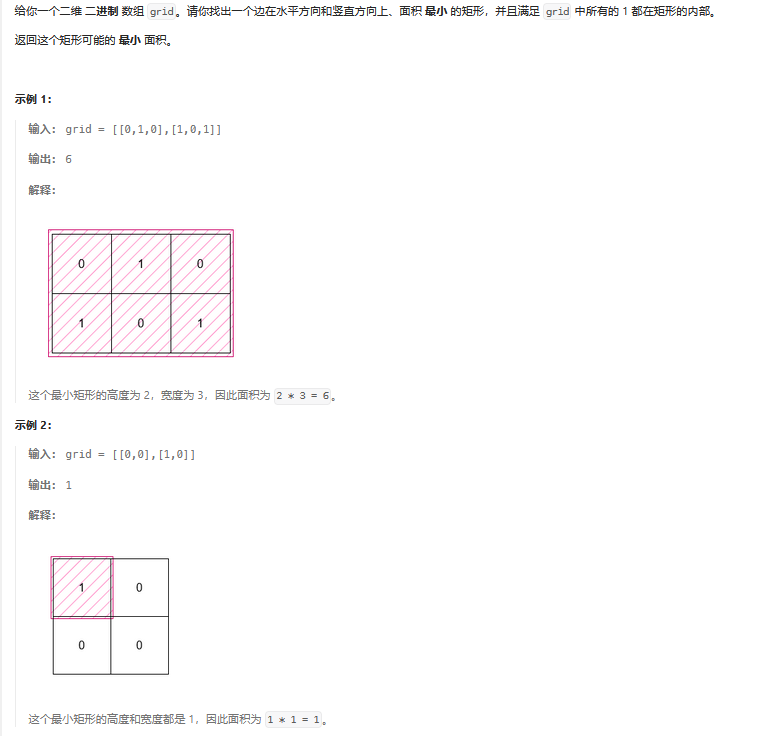
一、题目描述

二、解题思路

(1)定义布尔向量row和line分别用于统计每列(竖向)和每行(横向)是否出现1，初始化为false；

(2)如果出现了1就将相应的布尔值设置为true；

(3)然后别对得到的两个向量使用双指针求解矩阵的长与宽，长乘以宽即为面积；

三、代码实现

解法一：

时间复杂度：T(n)=O(n^2)

空间复杂度：S(n)O(n)

cpp 复制代码

class Solution {
public:
    int minimumArea(vector<vector<int>>& grid) {
        //逆向双指针
        //边界处理
        if(grid.empty()&!grid[0].empty()) return 0;
        //行
        vector<bool> row(grid[0].size(),false);
        for(int i=0;i!=grid[0].size();i++)
            for(int j=0;j!=grid.size();j++)
                if(grid[j][i]==1){
                     row[i]=true;
                     break;
                }
        int left1=0,right1=row.size()-1;
        while(row[left1]==false&&left1<=right1) left1++;     
        while(row[right1]==false&&left1<=right1) right1--;
        int Long=right1-left1+1;

        //列
        vector<bool> line(grid.size(),false);
        for(int i=0;i!=grid.size();i++)
            for(int j=0;j!=grid[0].size();j++)
                if(grid[i][j]==1){
                    line[i]=true;
                    break;
                }
        int left2=0,right2=line.size()-1;
        while(line[left2]==0&&left2<=right2) left2++;
        while(line[right2]==0&&left2<=right2)right2--;
        int Hight=right2-left2+1;
        return Long*Hight;
    }
};

**解法二：**定义up、down、left、right四个变量，遍历数组，按要求更新四个变量(逐步扩大)，最后求得满足条件的最小矩形的面积。

时间复杂度：T(n)=O(n^2)

空间复杂度：S(n)=O(1)

cpp 复制代码

class Solution {
public:
    int minimumArea(vector<vector<int>>& grid) {
        //边界处理
        if(grid.empty()||grid[0].empty()) return 0;
        //逐步扩大矩形直至满足题目条件
        int m=grid[0].size(),n=grid.size();
        int up=n,down=0,left=m,right=0;
        for(int i=0;i!=n;i++)
            for(int j=0;j!=m;j++)
                if(grid[i][j]==1){
                    if(i<left) left=i;
                    if(i>right) right=i;
                    if(j<up) up=j;
                    if(j>down) down=j;
                }
        return (right-left+1)*(down-up+1);
    }
};