A 小苯的方格覆盖

思路:
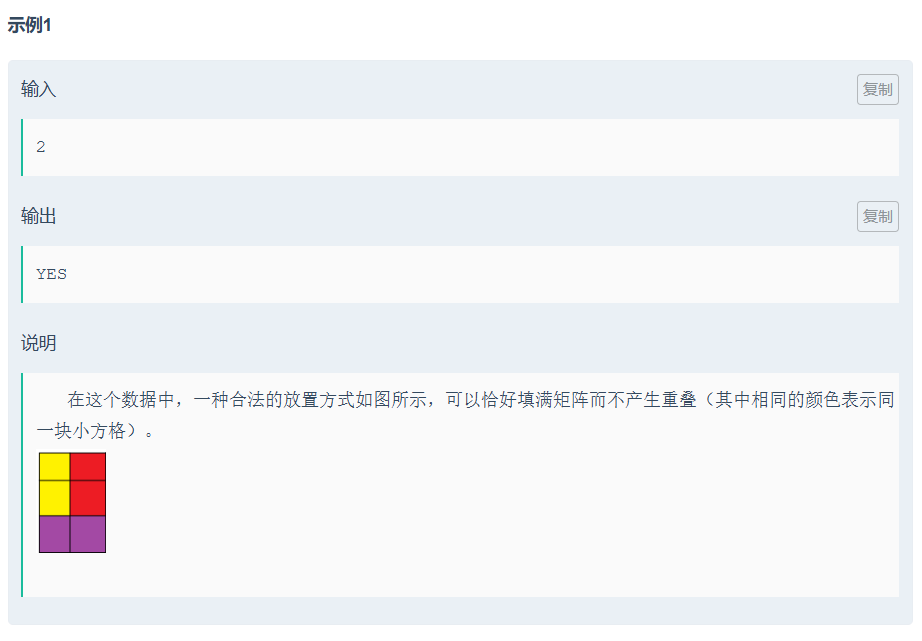
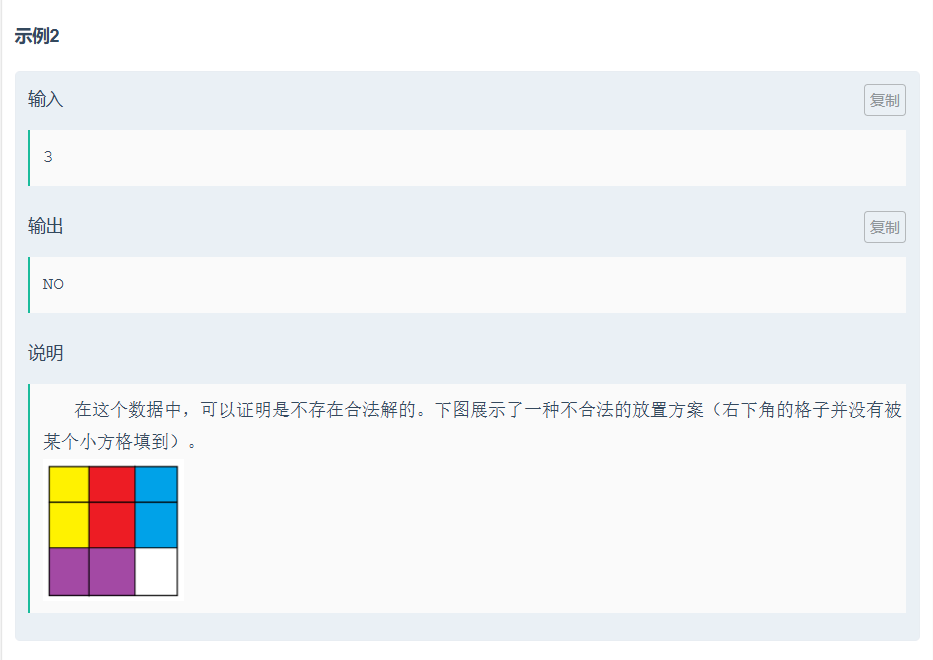
怎么摆第三行都是横放的2*1;
故若n为奇数,总格子数3n为奇数,无法被2整除,直接排除。
cpp
#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
#include<iostream>
#include<bits/stdc++.h>
#define ll long long
using namespace std;
int main(){
ios::sync_with_stdio(false); // 禁用同步
cin.tie(nullptr); // 解除cin与cout绑定
int n;
cin >> n;
if (n % 2 == 0) {
cout << "YES" << endl;
}
else
cout << "NO" << endl;
return 0;
}B 小苯的数字折叠


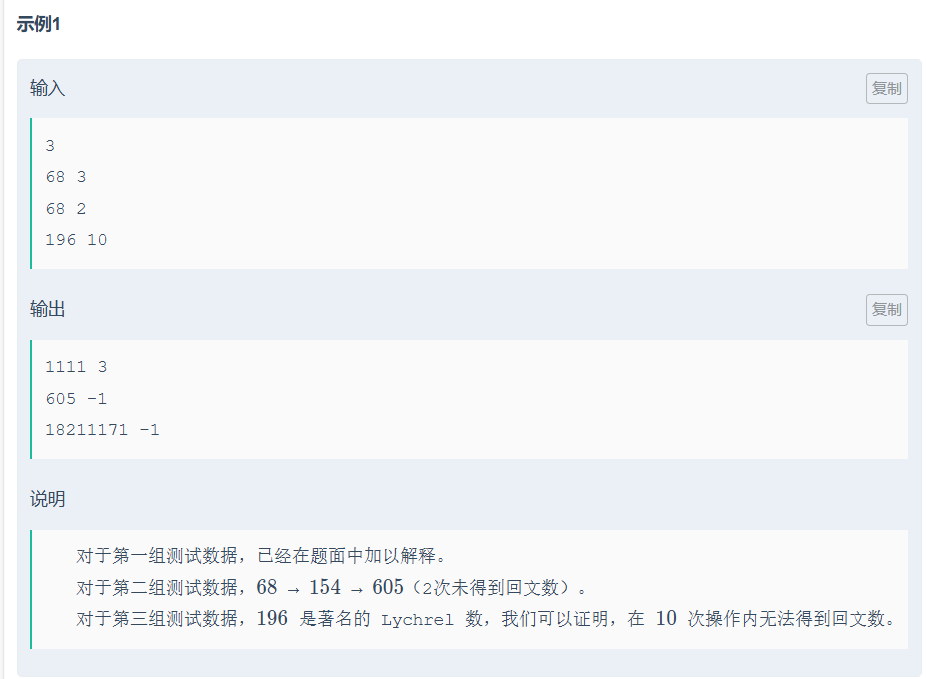
思路:暴力+判断
cpp
#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
#include<iostream>
#include<bits/stdc++.h>
#define ll long long
using namespace std;
int main(){
ios::sync_with_stdio(false); // 禁用同步
cin.tie(nullptr); // 解除cin与cout绑定
ll t;
cin >> t;
while(t--){
ll n, k;
cin >> n >> k;
ll i;
bool pan1 = false;
for (i = 0; i <= k; i++) {
bool pan = true;
vector<ll> a;
ll w = n;
while (w > 0) {
a.push_back(w % 10);
w /= 10;
}
ll pp = a.size();
for (ll j = 0; j < pp; j++) {
if (a[j] != a[pp - 1 - j]) {
pan = false;
break;
}
}
if (pan) {
pan1 = true;
break;
}
if (i >= k) {
break;
}
ll q = 1;
ll j = pp - 1;
while (a[j] == 0&&j>=0) {
j--;
}
for ( ; j >=0; j--) {
n += a[j] * q;
q *= 10;
}
}
if (!pan1) {
cout << n <<" " << -1 << endl;
}
else {
cout << n << " " << i << endl;
}
}
return 0;
}C 小苯的波浪加密器

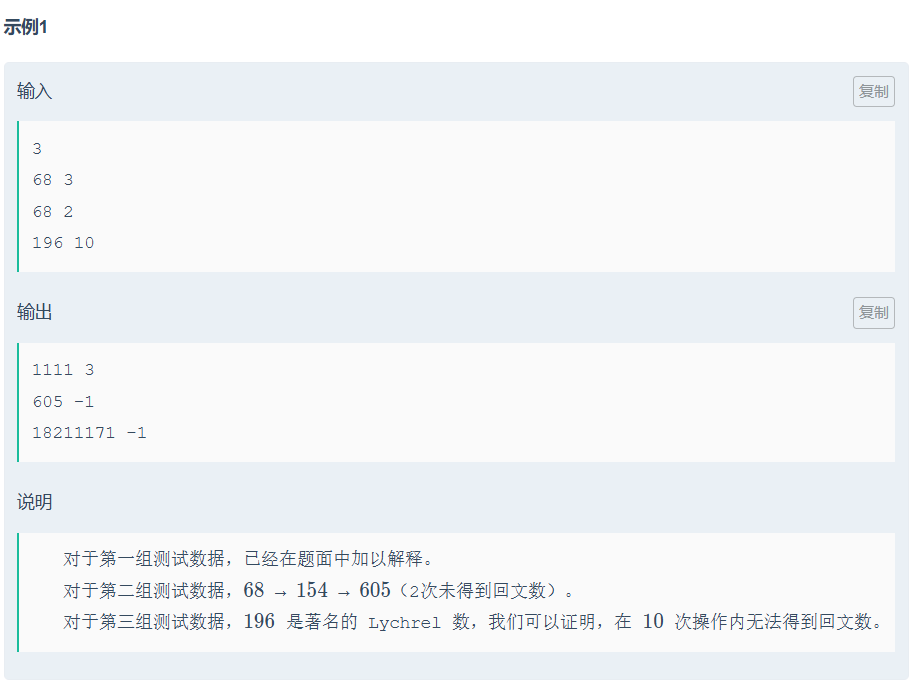
思路:
只要明白个位=个位*个位%10
所以范围为:,暴力
但要考虑n==3时,a[4] 不存在
cpp
#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
#include<iostream>
#include<bits/stdc++.h>
#define ll long long
using namespace std;
int main(){
ios::sync_with_stdio(false); // 禁用同步
cin.tie(nullptr); // 解除cin与cout绑定
ll t;
cin >> t;
while(t--)
{
ll n, l1, l2, r1, r2;
cin >> n >> l1 >> r1 >> l2 >> r2;
r1 = min(r1, l1 + 9);
r2 = min(r2, l2 + 9);
vector<ll >a(n + 1);
for (ll i = 3; i <= n; i++) {
cin >> a[i];
}
ll i, j;
for (i = l1; i <= r1; i++) {
bool pan = false;
for (j = l2; j <= r2; j++) {
if ((i % 10) * (j % 10) % 10 == a[3] && (n==3||(j % 10) * a[3] % 10 == a[4])) {
pan = true;
break;
}
}
if (pan) {
break;
}
}
if (i > r1) {
cout << -1 << " " << -1 << endl;
}
else {
cout << i << " " << j << endl;
}
}
return 0;
}D 小苯的数字变换

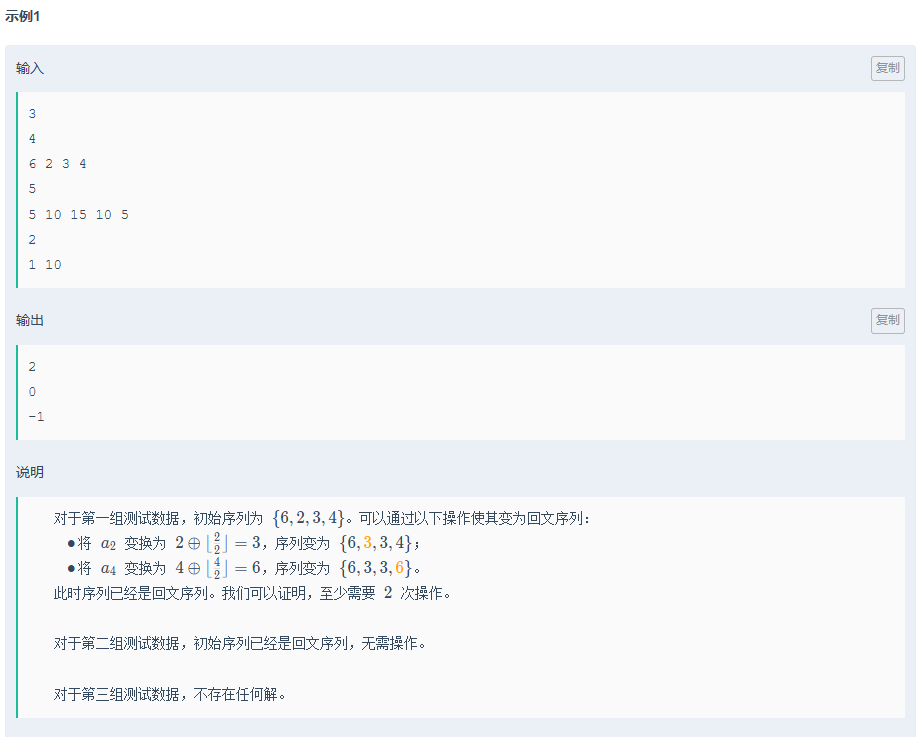
思路:
多列几个数就可以发现 会循环(看别人说是log(n)级别)
然后有两种:
一:将 a[i],和a[n +1- i]同时变换并记录,讨论每种情况;
二:将a[i] 遍历循环一次,看有没有a[n +1- i],然后min(k,u-k);k为第几次出现,u为循环数有几个
(或直接循环两次或x,y都循环一次)
**方法一:**不推荐
cpp
#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
#include<iostream>
#include<bits/stdc++.h>
#define ll long long
using namespace std;
int t, n;
int qwe(int i, int j) {
if (i == j) {
return 0;
}
map<int, int> l, r;
l.insert({ i,0 });
r.insert({ j,0 });
int u = 1;
int min_sum = INT_MAX;
while (1) {
bool pan = true;
if (l.find(i ^ (i / 2))==l.end()) {
pan = false;
i = i ^ (i / 2);
l.insert({i,u});
auto it = r.find(i);
if (it == r.end()) {
}
else {
min_sum = min(min_sum, u + it->second);
}
}
if (r.find(j ^ (j / 2))==r.end()) {
pan = false;
j = j ^ (j / 2);
r.insert({ j,u });
auto it = l.find(j);
if (it == l.end()) {
}
else {
min_sum = min(min_sum, u + it->second);
}
}
u++;
if (pan) {
break;
}
}
return min_sum == INT_MAX ? -1 : min_sum;
}
int main(){
ios::sync_with_stdio(false); // 禁用同步
cin.tie(nullptr); // 解除cin与cout绑定
cin >> t;
while(t--){
cin >> n;
vector<int> a(n + 1);
for (int i = 1; i <= n; i++) {
cin >> a[i];
}
int i;
ll sum = 0;
for ( i = 1; i <= n/2; i++) {
int y = qwe(a[i], a[n +1- i]);
if (y == -1) {
break;
}
else {
sum += y;
}
}
if (i <= n / 2) {
cout << -1 << endl;
}
else
cout << sum << endl;
}
return 0;
}方法二:
cpp
#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
#include<iostream>
#include<bits/stdc++.h>
#define ll long long
using namespace std;
int N = 5e5 + 10;
ll ans[N];
ll n;
ll tsf(ll x, ll y){
ll sum = 0;
while(x != y){
if(sum > 32) return -1;
x = (x ^ (x / 2));
sum++;
}
return sum;
}
void solve()
{
cin >> n;
for(int i = 1; i <= n; i++) cin >> ans[i];
ll tot = 0;
for(int i = 1; i <= n / 2; i++) {
if(ans[i] == ans[n - i + 1]) continue;
ll x = tsf(ans[i], ans[n - i + 1]),y = tsf(ans[n - i + 1], ans[i]);
if(x == -1 || y == -1){
cout << -1 << endl;
return ;
}
tot += min(x,y);
}
cout << tot << endl;
}
int main()
{
ll t = 1;
cin >> t;
while (t--)
{
solve();
}
}E 小苯的洞数组构造

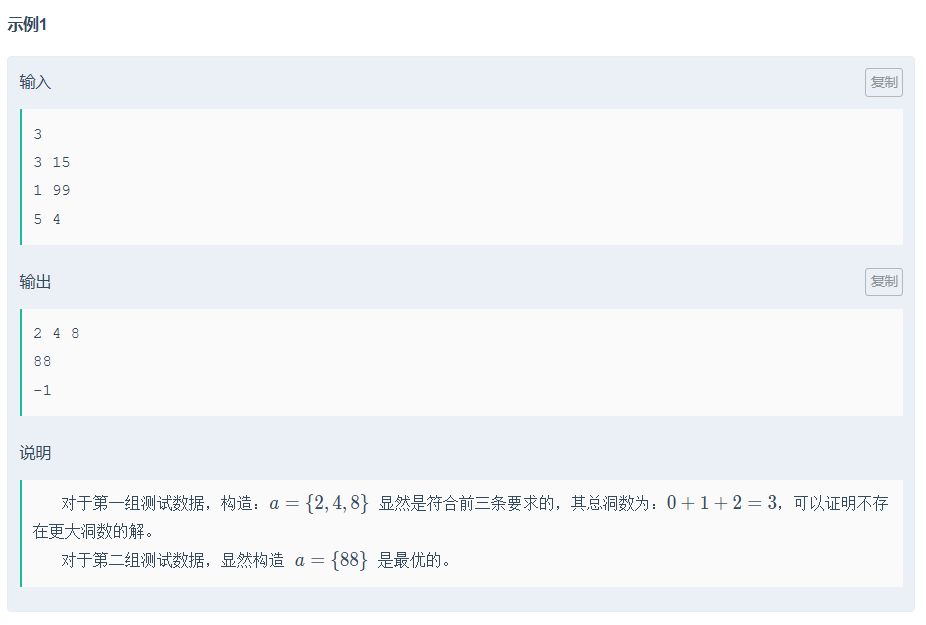
思路:贪心
最大化洞数 数字8的洞数为2,是单个数字中洞数最大的。因此,尽可能多地使用数字8可以最大化洞数之和。构造全8的数字(如8, 88, 888等)可以高效地实现这一点,其次是4;
分配策略 为了确保总和不超过sum,需要合理分配数字的大小。通过计算平均每个数字的最大值x,可以确定使用多少位的全8数字。如果x足够大,直接使用全8数字;否则,调整数字范围,确保总和不超过sum。
边界处理 当sum<n时,无法满足每个数字至少为1的条件,直接输出-1。其他情况下,通过动态调整每个数字的大小,确保总和不超过sum的同时最大化洞数之和。
cpp
#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
#include<iostream>
#include<bits/stdc++.h>
#define ll long long
using namespace std;
ll t, n, sum;
ll a[11];
ll shu(ll i) {
ll j = 0;
while (i > 0) {
j++;
i /= 10;
}
return j;
}
void solve() {
cin >> n >> sum;
if (sum < n) {
cout << -1 << endl;
return;
}
ll l, r;
ll x = sum / n;
ll y = shu(x);
ll o = a[y] + 4 * pow(10, y);
if (x >= a[y]) {
l = a[y], r = o;
}
else if(x>=o/10){
l = o / 10; r = a[y];
}
else {
l = a[y - 1], r = o / 10;
}
for (int i = 0; i < n; i++) {
if (sum / (n - i) >= r) {
cout << r << " ";
sum -= r;
}
else {
cout << l << " ";
sum -= l;
}
}
cout << endl;
return;
}
int main(){
ios::sync_with_stdio(false); // 禁用同步
cin.tie(nullptr); // 解除cin与cout绑定
cin >> t;
for (int i = 1; i <= 10; i++) {
a[i] = a[i - 1] * 10 + 8;
}
a[0] = 1;
while(t--){
solve();
}
return 0;
}F 小苯的数组计数

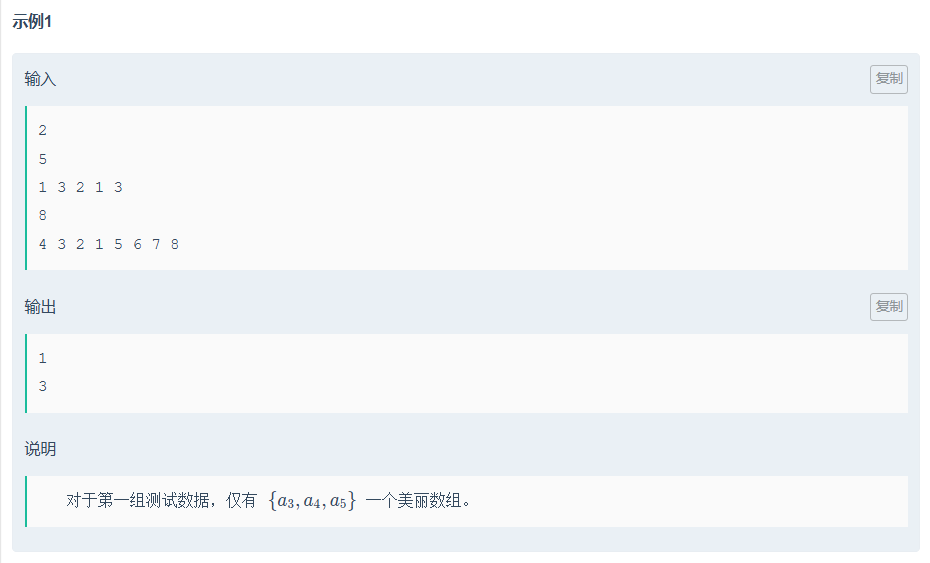
思路: 单调栈
核心思路是利用单调栈分别从左到右和从右到左遍历数组,统计满足条件的子数组。
- 单调栈预处理:从左到右遍历数组,维护一个单调递减栈,记录每个元素左边最近的比它大的元素位置。(左小于右)
- 统计条件满足的子数组:在遍历过程中,如果当前元素与栈顶元素的位置差 ≥ 2且值不相等,则说明存在满足条件的子数组。
- 反向遍历:从右到左重复相同操作,确保覆盖所有可能的子数组情况。
- 去重处理:避免重复计数,确保每个子数组只被统计一次。(右小于左)
cpp
#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
#include<iostream>
#include<bits/stdc++.h>
#define ll long long
using namespace std;
int t, n;
int main(){
ios::sync_with_stdio(false); // 禁用同步
cin.tie(nullptr); // 解除cin与cout绑定
cin >> t;
while(t--){
cin >> n;
vector<int> a(n);
for (int i = 0; i < n; i++) {
cin >> a[i];
}
stack<int> q;
ll sum = 0;
for (int i = 0; i < n; i++) {
while (!q.empty() && a[i] > a[q.top()]) {
q.pop();
}
if (!q.empty() && i - q.top() >= 2&&a[i]!=a[q.top()]) {
sum++;
}
q.push(i);
}
while (!q.empty()) {
q.pop();
}
for (int i = n-1; i >=0; i--) {
while (!q.empty() && a[i] > a[q.top()]) {
q.pop();
}
if (!q.empty() && q.top()-i >= 2 && a[i] != a[q.top()]) {
sum++;
}
q.push(i);
}
cout << sum << endl;
}
return 0;
}