5.1 Twelve ways to fool the masses
5.1 愚弄大众的十二种方法
5.2.1 Prelim: Old MacDonald meets Lagrange
5.2.1 前言:老麦克唐纳遇见拉格朗日
5.2. Prelim: Meet stubborn vectors
5.2. 前言:遇见顽固向量
5.2.3 Prelim: Covariance and its friends
5.2.3 前言:协方差及其相关概念
PCA技术前言
- 矩阵作为运算符
- [特征向量 Eigen Vectors](#特征向量 Eigen Vectors)
- [Mean 均值](#Mean 均值)
- Variance方差
- 协方差 (Co-Variance)
- Correlation相关性
矩阵作为运算符
向量与矩阵的乘法可以看作是向量的几何变换
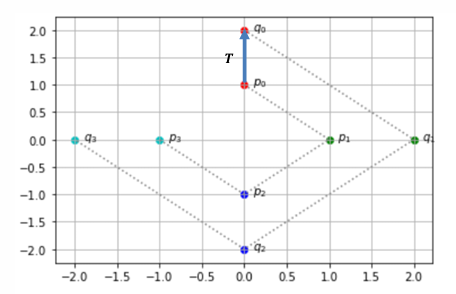
点(0,1)经过矩阵乘法变换到点(0,2),所以矩阵乘法可以看作对向量的一个变换。
T = [ 2 0 0 2 ] , x = [ 0 1 ] T = \begin{bmatrix} 2 & 0 \\ 0 & 2 \end{bmatrix}, \quad x = \begin{bmatrix} 0 \\ 1 \end{bmatrix} T=[2002],x=[01]
y = T x = [ 0 2 ] y = Tx = \begin{bmatrix} 0 \\ 2 \end{bmatrix} y=Tx=[02]
特征向量 Eigen Vectors
对于一个给定的矩阵,那些仅仅发生尺度变化(长度改变而方向不变)的特征点称为 特征向量(Eigen vectors)
T v = λ v Tv = \lambda v Tv=λv
v = 特征向量,方向不变的特殊向量
λ = 特征值,缩放倍数
T = 执行变换的矩阵
本质:矩阵作用导致缩放,方向不改变
如何求解它们:
由
( T − λ I ) v = 0 (T - \lambda I)v = 0 (T−λI)v=0
可推出
∣ T − λ I ∣ = 0 |T - \lambda I| = 0 ∣T−λI∣=0
示例
给定矩阵,
T = [ 3 1 0 2 ] T = \begin{bmatrix} 3 & 1 \\ 0 & 2 \end{bmatrix} T=[3012]
特征向量一 (Eigen Vector) :
1 0 \] , 特征值 (Eigen Value) = 3 \\begin{bmatrix} 1 \\\\ 0 \\end{bmatrix}, \\quad \\text{特征值 (Eigen Value)} = 3 \[10\],特征值 (Eigen Value)=3 验证: , \[ 3 1 0 2 \] \[ 1 0 \] = \[ 3 0 \] = 3 \[ 1 0 \] \\begin{bmatrix} 3 \& 1 \\\\0 \& 2\\end{bmatrix}\\begin{bmatrix}1 \\\\ 0 \\end{bmatrix} =\\begin{bmatrix} 3 \\\\ 0 \\end{bmatrix} = 3 \\begin{bmatrix} 1 \\\\ 0 \\end{bmatrix} \[3012\]\[10\]=\[30\]=3\[10
说明:这里只是 缩放 (scaling),导致放大3倍,方向不变。

特征向量二 (Eigen Vector):
− 0.707 0.707 \] , 特征值 (Eigen Value) = 2 \\begin{bmatrix} -0.707 \\\\ 0.707 \\end{bmatrix}, \\quad \\text{特征值 (Eigen Value)} = 2 \[−0.7070.707\],特征值 (Eigen Value)=2 验证: \[ 3 1 0 2 \] \[ − 0.707 0.707 \] = \[ − 1.414 1.414 \] = 2 \[ − 0.707 0.707 \] \\begin{bmatrix} 3 \& 1 \\\\ 0 \& 2 \\end{bmatrix} \\begin{bmatrix} -0.707 \\\\ 0.707\\end{bmatrix}= \\begin{bmatrix} -1.414 \\\\ 1.414 \\end{bmatrix}= 2 \\begin{bmatrix} -0.707 \\\\ 0.707 \\end{bmatrix} \[3012\]\[−0.7070.707\]=\[−1.4141.414\]=2\[−0.7070.707
说明:该向量在矩阵作用下,被放大了 2 倍,方向保持不变。
Mean 均值
均值是给定变量的期望值 (expected value)
均值:求平均值,总值除以个数
基础形式
μ z = 1 N ∑ i = 1 N z i \mu_z = \frac{1}{N} \sum_{i=1}^N z_i μz=N1i=1∑Nzi
向量形式
z = [ z 1 , z 2 , ... , z N ] T z = [z_1, z_2, \dots, z_N]^T z=[z1,z2,...,zN]T
μ Z = 1 N ∑ i = 1 N z i = 1 N z T 1 \mu_Z = \frac{1}{N} \sum_{i=1}^N z_i = \frac{1}{N} z^T \mathbf{1} μZ=N1i=1∑Nzi=N1zT1
其中, 1 \mathbf{1} 1 表示元素全为 1 的向量。
概率形式
均值是变量的一阶矩 (first order moment),也可以写作期望值:
E [ z ] = ∑ i z i p Z ( z i ) E[z] = \sum_i z_i p_Z(z_i) E[z]=i∑zipZ(zi)
其中:
- z i z_i zi = 取值 (value)
- p Z ( z i ) p_Z(z_i) pZ(zi) = 该值出现的频率或概率 (Fraction of the time / probability)
示例 (Example)
假设掷骰子 10 次,得到的数值序列为:
1 , 1 , 2 , 3 , 3 , 4 , 4 , 5 , 6 , 6 1, 1, 2, 3, 3, 4, 4, 5, 6, 6 1,1,2,3,3,4,4,5,6,6
则平均值为:
1 ⋅ 2 10 + 2 ⋅ 1 10 + 3 ⋅ 2 10 + 4 ⋅ 2 10 + 5 ⋅ 1 10 + 6 ⋅ 2 10 = 3.5 1 \cdot \frac{2}{10} + 2 \cdot \frac{1}{10} + 3 \cdot \frac{2}{10} + 4 \cdot \frac{2}{10} + 5 \cdot \frac{1}{10} + 6 \cdot \frac{2}{10} = 3.5 1⋅102+2⋅101+3⋅102+4⋅102+5⋅101+6⋅102=3.5
Variance方差
方差:每个数值减去均值后的平方,相加的和,除以个数
v a r ( x ) = 1 N ∑ i = 1 N ( x i − μ ) 2 \color{red}{var(x) = \frac{1}{N} \sum_{i=1}^N (x_i - \mu)^2} var(x)=N1i=1∑N(xi−μ)2
其中:
- x i x_i xi 表示第 i i i 个数据点
- μ \mu μ 表示样本的均值
- N N N 表示数据点的个数
一旦我们计算了样本均值,其中一个数据点就不再是自由变化的,因此自由度减少 1,这就是 贝塞尔校正 (Bessel Correction) 的来源:
v a r ( z ) = 1 N − 1 ∑ i = 1 N ( z i − μ z ) 2 = 1 N − 1 ( z − μ z ) T ( z − μ z ) var(z) = \frac{1}{N-1} \sum_{i=1}^N (z_i - \mu_z)^2 = \frac{1}{N-1} (z - \mu_z)^T (z - \mu_z) var(z)=N−11i=1∑N(zi−μz)2=N−11(z−μz)T(z−μz)
如果均值为 0,那么方差公式可以简化为:
v a r ( z ) = 1 N z T z = 1 N ∥ z ∥ 2 var(z) = \frac{1}{N} z^T z = \frac{1}{N} \|z\|^2 var(z)=N1zTz=N1∥z∥2
方差也可以表示为期望形式:
v a r ( z ) = E [ ( z − μ z ) 2 ] var(z) = E \Big[ (z - \mu_z)^2 \Big] var(z)=E[(z−μz)2]
协方差 (Co-Variance)
对于两个随机变量,它们之间线性相关的程度由协方差来衡量。
协方差公式
c o v ( x , y ) = 1 N ∑ i = 1 N ( x i − μ x ) ( y i − μ y ) = 1 N ( x − μ x ) T ( y − μ y ) \color{red}cov(x,y) = \frac{1}{N} \sum_{i=1}^N (x_i - \mu_x)(y_i - \mu_y) = \frac{1}{N} (x - \mu_x)^T (y - \mu_y) cov(x,y)=N1i=1∑N(xi−μx)(yi−μy)=N1(x−μx)T(y−μy)
其中:
- x , y x, y x,y 是两个随机变量的取值向量
- μ x , μ y \mu_x, \mu_y μx,μy 分别是 x , y x, y x,y 的均值
如果两个变量的均值为零:
c o v ( x , y ) = 1 N x T y cov(x,y) = \frac{1}{N} x^T y cov(x,y)=N1xTy
此时,当两个向量共线或平行时,协方差最大。
期望形式表示
c o v ( x , y ) = E [ ( y − μ y ) ( x − μ x ) ] cov(x,y) = E \Big[ (y - \mu_y)(x - \mu_x) \Big] cov(x,y)=E[(y−μy)(x−μx)]
与方差的关系
当 x = y = z x=y=z x=y=z 时:
v a r ( z ) = c o v ( z , z ) var(z) = cov(z,z) var(z)=cov(z,z)
当x=y时,方差等于协方差。
协方差矩阵 (Covariance Matrix)
对于随机向量:
X = [ X 1 X 2 ⋮ X d ] X = \begin{bmatrix} X_1 \\ X_2 \\ \vdots \\ X_d \end{bmatrix} X= X1X2⋮Xd
协方差矩阵定义为:
Σ = C o v ( X , X ) = E [ ( X − μ ) ( X − μ ) T ] \Sigma = Cov(X,X) = E\big[(X - \mu)(X - \mu)^T\big] Σ=Cov(X,X)=E[(X−μ)(X−μ)T]
展开形式:
Σ = [ V a r ( X 1 ) C o v ( X 1 , X 2 ) ⋯ C o v ( X 1 , X d ) C o v ( X 2 , X 1 ) V a r ( X 2 ) ⋯ C o v ( X 2 , X d ) ⋮ ⋮ ⋱ ⋮ C o v ( X d , X 1 ) C o v ( X d , X 2 ) ⋯ V a r ( X d ) ] \Sigma = \begin{bmatrix} Var(X_1) & Cov(X_1,X_2) & \cdots & Cov(X_1,X_d) \\ Cov(X_2,X_1) & Var(X_2) & \cdots & Cov(X_2,X_d) \\ \vdots & \vdots & \ddots & \vdots \\ Cov(X_d,X_1) & Cov(X_d,X_2) & \cdots & Var(X_d) \end{bmatrix} Σ= Var(X1)Cov(X2,X1)⋮Cov(Xd,X1)Cov(X1,X2)Var(X2)⋮Cov(Xd,X2)⋯⋯⋱⋯Cov(X1,Xd)Cov(X2,Xd)⋮Var(Xd)
V a r ( x 1 ) Var(x_1) Var(x1)是方差; C o v ( x 1 , x 2 ) Cov(x_1,x_2) Cov(x1,x2)是协方差。
Correlation相关性
协方差 (Covariance):
c o v X Y = σ X Y = E [ ( X − μ X ) ( Y − μ Y ) ] cov_{XY} = \sigma_{XY} = E \big[ (X - \mu_X)(Y - \mu_Y) \big] covXY=σXY=E[(X−μX)(Y−μY)]
相关系数 (Correlation):
c o r r X Y = ρ X Y = E [ ( X − μ X ) ( Y − μ Y ) ] σ X σ Y corr_{XY} = \rho_{XY} = \frac{E \big[ (X - \mu_X)(Y - \mu_Y) \big]}{\sigma_X \sigma_Y} corrXY=ρXY=σXσYE[(X−μX)(Y−μY)]
其中:
- μ X , μ Y \mu_X, \mu_Y μX,μY 分别是 X , Y X, Y X,Y 的均值
- σ X , σ Y \sigma_X, \sigma_Y σX,σY 分别是 X , Y X, Y X,Y 的标准差 (方差的开方)
- ρ X Y \rho_{XY} ρXY 是 X , Y X, Y X,Y 的相关系数,取值范围 [ − 1 , 1 ] [-1, 1] [−1,1]
与协方差的关系------标准化
实例
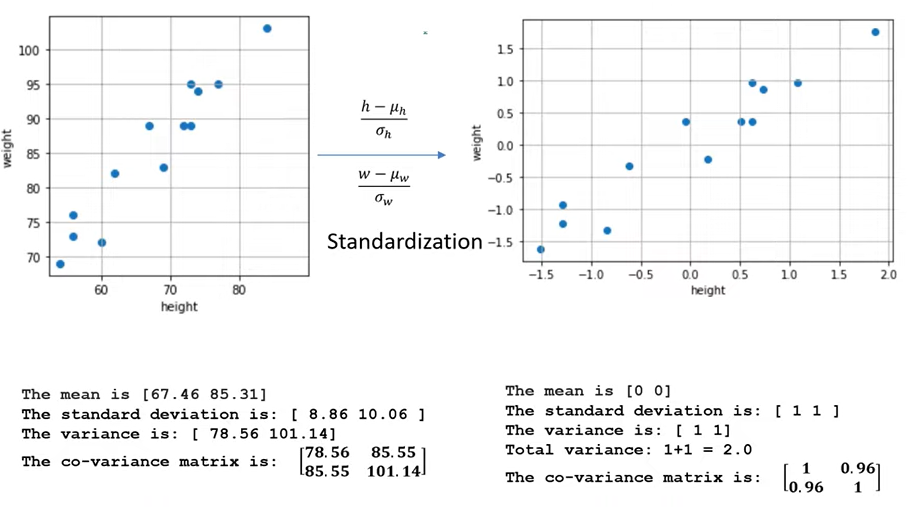
相关系数 = 标准化后变量的协方差
图里的 Standardization(标准化) 指的就是 Z-score 标准化 :
z = x − μ σ z = \frac{x - \mu}{\sigma} z=σx−μ
其中:
- x x x :原始数据
- μ \mu μ :均值 (mean)
- σ \sigma σ :标准差 (standard deviation)