C数据结构：二叉树（下）

1.二叉树递归结构遍历

2.例题

3.二叉树的性质

1.二叉树递归结构遍历

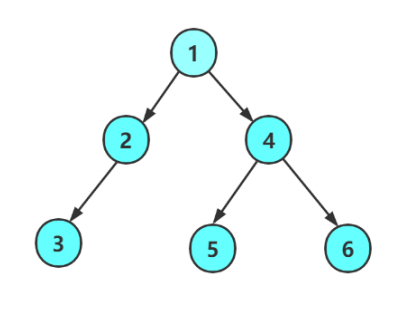
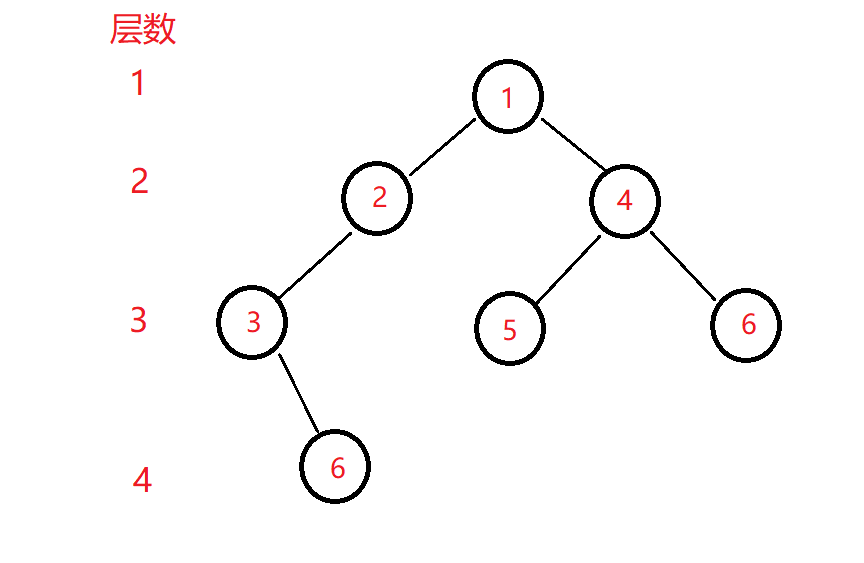
我们先创建一个如下图所示的二叉树。

c 复制代码

typedef int BTDataType;
typedef struct BinaryTreeNode
{
	BTDataType data;
	struct BinaryTreeNode* left;
	struct BinaryTreeNode* right;
}BTNode;
BTNode* BuyNode(int x)//创建节点
{
	BTNode* node = (BTNode*)malloc(sizeof(BTNode));
	if (node == NULL)
	{
		perror("malloc fail");
		return NULL;
	}
	node->data = x;
	node->left = NULL;
	node->right = NULL;
	return node;
}
BTNode* CreatBinaryTree()//创建二叉树
{
	BTNode* node1 = BuyNode(1);
	BTNode* node2 = BuyNode(2);
	BTNode* node3 = BuyNode(3);
	BTNode* node4 = BuyNode(4);
	BTNode* node5 = BuyNode(5);
	BTNode* node6 = BuyNode(6);
	node1->left = node2;
	node1->right = node4;
	node4->left = node5;
	node4->right = node6;
	node2->left = node3;
	return node1;
}

前序遍历

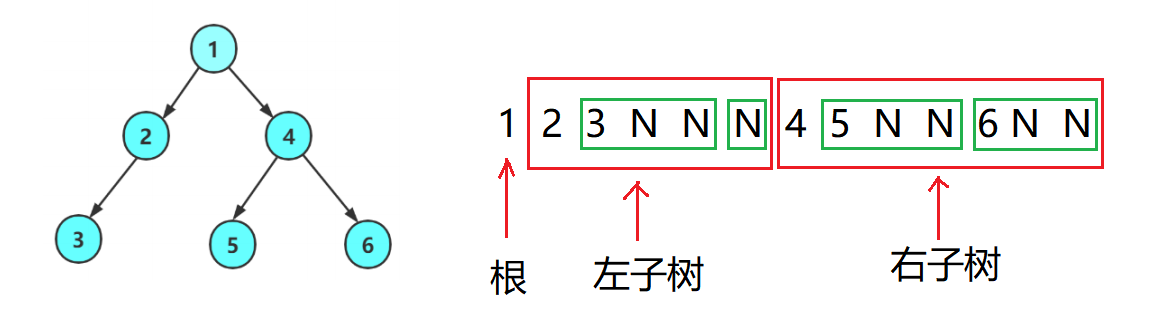
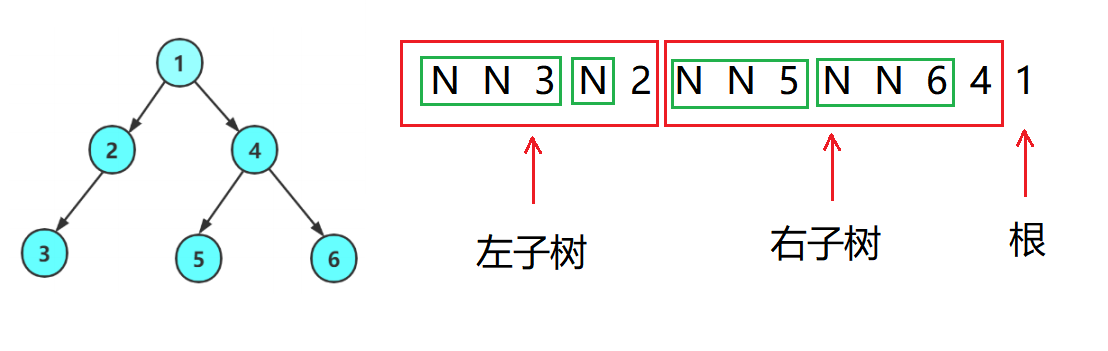
前序遍历即是按照 根、左子树、右子树 的顺序，通过递归结构来遍历。用N代表空树，根据下图可得到前序遍历的序列：1 2 3 N N N 4 5 N N 6 N N

前序代码实现：

c 复制代码

void PrevOrder(BTNode* root)//前序
{
	if (root == NULL)
	{
		printf("N ");
		return;
	}
	else
		printf("%d ", root->data);
	PrevOrder(root->left);
	PrevOrder(root->right);
}

中序遍历

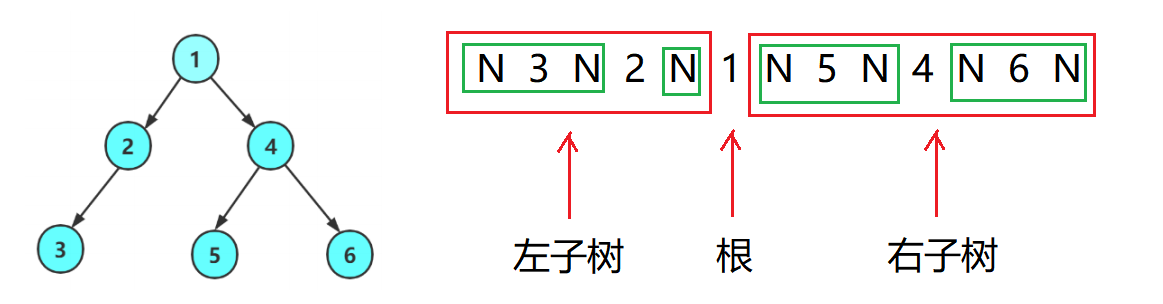
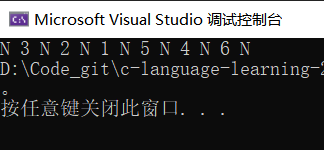
中序遍历即是按照 左子树、根、右子树 的顺序遍历。遍历序列：N 3 N 2 N 1 N 5 N 4 N 6 N 。

中序代码实现：

c 复制代码

void InOrder(BTNode* root)//中序
{
	if (root == NULL)
	{
		printf("N ");
		return;
	}
	else
	{
		InOrder(root->left);
		printf("%d ", root->data);
		InOrder(root->right);
	}
}

后序遍历

后序遍历即是按照 左子树、右子树、根 的顺序遍历。遍历序列：N N 3 N 2 N N 5 N N 6 4 1 。

后序代码实现：

c 复制代码

void BackOrder(BTNode* root)//后序
{
	if (root == NULL)
	{
		printf("N ");
		return;
	}
	else
	{
		BackOrder(root->left);
		BackOrder(root->right);
		printf("%d ", root->data);
	}
}

二叉树的销毁

销毁二叉树应选择后序，若选择前序，销毁根后就找不到左右子树；选择中序，销毁根后就找不到右子树，前序、中序都会导致内存泄漏。所以应先销毁左右子树，再销毁根。

c 复制代码

void TreeDestroy(BTNode* root)//销毁
{
	if (root == NULL)
	{
		return;
	}
	TreeDestroy(root->left);
	TreeDestroy(root->right);
	free(root);
}

2.例题

解决二叉树的相关题目，关键是学会拆分成左右子树 和递归来解决。

求二叉树节点个数

二叉树的节点是由左子树的节点、右子树的节点和根节点组成，写一个求二叉树节点个数的函数，用这个函数求左右子树的节点个数，再加上根节点，即求得整个二叉树的节点个数。

c 复制代码

int TreeSize(BTNode* root)//求二叉树节点个数
{
	return root == NULL ? 0 : TreeSize(root->left) + TreeSize(root->right) + 1;
}

还以是下面的二叉树为例：

求叶数

二叉树的叶节点可以看作叶节点左右子树为空树，所以一个节点左右子树为空树，这个节点就是叶节点。

c 复制代码

int TreeLeafSize(BTNode* root)//求叶数
{
	if (root == NULL)//空树
		return 0;
	if (root->left == NULL && root->right == NULL)//叶节点
		return 1;
	return TreeLeafSize(root->left) + TreeLeafSize(root->right);
}

求树的高度

二叉树的高度为最大层数，可以把二叉树拆分成左右子树，再分别求左右子树的高度，比较后得到高度最大的，再加上根节点，就求出了二叉树的高度。

c 复制代码

int TreeHeight(BTNode* root)//树的高度
{
	if (root == NULL)
		return 0;
	BTDataType leftHeight = TreeHeight(root->left);
	BTDataType rightHeight = TreeHeight(root->right);
	return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;
}

二叉树第k层的节点个数

例如下图的一颗二叉树，若求第3层的节点数，即k=3，可以发现，对于第一层，k=3；对于第二层，k=2；对于第三层，k=1。所以，同样拆分成左右子树，每次递归时通过k-1调整k，当k=1时就返回1，最后再把左右子树求得的第k层的节点数加起来。

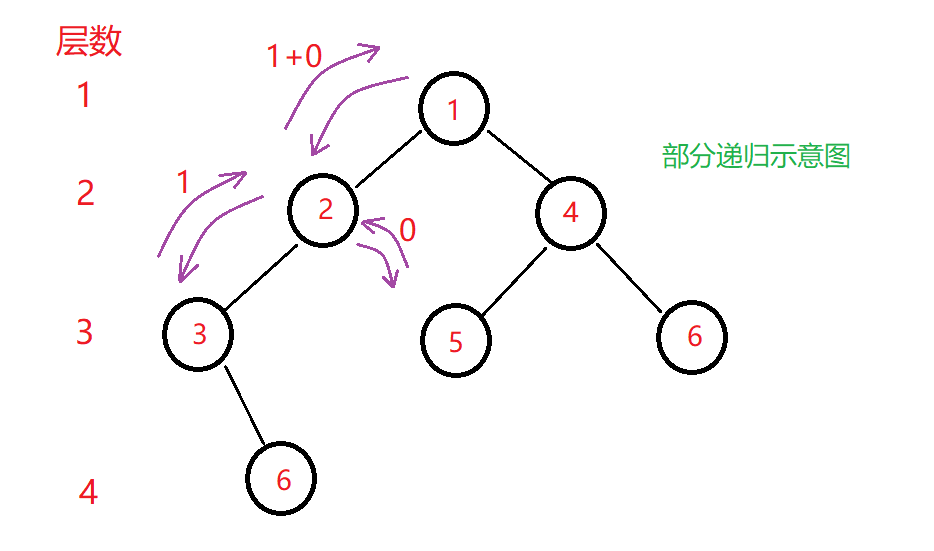
c 复制代码

int TreeLevelKSize(BTNode* root, int k)//二叉树第k层节点个数
{
	if (root == NULL)
	{
		return 0;
	}
	if (k == 1)
	{
		return 1;
	}
	return TreeLevelKSize(root->left, k - 1) + TreeLevelKSize(root->right, k - 1);
}

查找值为x的节点

解决这个问题同样要拆分左右子树和递归，一颗二叉树可能有多个值为x的节点，但函数的返回值只能有一个，当递归遍历找到值为x的节点时，就返回该节点。

c 复制代码

BTNode* TreeFindX(BTNode* root, BTDataType x)//查找值为为x的节点
{
	if (root == NULL)
	{
		return NULL;
	}
	if (root->data == x)
	{
		return root;
	}
	BTNode* ret1=TreeFindX(root->left, x);
	if (ret1)
		return ret1;
	BTNode* ret2 = TreeFindX(root->right, x);
	if (ret2)
		return ret2;
	return NULL;
}

前序遍历二叉树并返回数组

前序遍历一颗二叉树，将二叉树的数据放到数组中并返回数组。

返回数组就需要返回指向数组的指针和数组长度，而数组长度就为二叉树的节点个数。

c 复制代码

int TreeSize(BTNode* root)//求二叉树节点个数
{
	return root == NULL ? 0 : TreeSize(root->left) + TreeSize(root->right) + 1;
}
void preOrder(BTNode* root,int* a,int* pi)//前序遍历二叉树并把数据放入数组
{
    if(root==NULL)
        return;
    a[(*pi)++]=root->data;
    preOrder(root->left,a,pi);
    preOrder(root->right,a,pi);
}
int* preOrderTraversal(BTNode* root,int* returnSize)
{
    *returnSize=TreeSize(root);//数组长度
    int* a(int*)malloc((*returnSize)*sizeof(int));//开辟数组
    int i=0;
    preOrder(root,a,&i);
    return a;
}

访问数组需要知道数组长度，C语言不支持函数返回数组，我们期望经过函数处理数组后得到对应的数组长度，所以我们在主函数定义returnSize=0，将returnSize的地址传入函数，因为如果要通过函数改变主函数中变量的值，就要传址调用，这样就得到了数组长度。

根据前序遍历构建二叉树并输出中序遍历

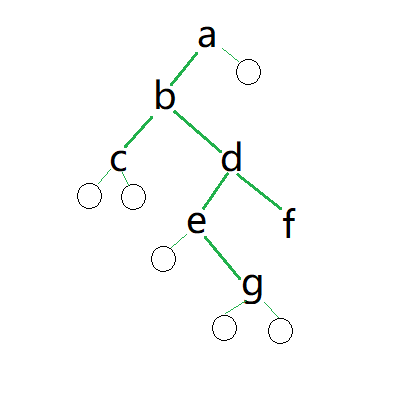
输入前序遍历的字符串，以此建立一个二叉树，再输出中序遍历结果。#表示空树。

这道题的关键是根据前序遍历构建二叉树，所以要前序遍历函数来写创建二叉树的函数。

c 复制代码

BTNode* CreateTree(char* str,int* pi)
{
   if(str[(*pi)]=='#')
   {
      (*pi)++;
      return NULL;
   }
   BTNode* root=(BTNode*)malloc(sizeof(BTNode));
   root->data=str[(*pi)++];
   root->left=CreateTree(str,pi);
   root->right=CreateTree(str,pi);
   return root;
}
void InOrder(BTNode* root)
{
   if(root==NULL)
   {
      printf("#");
      return;
   }
   InOrder(root->left);
   printf("%c",root->data);
   InOrder(root->right);
}
int main()
{
   char str[100];
   scanf("%s",str);
   printf("\n");
   int i=0;
   BTNode* root=CreateTree(str,&i);
   InOrder(root);
   printf("\n");
   return 0;
}

例如，输入前序序列abc##de#g##f###

3.二叉树的性质

非空二叉树的第 i 层最多有2^(i-1)个节点。
高度为h的二叉树的最大节点数为2^(h) - 1。
对任意二叉树，度为0的叶有n0个，度为2的节点有n2个，满足n0 = n2 + 1 。

若一颗完全二叉树有767个节点，则叶的个数是多少？

我们设度为0的节点有N0个，度为1的节点有N1个，度为2的节点有N2个，则N0+N1+N2=767，又在完全二叉树中，度为1的节点数要么为0，要么为1，因为N0 = N2 + 1，所以2N0 + N1 - 1 = 767 ，767为奇数，所以2N0 + N1 - 1也应为奇数，2N0显然为偶数，所以N1应为0，这样等式左边才为奇数，所以最终N0为384，即叶数为384。

拙作一篇，望诸位同道不吝斧正。