图形编辑器开发：基于矩阵的画布缩放和移动实现

大家好，我是前端西瓜哥。

最近在给我的开源图形编辑器 suika 做多 page 功能，需要记录每个 page 的视口信息，在切换 page 的时候进行复原。

suika 图形编辑器 github 地址：

github.com/F-star/suik...

线上体验：

blog.fstars.wang/app/suika/

发现原来的视口管理功能写的不好，于是顺便给它重构掉了。

之前用的是几何算法方案，不好理解和扩展，所以这次改成矩阵来实现了。

所以今天我们来说一说 如何基于矩阵来实现图形编辑器画布缩放功能。

坐标系

二维图形编辑器首先有个场景坐标系，表示图形在真实场景中物体的位置和大小。我们会看到各种写法，如 scene、或是 world、global，它们指的一样东西，表示真实世界。

但我们不可能真的把真实的位置大小绘制到屏幕上，因为屏幕的大小是有限的。为此我们引入了视口（viewport）的概念，即一个观察的窗口，去观测这个场景，需要支持移动这个窗口，缩放窗口里的画面。

你可以将场景理解为房间的一面墙上的壁画，然后有可以到处移动的摄像机（camera），它始终对着这幅壁画，会将真实世界的物体投影到摄像机的屏幕上，在这块屏幕上的画面 对真实世界做了缩放以及裁切。

将场景坐标系的物体转换为视口坐标系的值，是一种线性运算，所以我们通常会引入一个矩阵（viewMatrix）来简洁地表示要进行怎样的变换。

本文会 假设读者对矩阵有基本的了解，不会讲解矩阵内部的运算逻辑，我们只会讲矩阵在视口上的运用，它是怎么去实现基于某个点缩放画布，移动画布，如何让画布自适应某个区域等功能。

ViewportManager 类

业务上会设计一个 ViewportManager 视口类。

或者可以叫做 Camera 摄像机类。但 Camera 这个名字可能更适合 3D 的编辑器，这里还是用 Viewport。

Viewport 类下维护一个名为 viewMatrix 的矩阵对象，并提供视口移动、缩放画布等方法，去对 viewMatrix 进行增量的矩阵运算。

viewMatrix 用于 2D 的图形变换，是个 3x3 的矩阵。

kotlin 复制代码

class ViewportManager {
  private viewMatrix: Matrix;

  constructor() {
    this.viewMatrix = new Matrix();
  }
}

矩阵运算库

我们需要一个矩阵运算库。

虽然很多图形库里面自带矩阵的方法，但我不建议直接使用。

因为它是适配这个图形库的，可能对你的项目地业务并不合适。比如矩阵可能是对象或是类型数组，返回的点可能是它内置的一个类实例，以及会让业务和图形库不够解耦。

流行的有 gl-matrix 库，功能比较丰富。它支持各种维度的矩阵、矢量、以及四元数的运算。不过这个库更合适 3D 编辑器，维护的是可直接用于 webgl 的类型数组，不太合适我的场景。

在 2D 的场景中，我们只需要 3x3 矩阵，所以我下面我会使用 pixijs 提供的 Matrix 类。当然为了通用性，我复制然后改造了一下，使其符合我的业务需求。

用法说明可以看 pixijs 的 matrix 类的文档。

pixijs.download/release/doc...

改造后的代码实现见链接：

codesandbox.io/p/sandbox/6...

Matrix 创建的矩阵的表达为：

css 复制代码

| a | c | tx|
| b | d | ty|
| 0 | 0 | 1 |

渲染

渲染的话，我们需要 将这个 viewView 设置到图形树的根节点的 tranform 上，其下的图形的自身的矩阵会左乘这个矩阵，执行视口的变换运算。

SVG 大概是这样，这里是给根节点的 g 元素设置好 transform。

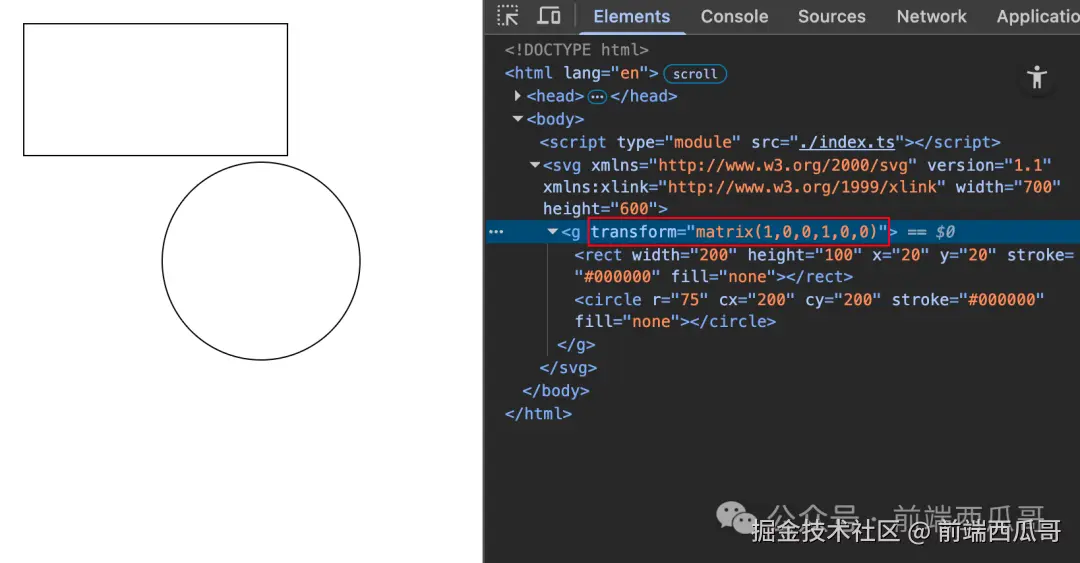
canvas 2d 大概是这样，在最开头的地方调用 ctx.setTransform 方法。

ini 复制代码

const canvas = document.querySelector('canvas');
const ctx = canvas.getContext('2d');

// 初始时设置好 viewMatrix
ctx.setTransform(
  viewMatrix.a,
  viewMatrix.b,
  viewMatrix.c,
  viewMatrix.d,
  viewMatrix.tx,
  viewMatrix.ty,
);

// ...绘制图形。
// 图形也有自己的矩阵，会在原来 viewMatrix 矩阵上右乘新的图形矩阵
// 图形绘制完记得复原矩阵，然后用相同的方式绘制下一个图形。
ctx.save();
ctx.transform(...rect.tranform);
// ...
ctx.restore();

初始化原点居中

图形编辑器初始化时，如果没有内容，将场景坐标系的原点，对齐到视口的中心。

我们拿到 Canvas DOM 元素的宽高，计算出中心点 center。然后创建一个矩阵，修改其位移值为 center，将其设置为 viewMatrix。然后同步修改根结点的 transform，触发重渲染。

矩阵：

复制代码

1 0 cx
0 1 cy
0 0 1

代码：

arduino 复制代码

class ViewportManager {
  // ...

  // 移动到画布中心位置，传入画布宽高
  toCanvasCenter(width, height) {
    const center = {
      x: width / 2,
      y: height / 2,
    }
    this.viewMatrix = new Matrix().translate(center.x, center.y);
  }
}

怎么理解？

理解就是，原来 viewMatrix 初始值是单位矩阵，此时场景坐标系的 (0, 0)，应用 viewMatrix 的矩阵变换为视口坐标，还是 (0, 0)。

但现在我们希望 (0, 0) 变成 (canvasCx, canvasCy)。它们的线性关系很简单，x 和 y 分别加上画布中心点的 x、y。

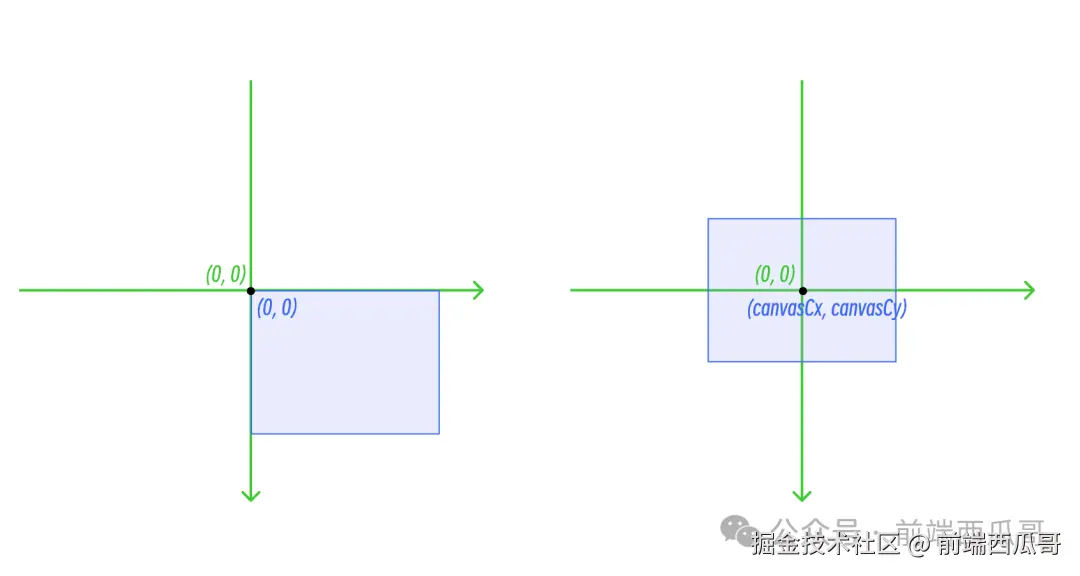
坐标系转换

viewMatrix 的表达其实很简单，就是 缩放和移动，不会有旋转和斜切。

当然有某个特殊的场景可能真会有旋转，那就是可以设置用户坐标系的情况，但属于另一个话题了，不在讨论范围。

矩阵的形式是这样的：

复制代码

scale   0       tx
0       scale   ty
0       0       1

其中 scale 就是画布的缩放比。

不过在视口场景中，我们通常会叫 zoom。所谓 zoom 就是将照相机推进或拉镜头后，实现放大缩小画面的效果。

另外，tx 和 ty 单独来说没什么意义，它们并不代表视口左上角的场景坐标位置，该值为给 (0, 0) 应用 viewMatrix 逆矩阵。

场景坐标系转为视口坐标，对场景位置应用 viewMatrix 矩阵，就能得到视口矩阵的位置。

arduino 复制代码

viewMatrix.apply(scenePt);

视口坐标系转为场景坐标 ，对视口位置应用 viewMatrix 逆矩阵。所谓逆矩阵，就是矩阵运算的反向操作，是可以求出来的。

ini 复制代码

viewMatrix.applyInverse(viewPt);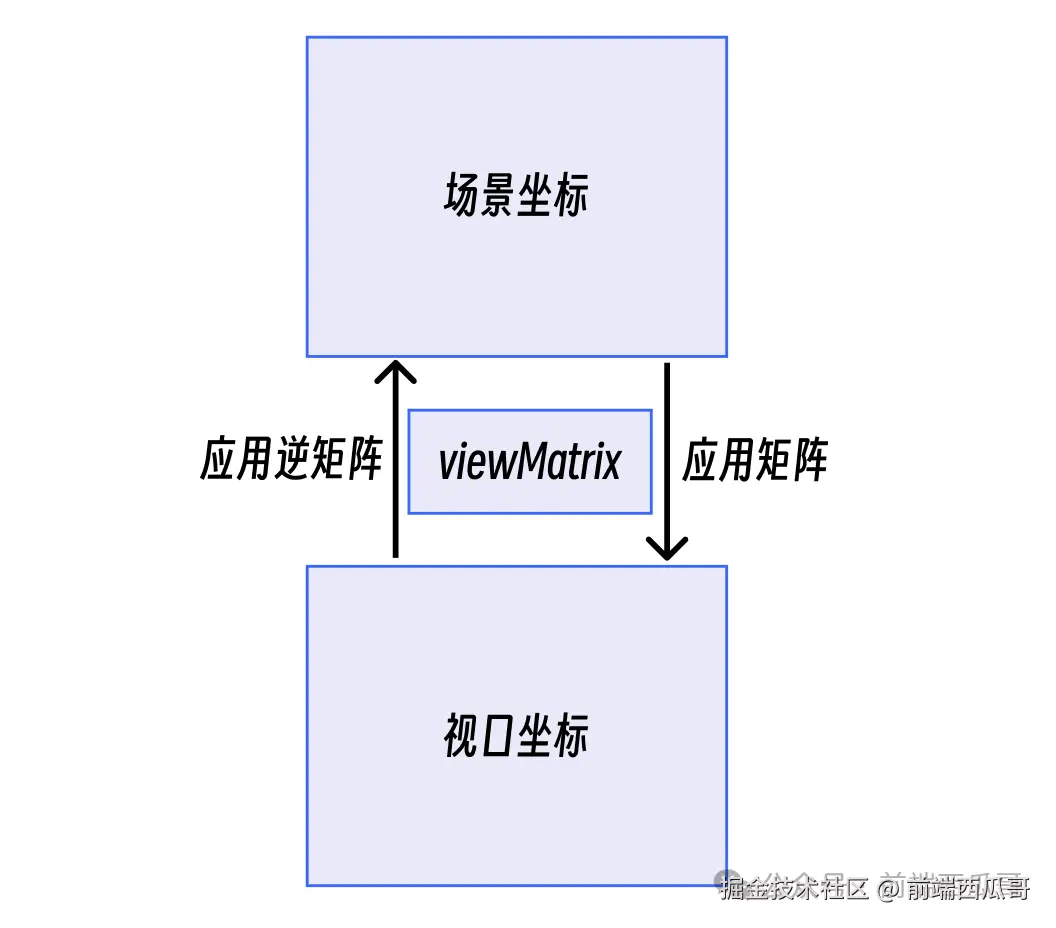

另外还有计算矢量的坐标系转换，矢量比较特殊，相比点，是没有偏移信息的，乘以的是 tx 和 ty 设置为 0 的 viewMatrix，或者你可以理解为只要乘以 zoom 就好了，不需要偏移。

我们给 ViewportManager 加上这些方法。

typescript 复制代码

class ViewportManager {
// ...

// 拿到视口缩放值
  getZoom() {
    returnthis.viewMatrix.a;
  }

// 坐标转换
  toScenePt(x, y) {
    returnthis.viewMatrix.applyInverse({ x, y });
  }
  toViewportPt(x: number, y: number) {
    returnthis.viewMatrix.apply({ x, y });
  }

// 尺寸（矢量）转换
  toSceneSize(size) {
    const zoom = this.getZoom();
    return size / zoom;
  }
  toViewportSize(size) {
    const zoom = this.getZoom();
    return size * zoom;
  }
}

移动画布

移动画布比较简单，在 viewMatrix 再左乘对应的位移矩阵，效果是 tx 和 ty 加上对应的位移值。

注意 dx 和 dy 是 视口坐标系 下的值。

需要左乘的位移矩阵：

复制代码

0   0  dx
0   0  dy
0   0   1

代码：

scss 复制代码

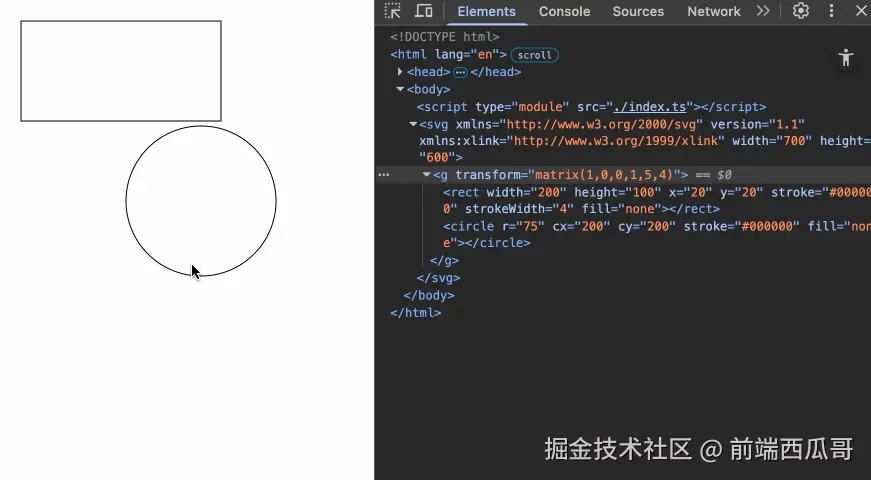
viewMatrix.translate(dx, dy)

通常我们通过鼠标按下，移动的方式来移动画布。

鼠标按下时，记录好此时的 viewMatrix，以及鼠标位置 startCursor。

鼠标移动，计算当前位置和 startCursor 的差值，然后给 viewMatrix 的拷贝左乘这个位移矩阵，然后设置回 viewportManager 对象上。

ini 复制代码

const onMousedown = (e) => {
  startCursor = { x: e.clientX, y: e.clientY };
// 记得 clone
  startMatrix = viewportManager.viewMatrix.clone();
});

const onMousemove = (e) => {
const delta = {
    x: e.clientX - startCursor.x,
    y: e.clientY - startCursor.y,
  };
// 记得 clone
  viewportManager.viewMatrix = startMatrix
    .clone()
    .translate(delta.x, delta.y);

};

缩放画布

以画布上某个点为中心进行缩或放大。

矩阵上的运算，先将场景移动到画布的左上角，然后乘以新 zoom 和原 zoom 的比值，然后场景再移动回来。

需要左乘的矩阵是一个复合矩阵，由三个矩阵相乘得到：

复制代码

0   0  cx  |   dZoom  0      0  |  0   0  -cx
0   0  cy  |   0      dZoom  0  |  0   0  -cy
0   0   1  |   0      0      1  |  0   0   1

代码：

kotlin 复制代码

class ViewportManager {
  // ...

  // 设置新的 zoom 值，此外需要提供缩放中心
  setZoom(zoom, center) {
    const deltaZoom = zoom / this.getZoom();

    this.viewMatrix
      .translate(-center.x, -center.y)
      .scale(deltaZoom, deltaZoom)
      .translate(center.x, center.y);
  }
}

通常我们通过将光标放在画布的某个位置，然后滚动滚轮，然后画布就会基于这个点缩放。

center 就是光标的位置，新的 zoom 会根据滚轮方向按照一定比例算出。

ini 复制代码

const zoomStep = 0.2325;
stage.addEventListener('wheel', (event) => {
let isZoomOut = event.deltaY > 0;
const zoom = viewportManager.getZoom();
let newZoom: number;
if (isZoomOut) {
    newZoom = zoom / (1 + zoomStep);
  } else {
    newZoom = zoom * (1 + zoomStep);
  }
const center = { x: event.clientX, y: event.clientY };

// 更新 viewMatrix
  viewportManager.setZoom(newZoom, center);
});

效果演示：

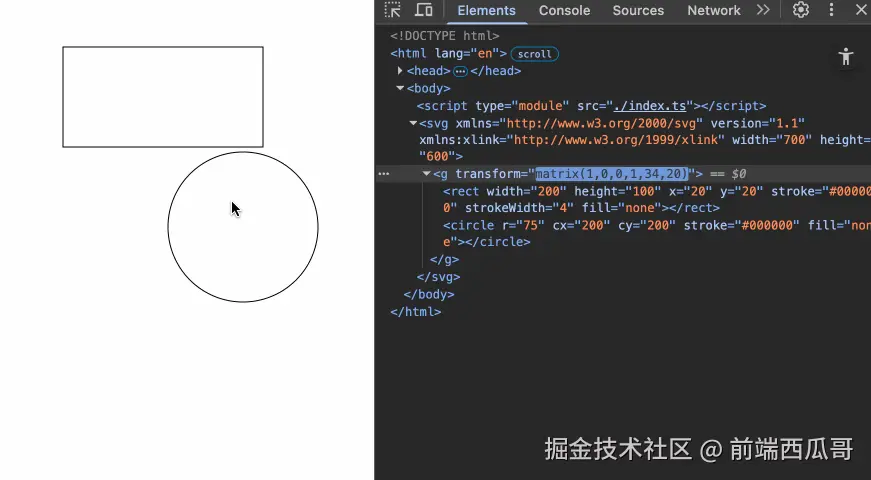
适应到对应区域

还有一个比较常见的需求，就是将画布适应到某个区域（zoomToFit）。

这个区域可能是某个图形的包围盒，比如希望通过双击定位到图形所在位置。可能是多个图形的整体的包围盒，比如画布初始化时，希望可以看到画布上的所有图形，并且在画布中心。

我们实现一个 zoomRectToFit 方法。

arduino 复制代码

const zoomRectToFit = (
  /* 目标区域 */
  targetRect,
  /* 画布宽高 */
  canvasWidth,
  canvasHeight,
  /* 目标区域到画布的 padding */
  padding,
) {
  // 返回一个新的矩阵。
}

首先算好 zoom。

这里要求目标区域使用 "contain" 策略填充画布，所以我们求出图形的 width 和 height 各自需要使用多少比例才能和画布的相等，取其中小的。

ini 复制代码

const zoomX = (canvasWidth - padding * 2) / targetRect.width;
const zoomY = (canvasHeight - padding * 2) / targetRect.height;
let zoom = Math.min(zoomX, zoomY);

完整的流程如下。

计算目标区域的中心位置，让 viewMatrix 先左乘一个 translate(-targetCenter.x, -targetCenter.y) 矩阵，这样目标区域的中心就在视口坐标的原点上；
然后缩放为 zoom，左乘 scale(zoom, zoom)；
最后让这个中心点移动到画布中心，我们需要再左乘 translate(canvasWidth / 2, canvasHeight / 2)。

搞定。

ini 复制代码

const zoomRectToFit = (
  targetRect,
  canvasWidth,
  canvasHeight,
  padding,
) => {
const zoomX = (canvasWidth - padding * 2) / targetRect.width;
const zoomY = (canvasHeight - padding * 2) / targetRect.height;
let zoom = Math.min(zoomX, zoomY);

const targetCenter = {
    x: targetRect.x + targetRect.width / 2,
    y: targetRect.y + targetRect.height / 2,
  };

returnnew Matrix()
    .translate(-targetCenter.x, -targetCenter.y)
    .scale(zoom, zoom)
    .translate(canvasWidth / 2, canvasHeight / 2);
}

对矩形图形进行适应画布的演示：

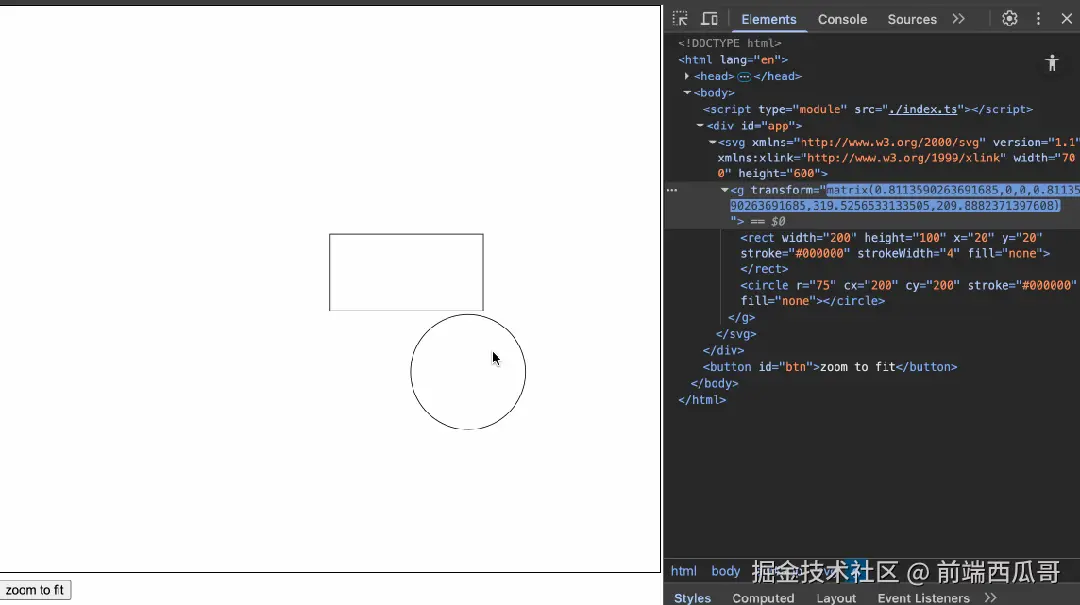
改下矩形的宽高再看看效果：

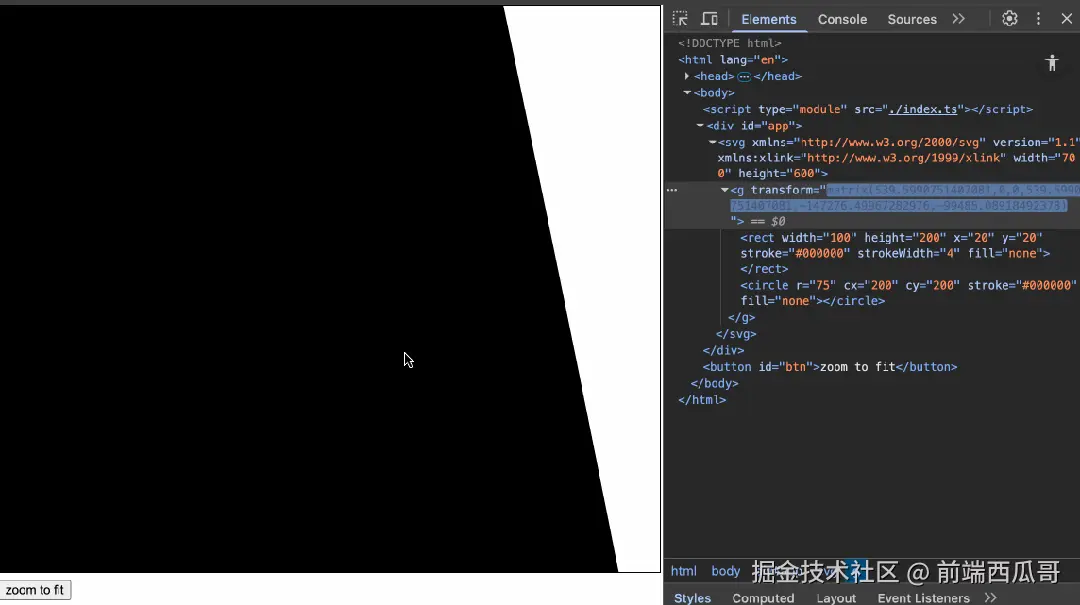
线上 demo

如果你是新手，感觉你可能不太理解，所以我写了一个基于 SVG 的 demo，对着源码阅读文章，能更好理解这里面发生了什么事。

codesandbox.io/p/sandbox/6...

结尾

引入矩阵后，逻辑都变得可以理解了，比之前我也不知道我怎么想出来的几何图形推演好多了。

当然问题变成了你对矩阵是否真的入门了，多看多写应该还是能够大概明白的。

我是前端西瓜哥，关注我，学习更多图形编辑器知识。