【数据结构与算法】（LeetCode）141.环形链表 142.环形链表Ⅱ

文章目录

引言

环形链表问题是数据结构与算法中的经典问题，在面试中出现频率极高。这类问题不仅考察对链表结构的理解，更考验解决问题的思维能力和数学分析能力。本文将详细分析环形链表的判断方法以及环入口节点的定位算法，帮助读者深入理解这一重要问题。

环形链表判断

问题描述

给定一个链表的头节点 head，判断链表中是否存在环。

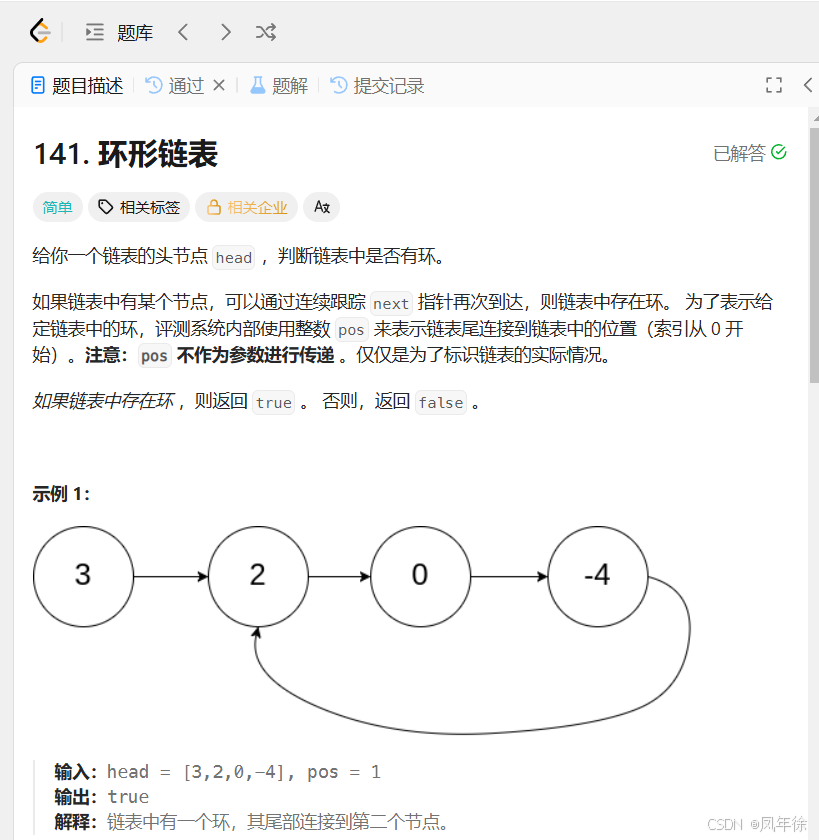
解决方案：快慢指针法

快慢指针法是解决环形链表问题的经典方法，其核心思想是使用两个指针以不同速度遍历链表。

c 复制代码

bool hasCycle(struct ListNode *head) {
    
    struct ListNode* slow=head,*fast=head;
    while(fast&&fast->next)
    {
        slow=slow->next;
        fast=fast->next->next;
        //一定要先让快慢指针走，再判断 因为一开始快慢指针都是head

        if(slow==fast)
        return true;
       
    }
    return false;
    
}

原理分析

为什么快慢指针一定能相遇？

假设慢指针进入环时，快指针与慢指针之间的距离为N。由于快指针每次比慢指针多走一步，它们之间的距离会逐次减少：N, N-1, N-2, ..., 2, 1, 0。因此最终一定会相遇。

步长选择的数学分析

为什么选择一步和两步？

当快指针每次走三步、四步或更多时，情况会变得更加复杂。以三步为例：

每次移动后，快慢指针之间的距离减少2
当N为偶数时，可以追上
当N为奇数时，会错过，距离变为C-1（C为环长）

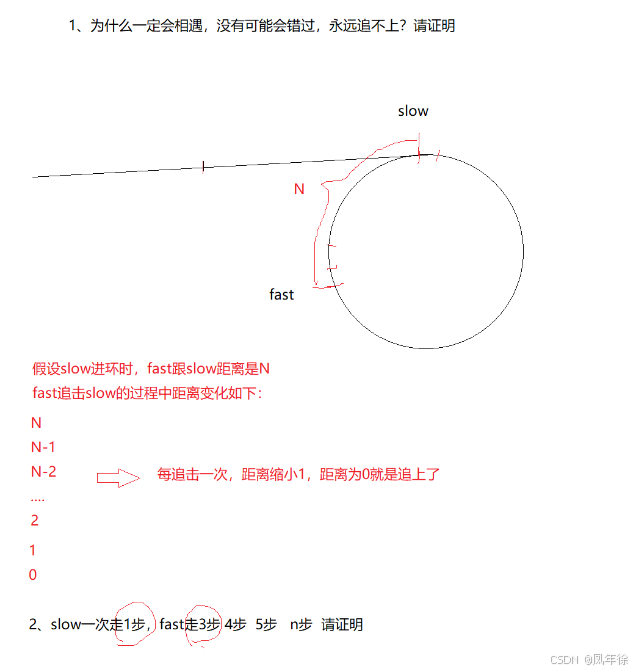
假设slow进环时，fast跟slow的距离是N

fast追击slow时距离变化为N N-1 N-2 ......2 1 0

所以能追上

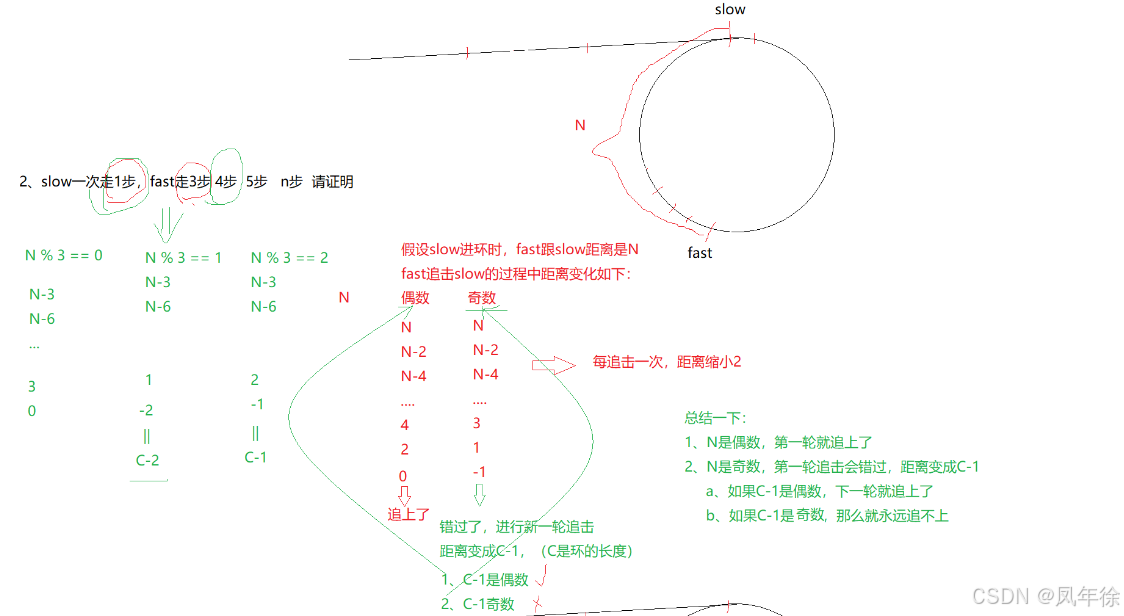
当fast等于3时，每次fast与slow距离就减2

1.当N为偶数时，可以追上

2.当N为奇数时，会错过，这时他们的距离会变为C-1 (假设C为环的长度)

a.如果C-1为偶数(C为奇数)，下一轮就追上了

b.如果C-1为奇数(C为偶数)，就永远追不上

所以这么一看，追不上的条件是:N为奇数并且C为偶数

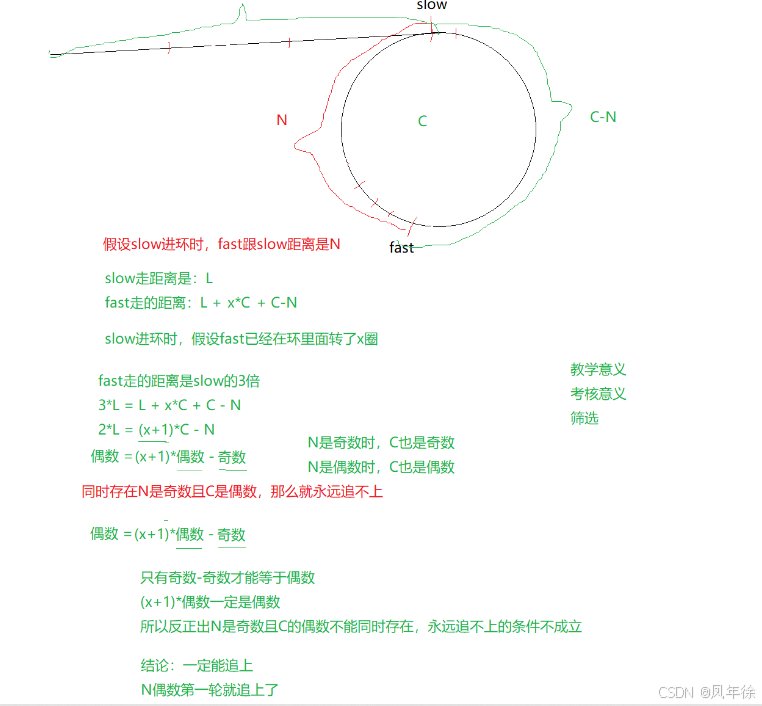
但是这种情况存在吗？

进一步分析表明，当快指针走三步时，追不上的条件是：N为奇数且C为偶数。但通过数学推导可以证明这种情况实际上不可能发生：

假设slow走的距离是L

fast走的距离就是L+x*C+N (x为fast走的圈数)

fast走的距离是slow的3倍

3L=L+x*C+N

化简可得

2L=x*C+N

当C为偶数N为奇数时，x*C为偶数

等号左边是偶数，右边是偶数加奇数（也就是奇数），显然不成立

所以不存在N为奇数，C为偶数的情况

所以fast一定能追上slow

环形链表Ⅱ

题目如下

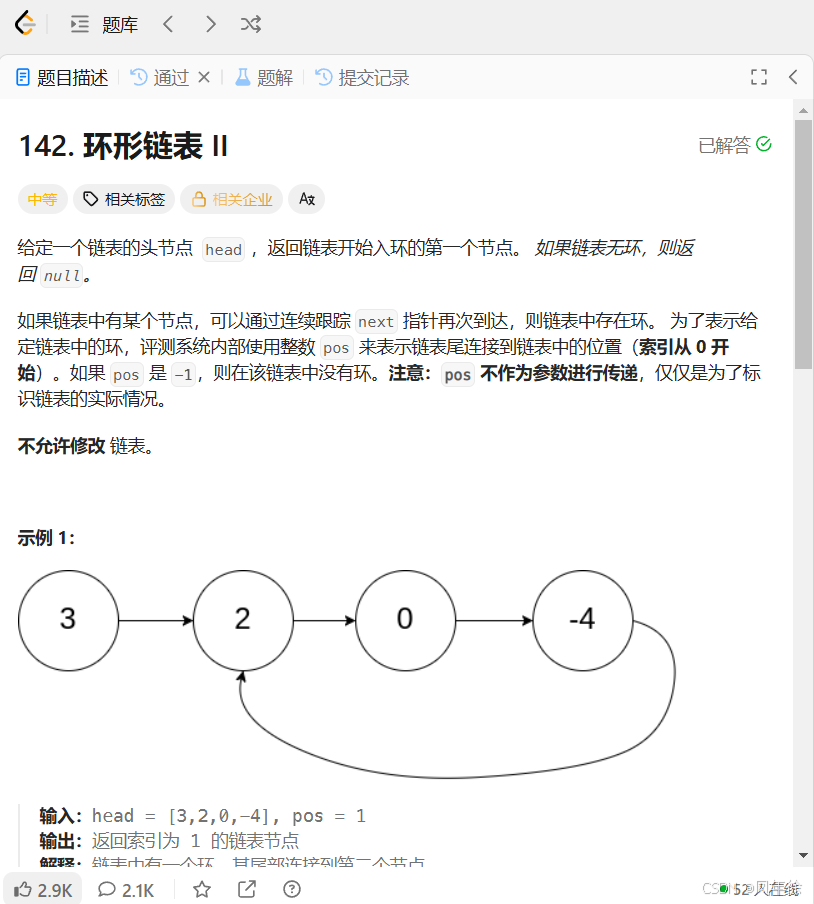
方法一

找到fast与slow相遇的位置meet，head与meet同时走，他们相遇位置就是环的入口

证明如下：

相遇时:

slow走的路程为：L+N

fast走的路程为: L+x*C+N

fast走的是slow的2倍

2(L+N)=L+x*C+N

化简可得

L=(x-1)*C+C-N

所以L的长度就是相遇点转了x-1圈再走了C-N距离的点

这意味着：从头节点到环入口的距离L，等于从相遇点走(x-1)圈再加(C-N)步。因此，两个指针分别从头节点和相遇点出发，一定会在环入口相遇。

代码如下

c 复制代码

struct ListNode *detectCycle(struct ListNode *head) {
    struct ListNode* slow=head,*fast=head;

    while(fast&&fast->next)
    {
        slow=slow->next;
        fast=fast->next->next;

        if(slow==fast)
        {
            struct ListNode * meet=slow;
            while(meet!=head)
            {
                head=head->next;
                meet=meet->next;
                
            }
            return meet;
        }
    }
    return NULL;
}

方法二：转换为相交链表问题

算法思路

找到快慢指针的相遇点
将环从相遇点处断开
问题转换为求两个链表的交点问题

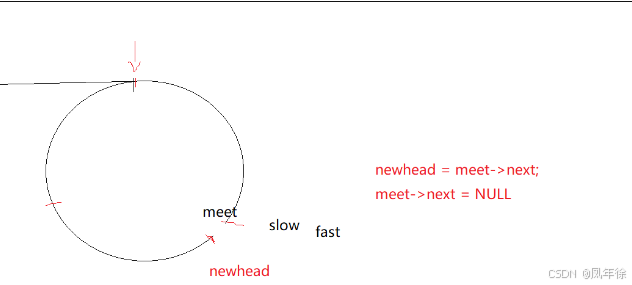
将环形链表断开

newhead=meet->next

meet->next=NULL

这样就转换成了链表相交的问题

c 复制代码

struct ListNode *getIntersectionNode(struct ListNode *headA, struct ListNode *headB) {
    struct ListNode* curA=headA,*curB=headB;
    int lenA=1,lenB=1;
    while(curA->next)
    {
        curA=curA->next;
        lenA++;
    }

    while(curB->next)
    {
        curB=curB->next;
        lenB++;
    }

   

    int gap=abs(lenA-lenB);

    //假设法 先假设A长
    struct ListNode* longList=headA;
    struct ListNode* shortList=headB;
    if(lenA<lenB)
    {
        longList=headB;
        shortList=headA;
    }

    while(gap--)
    {
        longList=longList->next;
    }

    while(longList)
    {
        if(longList==shortList)
        return longList;
        longList=longList->next;
        shortList=shortList->next;
    }
    return NULL;
}

struct ListNode *detectCycle(struct ListNode *head) {
    struct ListNode* slow=head,*fast=head;
    
    while(fast&&fast->next)
    {
        slow=slow->next;
        fast=fast->next->next;
        if(slow==fast)
        {
            struct ListNode* meet=slow;
            struct ListNode* newhead=meet->next;
            meet->next=NULL;
            return getIntersectionNode(head,newhead);
        }
       
    }
   
 return NULL;
    
}

实际应用与扩展

应用场景

内存管理：检测内存泄漏或循环引用
状态机检测：验证有限状态机是否会进入循环状态
递归检测 ：判断递归函数是否会无限递归

meet->next=NULL;

return getIntersectionNode(head,newhead);

}

}

return NULL;

}

复制代码

## 实际应用与扩展

### 应用场景

1. **内存管理**：检测内存泄漏或循环引用
2. **状态机检测**：验证有限状态机是否会进入循环状态
3. **递归检测**：判断递归函数是否会无限递归
4. **哈希冲突解决**：在开放定址法中检测哈希表是否已满