7.22 反向平面分拆和 Hillman--Grassl 对应
定理 7.21.7 的证明涉及形状为 ⟨cr⟩\langle c^r \rangle⟨cr⟩ 的列严格平面分拆与形状包含在 ⟨cr⟩\langle c^r \rangle⟨cr⟩ 中的普通平面分拆之间的双射。很自然地会问,我们是否可以对任意形状 λ\lambdaλ 做类似的双射,从而获得生成函数
∑sh(π)⊆λmax(π)≤tq∣π∣,(7.112)\sum_{\substack{\text{sh}(\pi) \subseteq \lambda \\ \max(\pi) \leq t}} q^{|\pi|}, \tag{7.112}sh(π)⊆λmax(π)≤t∑q∣π∣,(7.112)
的一个公式,其中 π\piπ 遍历所有形状包含在 λ\lambdaλ 中且最大部分 ≤t\leq t≤t 的平面分拆。不幸的是,定理 7.21.7 证明中使用的双射不能推广到非矩形形状。例如,如果 λ=(2,1)\lambda = (2,1)λ=(2,1),那么我们可以将普通平面分拆(允许 0 作为部分)
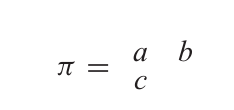
关联到列严格平面分拆(也允许 0 作为部分)
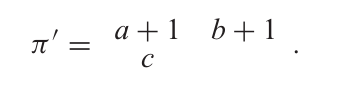
但这样就没有 π\piπ 对应于 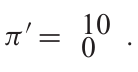
。类似地,如果我们改为尝试
那么就没有 π\piπ 对应于
(因为 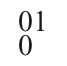
不是一个平面分拆)。实际上,生成函数 (7.112),即使在 t=∞t = \inftyt=∞ 的情况下,一般也不能分解成一个简单的乘积(尽管对于 (7.112) 确实存在一个行列式公式)。
虽然对于给定的形状,在列严格平面分拆和平面分拆之间不存在像用来证明定理 7.21.7 那样的简单对应关系,但在反向情况下确实存在这样的对应关系。这种对应关系对最大部分没有一致的影响,但它在项和方面表现良好。因此我们将得到形状为 λ\lambdaλ 的 nnn 阶反向平面分拆的生成函数。处理形状为 λ\lambdaλ 的弱反向平面分拆 (weak reverse plane partitions) (允许 0 作为部分)更容易。要从形状为 λ\lambdaλ 的弱反向平面分拆 π\piπ 得到一个(非弱)形状为 λ\lambdaλ 的反向平面分拆 π∗\pi^*π∗,只需将 π\piπ 的每个项加 1。注意
∣π∗∣=∣π∣+∣λ∣.|\pi^*| = |\pi| + |\lambda|.∣π∗∣=∣π∣+∣λ∣.
类似地,定义一个弱 SSYT (weak SSYT) 为一个允许 0 作为部分的 SSYT。
7.22.1 定理. 令 λ∈Par\lambda \in \text{Par}λ∈Par。则
∑πq∣π∣=1∏u∈λ[h(u)],(7.113)\sum_{\pi} q^{|\pi|} = \frac{1}{\prod_{u \in \lambda} [h(u)]}, \tag{7.113}π∑q∣π∣=∏u∈λ[h(u)]1,(7.113)
其中 π\piπ 遍历形状为 λ\lambdaλ 的所有弱反向平面分拆。(如果不希望 0 作为部分,只需乘以 q∣λ∣q^{|\lambda|}q∣λ∣。)
证明. 令 T=(aij)T = (a_{ij})T=(aij) 为一个形状为 λ\lambdaλ 的弱 SSYT。通过 πij=aij−i+1\pi_{ij} = a_{ij} - i + 1πij=aij−i+1 定义 π=π(T)\pi = \pi(T)π=π(T)。那么 π\piπ 是一个满足以下条件的形状为 λ\lambdaλ 的弱反向平面分拆:
∣π∣=∣T∣−∑(i−1)λi=∣T∣−b(λ).|\pi| = |T| - \sum(i - 1)\lambda_i = |T| - b(\lambda).∣π∣=∣T∣−∑(i−1)λi=∣T∣−b(λ).
容易看出这个对应是一个双射。因此,如果 Rλ\mathcal{R}\lambdaRλ(分别地,Rλ′\mathcal{R}'\lambdaRλ′) 表示形状为 λ\lambdaλ 的所有弱反向平面分拆(分别地,弱 SSYT)的集合,那么
∑π∈Rλq∣π∣=q−b(λ)∑T∈Rλ′q∣T∣\sum_{\pi \in \mathcal{R}\lambda} q^{|\pi|} = q^{-b(\lambda)} \sum{T \in \mathcal{R}'\lambda} q^{|T|}π∈Rλ∑q∣π∣=q−b(λ)T∈Rλ′∑q∣T∣
=q−b(λ)sλ(1,q,q2,...),= q^{-b(\lambda)} s\lambda(1, q, q^2, \ldots),=q−b(λ)sλ(1,q,q2,...),
证明由推论 7.21.3 得出。 ∎
定理 7.22.1 如此优雅,以至于我们可能会寻求一个简单的双射证明。将 λ\lambdaλ 与其图等同,我们想要在形状为 λ\lambdaλ 的弱反向平面分拆 π\piπ 和函数 f:λ→Nf : \lambda \to \mathbb{N}f:λ→N 之间建立一个双射,使得
∣π∣=∑u∈λf(u)h(u).|\pi| = \sum_{u \in \lambda} f(u) h(u).∣π∣=u∈λ∑f(u)h(u).
我们现在描述这样一个双射,称为 Hillman--Grassl 对应 (Hillman--Grassl correspondence)。
我们将连续定义对 (π0,f0),(π1,f1),...,(πk,fk)(\pi_0, f_0), (\pi_1, f_1), \ldots, (\pi_k, f_k)(π0,f0),(π1,f1),...,(πk,fk),其中每个 πi\pi_iπi 是一个形状为 λ\lambdaλ 的弱反向平面分拆且 fi:λ→Nf_i : \lambda \to \mathbb{N}fi:λ→N。我们从 π0=π\pi_0 = \piπ0=π 和所有 u∈λu \in \lambdau∈λ 的 f0(u)=0f_0(u) = 0f0(u)=0 开始。我们通过将 πi\pi_iπi 的某个方格 ui∈λu_i \in \lambdaui∈λ(待解释)中的项减少 h(ui)h(u_i)h(ui) 个 1 来从 πi\pi_iπi 得到 πi+1\pi_{i+1}πi+1,并且我们定义
fi+1(v)={fi(v),v≠uifi(ui)+1,v=uif_{i+1}(v) = \begin{cases} f_i(v), & v \neq u_i \\ f_i(u_i) + 1, & v = u_i \end{cases}fi+1(v)={fi(v),fi(ui)+1,v=uiv=ui
最终 πk\pi_kπk 的所有项将等于 0。因此,
∣π∣=∑u∈λfk(u)h(u),|\pi| = \sum_{u \in \lambda} f_k(u) h(u),∣π∣=u∈λ∑fk(u)h(u),
并且我们定义 f=fkf = f_kf=fk。
剩下的就是描述从 πi\pi_iπi 得到 πi+1\pi_{i+1}πi+1 的规则,以及相应的 ui∈λu_i \in \lambdaui∈λ 的选择。我们将在 λ\lambdaλ 中定义一条具有步长 NNN 或 EEE(即向上移动一个方格或向右移动一个方格)的格路 LLL,从 λ\lambdaλ 的一列的底部开始并在 λ\lambdaλ 的一行的末端结束。格路 LLL 从 πi\pi_iπi 的最西南非零项的位置开始。如果路径到达方格 (a,b)(a, b)(a,b),那么如果 (πi)ab=(πi)a−1,b>0(\pi_i){ab} = (\pi_i){a-1, b} > 0(πi)ab=(πi)a−1,b>0 则移动 NNN;否则如果 (πi)ab>0(\pi_i){ab} > 0(πi)ab>0 则移动 EEE。当无法再移动时,格路终止。定义πi+1\pi{i+1}πi+1为通过以下方式从 πi\pi_iπi 得到的数组:将路径LLL 所经过的每个方格中的对应项(entry)均减去 1。如果 LLL 起始于列 bbb 并终止于行 aaa,那么令 ui=(a,b)u_i = (a, b)ui=(a,b)。容易看出 #L=h(ui)\#L = h(u_i)#L=h(ui)。
我们用一个形状为 (3,3,1)(3, 3, 1)(3,3,1) 的反向平面分拆 π\piπ 来说明这个对应关系。我们用粗体表示格路 LLL,并通过在方格 u∈λu \in \lambdau∈λ 中放入值 fi(u)f_i(u)fi(u) 来表示函数 fif_ifi。

我们省略了证明该对应确实是一个双射的部分,除了提示方格 uiu_iui 在所有方格 u1,...,uiu_1, \ldots, u_iu1,...,ui 中位于最右边的列,并且在其列中的方格 u1,...,uiu_1, \ldots, u_iu1,...,ui 中位于最高的行。
现在令 PPP 为一个 nnn 元偏序集,并令 A(P)A(P)A(P) 表示第 3.15 节中的 PPP-分拆的集合。由定理 3.15.7 回忆
GP(q):=∑σ∈A(P)q∣σ∣=WP(q)(1−q)⋯(1−qn),G_P(q) := \sum_{\sigma \in A(P)} q^{|\sigma|} = \frac{W_P(q)}{(1 - q) \cdots (1 - q^n)},GP(q):=σ∈A(P)∑q∣σ∣=(1−q)⋯(1−qn)WP(q),
其中 WP(1)=e(P)W_P(1) = e(P)WP(1)=e(P),即 PPP 的线性扩张数。如果我们设 P=Pλ∗P = P_\lambda^*P=Pλ∗,即推论 7.19.5 之后定义的偏序集 PλP_\lambdaPλ 的对偶,那么方程 (7.113) 的左边正好是 GP(q)G_P(q)GP(q)。因此我们得到
fλ=e(Pλ)=e(Pλ∗)=[n]!∏u∈λ[h(u)]∣q=1=n!∏u∈λh(u)∣q=1(7.114)f^\lambda = e(P_\lambda) = e(P_\lambda^*) = \left. \frac{[n]!}{\prod_{u \in \lambda} [h(u)]} \right|{q=1} = \left. \frac{n!}{\prod{u \in \lambda} h(u)} \right|_{q=1} \tag{7.114}fλ=e(Pλ)=e(Pλ∗)=∏u∈λ[h(u)][n]! q=1=∏u∈λh(u)n! q=1(7.114)
给出了钩长公式(推论 7.21.6)的一个避免使用行列式的证明。