数据集在作业一
线性不可分逻辑回归
线性不可分逻辑回归是逻辑回归在线性不可分数据集上的应用形式。当数据集不存在能完全分隔两类样本的线性超平面(即两类样本的分布相互交织,无法用直线 / 平面彻底分开)时,逻辑回归通过概率建模和损失函数优化,仍然可以学习一个最优的线性决策边界,实现对样本类别的概率预测。
核心特点
与线性可分情况的本质区别在于:
-
线性可分:存在完美分隔超平面,模型可实现 100% 分类准确率。
-
线性不可分:不存在完美分隔超平面,无论如何选择参数,总会有样本被误分类,模型需在 "尽可能正确分类多数样本" 和 "控制错误分类的代价" 之间权衡。
数学定义

代码
数据读取及可视化
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from stack_data import markers_from_ranges
"""读取数据集"""
data=pd.read_csv('ex2data2.txt',names=['Exam 1 score','Exam 2 score','Admitted'])
# print(data.head())
"""数据可视化"""
fig,ax=plt.subplots()
ax.scatter(data[data['Admitted'] == 1]['Exam 1 score'], data[data['Admitted'] == 1]['Exam 2 score'], c='b', marker='o', label='Admitted')
ax.scatter(data[data['Admitted']==0]['Exam 1 score'],data[data['Admitted']==0]['Exam 2 score'],c='r',marker='x',label='Not Admitted')
ax.legend()
ax.set_xlabel('Exam 1 score')
ax.set_ylabel('Exam 2 score')
plt.show()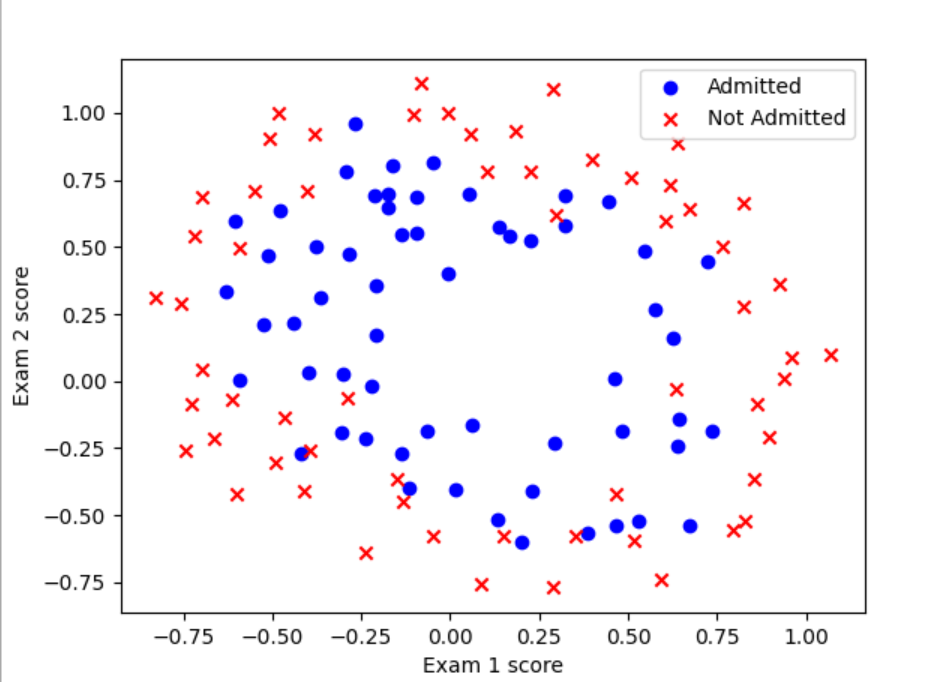
这里我们明显无法通过线性进行分类处理,而如果要做到非线性,就需要用高阶特征,这样可以更好的拟合(可以联系一次函数和高次函数来理解)
特征映射,创建高阶项特征,目的是为了更好地拟合数据,但是会导致过拟合,所以要进行正则化
def feature_mapping(x1,x2,power):
data={}
for i in range(power+1):
for j in range(i+1):
data[f'F{i},{j}']=np.power(x1,i-j)*np.power(x2,j)
return pd.DataFrame(data)预处理数据集
x1=data['Exam 1 score']
x2=data['Exam 2 score']
power=6
data2=feature_mapping(x1,x2,power)
# print(data.head())
"""构建数据集"""
X=data2.values
# print(X.shape)
y=data['Admitted']
# print(y.shape)
y=y.values
# print(y.shape)
y=y.reshape((y.shape[0],1))输出层激活函数
def sigmoid(z):
return 1/(1+np.exp(-z))损失函数(含正则化的交叉熵损失函数)
def cost_function(X,y,theta,lambda_reg):
A=sigmoid(np.dot(X,theta))
first=y*np.log(A)
second=(1-y)*np.log(1-A)
reg=np.sum(np.power(theta[1:],2))*lambda_reg/(2*len(X))
return -np.sum(first+second)/len(X)+reg正则化(Regularization)的核心概念
正则化是机器学习中用于缓解过拟合的关键技术。过拟合指模型在训练数据上表现极好,但在未见过的测试数据上表现很差(过度 "死记硬背" 训练数据中的细节和噪声,而非学习通用规律)。
正则化的核心思想是:在模型的损失函数中加入 "惩罚项"(Penalty Term),通过惩罚 "复杂模型"(通常表现为参数绝对值过大),迫使模型选择更简单、泛化能力更强的参数组合,从而平衡 "拟合训练数据" 和 "保持模型简单" 之间的关系。


初始化参数
theta=np.zeros((X.shape[1],1))
lambda_reg=1
cost=cost_function(X,y,theta,lambda_reg)
alpha=1.9
iters=200000
lamda=0.01正则化梯度
def gradient_reg(theta,X,y,lamda):
reg=theta[1:]*(lamda/len(X))
reg=np.insert(reg,0,0,0)
first=np.dot(X.T,(sigmoid(np.dot(X,theta))-y))/len(X)
return first+reg梯度下降
def gradient_descent(X,y,theta,alpha,count,lambda_reg):
costs=[]
for i in range(count):
theta=theta-alpha*(1/len(X))*gradient_reg(theta,X,y,lambda_reg)
cost=cost_function(X,y,theta,lambda_reg)
costs.append(cost)
if i%1000==0:
print(cost)
return theta,costs
theta_final,costs=gradient_descent(X,y,theta,alpha,iters,lamda)预测
def predict(X,theta):
prob=sigmoid(np.dot(X,theta))
return [1 if x>=0.5 else 0 for x in prob]
y_pred=np.array(predict(X,theta_final))
y_pred=y_pred.reshape((y_pred.shape[0],1))
accuracy=np.mean(y_pred==y)
print(accuracy)#0.847457627118644总结
读取数据集------预处理(创建高阶项)------损失函数(L2正则化)------梯度函数------梯度下降------预测