TensorFlow深度学习实战（35）——概率神经网络

TensorFlow深度学习实战（35）------概率神经网络

- [0. 前言](#0. 前言)
- [1. 贝叶斯网络](#1. 贝叶斯网络)
- [2. 处理预测中的不确定性](#2. 处理预测中的不确定性)
- - [2.1 不确定性](#2.1 不确定性)
  - [2.2 创建合成数据集](#2.2 创建合成数据集)
  - [2.3 构建回归模型](#2.3 构建回归模型)
- [3. 用于偶然不确定性的概率神经网络](#3. 用于偶然不确定性的概率神经网络)
- [4. 认知不确定性](#4. 认知不确定性)
- 小结
- 系列链接

0. 前言

不确定性在物理世界中随处可见，无论是进行分类任务还是回归任务，了解模型对其预测的置信度至关重要。传统深度学习模型虽然在许多任务中表现出色，但它们无法处理不确定性。相反，它们本质上是确定性的。在本节中，我们将学习如何利用TensorFlow Probability构建可以处理不确定性的模型，包括概率深度学习模型和贝叶斯网络。

1. 贝叶斯网络

贝叶斯网络 (Bayesian Network, BN) 利用图论、概率和统计学中的概念封装复杂的因果关系。本节，我们将构建一个有向无环图 (Directed Acyclic Graph, DAG)，其中节点称为因子(随机变量)，通过箭头连接，箭头表示因果关系。每个节点代表一个具有相关概率的变量，也称条件概率表 (Conditional Probability Table, CPT)，连接表示一个节点对另一个节点的依赖关系。贝叶斯网络弥补了标准深度学习模型无法表示因果关系的缺陷。

贝叶斯网络的优势在于能够结合专家知识和数据来建模不确定性。由于能够进行概率和因果推理，贝叶斯网络在各种领域得到了广泛应用。贝叶斯网络的核心是贝叶斯定理：
P ( A ∣ B ) = P ( B ∣ A ) P ( A ) P ( B ) P(A|B)=\frac{P(B|A)P(A)}{P(B)} P(A∣B)=P(B)P(B∣A)P(A)

贝叶斯定理用于确定在特定条件下事件的联合概率。理解贝叶斯网络最简单的方法是，它可以确定假设与证据之间的因果关系。有一个未知的假设 H，我们希望评估其不确定性并做出决策，从对假设 H 的先验开始，然后基于证据 E 更新对 H 的先验。

例如，有一个带有洒水器的草地。根据常识，我们知道如果洒水器打开了，草地会湿。那么，反之，如果发现草地潮湿，那么洒水器开着的概率是多少？草地潮湿是因为下雨的概率又是多少？进一步添加证据，在天空是多云的情况下，草地潮湿是因为下雨的概率将会变为多少？

这种基于证据的推理通过贝叶斯网络以有向无环图的形式表现出来，这种图也被称为因果图 (causal graph)，因为它们提供了因果关系。

为了建模此问题，使用 JointDistributionCoroutine 分布类，从单个模型中同时进行数据采样和联合概率计算。利用以下假设构建模型：

天气多云的概率是 0.2
天气多云且下雨的概率是 0.8，而不是多云但下雨的概率是 0.1
天气多云且洒水器开着的概率是 0.1，而不是多云但洒水器开着的概率是 0.5
对于该问题，有四种可能性：

洒水器	下雨	草地潮湿
F	F	0
F	T	0.8
T	F	0.9
T	T	0.99

相应的贝叶斯网络 DAG 如下。

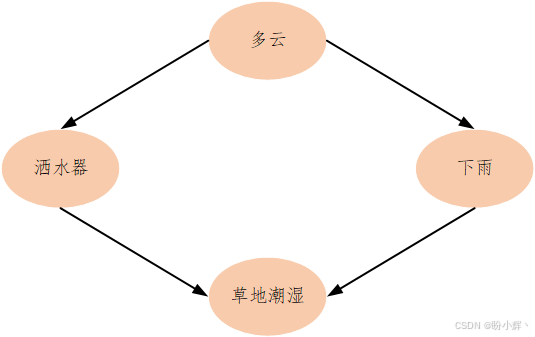
这些信息可以通过以下模型表示：

python 复制代码

import tensorflow as tf
from tensorflow_probability.python import distributions as tfd
import tensorflow_probability.python.experimental.marginalize as marginalize
import functools
import itertools

Root = tfd.JointDistributionCoroutine.Root
def model():
    cloudy = yield Root(tfd.Bernoulli(probs=0.2, dtype=tf.int32))
    sprinkler_prob = [0.5, 0.1]
    sprinkler_prob = tf.gather(sprinkler_prob, cloudy)
    sprinkler = yield tfd.Bernoulli(probs=sprinkler_prob, dtype=tf.int32)
    raining_prob = [0.1, 0.8]
    raining_prob = tf.gather(raining_prob, cloudy)
    raining = yield tfd.Bernoulli(probs=raining_prob, dtype=tf.int32)

    grass_wet_prob = [[0.0, 0.8],
                      [0.9, 0.99]]
    grass_wet_prob = tf.gather_nd(grass_wet_prob, _stack(sprinkler, raining))
    grass_wet = yield tfd.Bernoulli(probs=grass_wet_prob, dtype=tf.int32)

上述模型作为数据生成器。Root 函数用于表示图的根节点，定义函数 broadcast 和 stack。

python 复制代码

def _conform(ts):
    """Broadcast all arguments to a common shape."""
    shape = functools.reduce(
        tf.broadcast_static_shape, [a.shape for a in ts])
    return [tf.broadcast_to(a, shape) for a in ts]

def _stack(*ts):
    return tf.stack(_conform(ts), axis=-1)

为了进行推理，使用 MarginalizableJointDistributionCoroutine 类，因为它可以计算边缘概率：

python 复制代码

d = marginalize.MarginalizableJointDistributionCoroutine(model)

示例 1

观察到草地是湿的(对应的观察值是 1------如果草地是干的，将其设为 0)，我们不知道云的状态或洒水器的状态(未知状态的观察值设置为 marginalize)，我们想知道下雨的概率(想找的概率对应的观察值设置为 tabulate) ，向模型提供观察值 observations：

python 复制代码

# We want to know the probability that it was raining and we want to marginalize over the state of the sprinkler.
observations = ['marginalize',  # We don't know the cloudy state
                'tabulate', # We want to know the probability it rained.
                'marginalize',  # We don't know the sprinkler state.
                1]              # We observed a wet lawn.
p = tf.exp(d.marginalized_log_prob(observations))
p = p / tf.reduce_sum(p)

获取下雨的概率：

python 复制代码

print(p.numpy())

结果为 [0.27761015 0.72238994]，即下雨的概率是 0.722。

示例 2

如果观察到草地是湿的，对云的状态或是否下雨一无所知，想知道洒水器是否开启，向模型提供观察值 observations：

python 复制代码

observations = ['marginalize',  
                'marginalize', 
                'tabulate',  
                1]              
p = tf.exp(d.marginalized_log_prob(observations))
p = p / tf.reduce_sum(p)

得到结果为 [0.61783344, 0.38216656]，即洒水器开启的概率为 0.382。

示例 3

如果观察到没有下雨，并且洒水器关闭了，想知道草地的状态。逻辑上，草地不应该是湿的。我们通过模型进行确认，向模型提供观察值 observations：

python 复制代码

observations = ['marginalize',  
                0, 
                0 ,  
                'tabulate']              
p = tf.exp(d.marginalized_log_prob(observations))
p = p / tf.reduce_sum(p)

得到结果为 [1., 0]，即草地是干的概率为 100%。

一旦我们知道了父节点的状态，就不需要知道父节点的父节点的状态------即贝叶斯网络遵循局部马尔可夫性质。在本节示例中，我们从结构开始，得到条件概率，并演示了如何基于模型进行推理，尽管模型和条件概率分布相同，证据仍然能够改变后验概率。

在贝叶斯网络中，结构(节点及其相互连接的方式)和参数(每个节点的条件概率)是从数据中学习的，分别称为结构学习和参数学习。

2. 处理预测中的不确定性

我们已经讨论了深度学习模型中的预测不确定性，经典的深度学习架构无法考虑这些不确定性。在本节中，我们将使用 TensorFlow Probability (TFP) 提供的网络层来建模不确定性。

2.1 不确定性

在添加 TFP 网络层之前，首先介绍不确定性。不确定性有两个类别：

偶然不确定性 (Aleatory Uncertainty)：偶然不确定性源于自然过程的随机特性，是固有的不确定性，由于概率性而存在。例如，在掷硬币时，总会有一定程度的不确定性在预测下一次掷出的结果是正面还是反面。这种不确定性无法消除，本质上，每次重复实验时，结果都会有一定的变化
认知不确定性 (Epistemic Uncertainty)：认知不确定性来源于知识的缺乏。可能有各种原因导致知识缺乏，例如对底层过程的不充分理解、对现象的不完整了解等等。通过理解原因，例如获取更多数据，可以减少这种不确定性。

不确定性的存在增加了风险，我们需要一种方法来量化不确定性，从而量化风险。

2.2 创建合成数据集

在本节中，我们将学习如何修改标准深度神经网络以量化不确定性。从创建合成数据集开始。为了创建数据集，假设输出预测 y y y 线性依赖于输入 x x x：
y i = 2.7 x i + 3 + 0.74 ϵ y_i=2.7x_i+3+0.74\epsilon yi=2.7xi+3+0.74ϵ

其中， ϵ \epsilon ϵ 服从均值为 0、标准差为 1 的正态分布。

使用 create_dataset 函数生成合成数据。为了生成这些数据，使用了 TFP distributions 中的均匀分布和正态分布：

python 复制代码

import tensorflow_probability as tfp
import matplotlib.pyplot as plt
import numpy as np
import tensorflow as tf
from tensorflow.keras.layers import Dense
from tensorflow.keras import Sequential

tfd = tfp.distributions

def create_dataset(n, x_range):
    x_uniform_dist = tfd.Uniform(low=x_range[0], high=x_range[1])
    x = x_uniform_dist.sample(n).numpy() [:, np.newaxis] 
    y_true = 2.7*x+3
    eps_uniform_dist = tfd.Normal(loc=0, scale=1)
    eps = eps_uniform_dist.sample(n).numpy() [:, np.newaxis] *0.74*x
    y = y_true + eps
    return x, y, y_true

y_true 是不包含正态分布噪声 ϵ \epsilon ϵ 的真实值。

接下来，创建训练数据集和验证数据集：

python 复制代码

x_train, y_train, y_true = create_dataset(2000, [-10, 10])
x_val, y_val, _ = create_dataset(500, [-10, 10])
def plot_dataset(x_train, y_train, x_val, y_val, y_true, title):
    fig = plt.figure(figsize = (10, 10))
    plt.scatter(x_train, y_train, marker='+', label='Training data')
    plt.scatter(x_val, y_val, marker='*', color='r', label='Validation data')
    plt.plot(x_train, y_true, color='b', label='Ground Truth')
    plt.title(title)
    plt.xlabel('$x$')
    plt.ylabel('$y$')
    plt.legend()
    plt.show()

plot_dataset(x_train, y_train, x_val, y_val, y_true, 'Synthetic Dataset')

x_test = np.linspace(-10, 10, 1000).reshape(-1, 1)

得到 2,000 个训练数据样本和 500 个验证数据样本，如下所示，Ground Truth 表示没有任何噪声的真实值 y y y：

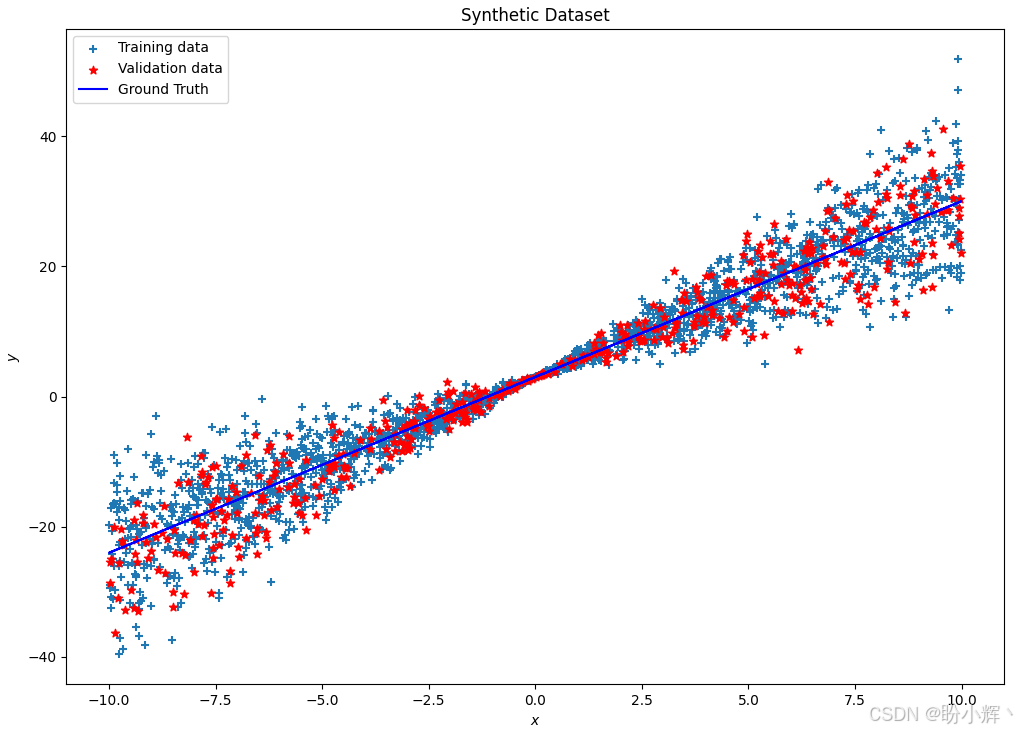
2.3 构建回归模型

可以构建一个简单的 TensorFLow 模型来对创建的合成数据集执行回归任务：

python 复制代码

# Model Architecture
model = Sequential([Dense(1, input_shape=(1,))])

# Compile 
model.compile(loss='mse', optimizer='adam')

# Fit
model.fit(x_train, y_train, epochs=100, verbose=2)

y_pred = model(x_test)

# Plot the data and a trained regression line
plt.figure(figsize=(10, 10))
plt.scatter(x_train, y_train, alpha=.5, label='Training Data')
plt.plot(x_train, y_true, color='k', label='Ground Truth')
plt.plot(x_test, y_pred, label='Fitted line', c='r')
plt.xlabel('$x$')
plt.ylabel('$y$')
plt.title('Regression using Neural Network')
plt.legend()
plt.show()

观察拟合模型在测试数据集上的表现：

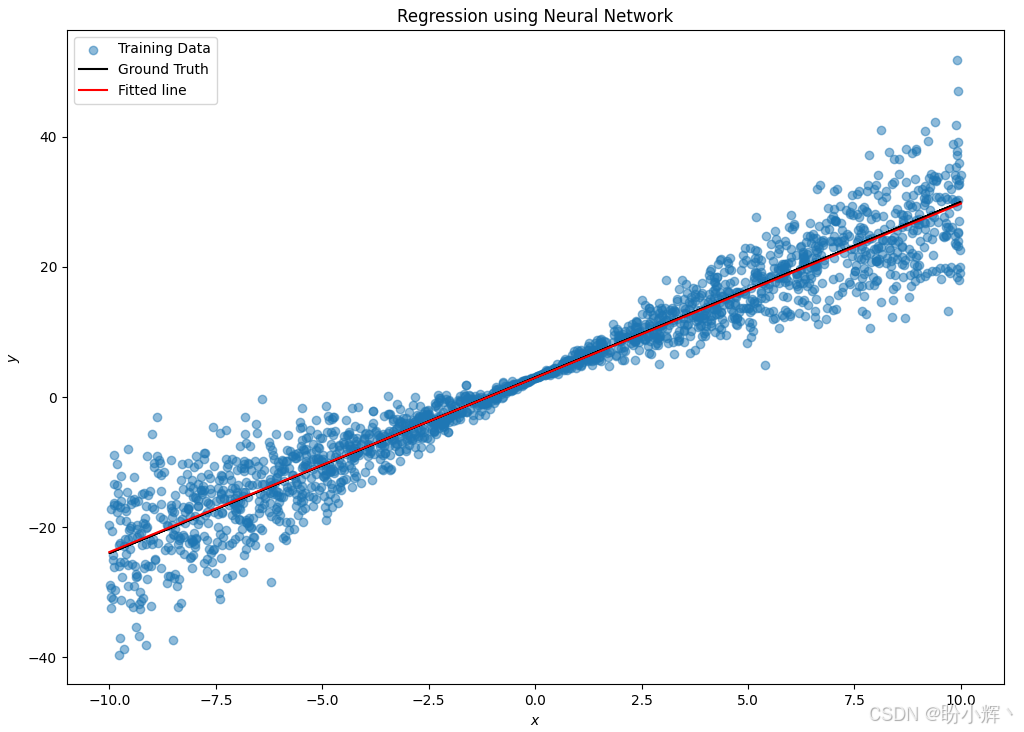
可以看到拟合的结果几乎与真实值重合，但无法确定预测的不确定性。

3. 用于偶然不确定性的概率神经网络

在合成数据集中，偶然不确定性的来源是噪声，我们知道噪声服从正态分布，由两个参数(均值和标准差)来表征。因此，可以修改模型来预测均值和标准差分布，而不是实际的 y y y 值。可以使用 IndependentNormal TFP 层或 DistributionLambda TFP 层来实现，修改后的模型如下：

python 复制代码

model = Sequential([Dense(2, input_shape = (1,)),
    tfp.layers.DistributionLambda(lambda t: tfd.Normal(loc=t[..., :1], scale=0.3+tf.math.abs(t[...,1:])))
])

之前，预测的是 y y y 值，因此使用均方误差损失，而在预测分布的情况下，更好的选择是使用负对数似然作为损失函数：

python 复制代码

# Define negative loglikelihood loss function
def neg_loglik(y_true, y_pred):
    return -y_pred.log_prob(y_true)

训练模型：

python 复制代码

model.compile(loss=neg_loglik, optimizer='adam')

# Fit
model.fit(x_train, y_train, epochs=500, verbose=2)

由于模型返回的是分布，需要测试数据集的均值和标准差统计信息：

python 复制代码

# Summary Statistics
y_mean = model(x_test).mean()
y_std = model(x_test).stddev()

需要注意的是，预测的均值对应于不考虑不确定性时的拟合线，可视化拟合结果：

python 复制代码

fig = plt.figure(figsize = (20, 10))
plt.scatter(x_train, y_train, marker='+', label='Training Data', alpha=0.5)
plt.plot(x_train, y_true, color='k', label='Ground Truth')
plt.plot(x_test, y_mean, color='r', label='Predicted Mean')
plt.fill_between(np.squeeze(x_test), np.squeeze(y_mean+1*y_std), np.squeeze(y_mean-1*y_std),  alpha=0.6, label='Aleatory Uncertainty (1SD)')
plt.fill_between(np.squeeze(x_test), np.squeeze(y_mean+2*y_std), np.squeeze(y_mean-2*y_std),  alpha=0.4, label='Aleatory Uncertainty (2SD)')
plt.title('Aleatory Uncertainty')
plt.xlabel('$x$')
plt.ylabel('$y$')
plt.legend()
plt.show()

拟合线及偶然不确定性如下所示：

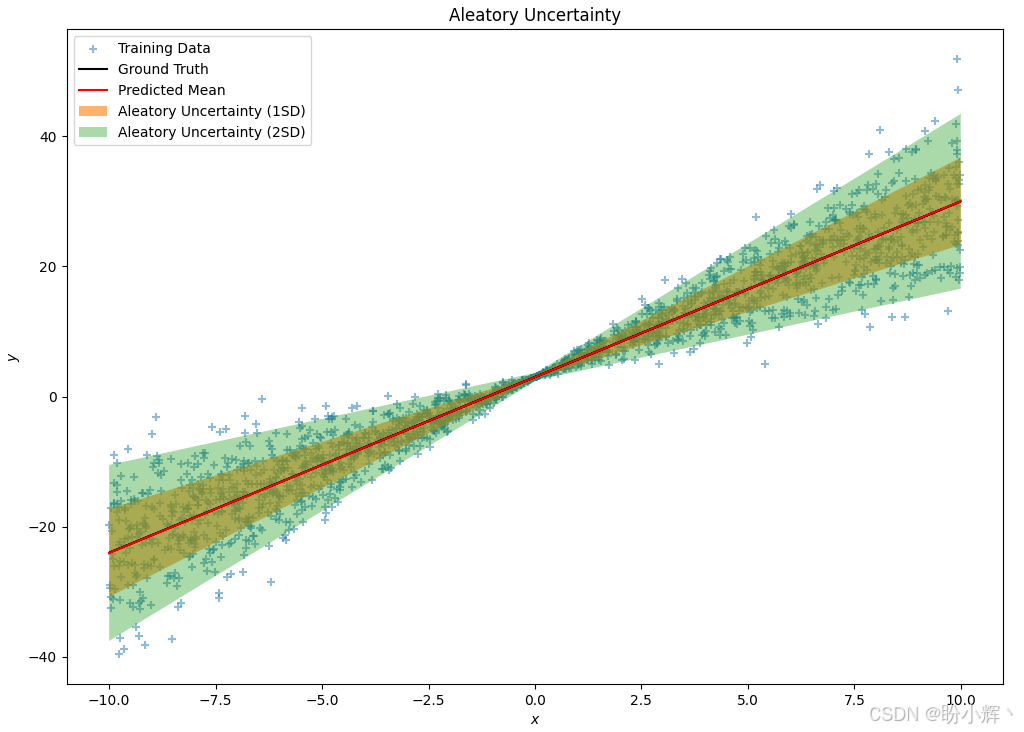
可以看到，模型在原点附近的不确定性较小，但随着离原点距离的增加，不确定性增大。

4. 认知不确定性

在传统神经网络中，每个权重由一个单一的数字表示，并且通过更新权重以最小化模型的损失，通常假设学习到的权重是最优的。为了验证学习到的权重是否是最优的，将每个权重替换为一个分布，而不是学习单一的值，模型将学习每个权重分布的一组参数，通过用 DenseVariational 层替换 Dense 层实现。DenseVariational 层使用权重的变分后验来表示其值的不确定性，它试图使后验分布接近先验分布。因此，要使用 DenseVariational 层，需要定义两个函数，一个用于生成先验分布，另一个用于生成后验分布。

模型包含两层，DenseVariational 层和 DistributionLambda 层：

python 复制代码

import tensorflow_probability as tfp
import matplotlib.pyplot as plt
import numpy as np
import tensorflow as tf
from tensorflow.keras.layers import Dense
from tensorflow.keras import Sequential

tfd = tfp.distributions

def create_dataset(n, x_range):
    x_uniform_dist = tfd.Uniform(low=x_range[0], high=x_range[1])
    x = x_uniform_dist.sample(n).numpy() [:, np.newaxis] 
    y_true = 2.7*x+3
    eps_uniform_dist = tfd.Normal(loc=0, scale=1)
    eps = eps_uniform_dist.sample(n).numpy() [:, np.newaxis] *0.74*x
    y = y_true + eps
    return x, y, y_true

x_train, y_train, y_true = create_dataset(200, [-10, 10])
x_val, y_val, _ = create_dataset(50, [-10, 10])

def posterior_mean_field(kernel_size, bias_size=0, dtype=None):
    n = kernel_size + bias_size
    c = np.log(np.expm1(1.))
    return Sequential([
        tfp.layers.VariableLayer(2 * n, dtype=dtype),
        tfp.layers.DistributionLambda(lambda t: tfd.Independent(
            tfd.Normal(loc=t[..., :n],
                        scale=1e-5 + tf.nn.softplus(c + t[..., n:])),
            reinterpreted_batch_ndims=1)),
    ])

def prior_trainable(kernel_size, bias_size=0, dtype=None):
    n = kernel_size + bias_size
    return Sequential([
        tfp.layers.VariableLayer(n, dtype=dtype),
        tfp.layers.DistributionLambda(lambda t: tfd.Independent(
            tfd.Normal(loc=t, scale=1),
            reinterpreted_batch_ndims=1)),
    ])

negloglik = lambda y, rv_y: -rv_y.log_prob(y)

# Build model.
model = Sequential([
        tfp.layers.DenseVariational(1, posterior_mean_field, prior_trainable, kl_weight=1/x_train.shape[0]),
        tfp.layers.DistributionLambda(lambda t: tfd.Normal(loc=t, scale=1)),
])

同样，由于寻找的是分布，因此使用的损失函数是负对数似然函数：

python 复制代码

model.compile(optimizer=tf.optimizers.Adam(learning_rate=0.01), loss=negloglik)

使用合成数据进行模型训练：

python 复制代码

model.fit(x_train, y_train, epochs=100, verbose=2)

x_range = [-10, 10]
plt.figure(figsize=[10, 10]) 
plt.clf();
plt.plot(x_train, y_train, 'b.', label='observed');

y_preds = [model(x_val) for _ in range(100)]
avgm = np.zeros_like(x_val[..., 0])
for i, yhat in enumerate(y_preds):
    m = np.squeeze(yhat.mean())
    s = np.squeeze(yhat.stddev())
    if i < 15:
        plt.plot(x_val, m, 'r', label='ensemble means' if i == 0 else None, linewidth=0.5)
    avgm += m
plt.plot(x_val, avgm/len(y_preds), 'g', label='overall mean', linewidth=4)
plt.xticks(fontsize=20)
plt.yticks(fontsize=20)
plt.legend(loc='upper left', prop={'size': 20})
plt.show()

模型训练完成后，进行预测，为了理解不确定性概念，对相同输入范围进行多次预测，可以在下图中看到结果的方差差异：

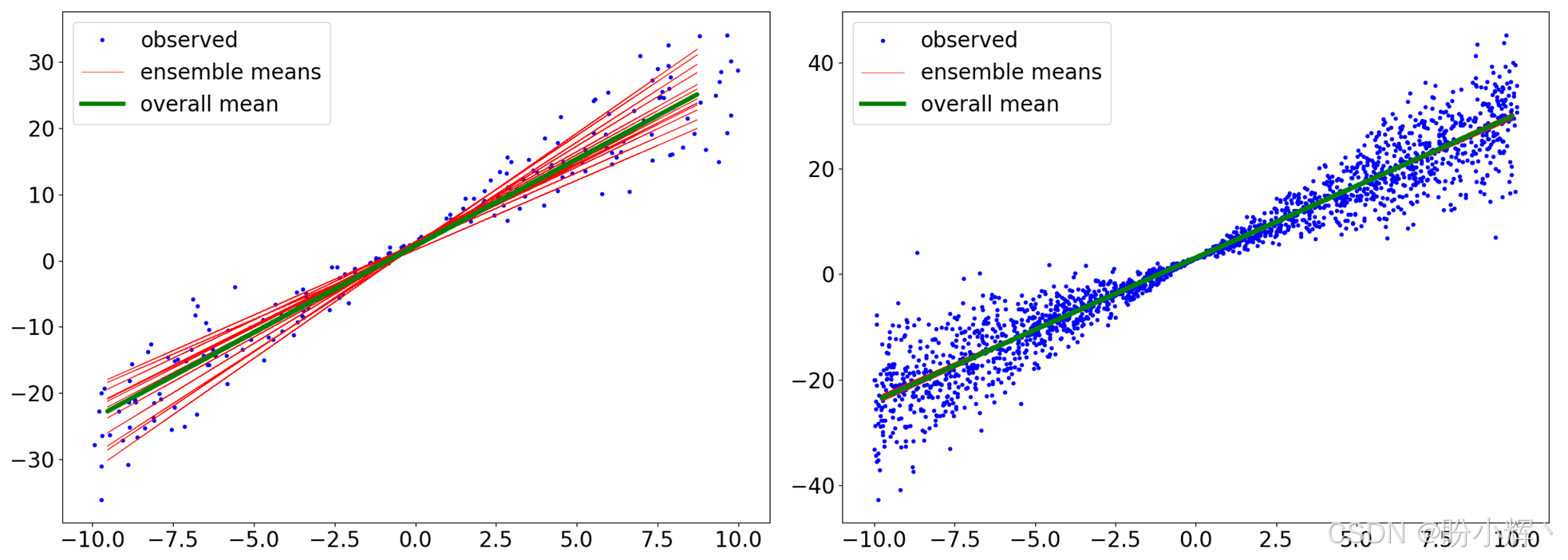
上图包含两个子图，一个是使用 200 个训练数据点训练的模型，另一个是使用 2,000 个数据点训练的模型。可以看到，当数据量更多时，方差和认知不确定性会减少。其中，overall mean 指的是所有预测的均值 (100 个)，而 ensemble means 仅考虑了前 15 个预测。所有机器学习模型在预测结果时都存在一定程度的不确定性。获取不确定性的估计或可量化范围能够帮助用户对神经网络预测建立更大的信心，并推动人工智能更广泛的应用。

小结

本节介绍了介绍了概率推理的必要性------由于数据的固有特性和缺乏知识而产生的不确定性。介绍了如何构建贝叶斯网络并进行推理，接着，使用 TFP 网络层构建了贝叶斯神经网络，以考虑偶然不确定性。最后，学习了如何利用 DenseVariational TFP 层来考虑认知不确定性。

系列链接