如果你是一名刚接触大语言模型(LLM)的初学者,很可能会在社交媒体上看到这样一个项目------MiniMind

这个项目实现了一个参数规模较小但功能完整的 LLM,涵盖了预训练、LoRA 微调、SFT、蒸馏以及基于人类反馈的强化学习(RLHF)等多个模块,可以说是非常难得的入门教材。
MiniMind 提供了清晰的复现指南和环境配置说明,但在代码背后的原理解释上并不算详细。对于像笔者这样并非 NLP 出身的初学者来说,直接啃源码还是有相当的难度,因此有必要把一些关键的基础知识梳理下来,既能帮助加深理解,也便于后续复习。
因此,本文主要记录了笔者在学习该项目过程中新掌握或重新温习的重要知识点,并在文末推荐了一些适合入门的参考博客。同时,文中还附上了带注释的源码片段,希望能为理解整个项目的实现提供更直观的帮助。
RMSNorm
现在LLM架构或者其他transfomer架构喜欢使用RMSNorm,我们在这里一并区分三种常见的Norm:
BatchNorm(for cv)
BatchNorm,是按照batch维度进行归一化。常用于CV任务, BatchNorm把一个batch中同一通道的所有特征(如下图红色通道对应特征图)视为一个分布(有几个通道就有几个分布),并将其标准化。
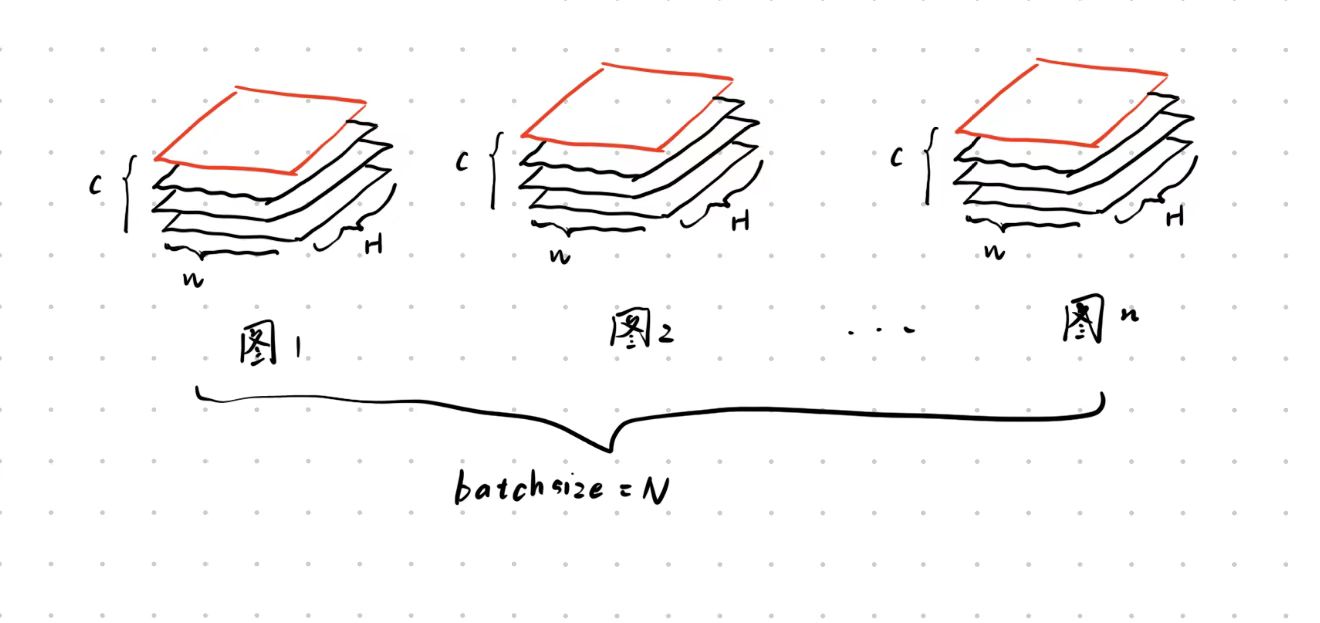
代码:一个batchsize的数据送入网络,经过卷积层,得到一个四维的tensor,形状为(batch_size, channels, height, width),即(N,C,H,W)然后对这个tensor进行BatchNorm操作。
假设输入张量形状是:
\[x \in \mathbb{R}^{(N, C, H, W)} \]
- \(N\):batch size
- \(C\):通道数(channel)
- \(H, W\):空间维度(height, width)
对每个通道 \(c\),在整个 batch(N 个样本,H×W 个位置)上统计均值和方差,然后做标准化。
对于通道 \(c\),我们先算均值和方差:
\[\mu_c = \frac{1}{N \cdot H \cdot W} \sum_{n=1}^N \sum_{h=1}^H \sum_{w=1}^W x_{n,c,h,w} \]
\[\sigma_c^2 = \frac{1}{N \cdot H \cdot W} \sum_{n=1}^N \sum_{h=1}^H \sum_{w=1}^W (x_{n,c,h,w} - \mu_c)^2 \]
然后标准化:
\[\hat{x}{n,c,h,w} = \frac{x{n,c,h,w} - \mu_c}{\sqrt{\sigma_c^2 + \epsilon}} \]
最后再加上可学习的缩放和平移参数:
\[y_{n,c,h,w} = \gamma_c \hat{x}_{n,c,h,w} + \beta_c \]
其中:
- \(\gamma_c, \beta_c\) 是学习到的参数(每个通道一对)。
- \(\epsilon\) 是防止除零的常数。
手动实现:
python
import torch
def batchnorm2d(x, gamma, beta, eps=1e-5):
# x: [8,3,32,32]
mean = x.mean(dim=(0, 2, 3), keepdim=True) # mean: [1,3,1,1]
var = x.var(dim=(0, 2, 3), keepdim=True, unbiased=False) # var: [1,3,1,1]
x_hat = (x - mean) / torch.sqrt(var + eps) # 标准化,x_hat: [8,3,32,32],mean,var从[1,3,1,1] 广播为[8,3,32,32]
y = gamma.view(1, -1, 1, 1) * x_hat + beta.view(1, -1, 1, 1)
return y
# 测试
x = torch.randn(8, 3, 32, 32) # batch=8, 通道=3, 32x32
gamma = torch.ones(3) # 初始缩放
beta = torch.zeros(3) # 初始平移
y = batchnorm2d(x, gamma, beta)
print(y.shape) # torch.Size([8, 3, 32, 32])调库实现
python
import torch
import torch.nn as nn
batch_size, channels, height, width = 8, 3, 32, 32
# 创建一个BatchNorm层,只需要指定通道数
batch_norm = nn.BatchNorm2d(channels)
input_tensor = torch.randn(batch_size, channels, height, width)
output_tensor = batch_norm(input_tensor)
print(output_tensor.shape) # 输出形状仍然是 (batch_size, channels, height, width)多提一嘴:复习广播机制:
- 如果有一个维度是 1,可以扩展到另一个维度的大小。
- 如果维度不相等,且没有 1,那么报错。
- 赋值原则:若从(1,x,y,1)扩展到(a,x,y,b),则(1,x,y,1)的值会被复制a*b次
Layernorm (for nlp)
先明确一下nlp处理的tensor形状是什么,nlp中常用的输入形状是(batch_size, seq_length, embedding_dim),即(N, L, D),其中N是batch size(几个句子),L是序列长度(一个句子多少个token),D是每个词的嵌入维度。
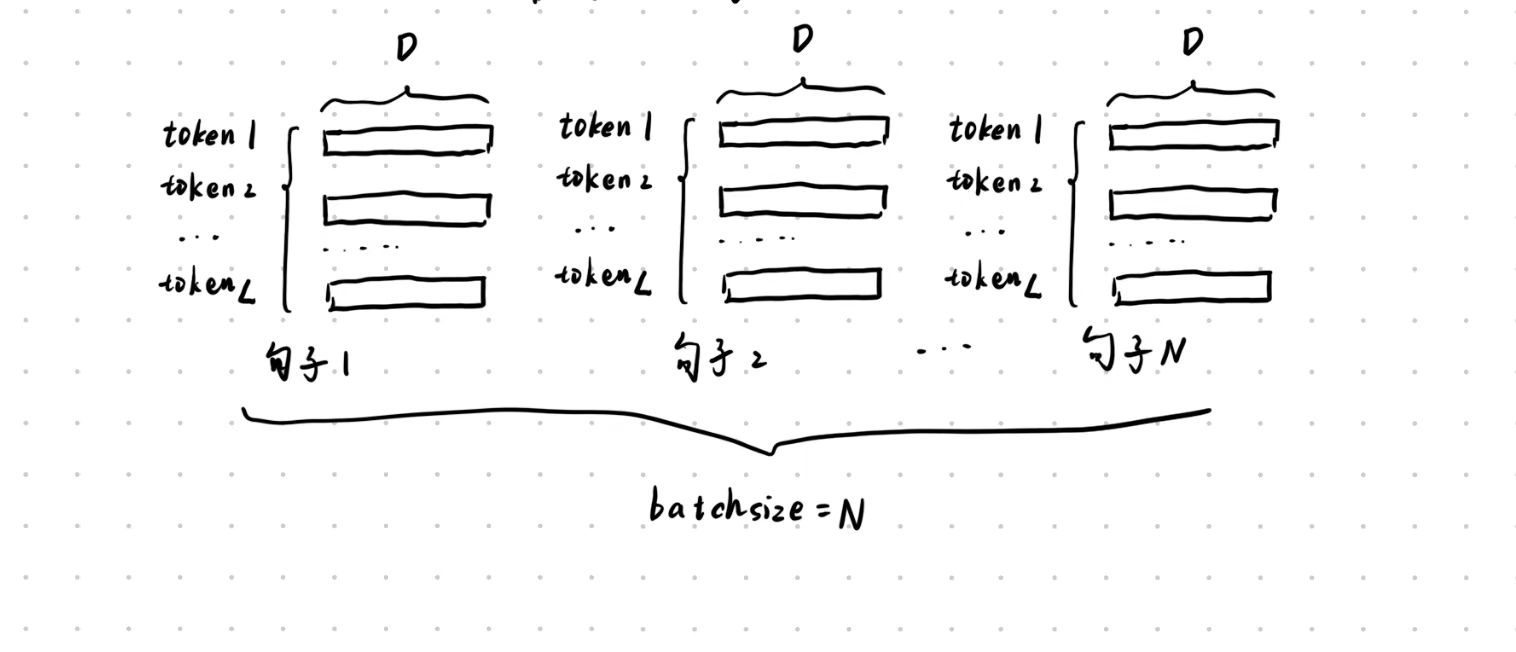
LayerNorm是对每个句子的所有词向量进行归一化。也就是每一个Embedding进行归一化,这样做的目的是保证了每个 token 的表示数值稳定,不会因为 embedding 的绝对大小不同而影响训练。
假设有一个 batch ,里面有 \(N\) 个句子,每个句子有 \(M\) 个 token,每个 token 的 embedding 维度是 \(H\):
\[x \in \mathbb{R}^{N \times M \times H} \]
LayerNorm 不会跨样本,不会跨 token 。它只会对 每个 token 的 hidden 维度 \(H\) 求均值方差。数学上,如果第 \(n\) 个句子、第 \(m\) 个 token 的 embedding 是
\[x_{n,m,:} = (x_{n,m,1}, x_{n,m,2}, \dots, x_{n,m,H}) \]
那么 LN 的均值和方差是:
\[\mu_{n,m} = \frac{1}{H}\sum_{i=1}^H x_{n,m,i}, \quad \sigma_{n,m}^2 = \frac{1}{H}\sum_{i=1}^H (x_{n,m,i}-\mu_{n,m})^2 \]
然后归一化:
\[\hat{x}{n,m,i} = \frac{x{n,m,i} - \mu_{n,m}}{\sqrt{\sigma_{n,m}^2+\epsilon}} \]
再乘上可学习参数:
\[y_{n,m,i} = \gamma_i \hat{x}_{n,m,i} + \beta_i \]
调库实现
python
import torch
import torch.nn as nn
N, M, H = 2, 4, 6 # batch=2, seq_len=4, hidden=6
x = torch.randn(N, M, H)
layernorm = nn.LayerNorm(H) # 只对最后一维 hidden 归一化
y = layernorm(x)
print("输入形状:", x.shape) # (2,4,6)
print("输出形状:", y.shape) # (2,4,6)手写
python
def layernorm(x, gamma, beta, eps=1e-5):
# x: [N, M, H]
mean = x.mean(dim=-1, keepdim=True) # [N, M, 1] 逐样本逐序列求均值
var = x.var(dim=-1, keepdim=True, unbiased=False) # [N, M, 1] 方差
x_hat = (x - mean) / torch.sqrt(var + eps) # [N, M, H] 标准化
y = gamma * x_hat + beta # [N, M, H] 缩放平移
return yRMSNorm
RMSNorm 干脆 不要均值减法,只用平方均值 (Root Mean Square, RMS):
\[\mathrm{RMSNorm}(x)=\frac x{\mathrm{RMS}(x)}\cdot\gamma \]
其中
\[\mathrm{RMS}(x)=\sqrt{\frac1d\sum_{i=1}^dx_i^2+\epsilon} \]
在Minimind的代码中,实现如下:
python
class RMSNorm(torch.nn.Module):
def __init__(self, dim: int, eps: float = 1e-5):
super().__init__()
self.eps = eps
self.weight = nn.Parameter(torch.ones(dim)) # 可学习的权重参数gamma
def _norm(self, x):
return x * torch.rsqrt(x.pow(2).mean(-1, keepdim=True) + self.eps) # rsqrt:reciprocal square root 倒数平方根运算
def forward(self, x):
return self.weight * self._norm(x.float()).type_as(x) # 确保类型一致
RoPE
RoPE (Rotary Position Embedding) 是一种位置编码方法,旨在为 Transformer 模型引入位置信息。与传统的绝对位置编码(如正弦余弦位置编码)不同,RoPE 通过对查询(Q)和键(K)向量进行旋转变换来实现相对位置编码。
定义二位旋转矩阵:
\[\boldsymbol{f}(\boldsymbol{q},m)=\binom{\cos m\theta\quad-\sin m\theta}{\sin m\theta\quad\cos m\theta}\left(\frac{q_0}{q_1}\right) \]
由于内积满足线性叠加性,因此任意偶数维的RoPE,我们都可以表示为二维情形的拼接,即
\[\underbrace{\begin{pmatrix}\cos m\theta_{0}&-\sin m\theta_{0}&0&0&\cdots&0&0\\\sin m\theta_{0}&\cos m\theta_{0}&0&0&\cdots&0&0\\0&0&\cos m\theta_{1}&-\sin m\theta_{1}&\cdots&0&0\\0&0&\sin m\theta_{1}&\cos m\theta_{1}&\cdots&0&0\\\vdots&\vdots&\vdots&\vdots&\ddots&\vdots&\vdots\\0&0&0&0&\cdots&\cos m\theta_{d/2-1}&-\sin m\theta_{d/2-1}\\0&0&0&0&\cdots&\sin m\theta_{d/2-1}&\cos m\theta_{d/2-1}\end{pmatrix}}{\mathbf{a}{m}}\begin{pmatrix}q_{0}\\q_{1}\\q_{2}\\q_{3}\\\vdots\\q_{d-2}\\q_{d-1}\end{pmatrix} \]
也就是说,给位置为\(m\)的向量\(q\)乘上矩阵\(\mathcal{R}_m\)、位置为\(\color{red}{n}\)的向量\(k\)乘上矩阵\(\mathcal{R}_n\),用变换后的\(Q,K\)序列
做Attention,那么Attention就自动包含相对位置信息了,因为成立恒等式:
\[(\mathcal{R}_m\boldsymbol{q})^\top(\mathcal{R}_n\boldsymbol{k})=\boldsymbol{q}^\top\mathcal{R}_m^\top\mathcal{R}n\boldsymbol{k}=\boldsymbol{q}^\top\mathcal{R}{n-m}\boldsymbol{k} \]
鉴于计算中的稀疏性,直接用矩阵乘法来实现会很浪费算力,推荐通过下述方式来实现RoPE:
\[\begin{pmatrix}q_0\\q_1\\q_2\\q_3\\\vdots\\q_{d-2}\\q_{d-1}\end{pmatrix}\otimes\begin{pmatrix}\cos m\theta_0\\\cos m\theta_0\\\cos m\theta_1\\\cos m\theta_1\\\vdots\\\cos m\theta_{d/2-1}\\\cos m\theta_{d/2-1}\end{pmatrix}+\begin{pmatrix}-q_1\\q_0\\-q_3\\q_2\\\vdots\\-q_{d-1}\\q_{d-2}\end{pmatrix}\otimes\begin{pmatrix}\sin m\theta_0\\\sin m\theta_0\\\sin m\theta_1\\\sin m\theta_1\\\vdots\\\sin m\theta_{d/2-1}\\\sin m\theta_{d/2-1}\end{pmatrix} \]
最后说一下\(\theta\)的取值,代码里面\(\theta_i\)记为了\(\omega_i\):
先构造频率
\[\omega_i=\frac1{\theta^{i/d}},\quad i=0,2,4,\ldots,dim-2 \]
一共 dim/2 个不同的频率。然后乘以位置 \(m\):
\[\text{freqs}[m,i]=m\cdot\omega_i \]
这就对应到公式里的 \(m\theta_i\)。换句话说,freqs 里面存的就是 角度 \(m\theta_i\)。
Minimind的代码实现:
python
def precompute_freqs_cis(dim: int, end: int = int(32 * 1024), theta: float = 1e6):
# 计算所有维度位置的频率
freqs = 1.0 / (theta ** (torch.arange(0, dim, 2)[: (dim // 2)].float() / dim))
# 不同位置的q,k向量乘不同的m,这里生成0,1,2,...,end-1
t = torch.arange(end, device=freqs.device)
# 外积得到(end, dim/2) 第i行对应适用于token位置i的q,k
freqs = torch.outer(t, freqs).float()
# 计算cos和sin,并拼接成(end, dim)
freqs_cos = torch.cat([torch.cos(freqs), torch.cos(freqs)], dim=-1)
freqs_sin = torch.cat([torch.sin(freqs), torch.sin(freqs)], dim=-1)
return freqs_cos, freqs_sin
def apply_rotary_pos_emb(q, k, cos, sin, position_ids=None, unsqueeze_dim=1):
def rotate_half(x):
return torch.cat((-x[..., x.shape[-1] // 2:], x[..., : x.shape[-1] // 2]), dim=-1)
q_embed = (q * cos.unsqueeze(unsqueeze_dim)) + (rotate_half(q) * sin.unsqueeze(unsqueeze_dim))
k_embed = (k * cos.unsqueeze(unsqueeze_dim)) + (rotate_half(k) * sin.unsqueeze(unsqueeze_dim))
return q_embed, k_embedGQA-attention
在梳理Attention模块的的代码实现之前,我们需要提前认知几个重要概念,并做一些回顾:
torch操作回顾
- 在 PyTorch 里,@ 和 torch.matmul 对高维张量矩阵乘法的定义是:只取最后两个维度做矩阵乘法!
python
A.shape = [2, 3, 4, 5] # (batch=2, heads=3, 4×5矩阵)
B.shape = [2, 3, 5, 6] # (batch=2, heads=3, 5×6矩阵)
C = A @ B # [2, 3, 4, 6]- 对高维张量,transpose(dim1, dim2) 只会交换这两个维度,其他维度保持不变。(注意,dim从前往后数是0开始的,使用负数的时候,-1 表示最后一维,-2 表示倒数第二维)
python
A.shape = [2, 3, 4, 5] # (batch=2, heads=3, 4×5矩阵)
B = A.transpose(1, 2) # 交换第1维和第2维
B.shape # [2, 4, 3, 5]
x = torch.randn(2, 3, 4, 5) # shape = (2, 3, 4, 5)
y = x.transpose(-1, -3) # 相当于 transpose(3, 1)
print(y.shape) # (2, 5, 4, 3)nn.Linear本质上也是矩阵乘法,当高维 tensor 输入 linear 层时,只有最后两个维度会参与线性计算,前面的维度会被视为 batch 维度而保留下来。例如:
python
proj = nn.Linear(args.hidden_size, args.num_attention_heads * self.head_dim, bias=False)如果输入的形状是 (bsz, seq_len, hidden_size),经过 proj 之后会变成 (bsz, seq_len, num_attention_heads * head_dim)。这里的线性层相当于对每个 token 的隐状态向量做一次相同的全连接变换,把它映射到多头注意力所需的维度空间。
kv-cache
一种缓存机制,用于加速推理过程。鉴于计算注意力得分的时候,key和value需要被复用,因此可以缓存之前的key和value,空间换时间。
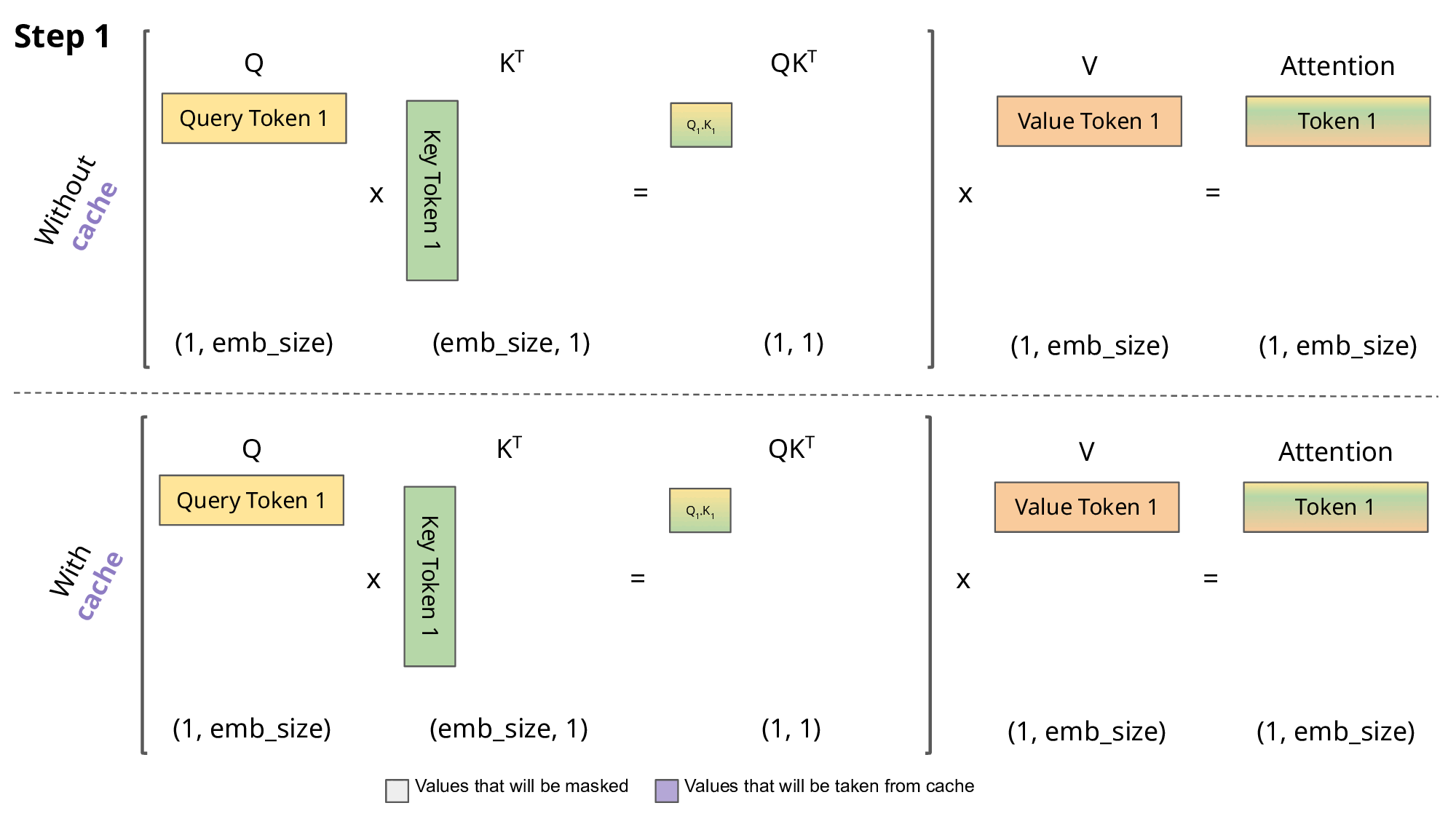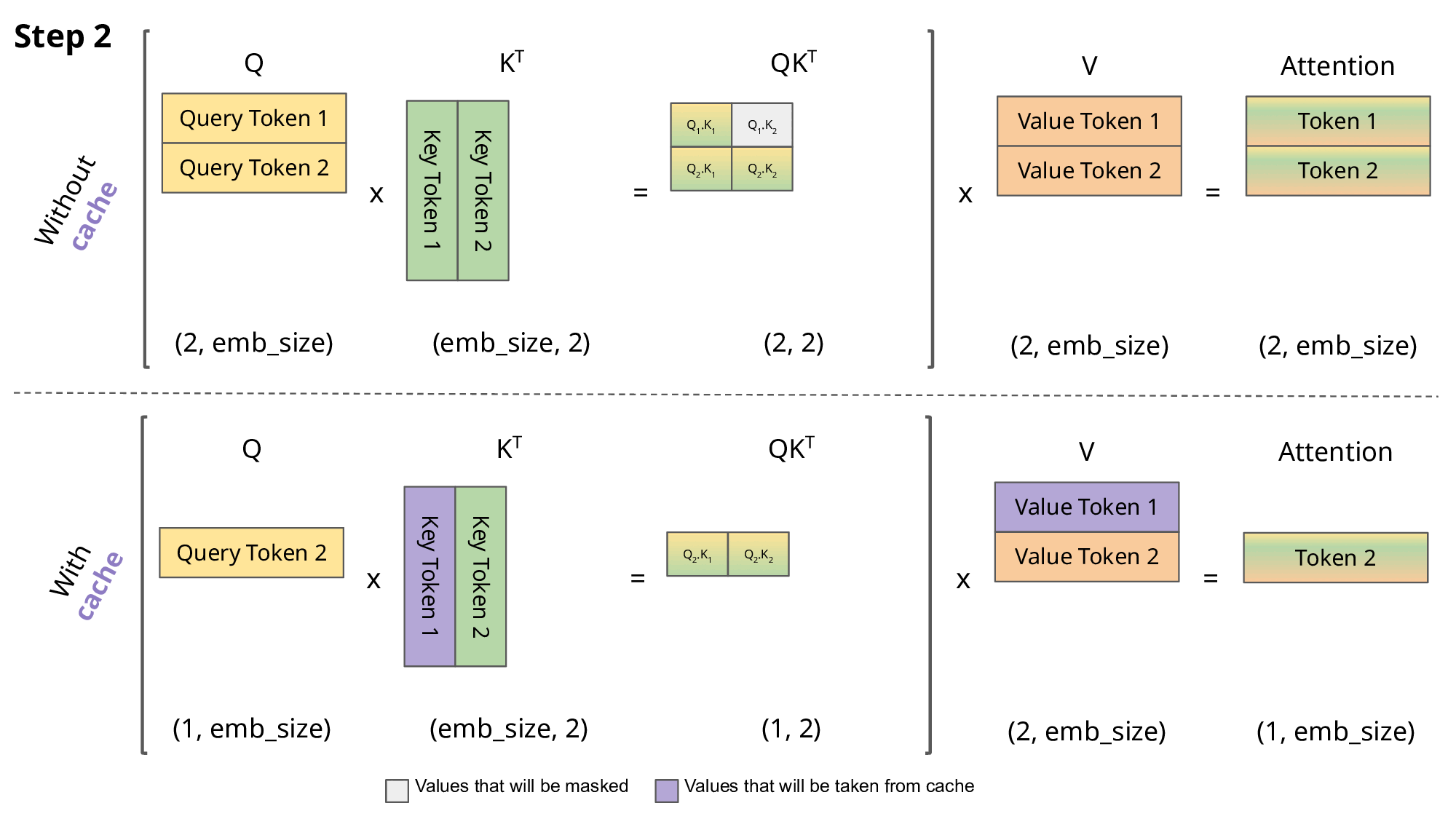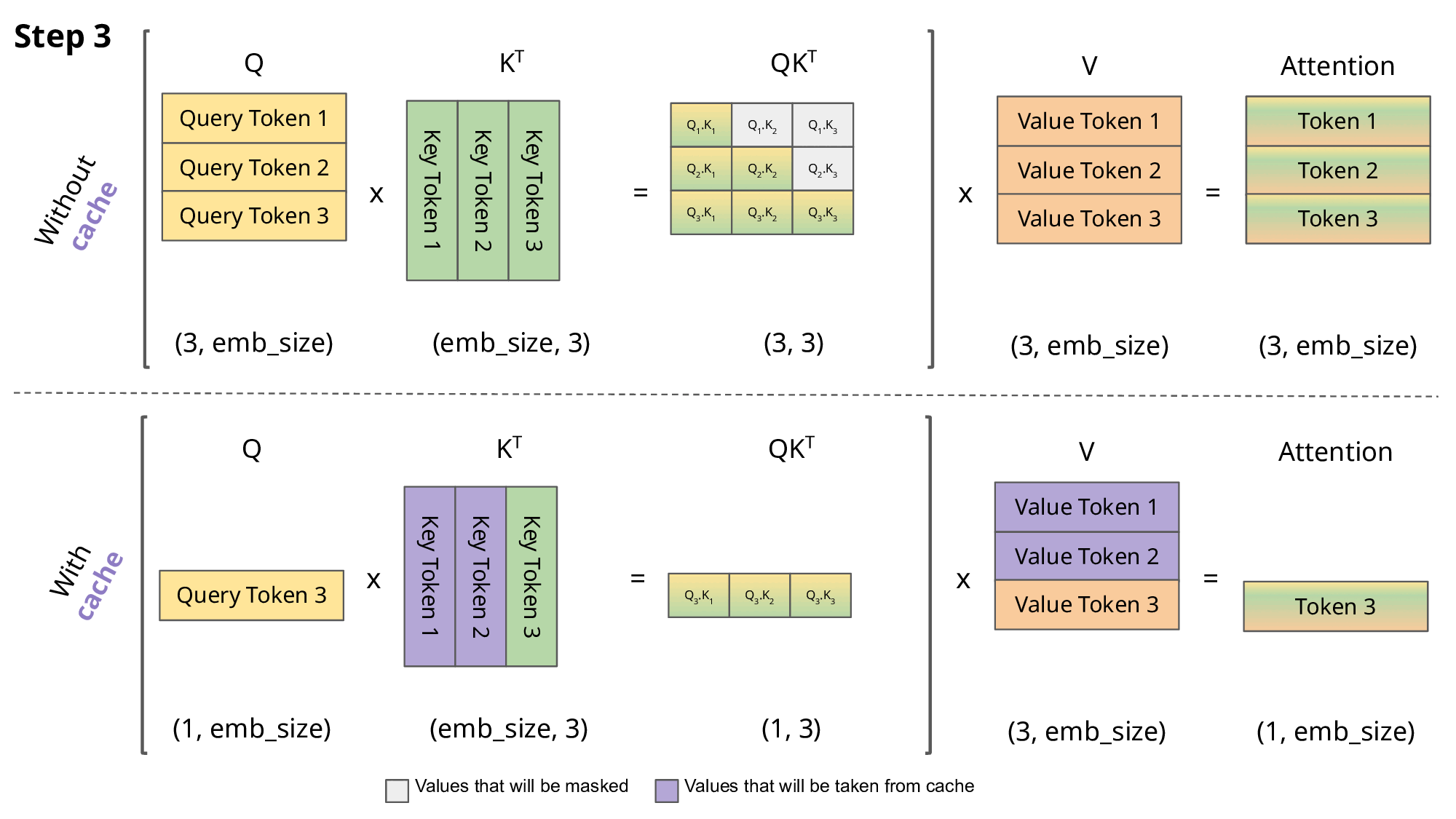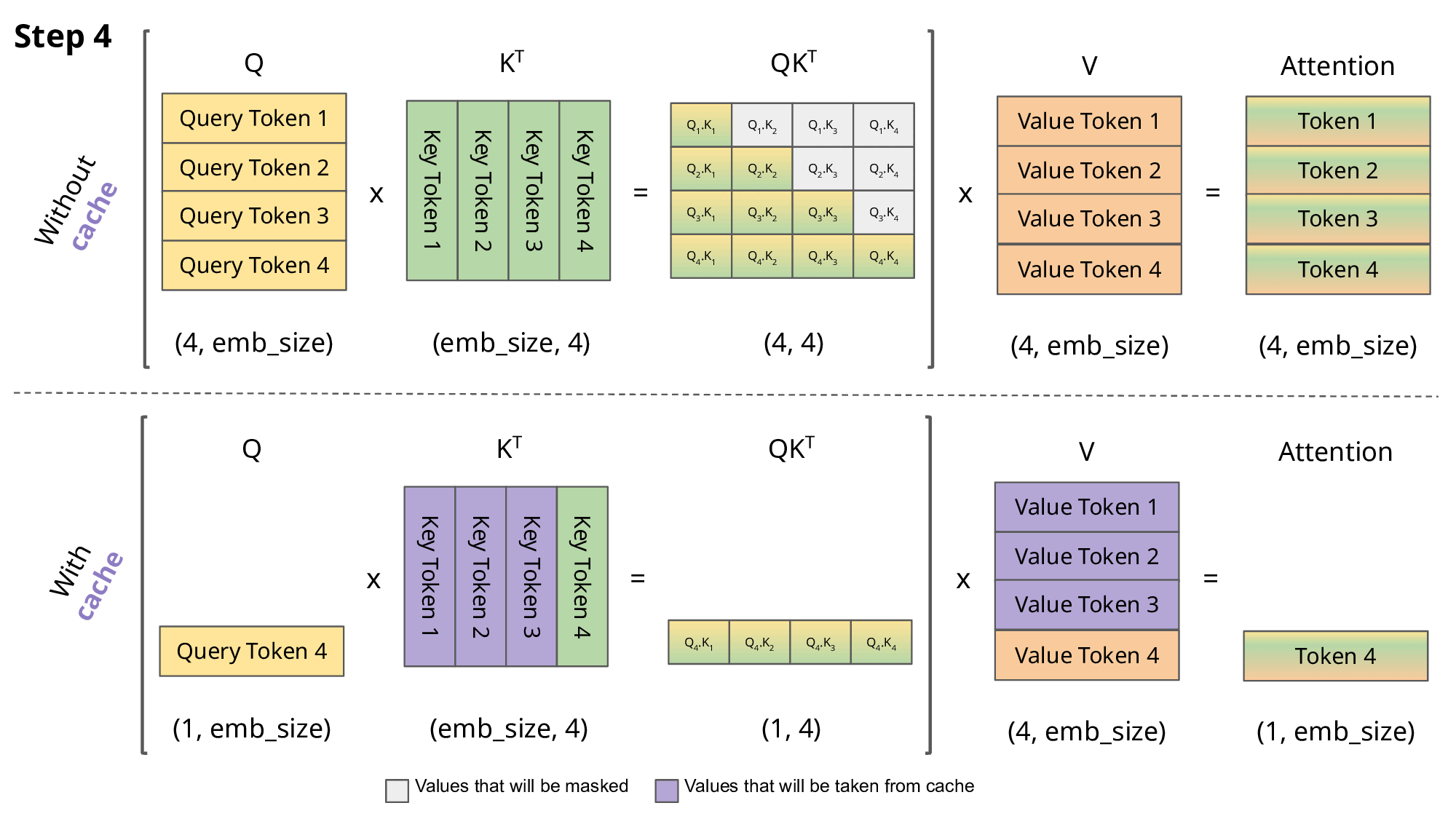
python
# kv_cache实现,推理时使用,训练时关闭
if past_key_value is not None:
xk = torch.cat([past_key_value[0], xk], dim=1)
xv = torch.cat([past_key_value[1], xv], dim=1)
past_kv = (xk, xv) if use_cache else Nonemask操作
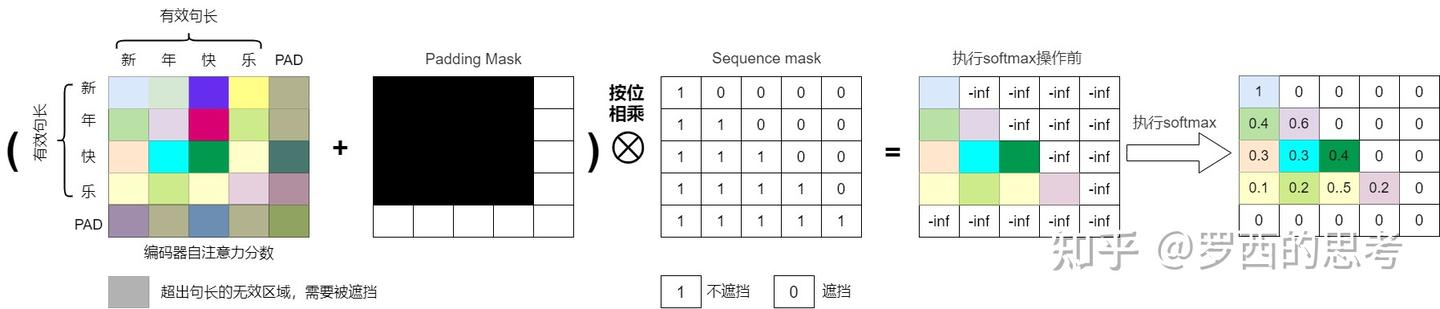
推荐一个写的很不错的博客:https://zhuanlan.zhihu.com/p/28786272137
因果mask:(Causal Mask,下三角)
- Q/K/V的形状: (bsz, num_heads, seq_len, head_dim)
- 转置后形状:(bsz, self.n_local_heads, seq_len, self.head_dim)
矩阵乘法默认发生在最后两个维度上,因此 Q @ K^T 的结果形状是 (bsz, num_heads, seq_len, seq_len),表示一个bsz中,每个head的每个query与所有key的相似度得分。
因果mask矩阵作用在(seq_len, seq_len)维度上,确保每个位置只能看到它之前(包括它自己)的token。具体的,每个待处理token之后的位置被设置为负无穷(-inf),这样在softmax之后,这些位置的权重就变成了0。
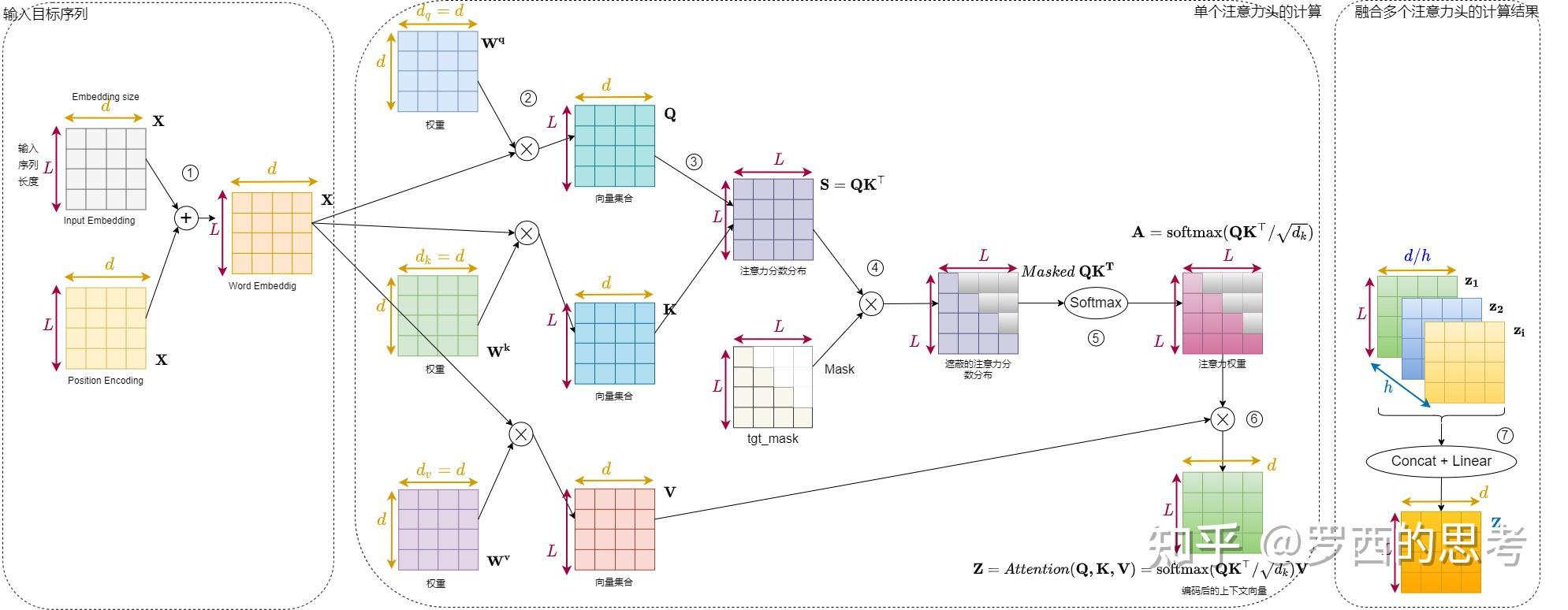
padding mask
在神经网络的训练过程中,同一个batch会包含有多个文本序列,不同的序列长度并不一定会一致。而神经网络的输入需要一个规整的张量。为了符合模型的输入方式,在数据集的生成过程中,我们要对输入序列进行对齐,使同一个batch内所有序列的长度一致。具体来说就是:
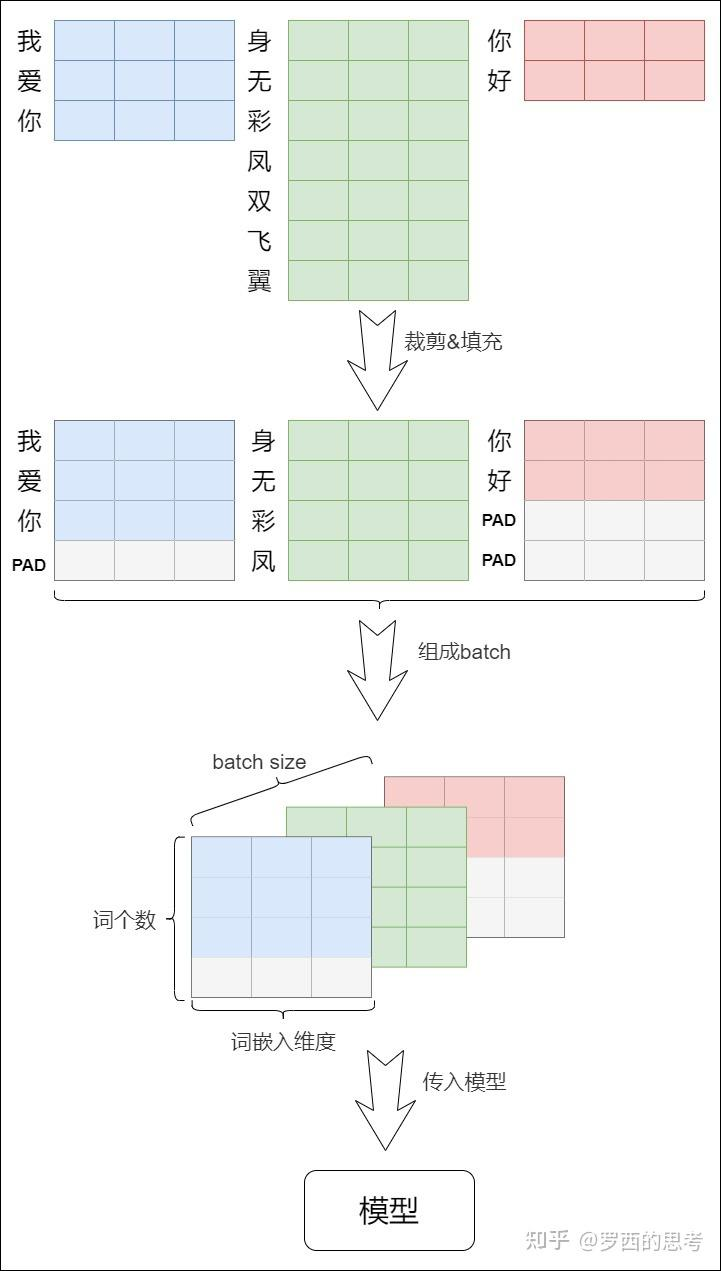
因此,综合考虑两种mask,我们可以将它们相加,得到最终的注意力掩码矩阵。这个矩阵会在计算注意力得分时使用,确保模型只能关注到合法的位置。
完整代码解析+注释
现在,我们进行源代码的逐行解析,在看代码之前,我们先明确一下Dense model涉及到的所有参数
| 模块 | 参数名 | 含义 | 典型值 | 备注 |
|---|---|---|---|---|
| GQA (Grouped Query Attention) | hidden_size |
输入 embedding 维度 | 512 | Q/K/V 输入输出的基准维度 |
num_attention_heads |
Q 的头数 | 8 | Query 被分成多少个子空间 | |
num_key_value_heads |
KV 的头数 | 2 | K/V 使用更少的头数,节省显存 | |
head_dim |
每个头的维度 | hidden_size // num_attention_heads = 64 |
Q/K/V 每个头的子空间大小 | |
n_rep |
Q 头 / KV 头比值 | num_attention_heads // num_key_value_heads = 4 |
每个 KV 头复制给多个 Q 头 | |
| FFN (Feed-Forward Network) | hidden_size |
输入维度 | 512 | 与 Transformer 输入输出一致 |
intermediate_size |
中间层维度 | 通常 hidden_size * 4 = 2048 |
扩展后再压缩 | |
hidden_act |
激活函数 | SiLU | 典型是 ReLU / GELU / SiLU |
|
dropout |
Dropout 比例 | 0.0 | 防止过拟合 |
简写几个关键变量:
batch_size = bszseq_len = Lhidden_size = 512num_attention_heads = 8num_key_value_heads = 2head_dim = 64
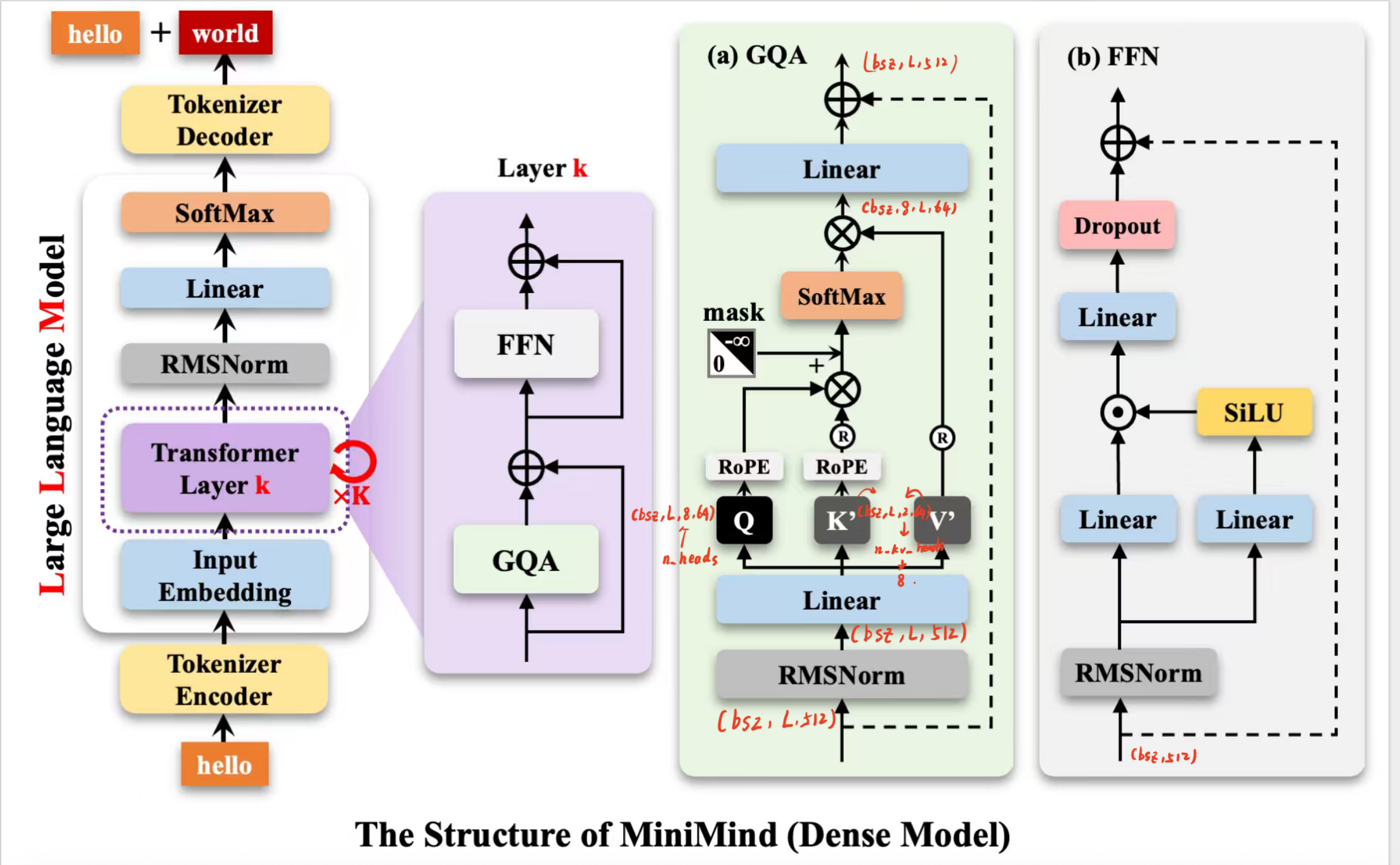
现在可以看Attention部分的源代码了,我做了详细的注释
python
class Attention(nn.Module):
def __init__(self, args: MiniMindConfig):
super().__init__()
# GQA 中 q的头数可以多于kv的头数,因此先做一个判断
self.num_key_value_heads = args.num_attention_heads if args.num_key_value_heads is None else args.num_key_value_heads
assert args.num_attention_heads % self.num_key_value_heads == 0 # 确保q的头数是kv头数的整数倍
self.n_local_heads = args.num_attention_heads # Q 的头数
self.n_local_kv_heads = self.num_key_value_heads # K/V 的头数
self.n_rep = self.n_local_heads // self.n_local_kv_heads # Q头数 / KV头数,表示每个KV头会被复制给多少个Q头
self.head_dim = args.hidden_size // args.num_attention_heads # 每个头的维度,即原始Embedding压缩后的维度 (一般这种压缩满足:原始hidden_size = num_heads * head_dim)
self.q_proj = nn.Linear(args.hidden_size, args.num_attention_heads * self.head_dim, bias=False) # W_q,多头已经并起来了
self.k_proj = nn.Linear(args.hidden_size, self.num_key_value_heads * self.head_dim, bias=False) # W_k,多头已经并起来了
self.v_proj = nn.Linear(args.hidden_size, self.num_key_value_heads * self.head_dim, bias=False) # W_v,多头已经并起来了
self.o_proj = nn.Linear(args.num_attention_heads * self.head_dim, args.hidden_size, bias=False) # 输出投影,把多头结果线性组合(变换)为原始hidden_size维度
self.attn_dropout = nn.Dropout(args.dropout) # 注意力得分的dropout
self.resid_dropout = nn.Dropout(args.dropout) # 输出的dropout
self.dropout = args.dropout # 用于flash attention的dropout
self.flash = hasattr(torch.nn.functional, 'scaled_dot_product_attention') and args.flash_attn # 检查是否能用flash attention这一高效实现,如果可以则self.flash = True
# print("WARNING: using slow attention. Flash Attention requires PyTorch >= 2.0")
# x的输入形状: (bsz, seq_len, hidden_size)
def forward(self,
x: torch.Tensor,
position_embeddings: Tuple[torch.Tensor, torch.Tensor], # 修改为接收cos和sin
past_key_value: Optional[Tuple[torch.Tensor, torch.Tensor]] = None,
use_cache=False, # 训练时关闭,推理时打开
attention_mask: Optional[torch.Tensor] = None # (bsz, seq_len) 1表示有效,0表示padding(后续转化为False,用于mask)
) -> Tuple[torch.Tensor, Optional[Tuple[torch.Tensor, torch.Tensor]]]:
bsz, seq_len, _ = x.shape
xq, xk, xv = self.q_proj(x), self.k_proj(x), self.v_proj(x)
xq = xq.view(bsz, seq_len, self.n_local_heads, self.head_dim)
xk = xk.view(bsz, seq_len, self.n_local_kv_heads, self.head_dim)
xv = xv.view(bsz, seq_len, self.n_local_kv_heads, self.head_dim)
cos, sin = position_embeddings
xq, xk = apply_rotary_pos_emb(xq, xk, cos[:seq_len], sin[:seq_len]) #(应用RoPE后)
# kv_cache实现,推理时使用,训练时关闭
if past_key_value is not None:
xk = torch.cat([past_key_value[0], xk], dim=1)
xv = torch.cat([past_key_value[1], xv], dim=1)
past_kv = (xk, xv) if use_cache else None
# repeat k,v的头数与q匹配
# 转置:(bsz, seq_len, self.n_local_heads, self.head_dim) -> (bsz, self.n_local_heads, seq_len, self.head_dim)
xq, xk, xv = (
xq.transpose(1, 2),
repeat_kv(xk, self.n_rep).transpose(1, 2),
repeat_kv(xv, self.n_rep).transpose(1, 2)
)
# 如果可以使用flash attention
if self.flash and seq_len != 1:
# 训练时打开 dropout,推理时关闭
dropout_p = self.dropout if self.training else 0.0
attn_mask = None
if attention_mask is not None: # 有padding mask
attn_mask = attention_mask.view(bsz, 1, 1, -1).expand(bsz, self.n_local_heads, seq_len, -1) # bsz, self.n_local_heads, seq_len, seq_len
attn_mask = attn_mask.bool() if attention_mask is not None else None # 转0,1为bool,符合flash attention的要求
output = F.scaled_dot_product_attention(xq, xk, xv, attn_mask=attn_mask, dropout_p=dropout_p, is_causal=True) # 高性能实现,自动加上因果 mask output = softmax(QK^T/sqrt(d)+mask)V->droupout (bsz,self.n_local_heads,seq_len,self,head_dim)
else:
scores = (xq @ xk.transpose(-2, -1)) / math.sqrt(self.head_dim) # Q @ K^T / sqrt(d_k),形状:(bsz, self.n_local_heads, seq_len, seq_len)
scores = scores + torch.triu(
torch.full((seq_len, seq_len), float("-inf"), device=scores.device),
diagonal=1
).unsqueeze(0).unsqueeze(0) # scores+mask (bsz,self.n_local_heads,seq_len,seq_len)
if attention_mask is not None:
extended_attention_mask = attention_mask.unsqueeze(1).unsqueeze(2) # (bsz, seq_len)->(bsz, 1, 1, seq_len)
extended_attention_mask = (1.0 - extended_attention_mask) * -1e9 #
scores = scores + extended_attention_mask # (bsz,self.n_local_heads,seq_len,seq_len)
scores = F.softmax(scores.float(), dim=-1).type_as(xq) # (bsz,self.n_local_heads,seq_len,seq_len)
scores = self.attn_dropout(scores)
output = scores @ xv # (bsz,self.n_local_heads,seq_len,seq_len)*(bsz,self.n_local_heads,seq_len,self.head_dim)
# output = (bsz,self.n_local_heads,seq_len,self.head_dim)
output = output.transpose(1, 2).reshape(bsz, seq_len, -1) # (bsz, seq_len,self.n_local_heads*self.head_dim)
output = self.resid_dropout(self.o_proj(output))
return output, past_kv
# 最终输出形状;# (bsz, seq_len,self.n_local_heads*self.head_dim)
# = (bsz, seq_len, hidden_size)FFN部分(采用了GLU结构)
前置知识1:函数ACT2FN
python
self.act_fn = ACT2FN[config.hidden_act]-
ACT2FN是个字典,存了激活函数名字到实现的映射,比如:pythonACT2FN = { "relu": torch.nn.functional.relu, "gelu": torch.nn.functional.gelu, "silu": torch.nn.functional.silu, # SiLU = Swish } -
在 LLaMA 系列里,激活函数是 SiLU (又叫 Swish)。
数学形式:
\[\text{SiLU}(x) = x \cdot \sigma(x) = \frac{x}{1 + e^{-x}} \]
前置知识2:GLU风格的FFN结构
这个 FFN 用的是 Gated Linear Unit (GLU) 风格:
\[\text{FFN}(x) = W_{down} \Big( \text{SiLU}(W_{gate} x) \odot (W_{up} x) \Big) \]
其中:
- \(W_{gate}, W_{up} \in \mathbb{R}^{d_{hidden} \times d_{inter}}\)
- \(W_{down} \in \mathbb{R}^{d_{inter} \times d_{hidden}}\)
- \(\odot\) 表示逐元素乘法。
python
# 输入形状: (bsz, seq_len, hidden_size)
# 中间有门控节
# 输出形状: (bsz, seq_len, hidden_size)
class FeedForward(nn.Module):
def __init__(self, config: MiniMindConfig):
super().__init__()
if config.intermediate_size is None:
intermediate_size = int(config.hidden_size * 8 / 3) # 通常设为hidden_size的8/3倍
config.intermediate_size = 64 * ((intermediate_size + 64 - 1) // 64) # 对齐到 64 的整数倍,硬件友好
self.gate_proj = nn.Linear(config.hidden_size, config.intermediate_size, bias=False)
self.down_proj = nn.Linear(config.intermediate_size, config.hidden_size, bias=False)
self.up_proj = nn.Linear(config.hidden_size, config.intermediate_size, bias=False)
self.dropout = nn.Dropout(config.dropout)
self.act_fn = ACT2FN[config.hidden_act]
def forward(self, x):
return self.dropout(self.down_proj(self.act_fn(self.gate_proj(x)) * self.up_proj(x)))MOE 模块 (混合专家模型)
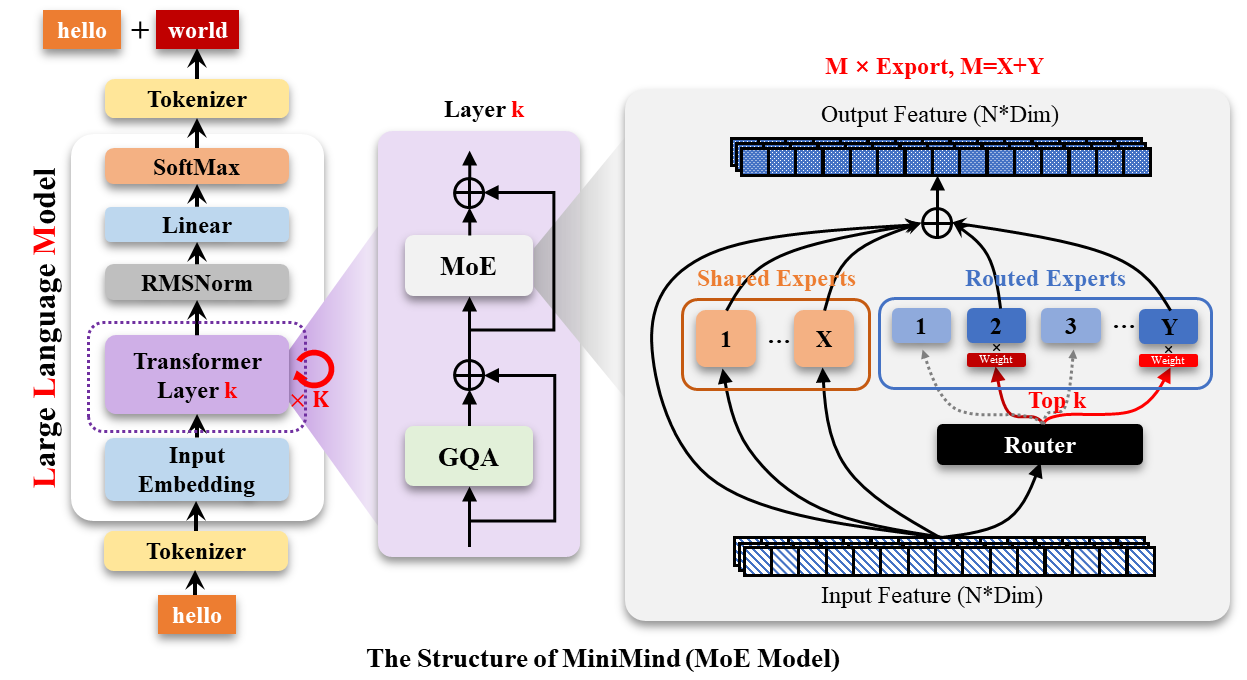
整体结构
详细的可参见苏剑林博客:https://spaces.ac.cn/archives/10699 我觉得写的很好,我自己如何整理也不如这篇博客讲的清晰了。
简答来说,在MInimind的模型里,MOE模块是这样的
- 1 有一部分共享专家,总是被选择
- 2 有一个打分器(Router),其数学形式为\(\underbrace{[\rho_1,\rho_2,\cdots,\rho_n]}{\rho}=h(\boldsymbol{xW}^{(R)})\quad\in\mathbb{R}{\geq0}^n\)
- 3 选择top-k个专家,并对其打分进行softmax归一化,加权求和
- 4 计算负载均衡loss,鼓励路由器均匀使用专家
前置torch知识
torch.Tensor.scatter_add_(dim, index, src):在指定的维度dim上,按照index里的位置,把src中的值「加到」当前 Tensor 的对应位置上。
index: 索引 Tensor,和src形状相同,表示要加到目标 Tensor 的哪个位置。src: 源 Tensor,包含要加的值。
python
import torch
# 初始 Tensor
out = torch.zeros(3, 5, dtype=torch.float)
# 索引
index = torch.tensor([[0, 1, 2],
[2, 3, 4]])
# 源值
src = torch.tensor([[1, 1, 1],
[2, 2, 2]], dtype=torch.float)
out.scatter_add_(1, index, src)
print(out)结果输出;
python
tensor([[1., 1., 1., 0., 0.],
[0., 0., 2., 2., 2.],
[0., 0., 0., 0., 0.]])dim=1 表示在第 1 个维度(列递增方向)上 scatter。第一行的 1 分别加到了第 0、1、2 列。第二行的 2 分别加到了第 2、3、4 列。
torch.nn.functional.one_hot(tensor, num_classes):将整数 Tensor 转换为 one-hot 编码形式。
tensor: 输入的整数 Tensor,元素值应在[0, num_classes-1]范围内。num_classes: 类别总数,决定 one-hot 向量的长度。
python
import torch
# 输入的整数 Tensor
tensor = torch.tensor([0, 2, 1, 3])
# 转换为 one-hot 编码
one_hot = torch.nn.functional.one_hot(tensor, num_classes=4)
"""
tensor([[1, 0, 0, 0],
[0, 0, 1, 0],
[0, 1, 0, 0],
[0, 0, 0, 1]])
"""MOE Gate
python
# 输入形状: (bsz, seq_len, hidden_size)
# 输出: topk_idx (bsz*seq_len, top_k), topk_weight (bsz*seq_len, top_k), aux_loss (可求导的标量)
class MoEGate(nn.Module):
def __init__(self, config: MiniMindConfig):
super().__init__()
self.top_k = config.num_experts_per_tok # 每个 token 选择多少个专家
self.n_routed_experts = config.n_routed_experts # 总共多少个专家
self.scoring_func = config.scoring_func # 打分方式(一般是 softmax)
self.alpha = config.aux_loss_alpha # 辅助损失的权重
self.seq_aux = config.seq_aux # 是否用序列级别的辅助损失
self.norm_topk_prob = config.norm_topk_prob # 是否对 top-k 概率归一化
self.gating_dim = config.hidden_size
# Router 的核心参数,相当于 [n_experts, hidden_dim] 的打分矩阵
self.weight = nn.Parameter(torch.empty((self.n_routed_experts, self.gating_dim)))
self.reset_parameters()forward部分:首先输出每个 token 在专家上的分布,形状为(bsz*seq_len, n_experts) (token数量,可投票选择的专家数量),然后选出topk及其索引,根据接收参数决定是都要归一化
python
def forward(self, hidden_states):
bsz, seq_len, h = hidden_states.shape
hidden_states = hidden_states.view(-1, h) # [batch * seq, hidden_dim]
# 计算 gating logits: [batch*seq, n_experts]
logits = F.linear(hidden_states, self.weight, None)
# softmax 得到每个 token 在专家上的分布
scores = logits.softmax(dim=-1)
# 选出前 top-k 个专家
# topk_weight: [batch*seq, top_k], topk_idx: [batch*seq, top_k]
topk_weight, topk_idx = torch.topk(scores, k=self.top_k, dim=-1, sorted=False)
# 如果需要,归一化 top-k 权重,让它们和为 1
if self.top_k > 1 and self.norm_topk_prob:
denominator = topk_weight.sum(dim=-1, keepdim=True) + 1e-20
topk_weight = topk_weight / denominator紧接着计算aux_loss,促进负载平衡.关于aux_loss的计算,有序列级别(句子级别)和token级别两种计算方式。先看序列级别的aux_loss:
python
# 负载均衡辅助损失 (aux_loss),避免所有 token 都路由到同一个专家
if self.training and self.alpha > 0.0: # 只在训练时计算 aux_loss,判断alpha是否大于0是因为如果alpha=0则不需要计算aux_loss
scores_for_aux = scores # (bsz*seq_len, n_experts)
aux_topk = self.top_k # 每个 token 选择的专家数
# 将 topk_idx 转换为二维形状,方便后续计算
topk_idx_for_aux_loss = topk_idx.view(bsz, -1) # (bsz, seq_len*top_k) 每一行是一个bsz的所有句子token选择的专家索引,排列在一起共计seq_len*k个
if self.seq_aux: # 是否使用序列级别的辅助损失
scores_for_seq_aux = scores_for_aux.view(bsz, seq_len, -1) # (B,seq_len,n_experts)
ce = torch.zeros(bsz, self.n_routed_experts, device=hidden_states.device) # (bsz, n_experts) 一个bsz等于一个句子,ce用于累计每个句子中各专家的使用频率
# 统计方式:每一个bsz内累加专家使用次数,然后除以归一化常数
ce.scatter_add_(
1, topk_idx_for_aux_loss,
torch.ones(bsz, seq_len * aux_topk, device=hidden_states.device)
).div_(seq_len * aux_topk / self.n_routed_experts)
# 计算scores_for_seq_aux.mean(dim=1) (B,seq_len,n_experts)-> (B,n_experts) 每个bsz内各专家获得的平均打分
# ce (bsz, n_experts) 每个bsz内各专家的实际使用频率
aux_loss = (ce * scores_for_seq_aux.mean(dim=1)).sum(dim=1).mean() * self.alpha从代码来看,aux_loss的含义比较清晰,就是打分(归一化概率分布)和实际使用频率的乘积之和。这一项存在约束:分数之和是固定的,而实际使用频率和打分的分布大致是正相关的。在这样的约束下,我们感性上便可以发现(类似于基本不等式),如果专家使用的不均衡,那么这一项auxloss应该会更大一些。反之,如果专家使用均衡,那么这一项auxloss会更小一些。因此,最小化auxloss的目标,实际上是鼓励专家使用均衡。更详细的、严格的解释可见:https://spaces.ac.cn/archives/10735
aux_loss的另一种计算方式是token级别的aux_loss(原理类似):
python
else:
# token 级别:类似 one-hot,鼓励负载均衡
# (bsz, seq_len*top_k) -> (bsz*seq_len*top_k, n_experts)
mask_ce = F.one_hot(topk_idx_for_aux_loss.view(-1), num_classes=self.n_routed_experts)
ce = mask_ce.float().mean(0) # 每个专家的实际使用比例
Pi = scores_for_aux.mean(0) # 理论分布
fi = ce * self.n_routed_experts # 归一化因子
aux_loss = (Pi * fi).sum() * self.alpha
else:
aux_loss = 0最后,返回topk的索引、权重和aux_loss
python
return topk_idx, topk_weight, aux_lossMOE的FFN
先看一般的前馈
python
class MOEFeedForward(nn.Module):
def __init__(self, config: MiniMindConfig):
super().__init__()
self.config = config
self.experts = nn.ModuleList([
FeedForward(config)
for _ in range(config.n_routed_experts)
])
self.gate = MoEGate(config)
if config.n_shared_experts > 0:
self.shared_experts = nn.ModuleList([
FeedForward(config)
for _ in range(config.n_shared_experts)
])
# 输入 形状: (bsz, seq_len, hidden_size)
# 输出 形状: (bsz, seq_len, hidden_size)
def forward(self, x):
identity = x
orig_shape = x.shape
bsz, seq_len, _ = x.shape
# 使用门控机制选择专家
topk_idx, topk_weight, aux_loss = self.gate(x) # topk_idx: (bsz*seq_len, top_k), topk_weight: (bsz*seq_len, top_k)
x = x.view(-1, x.shape[-1]) # (bsz*seq_len, hidden_size)
flat_topk_idx = topk_idx.view(-1) # (bsz*seq_len*top_k, ) # 所有句子所有token的topk id选择排列为一行
if self.training:
x = x.repeat_interleave(self.config.num_experts_per_tok, dim=0) # (bsz*seq_len*top_k, hidden_size)
y = torch.empty_like(x, dtype=torch.float16) # (bsz*seq_len*top_k, hidden_size)
for i, expert in enumerate(self.experts): # 遍历所有专家
y[flat_topk_idx == i] = expert(x[flat_topk_idx == i]).to(y.dtype) # 所有使用了专家i的token都送进去expert i计算,赋值到y对应位置
# 按照 topk_weight 加权求和
# (bsz*seq_len,top_k, hidden_size)
y = (y.view(*topk_weight.shape, -1) * topk_weight.unsqueeze(-1)).sum(dim=1) # (bsz*seq_len,top_k, hidden_size)* (bsz*seq_len,top_k,1) sum-> (bsz*seq_len, hidden_size)
y = y.view(*orig_shape) # (bsz, seq_len, hidden_size)
else: # 推理时
y = self.moe_infer(x, flat_topk_idx, topk_weight.view(-1, 1)).view(*orig_shape)
if self.config.n_shared_experts > 0:
for expert in self.shared_experts:
y = y + expert(identity)
self.aux_loss = aux_loss
return y推理时的MOE计算:
python
@torch.no_grad()
def moe_infer(self, x, flat_expert_indices, flat_expert_weights):
expert_cache = torch.zeros_like(x)
idxs = flat_expert_indices.argsort()
tokens_per_expert = flat_expert_indices.bincount().cpu().numpy().cumsum(0)
token_idxs = idxs // self.config.num_experts_per_tok
# 当tokens_per_expert = [6, 15, 20, 26],tokens_per_expert.shape[0]即为专家数量(此时为4)
# 且token_idxs = [3, 7, 19, 21, 24, 25, 4, 5, 6, 10, 11, 12...] 时
# 意味token_idxs[:6] -> [3, 7, 19, 21, 24, 25]这6个位置属于专家0处理的token(每个token有可能被多个专家处理,这取决于num_experts_per_tok)
# 接下来9个位置token_idxs[6:15] -> [4, 5, 6, 10, 11, 12...]属于专家1处理的token...依此类推
for i, end_idx in enumerate(tokens_per_expert):
start_idx = 0 if i == 0 else tokens_per_expert[i - 1]
if start_idx == end_idx:
continue
expert = self.experts[i]
exp_token_idx = token_idxs[start_idx:end_idx]
expert_tokens = x[exp_token_idx]
expert_out = expert(expert_tokens).to(expert_cache.dtype)
expert_out.mul_(flat_expert_weights[idxs[start_idx:end_idx]])
expert_cache.scatter_add_(0, exp_token_idx.view(-1, 1).repeat(1, x.shape[-1]), expert_out)
return expert_cache完全的架构
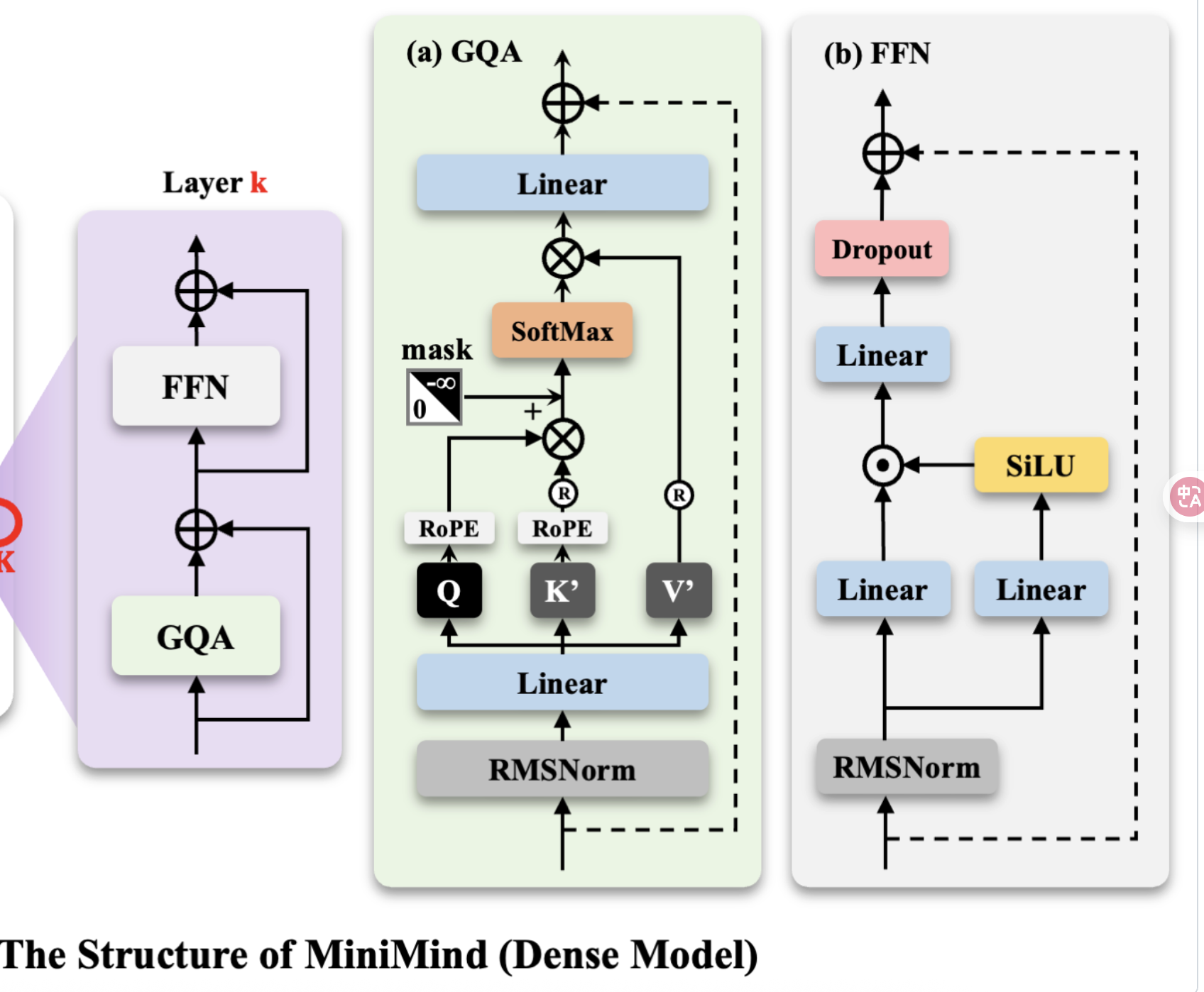
单个Minimind block = GQA + FFN/ MOE
| MOE | FFN |
|---|---|
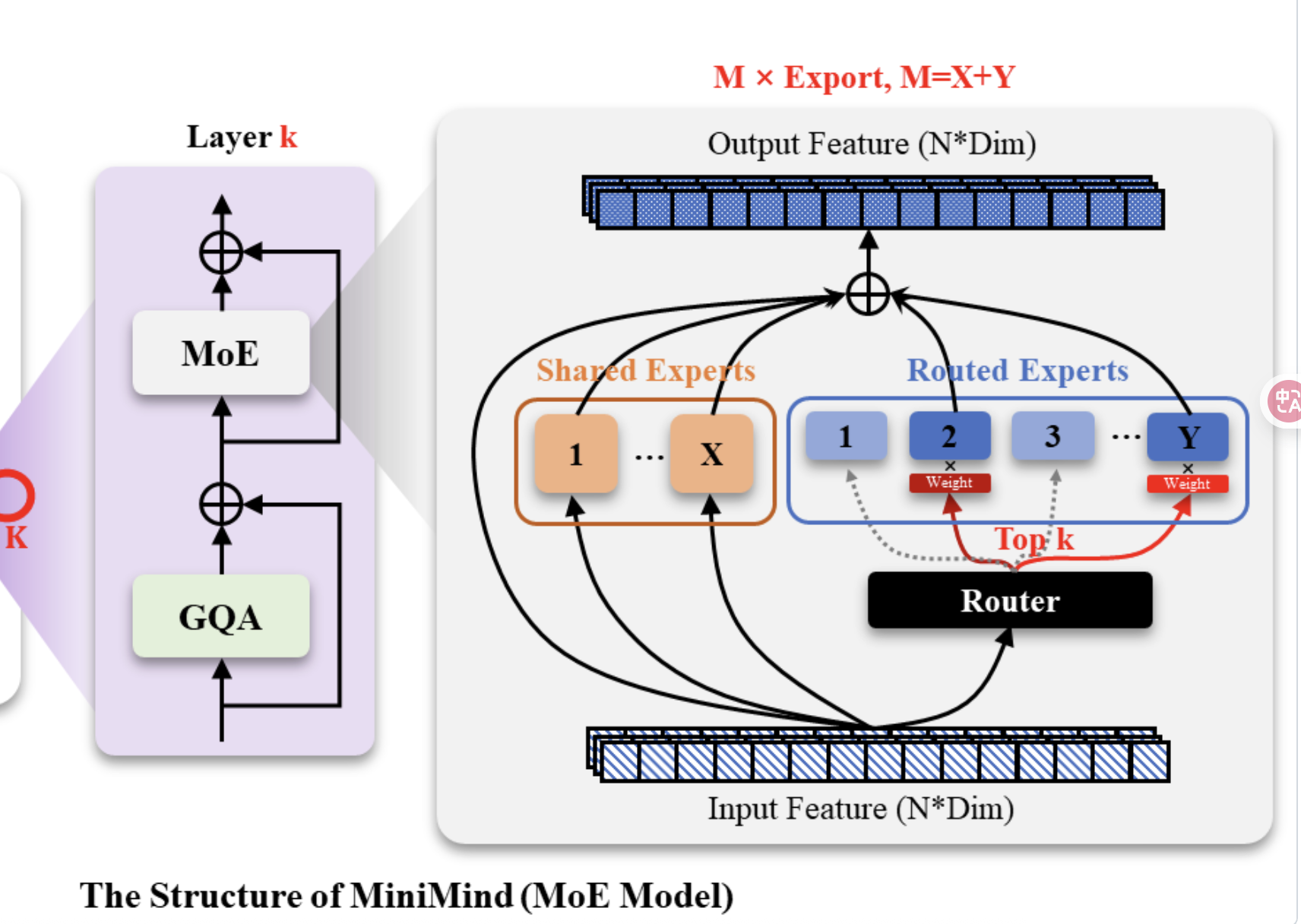 |
 |
python
class MiniMindBlock(nn.Module):
def __init__(self, layer_id: int, config: MiniMindConfig):
super().__init__()
# 注意力头的数量
self.num_attention_heads = config.num_attention_heads
# 隐层维度大小
self.hidden_size = config.hidden_size
# 每个注意力头的维度 = hidden_size / num_heads
self.head_dim = config.hidden_size // config.num_attention_heads
# 自注意力层(包含 QKV 计算、多头注意力、输出映射等)
self.self_attn = Attention(config)
# 层的编号(主要用于模型内部调试或分布式并行时定位)
self.layer_id = layer_id
# 输入到 Attention 前的 RMSNorm(Pre-LN 结构)
self.input_layernorm = RMSNorm(config.hidden_size, eps=config.rms_norm_eps)
# 输入到 FFN/MoE 前的 RMSNorm(第二个 Pre-LN)
self.post_attention_layernorm = RMSNorm(config.hidden_size, eps=config.rms_norm_eps)
# 前馈网络:可以是普通 FFN,也可以是 MoE 版本
self.mlp = FeedForward(config) if not config.use_moe else MOEFeedForward(config)
def forward(
self,
hidden_states, # 输入序列 (B, L, d),B=batch,L=序列长度,d=隐层维度
position_embeddings, # 位置编码,用于注意力计算
past_key_value=None, # KV cache(推理时加速用)
use_cache=False, # 是否启用 KV 缓存
attention_mask=None # 注意力 mask(避免看未来或 padding 部分)
):
# === 1. Self-Attention 子层 ===
residual = hidden_states # 保存残差
hidden_states, present_key_value = self.self_attn(
self.input_layernorm(hidden_states), # LN -> Attention
position_embeddings,
past_key_value,
use_cache,
attention_mask
)
hidden_states += residual # 残差连接: H = H + Attention(LN(H))
# === 2. FFN/MoE 子层 ===
residual = hidden_states # 再次保存残差
hidden_states = hidden_states + self.mlp(
self.post_attention_layernorm(hidden_states) # LN -> MLP
)
# 输出处理后的序列表示 + KV cache
return hidden_states, present_key_value整体Bone
1. self.embed_tokens = nn.Embedding(config.vocab_size, config.hidden_size)
- 作用 :这是一个 可训练的查表层(lookup table),常用于词向量(token embedding)。
- 输入 :一个
LongTensor,形状(batch_size, seq_len),里面是 token 的 整数索引 (范围[0, vocab_size-1])。 - 输出 :一个
FloatTensor,形状(batch_size, seq_len, hidden_size),即每个 token 被映射为一个hidden_size维的向量。 - 训练性 :参数(embedding 矩阵大小为
(vocab_size, hidden_size))是 可学习的 ,会在训练时更新。
除非你加载了某个预训练好的 embedding 矩阵,否则默认是随机初始化。
比如:
python
import torch
import torch.nn as nn
embed = nn.Embedding(1000, 64) # 1000个token,维度64
x = torch.tensor([[1, 5, 8], [2, 9, 3]]) # batch=2, seq_len=3
out = embed(x) # (2, 3, 64)2. register_buffer 的作用
python
self.register_buffer("freqs_cos", freqs_cos, persistent=False)
self.register_buffer("freqs_sin", freqs_sin, persistent=False)-
作用 :把
freqs_cos和freqs_sin注册为 buffer。 -
区别于参数:
- 参数 (
nn.Parameter):会被优化器更新(训练时变化)。 - buffer :不会训练更新,但会随着
model.state_dict()保存/加载。
- 参数 (
-
是不是全局变量?
不是全局变量,而是模型内部的持久状态 。你可以通过
self.freqs_cos访问,但它不在 Python 全局命名空间里,只属于模型对象。 -
能不能随处访问?
可以在模型的方法里随意用,但要通过模型实例访问,比如:
pythonmodel.freqs_cos # ✅ freqs_cos # ❌(除非单独定义)
所以 register_buffer 的本质是:模型的常量状态,存着就行,不要训练更新。
3. forward 最终输出
-
输出:
pythonhidden_states # shape = (batch_size, seq_len, hidden_size) -
这相当于是 transformer encoder/decoder 最后一层的 上下文表示,还没有做 softmax。
python
class MiniMindModel(nn.Module):
def __init__(self, config: MiniMindConfig):
super().__init__()
self.config = config
# 模型的词表大小和层数
self.vocab_size, self.num_hidden_layers = config.vocab_size, config.num_hidden_layers
# 词嵌入层 (token embedding),把输入的 token id 映射到 hidden_size 维的向量
self.embed_tokens = nn.Embedding(config.vocab_size, config.hidden_size)
# dropout 用于防止过拟合
self.dropout = nn.Dropout(config.dropout)
# 堆叠多个 Transformer Block,每层是 MiniMindBlock
self.layers = nn.ModuleList([MiniMindBlock(l, config) for l in range(self.num_hidden_layers)])
# 最后的归一化层,使用 RMSNorm(比 LayerNorm 更高效)
self.norm = RMSNorm(config.hidden_size, eps=config.rms_norm_eps)
# 预计算旋转位置编码 RoPE 所需的 cos 和 sin 值
freqs_cos, freqs_sin = precompute_freqs_cis(
dim=config.hidden_size // config.num_attention_heads, # 每个注意力头的维度
end=config.max_position_embeddings, # 最大支持的序列长度
theta=config.rope_theta # RoPE 的缩放参数
)
# 注册为 buffer,表示这些不是参数(不会参与训练),但会随着模型保存/加载
self.register_buffer("freqs_cos", freqs_cos, persistent=False)
self.register_buffer("freqs_sin", freqs_sin, persistent=False)
def forward(self,
input_ids: Optional[torch.Tensor] = None, # 输入 token 序列 [batch_size, seq_length]
attention_mask: Optional[torch.Tensor] = None, # 注意力掩码
past_key_values: Optional[List[Tuple[torch.Tensor, torch.Tensor]]] = None, # KV 缓存
use_cache: bool = False, # 是否启用 KV 缓存(加速推理)
**kwargs):
# 获取 batch_size 和序列长度
batch_size, seq_length = input_ids.shape
# 如果没有传递 KV 缓存,初始化为 None
past_key_values = past_key_values or [None] * len(self.layers)
# 如果有缓存,确定从哪个位置开始(start_pos)
start_pos = past_key_values[0][0].shape[1] if past_key_values[0] is not None else 0
# 将 token id 转换为向量,并做 dropout
hidden_states = self.dropout(self.embed_tokens(input_ids))
# 取出对应序列长度的 RoPE 位置编码 (cos, sin)
position_embeddings = (
self.freqs_cos[start_pos:start_pos + seq_length],
self.freqs_sin[start_pos:start_pos + seq_length]
)
# 保存每一层的 KV,用于下次增量推理
presents = []
# 遍历每一层 Transformer Block
for layer_idx, (layer, past_key_value) in enumerate(zip(self.layers, past_key_values)):
hidden_states, present = layer(
hidden_states, # 当前层输入
position_embeddings, # RoPE 编码
past_key_value=past_key_value,
use_cache=use_cache,
attention_mask=attention_mask
)
presents.append(present) # 保存当前层的 KV
# 最后一层 RMSNorm
hidden_states = self.norm(hidden_states)
# 如果是 MoE 层,需要计算 auxiliary loss(负载均衡损失)
aux_loss = sum(
layer.mlp.aux_loss
for layer in self.layers
if isinstance(layer.mlp, MOEFeedForward)
)
# 输出:最后的 hidden states( shape = (batch_size, seq_len, hidden_size))、每层 KV 缓存、MoE 的辅助损失
return hidden_states, presents, aux_lossHead(下游任务和因果语言建模)
上文,我们得到了最终的hidden_states,形状为(batch_size, seq_len, hidden_size)。但我们知道,大语言模型的本质是把下一个token的预测问题转化为一个类别数量=词表大小的多分类问题,这需要我们把hidden_states通过softmax转换为词表大小的维度上输出概率。因此,最后的代码实际上起到了这样的作用。
python
class MiniMindForCausalLM(PreTrainedModel, GenerationMixin):
# -------------------------------
# 1. HuggingFace 的规范要求
# -------------------------------
# PreTrainedModel 是 HuggingFace 的基类,负责参数保存/加载、权重初始化等。
# GenerationMixin 提供了 generate() 方法的实现(自回归解码用)。
# config_class 是 HuggingFace 约定的字段,告诉框架用什么配置类来构建模型。
config_class = MiniMindConfig
def __init__(self, config: MiniMindConfig = None):
# --------------------------------
# 2. 初始化配置
# --------------------------------
# 如果没有传入配置,就使用默认的 MiniMindConfig。
self.config = config or MiniMindConfig()
# 必须调用父类的 __init__ 来注册 config(PreTrainedModel 需要它)。
super().__init__(self.config)
# --------------------------------
# 3. 模型主体
# --------------------------------
# 主体是 MiniMindModel (相当于 Transformer Encoder/Decoder 堆叠)
self.model = MiniMindModel(self.config)
# 语言建模头(LM Head)
# 线性层: (hidden_size -> vocab_size)
# 输入: (bsz, seq_len, hidden_size)
# 输出: (bsz, seq_len, vocab_size)
self.lm_head = nn.Linear(
self.config.hidden_size, self.config.vocab_size, bias=False
)
# 权重 tying (权重共享):
# 将 embedding 层和输出层共享参数,以减少参数量并提升泛化。
# 两者形状都是 (vocab_size, hidden_size)。
self.model.embed_tokens.weight = self.lm_head.weight
# HuggingFace 约定的输出容器(dict-like),存储 logits/hidden_states 等。
self.OUT = CausalLMOutputWithPast()
def forward(self,
input_ids: Optional[torch.Tensor] = None, # (bsz, seq_len),输入 token 序列
attention_mask: Optional[torch.Tensor] = None, # (bsz, seq_len),mask 用于避免 padding 干扰
past_key_values: Optional[List[Tuple[torch.Tensor, torch.Tensor]]] = None,
# past_key_values 用于缓存 kv,推理时减少重复计算
use_cache: bool = False, # 是否启用缓存(加速生成)
logits_to_keep: Union[int, torch.Tensor] = 0,
**args):
# -------------------------------
# 4. 主干模型前向
# -------------------------------
# h: (bsz, seq_len, hidden_size) -> 隐藏状态
# past_kvs: List[...] -> 缓存的 KV,用于加速生成
# aux_loss: 可能存在的额外损失(如 MoE 专家均衡损失)
h, past_kvs, aux_loss = self.model(
input_ids=input_ids,
attention_mask=attention_mask,
past_key_values=past_key_values,
use_cache=use_cache,
**args
)
# -------------------------------
# 5. logits 截取
# -------------------------------
# logits_to_keep 用于控制返回哪些时间步的预测结果:
# - 若为 int,如 1,表示只保留最后 1 个 token 的预测结果(常见于推理)。
# - 若为 0,默认保留全部。
# - 若为张量,可自定义索引。
slice_indices = slice(-logits_to_keep, None) if isinstance(logits_to_keep, int) else logits_to_keep
# 计算输出 logits
# h[:, slice_indices, :] : (bsz, slice_len, hidden_size)
# lm_head -> (bsz, slice_len, vocab_size)
logits = self.lm_head(h[:, slice_indices, :])
# -------------------------------
# 6. 按 HuggingFace 规范组织输出
# -------------------------------
# 存储最后隐藏状态 (训练时可能需要)
self.OUT.__setitem__('last_hidden_state', h) # (bsz, seq_len, hidden_size)
# 存储 logits (训练/推理都需要)
self.OUT.__setitem__('logits', logits) # (bsz, slice_len, vocab_size)
# 存储额外损失(如 MoE 负载均衡损失)
self.OUT.__setitem__('aux_loss', aux_loss) # (标量)
# 存储 past_kvs,推理时用于缓存
self.OUT.__setitem__('past_key_values', past_kvs)
return self.OUT重要参考文献
- 原始开源项目:https://github.com/jingyaogong/minimind
- https://zhuanlan.zhihu.com/p/28786272137 介绍了transfomer中使用的全部mask,从目的到具体形式,图文并茂,写的很清晰,感谢作者给出这样优质的博客!
- https://spaces.ac.cn/archives/10699 苏剑林大佬的MOE环游记系列,清晰地介绍了MOE的提出动机,提高效率的原理,以及aux_loss的设计
- Rope(Su. et al.):https://spaces.ac.cn/archives/8265
- 有关transfomer的基础教程,网络上很多了,不再一一赘婿。