一文看懂指数函数：基础与性质

指数函数是数学中常见的一类函数，形式通常为 <math xmlns="http://www.w3.org/1998/Math/MathML"> f ( x ) = a x f(x) = a^x </math>f(x)=ax，其中底数 <math xmlns="http://www.w3.org/1998/Math/MathML"> a a </math>a 是常数 <math xmlns="http://www.w3.org/1998/Math/MathML"> （ a > 0 且 a ≠ 1 ）（a>0且 a≠1） </math>（a>0且a=1），自变量 <math xmlns="http://www.w3.org/1998/Math/MathML"> x x </math>x 是指数。以下是关于指数函数的详细说明，适合初学者理解：

1. 基本形式

标准形式： <math xmlns="http://www.w3.org/1998/Math/MathML"> y = a x y = a^x </math>y=ax
- <math xmlns="http://www.w3.org/1998/Math/MathML"> a a </math>a 称为底数（base），是正实数且不等于 1（因为 <math xmlns="http://www.w3.org/1998/Math/MathML"> a = 1 a=1 </math>a=1 时函数退化为常数函数 <math xmlns="http://www.w3.org/1998/Math/MathML"> y = 1 y=1 </math>y=1）。
- <math xmlns="http://www.w3.org/1998/Math/MathML"> x x </math>x 是指数（exponent），可以是任意实数。
常见特例：自然指数函数 <math xmlns="http://www.w3.org/1998/Math/MathML"> y = e x y = e^x </math>y=ex，其中 <math xmlns="http://www.w3.org/1998/Math/MathML"> e ≈ 2.71828 e≈2.71828 </math>e≈2.71828（自然常数）。

2. 定义域和值域

定义域 ：所有实数（ <math xmlns="http://www.w3.org/1998/Math/MathML"> x ∈ R x∈R </math>x∈R），因为任何实数指数都有定义（例如 <math xmlns="http://www.w3.org/1998/Math/MathML"> a − 2 = 1 a 2 ， a 0.5 = a a^{-2} = \frac{1}{a^2}，a^{0.5} = \sqrt{a} </math>a−2=a21，a0.5=a ）。
值域：正实数（ <math xmlns="http://www.w3.org/1998/Math/MathML"> y > 0 y>0 </math>y>0），即函数值始终为正。

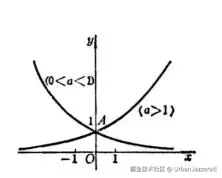
3. 图像特征

当 <math xmlns="http://www.w3.org/1998/Math/MathML"> a > 1 a>1 </math>a>1时：
- 函数单调递增（即 <math xmlns="http://www.w3.org/1998/Math/MathML"> x x </math>x 增大， <math xmlns="http://www.w3.org/1998/Math/MathML"> y y </math>y 增大）。
- 图像过点 <math xmlns="http://www.w3.org/1998/Math/MathML"> ( 0 , 1 ) (0,1) </math>(0,1)（因为 <math xmlns="http://www.w3.org/1998/Math/MathML"> a 0 = 1 a^0 = 1 </math>a0=1）。
- 随着 <math xmlns="http://www.w3.org/1998/Math/MathML"> x → − ∞ ， y → 0 x→−∞，y→0 </math>x→−∞，y→0（趋近于 x 轴但不接触）；随着 <math xmlns="http://www.w3.org/1998/Math/MathML"> x → + ∞ ， y → + ∞ 。 x→+∞，y→+∞。 </math>x→+∞，y→+∞。
当 <math xmlns="http://www.w3.org/1998/Math/MathML"> 0 < a < 1 0<a<1 </math>0<a<1 时：
- 函数单调递减。
- 同样过点 <math xmlns="http://www.w3.org/1998/Math/MathML"> ( 0 , 1 ) (0,1) </math>(0,1)。
- <math xmlns="http://www.w3.org/1998/Math/MathML"> 随着 x → − ∞ ， y → + ∞ ；随着 x → + ∞ ， y → 0 。随着 x→−∞，y→+∞；随着 x→+∞，y→0。 </math>随着x→−∞，y→+∞；随着x→+∞，y→0。

4. 重要性质

指数法则（运算法则）：
1. <math xmlns="http://www.w3.org/1998/Math/MathML"> a m ⋅ a n = a m + n a^m \cdot a^n = a^{m+n} </math>am⋅an=am+n
2. <math xmlns="http://www.w3.org/1998/Math/MathML"> a m a n = a m − n \frac{a^m}{a^n} = a^{m-n} </math>anam=am−n
3. <math xmlns="http://www.w3.org/1998/Math/MathML"> ( a m ) n = a m ⋅ n (a^m)^n = a^{m \cdot n} </math>(am)n=am⋅n
4. <math xmlns="http://www.w3.org/1998/Math/MathML"> a − n = 1 a n a^{-n} = \frac{1}{a^n} </math>a−n=an1
5. <math xmlns="http://www.w3.org/1998/Math/MathML"> a 1 / n = a n a^{1/n} = \sqrt[n]{a} </math>a1/n=na

5. 实际应用

复利计算：本金 <math xmlns="http://www.w3.org/1998/Math/MathML"> P P </math>P 以年利率 <math xmlns="http://www.w3.org/1998/Math/MathML"> r r </math>r 连续复利， <math xmlns="http://www.w3.org/1998/Math/MathML"> t t </math>t 年后总额为 $A = P e^{rt}v。

6. 常见误区

指数函数 <math xmlns="http://www.w3.org/1998/Math/MathML"> a x a^x </math>ax 与幂函数 <math xmlns="http://www.w3.org/1998/Math/MathML"> x a x^a </math>xa不同：前者指数是变量，底数是常数；后者底数是变量，指数是常数。
注意底数 <math xmlns="http://www.w3.org/1998/Math/MathML"> a a </math>a 必须为正（负底数可能导致无定义，如 <math xmlns="http://www.w3.org/1998/Math/MathML"> ( − 2 ) 0.5 (-2)^{0.5} </math>(−2)0.5 不是实数）。

7. 简单例子

<math xmlns="http://www.w3.org/1998/Math/MathML"> f ( x ) = 2 x ： f(x) = 2^x： </math>f(x)=2x：
- <math xmlns="http://www.w3.org/1998/Math/MathML"> f ( 0 ) = 1 , f ( 1 ) = 2 , f ( 2 ) = 4 , f ( − 1 ) = 0.5 f(0)=1, f(1)=2, f(2)=4, f(−1)=0.5 </math>f(0)=1,f(1)=2,f(2)=4,f(−1)=0.5
<math xmlns="http://www.w3.org/1998/Math/MathML"> g ( x ) = ( 1 2 ) x ： g(x) = \left(\frac{1}{2}\right)^x： </math>g(x)=(21)x：
- <math xmlns="http://www.w3.org/1998/Math/MathML"> g ( 0 ) = 1 , g ( 1 ) = 0.5 , g ( 2 ) = 0.25 g(0)=1, g(1)=0.5, g(2)=0.25 </math>g(0)=1,g(1)=0.5,g(2)=0.25