此分类用于记录吴恩达深度学习课程的学习笔记。
课程相关信息链接如下:
- 原课程视频链接:[双语字幕]吴恩达深度学习deeplearning.ai
- github课程资料,含课件与笔记:吴恩达深度学习教学资料
- 课程配套练习(中英)与答案:吴恩达深度学习课后习题与答案
本篇为第一课第二周,是2.3,2.9和2.10部分的笔记内容。
可能会发现跳过了几节,实际上是因为课程中的顺序为讲解结构后再分别讲解基础的顺序,笔记为了便于理解,便改为先讲解基础后可以顺畅的理解结构的顺序。跳过的节数在之前已讲到,或在之后再讲到。
本周的课程以逻辑回归为例详细介绍了神经网络的运行,传播等过程,其中涉及大量机器学习的基础知识和部分数学原理,如没有一定的相关基础,理解会较为困难。
因为,笔记并不直接复述视频原理,而是从基础开始,尽可能地创造一个较为丝滑的理解过程。
首先,经过之前的第三部分内容学习,我们了解了梯度下降法,本篇延续逻辑,进行传播部分的讲解。
现在我们知道了如何寻找结果最优的权重 \(w\) 和偏置 \(b\) ,我们已经具备了大部分基础,最后来系统的梳理一下具体传播过程。
我们以此开始本篇笔记的内容。
1.损失函数和成本函数
1.1 损失函数是什么?
损失函数(Loss Function)是机器学习和优化中的一个重要概念,它衡量的是模型预测值与实际值之间的差距。通常,损失函数的目标是最小化预测误差,从而使模型能够更好地拟合数据。
具体来说,损失函数将模型预测值与真实值之间的误差量化为一个数字,通常这个数字越小,表示模型的预测越准确。不同的任务(如回归、分类等)会使用不同类型的损失函数。
现在,假设我们有 \(m\) 个样本来训练模型,就像之前提到的规范一样:
我们将第一个样本表示为\((x^{(1)},y^{(1)})\) 第二个为 \((x^{(2)},y^{(2)})\) 依此类推。
这里的 \(y\) 是确定的标签,也就是我们之前说的 "答案"。
而我们将模型输出的预测值表示为:\(\hat{y}\) ,而我们的目的就是让\(\hat{y}\) 和 \(y\) 的差距最小,来实现更好的拟合。
1.2 如何定义损失函数?
这里我们先了解在机器学习里定义的一类函数的概念:凸函数
一个函数 \(f(x)\) 被称为凸函数,则如果对于定义域中的任意两个点 \(x_1\) 和 \(x_2\),以及任意的 \(\lambda \in [0, 1]\),都有:
\[f(\lambda x_1 + (1 - \lambda) x_2) \leq \lambda f(x_1) + (1 - \lambda) f(x_2) \]
看起来有些复杂了,我们并不细推公式,而是用例子来理解一下这个概念:
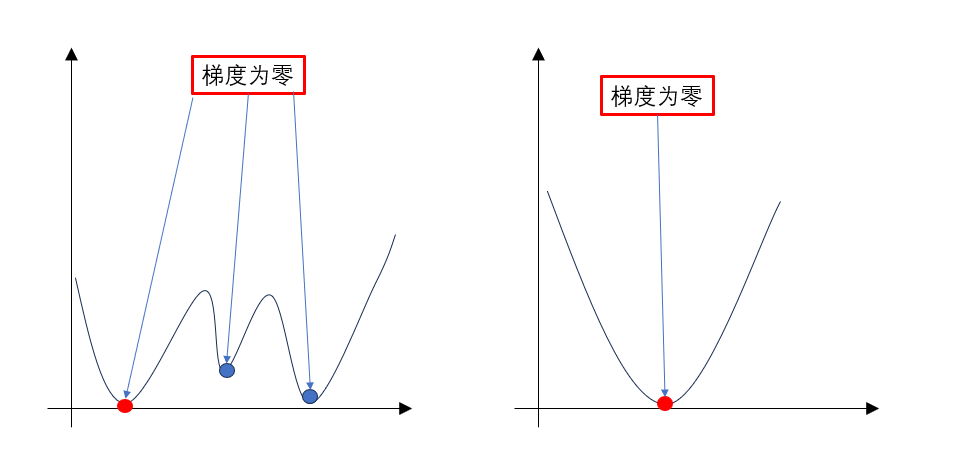
我们来看图中的两幅函数图像(梯度应为三维以上使用,这里画为二维方便理解 ),并探讨梯度下降法在这两幅图像的应用。
这里先补充一点:当梯度等于0时,就代表这是一个"平稳点",但要判断其是局部最大/最小/水平区域,还需要二阶导数,此处了解即可。
观察左侧图像,我们可以通过看到得知红色的点是该函数的全局最小值,而于此同时,该函数还存在两个局部最小值。
根据梯度的概念,我们会发现,如果在这样一个函数里应用梯度下降法来寻找最小值,这三个点是没有区别的,也就是说:在这样的函数里,梯度下降法可能会误把局部最小值当成全局最小值 。
我们就把这样的函数称作非凸函数。
而右侧的函数就不会出现这样的问题,如果一个函数是凸的,那么它的局部最小值就是全局最小值。这使得优化问题更加容易解决,因为在凸优化中,不存在局部最小值和全局最小值的差异。
因此,简单总结凸函数:凸函数具有"弯曲向上"的形状,且其局部最小值即为全局最小值。
如果一个函数不是凸的,那么它可能有多个局部最小值,而不是唯一的全局最小值。优化这类函数时,可能会遇到困境,比如陷入局部最小值而无法找到全局最小值。在机器学习中,非凸函数的优化更加复杂。
因此,我们更希望用凸函数来作为损失函数 。
当然,也有例外,但在深度学习中,由于模型复杂性(例如神经网络),即使损失函数本身是凸的,整体的损失函数仍然可能变得非凸,我们遇到再说。
1.3 逻辑回归的损失函数是什么?
对于分类问题 ,我们常使用是损失函数叫交叉熵损失 (Binary Cross-Entropy Loss),衡量的是实际类别与预测概率分布之间的差异。
我们先来看二分类交叉熵损失函数的公式,对于单个样本,其定义为:
\[L(\hat{y},y) = -[y \log(\hat{y}) + (1 - y ) \log(1 - \hat{y})] \]
其中:
- \(L\) 是交叉熵损失
- \(y\)是真实标签,取值为 0 或 1
- \(\hat{y}\) 是预测值,表示样本属于类 1 的概率(通过 sigmoid 函数计算)
我们把标签代入,用结果来理解这个公式,交叉熵公式的形式本身也是综合了凸函数的考量。
- 当 \(y\) 等于1时,公式变为:$$L(\hat{y},y) = -\log(\hat{y})$$
这时,我们希望结果最小,就是希望\(-\log(\hat{y})\) 尽可能小,也就是让\(\hat{y}\) 尽可能大。而 \(\hat{y}\) 是通过sigmoid函数得到的一个介于0和1之间的数,要让\(\hat{y}\) 尽可能大,是不是就要向1靠拢,也就是向正确标签靠拢? - 当 \(y\) 等于0时,公式变为:$$L(\hat{y},y) = -\log(1 - \hat{y})$$
同理,希望\(\log(1 - \hat{y})\) 尽可能小,就要让\(\hat{y}\) 向0靠拢。
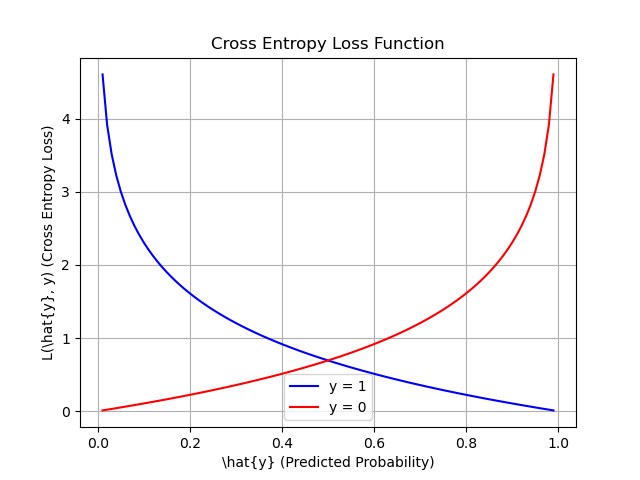
这样就初步解释了为什么要用这种形式的函数作为损失函数,这样,在我们应用梯度下降进行最小化时,预测值便会不断向正确标签靠拢,\(w和b\) 也会不断优化。
1.4 逻辑回归的成本函数是什么?
通过刚刚的损失函数,我们已经知道对于单个样本如何得到一个预测和标签量化的差别,那再扩展到 \(m\) 个样本,即衡量全部样本的训练效果的函数,就是成本函数,也叫代价函数。
逻辑回归的成本函数公式如下:
\[J(w,b) = \frac{1}{m} \sum_{i=1}^{m} L(y,\hat{y})=- \frac{1}{m} \sum_{i=1}^{m} \left[ y^{(i)} \log(\hat{y}) + (1 - y^{(i)}) \log(1 - \hat{y}) \right] \]
实际上,就是所有样本的损失函数的平均值 ,我们根据这个数来进行下一步优化。
要补充的一点是,在现在的实际使用中,我们通常不会说单个样本的损失函数,而是用损失函数的名字直接代替成本函数,这里我们根据吴恩达老师的课程内容进行更系统化的介绍。
1.5 如何根据成本函数优化参数?
现在我们已经知道了如何得到预测和标签的差值,又知道了可以通过梯度下降法最小化差值优化参数,现在我们来看一下这个具体过程如何实现。
假设我们现在有两个输入特征,即
\[\hat{y}=w_1x_1+w_2x_2+b \]
再根据梯度的计算方法,我们可以得到:
\[\nabla J(w_1,w_2,b) = ( \frac{\partial J(w_1,w_2,b) }{\partial w_1}, \frac{\partial J(w_1,w_2,b) }{\partial w_2} ,\frac{\partial J(w_1,w_2,b) }{\partial b}) \]
现在我们得到了代价函数的梯度,要怎么具体应用梯度下降法呢?
我们再引入一个概念:学习率
在深度学习中,学习率 (Learning Rate)是指在优化过程中,每次更新模型参数时步长的大小,其符号表示为\(\eta\)
学习率我们可以手工设置为一个固定值,也有一些相关算法,但学习率过大可能会导致跨度过高错过最优解,而学习率过小可能会导致收敛速度过慢,甚至陷入局部最优解。
在经历一轮训练后,我们便得到了一个梯度,而根据这个梯度,我们这样更新参数:
\[w_1=w_1-\eta\frac{\partial J(w_1,w_2,b) }{\partial w_1} \]
通过这个式子,我们便可以理解,学习率其实就是梯度下降的步长。
其他变量也是同理,而经过一轮训练,模型就会再计算一次梯度,再一次下降,直到找到最优解。
2.传播
其实在这两篇的叙述中,我们已经把逻辑回归的正向传播和反向传播都过了一遍,现在我们来系统的梳理一下传播过程。
2.1正向传播
先看概念:
在深度学习中,正向传播(Forward Propagation)是指输入数据通过神经网络逐层传递并计算输出的过程。它是模型做出预测的核心步骤,也是后续计算损失和进行反向传播的前提。
以逻辑回归为例,逻辑回归的正向传播就是输入经过线性回归,sigmoid激活函数,计算得到输出的过程。
2.2 反向传播
还是先看概念:
反向传播(Backpropagation) 是训练神经网络时用于优化模型的一种重要算法。它的目的是通过计算梯度并更新网络的权重和偏置,从而最小化损失函数。反向传播是基于链式法则的,核心思想是:通过计算每一层的梯度信息,从输出层"反向"传递到输入层,逐层更新网络参数。
同样以逻辑回归为例,逻辑回归的反向传播就是通过输出计算代价函数,计算梯度,再根据梯度下降法更新参数的过程。
这里要注意一下概念里提到的链式法则 ,这适用于神经网络中的多层隐藏层间的梯度计算和更新,而加入反向传播的逻辑回归实际上相当于只有一个隐藏神经元的神经网络,于是就没有在这里展开介绍链式法则,我们会在不久后构建神经网络时再详细展开链式法则,在有实例的情况下去理解。
2.3 传播图
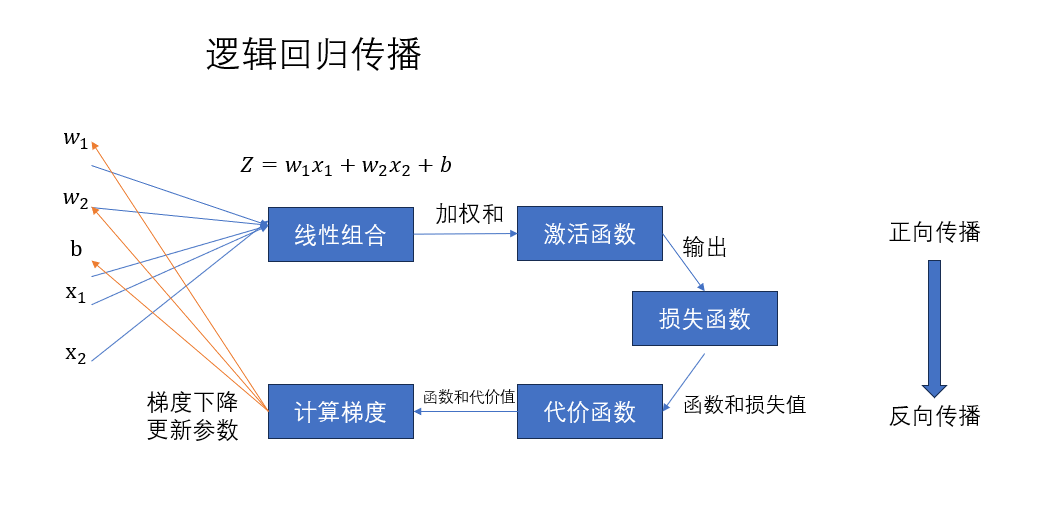
如图所示,经过一轮传播,参数就会得到一次更新,也就完成了一次优化。这其中的任何一个环节,都已经出现在本篇和之前的博客里。
经过一轮轮传播,我们遍一次次训练 \(w和b\) 最终实现拟合效果。
这就是逻辑回归的传播过程。