GELU (Gaussian Error Linear Unit) 激活函数详解
1. 概述
GELU,全称为"高斯误差线性单元",是一种高性能的、平滑的激活函数。与 ReLU 及其变体(如 Leaky ReLU, ELU)相比,GELU 引入了随机正则化的思想,通过一个概率性的方式来决定神经元的输出,并在众多任务上被证实优于前者。
2. 核心思想
ReLU 的工作方式可以被看作一个"硬门控 (hard gate)":当输入 <math xmlns="http://www.w3.org/1998/Math/MathML"> x > 0 x > 0 </math>x>0 时,门是开的(输出 <math xmlns="http://www.w3.org/1998/Math/MathML"> x x </math>x);当 <math xmlns="http://www.w3.org/1998/Math/MathML"> x ≤ 0 x \le 0 </math>x≤0 时,门是关的(输出 <math xmlns="http://www.w3.org/1998/Math/MathML"> 0 0 </math>0)。
GELU 的核心思想则更为精妙,它采用了一个**"随机门控 (stochastic gate)"**。一个神经元的输出值 <math xmlns="http://www.w3.org/1998/Math/MathML"> x x </math>x 将乘以一个在 [0, 1] 之间的值,这个值是随机生成的,但其概率分布取决于输入 <math xmlns="http://www.w3.org/1998/Math/MathML"> x x </math>x 本身。
具体来说,GELU 使用标准正态分布的累积分布函数 (CDF) ,用 <math xmlns="http://www.w3.org/1998/Math/MathML"> Φ ( x ) \Phi(x) </math>Φ(x) 表示,来作为这个门控的概率值。
- 如果输入 <math xmlns="http://www.w3.org/1998/Math/MathML"> x x </math>x 越大, <math xmlns="http://www.w3.org/1998/Math/MathML"> Φ ( x ) \Phi(x) </math>Φ(x) 就越接近 1,意味着这个输入有很大概率被"保留"。
- 如果输入 <math xmlns="http://www.w3.org/1998/Math/MathML"> x x </math>x 越小(越负), <math xmlns="http://www.w3.org/1998/Math/MathML"> Φ ( x ) \Phi(x) </math>Φ(x) 就越接近 0,意味着这个输入有很大概率被"置零"。
这种方式将神经元的激活与它的数值分布联系起来,实现了一种数据驱动的、非线性的门控机制。
3. 数学公式
精确公式
GELU 的数学定义非常简洁:
<math xmlns="http://www.w3.org/1998/Math/MathML"> GELU ( x ) = x ⋅ Φ ( x ) \text{GELU}(x) = x \cdot \Phi(x) </math>GELU(x)=x⋅Φ(x)
其中 Φ(x) 是标准正态分布 N(0,1) 的累积分布函数 (CDF),即:
<math xmlns="http://www.w3.org/1998/Math/MathML"> Φ ( x ) = P ( X ≤ x ) = 1 2 π ∫ − ∞ x e − t 2 / 2 d t \Phi(x) = P(X \le x) = \frac{1}{\sqrt{2\pi}} \int_{-\infty}^{x} e^{-t^2/2} dt </math>Φ(x)=P(X≤x)=2π 1∫−∞xe−t2/2dt
近似计算公式
由于标准正态分布的 CDF 没有解析解,计算起来比较耗时。因此,在实践中,通常使用一个快速且精确的近似公式。最著名的一个是利用 tanh 函数进行近似:
<math xmlns="http://www.w3.org/1998/Math/MathML"> GELU ( x ) ≈ 0.5 x ( 1 + tanh [ 2 π ( x + 0.044715 x 3 ) ] ) \text{GELU}(x) \approx 0.5x \left( 1 + \tanh\left[\sqrt{\frac{2}{\pi}} \left( x + 0.044715 x^3 \right)\right] \right) </math>GELU(x)≈0.5x(1+tanh[π2 (x+0.044715x3)])
这个近似公式在 PyTorch 和 TensorFlow 等主流框架中被广泛采用。
4. 关键特性与优势
-
平滑性 (Smoothness)
GELU 的函数曲线处处平滑可导,相比于 ReLU 在 x=0 处的突变点("尖角"),GELU 的平滑特性更有利于梯度的计算和模型的优化。
-
非单调性 (Non-Monotonic)
观察 GELU 的函数图像可以发现,在负数区域它有一个轻微的"凹陷",即它不是一个单调递增函数。这种非单调性可能增加了函数捕获数据中更复杂模式的能力。
-
随机正则化的直观解释
GELU 的门控机制可以被看作是一种隐性的、数据驱动的 Dropout。与 Dropout 以固定概率随机丢弃神经元不同,GELU 丢弃神经元的概率取决于神经元自身的激活值,这可以被认为是一种更智能的正则化方法。
-
优越的性能
大量实验表明,在 Transformer 等基于注意力的模型中,使用 GELU 作为前馈网络(Feed-Forward Network)的激活函数,相比 ReLU 及其变体,能够带来更快的收敛速度和更高的模型性能。
5. GELU vs. ReLU (视觉对比)
-
ReLU : 在 <math xmlns="http://www.w3.org/1998/Math/MathML"> x ≤ 0 x \le 0 </math>x≤0 时为一条直线 <math xmlns="http://www.w3.org/1998/Math/MathML"> y = 0 y=0 </math>y=0。在 <math xmlns="http://www.w3.org/1998/Math/MathML"> x > 0 x > 0 </math>x>0 时为一条直线 <math xmlns="http://www.w3.org/1998/Math/MathML"> y = x y=x </math>y=x。在原点有一个尖锐的拐点。
-
GELU:
- 当 <math xmlns="http://www.w3.org/1998/Math/MathML"> x x </math>x 很大时,函数曲线非常接近 <math xmlns="http://www.w3.org/1998/Math/MathML"> y = x y=x </math>y=x。
- 当 <math xmlns="http://www.w3.org/1998/Math/MathML"> x x </math>x 是很大的负数时,函数曲线非常接近 <math xmlns="http://www.w3.org/1998/Math/MathML"> y = 0 y=0 </math>y=0。
- 在原点附近平滑过渡,并且在负值区域会略低于 x 轴。
先放pytorch实现的结果图
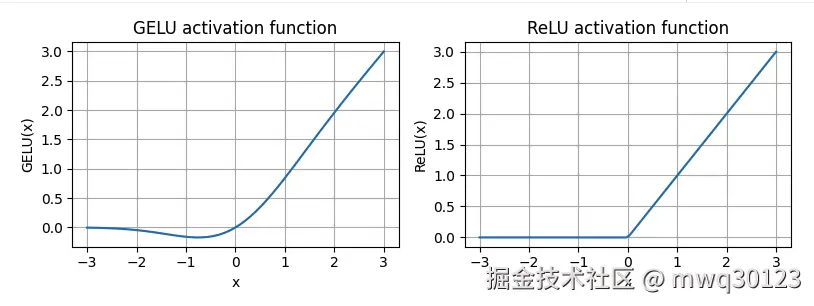
6. PyTorch 实现
在 PyTorch 中使用 GELU 非常简单,它已经被内置为标准模块。
python
import torch
import torch.nn as nn
# 这里,我们自定义一个
class GELU(nn.Module):
def __init__(self):
super().__init__()
def forward(self, x):
return 0.5 * x * (1 + torch.tanh(
#这一步把它变得平滑了很多
torch.sqrt(torch.tensor(2.0 / torch.pi)) * (x + 0.044715 * torch.pow(x, 3))
))
import matplotlib.pyplot as plt
gelu, relu = GELU(), nn.ReLU()#先把函数给个小名
# Some sample data
x = torch.linspace(-3, 3, 100) #初定义一个张量
y_gelu, y_relu = gelu(x), relu(x) #两种激活函数
plt.figure(figsize=(8, 3))
for i, (y, label) in enumerate(zip([y_gelu, y_relu], ["GELU", "ReLU"]), 1):
plt.subplot(1, 2, i)
plt.plot(x, y)
plt.title(f"{label} activation function")
plt.xlabel("x")
plt.ylabel(f"{label}(x)")
plt.grid(True)
plt.tight_layout()
plt.show()
#一个经典的作图