本文系东哥原创文章,100天风控节选内容,不支持任何转载,抄袭和侵权必究。
大家好,我是东哥。
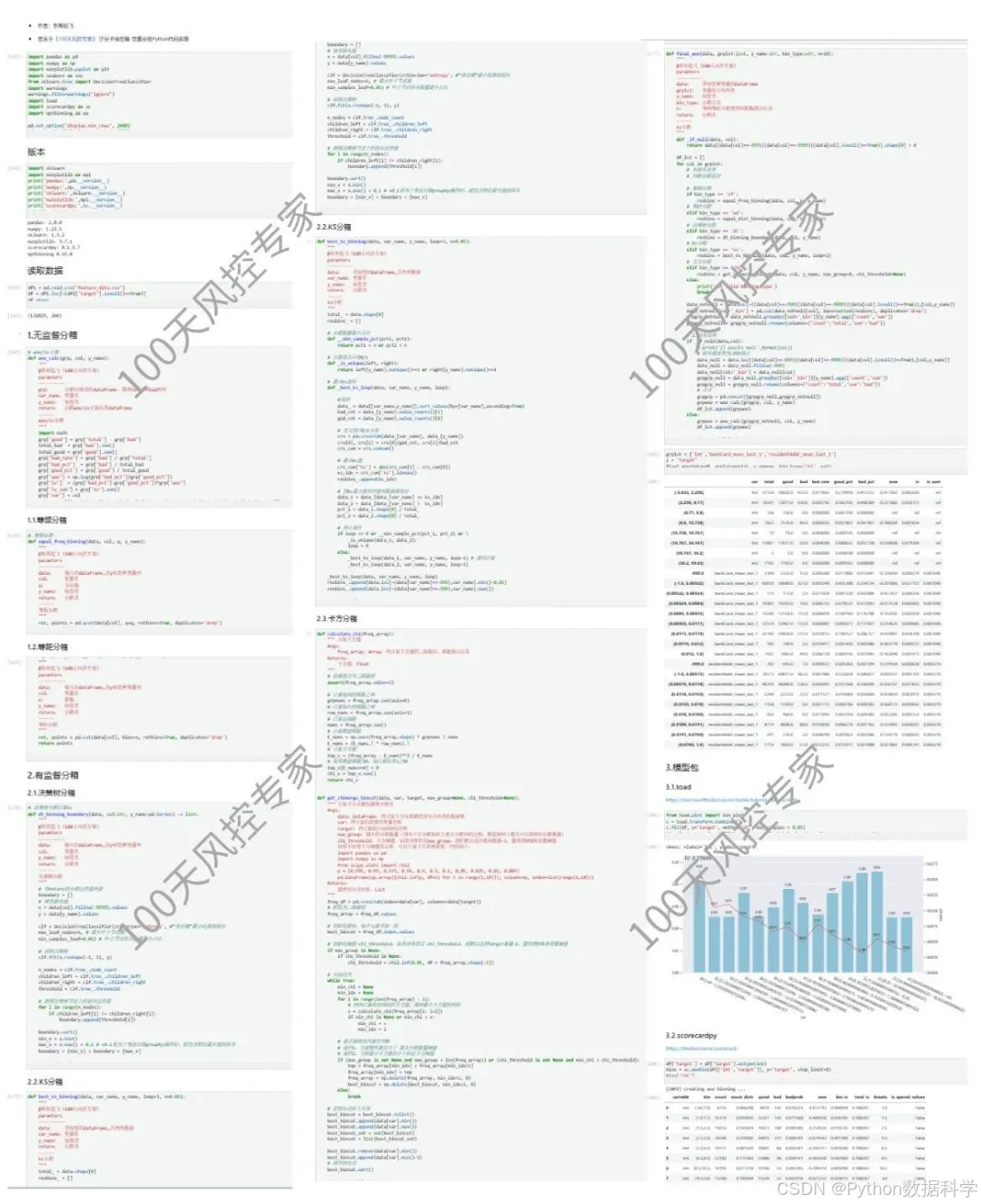
信贷风控领域中,无论做策略规则还是模型,经常需要对变量进行分箱操作。而分箱的算法比较繁杂,本次就分享下常用的几种分箱算法,以及Python的代码实操,内容节选自👉《100天风控专家》。
首先直接亮出分箱算法的分类导图,然后分别介绍各个分箱算法。
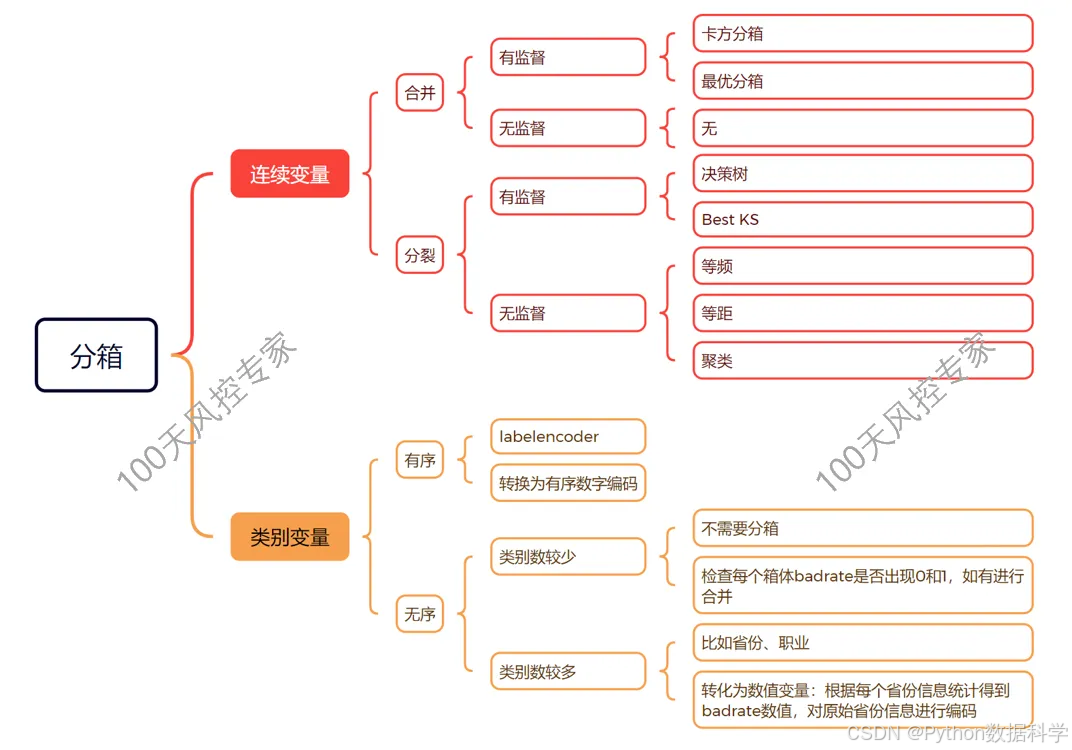
1. 等频等距分箱
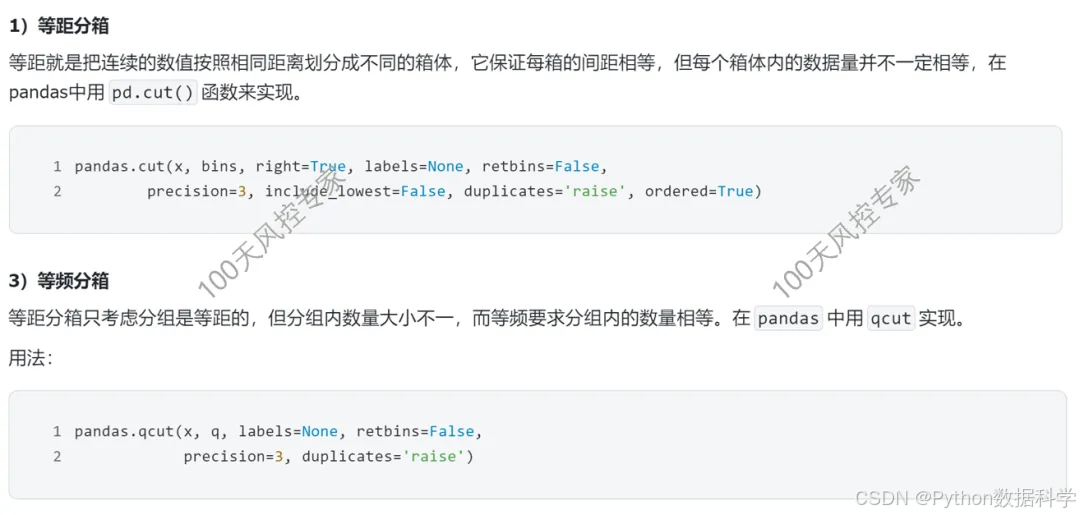
等频/等距分箱是最简单基础的分箱方式,定义如下:
- 等频分箱:将整体样本量切成N等分,即每箱的样本数量相同。
- 等距分箱:将变量按照固定的长度距离分箱,即每箱的区间范围大小相同。
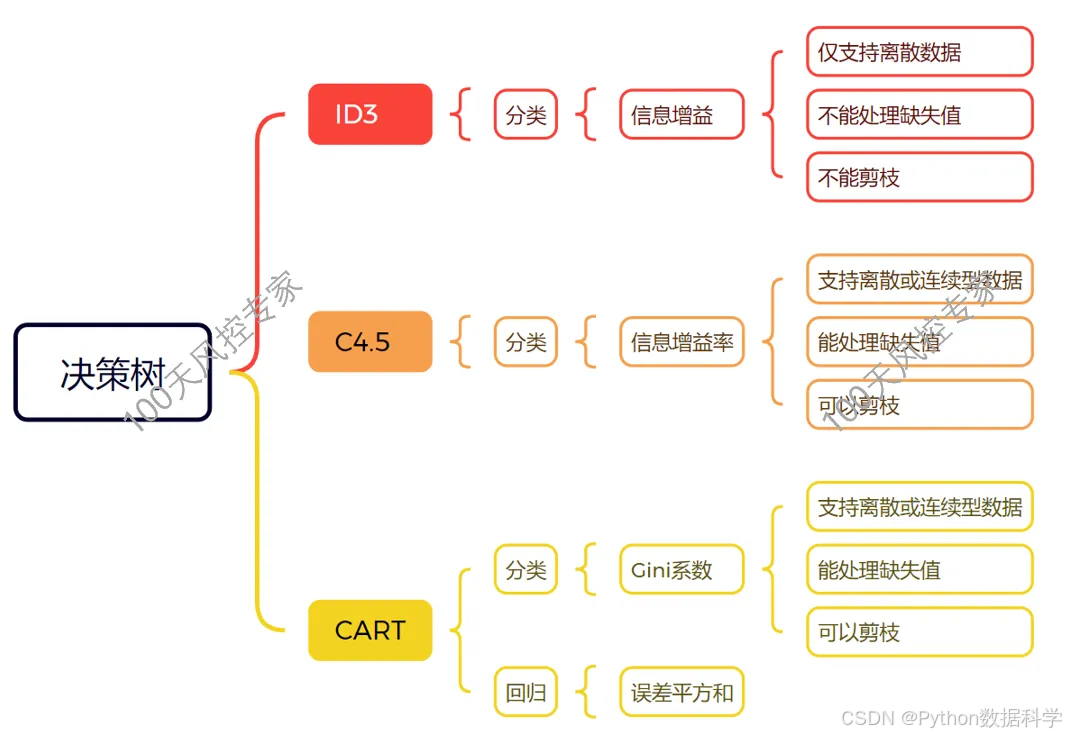
2. 决策树分箱
决策树有常见以下三种算法:ID3、C4.5、CART,其中CART作为集中树的算法基础,是更为常用的,所以主要讲解CART算法。
1)CART(分类回归树)
CART是"Classification and Regression
Trees" 的缩写,意思是 "分类回归树 "。从它的名字上就不难理解了,CART算法是既可以用于分类的,也可以用于回归的。CART分类树算法使用"基尼系数(Gini)"选择特征,基尼系数代表了模型的不纯度,基尼系数越小,不纯度越低,特征越好。公式如下:
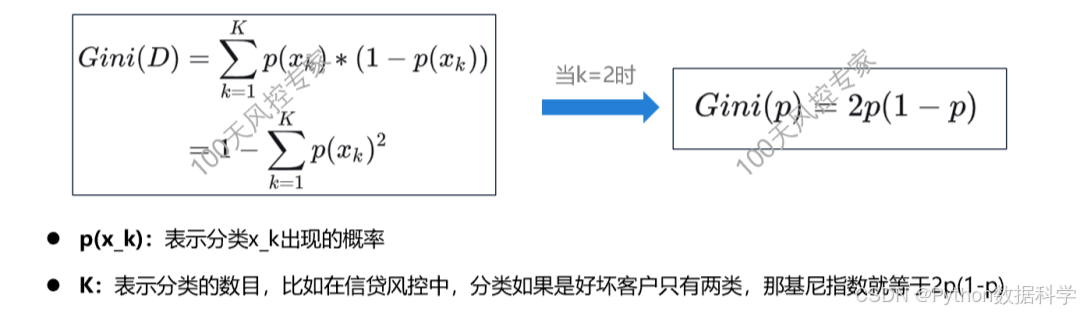
2)二分类的Gini系数
对于给定的样本集合D,其基尼指数定义为:

- k:代表类别
- C_k:代表D中属于第k类的样本子集
当CART 为二分类时,则在特征A的条件下,集合D的基尼指数定义为:
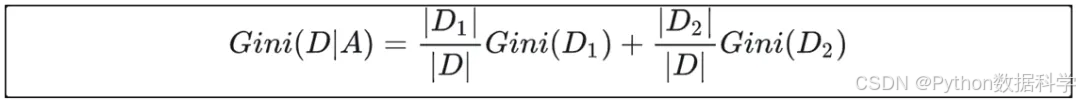
3)连续变量的基尼系数计算过程
对于连续型变量,假如变量a有连续值m个,从小到大排列。m个数值就有m-1个切分点,分别使用每个切分点把连续数值离散划分成两类,将分裂前数据集D按照划分点分为D1和D2两个子集,然后计算每个划分点下对应的基尼指数,选择值最小的一个作为最终的变量划分。
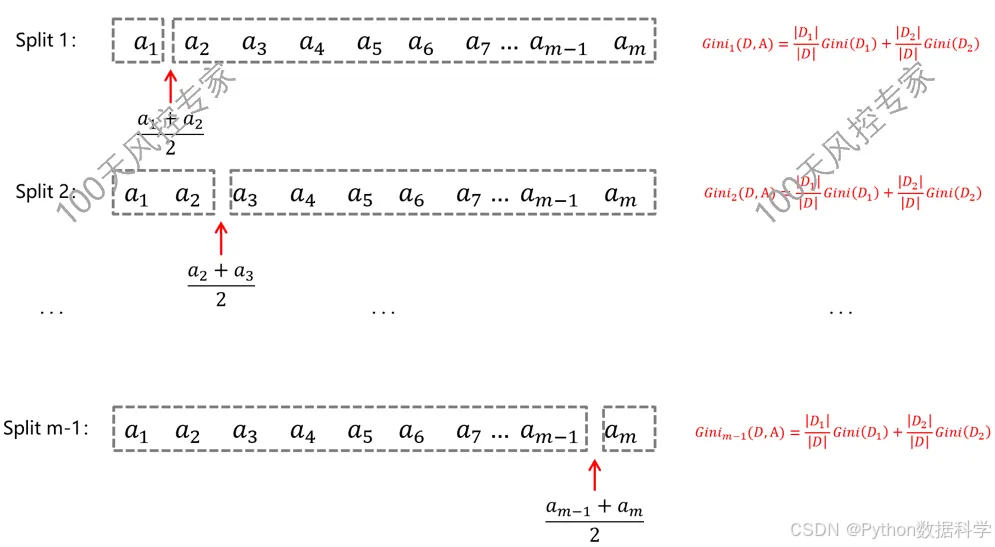
4)CART树用于分箱
通常CART用于构造一个模型或者寻找规则组合,此时有多个变量参与其中,每个分裂点所使用的变量根据基尼系数大小可能不同。而将CART应用在变量分箱时,变量只有一个,即每个分裂节点都只有同一变量,但由于分裂后的样本是分裂前的子集,使基尼系数最大的分裂点也会发生变化。
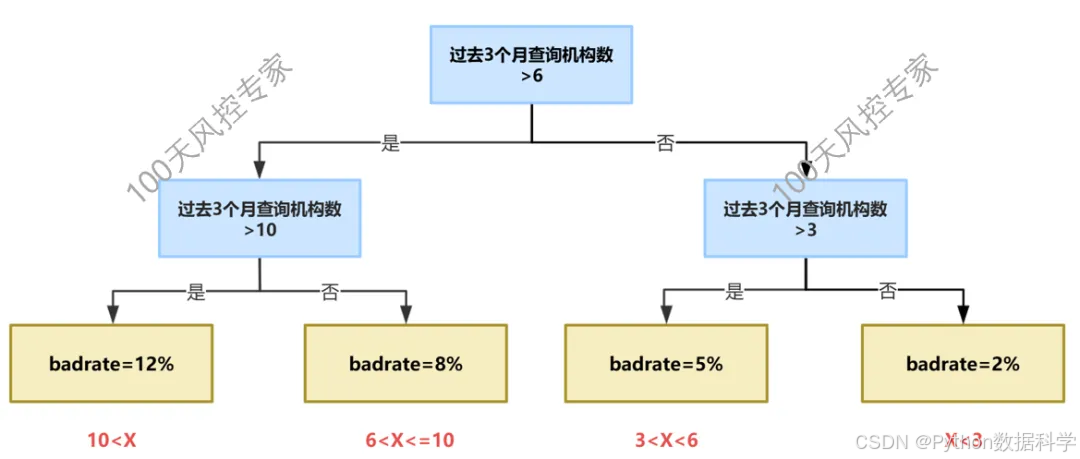
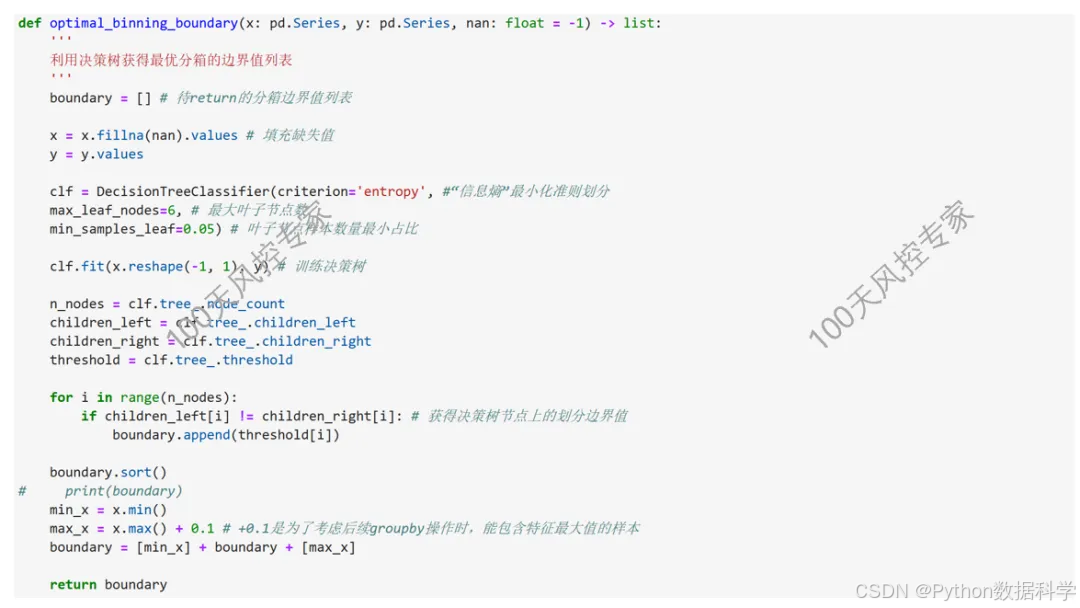
完整介绍和代码参考👉《100天风控专家》
3. KS分箱
1)原理
通过KS指标可以求得让好坏客户分布差异最大化的分箱点,而BestKS分箱方法就是基于KS指标实现的。
2)计算步骤
以连续型变量X为例,其具体做法是:
①先対变量值进行排序
②计算每个变量值对应的KS
③选取KS最大所对应的变量值XT,然后以XT将当前样本划分为两部分(X<=XT)和 (X>XT)
④对于每个样本循环重复步骤2-3,直到触发了停止条件的任何一条
3)停止条件
停止条件就是让以上步骤不再继续分箱的条件,一般可以包括:
①划分以后每个分箱的样本量占比小于一定的阈值,比如5%
②划分以后每个分箱对应的y标签全部为好客户或者坏客户

完整介绍和代码参考👉《100天风控专家》
4. 卡方分箱
1)卡法原理
卡方分箱是一种基于"卡方检验"的分箱方法,通过独立性检验来实现核心分箱功能。背后的基本思想是:如果两个相邻的区间具有非常类似的类分布,那么这两个区间可以合并。否则,它们应该分开。低卡方值表明它们具有相似的类分布。卡方分箱算法简单来说,有两个部分组成:
①初始化步骤
根据连续变量值大小进行排序
构建最初的离散化,即把每一个单独的值视为一个箱体。这样做的目的就是想从每个单独的个体开始逐渐合并。
②合并(自底向上的合并,直到满足停止条件)
计算所有相邻分箱的卡方值:也就是说如果有1,2,3,4个分箱,那么就需要绑定相邻的两个分箱,共三组:12,23,34。然后分别计算三个绑定组的卡方值。
从计算的卡方值中找出最小的一个,并把这两个分箱合并:比如,23是卡方值最小的一个,那么就将2和3合并,本轮计算中分箱就变为了1,23,4。
2)停止条件
①卡方停止的阈值
②分箱数目的限制
只要当所有分箱对的卡方值都大于阈值,并且分箱数目小于最大分箱数时,计算就会继续,直到不满足。这两个值根据我们的经验来定义,作为函数参数设置,一般推荐使用0.9,0.95,0.99的置信度,分箱数一般可以设置为5。

卡方分箱论文链接:https://sci2s.ugr.es/keel/pdf/algorithm/congreso/1992-Kerber-ChimErge-AAAI92.pdf
4)卡方分箱示例
举个例子说明一下这个公式是如何用的,对于相邻两个分箱的卡方值计算:
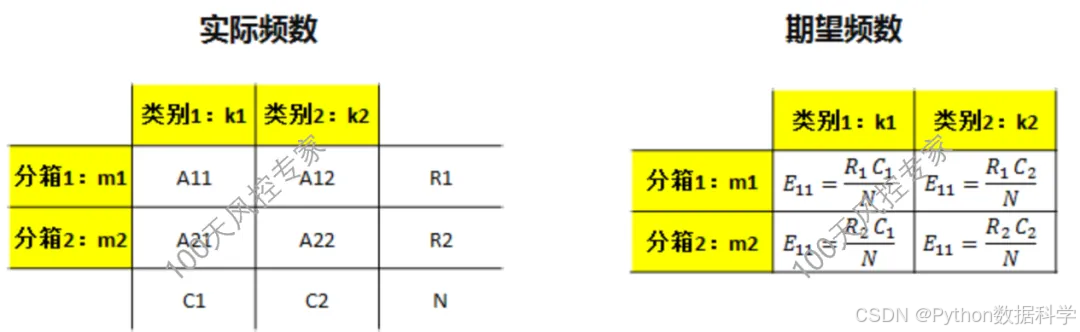
实际频数和期望频数都有了,带入卡方公式求解。如果计算结果是所有卡方值中最小的,说明:这组中两个分箱具有最相似的类分布,因此把它们合并。
注意:卡方分箱计算较为复杂,如数据量大、变量多的情况下可能会非常耗时,不建议使用。
完整介绍和代码参考👉《100天风控专家》
5. 最优分箱
1)Optbinning介绍
Optbinning开发了一种严谨且可扩展的数学规划公式。该通用公式能够高效地处理二进制、连续型和多类目标类型。对于这个三种目标类型,引入了一种"凸混合整数规划公式",从最简单的整数线性规划(ILP)公式到更复杂约束条件的混合整数二次规划(MIQP)公式不等。并且提出的公式不仅包含了通常用于生成良好分箱所需的约束条件,还涵盖了以前未处理的新约束条件。
2)Optbinning分箱步骤
最优分箱过程包含两个步骤:预分箱过程和优化过程,以满足施加的约束条件。
①预分箱过程:使用决策树算法来计算初始的分割点,得到的m个分割点按严格升序排列,即s1< s2 < ... < sm,以创建n= m + 1个预分箱。
②优化过程:通过各种约束条件来对分箱优化。不同目标类型约束条件不同,比如二分类约束条件包括:
a)单调性约束:三种单调趋势类型:上升/下降趋势,以及两种单峰形式,即凹/凸和峰/谷。
b)减少主导分箱:要求约束条件来限制分箱中(总/好/坏)的最大数量,防止任何一箱对结果产生过大的影响。也可以降低集中度指标(标准差、赫芬达尔-赫希曼指数以及最大分箱和最小分箱之间的差异)来生成更均匀的分箱。
c)最大p值约束:通过最大值p约束并确定一个显著性水平α,保证连续分箱之间具有统计学差异。比如统计检验方法包括Z检验、卡方检验等。
d)局部和启发式搜索的混合整数规划重制
官方教程链接:https://gnpalencia.org/optbinning/index.html
3)Optbinning代码实操
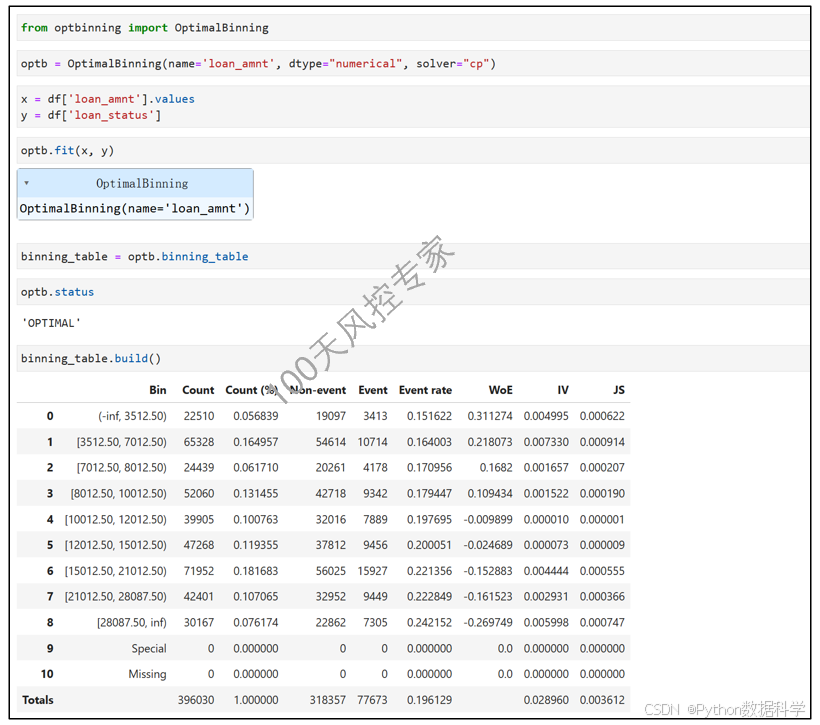
-- end
以上内容的完整讲解和数据代码(真实业务数据+代码实操)参考👉《100天风控专家》(共更新150期,涵盖业务、产品、策略、模型、数据等5大核心模块、10大专栏)