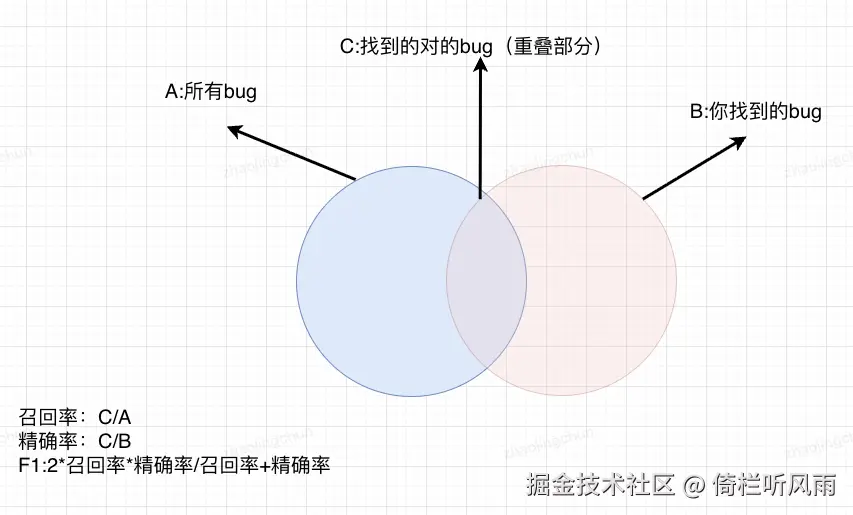
核心概念:混淆矩阵
要理解这三个指标,首先必须了解混淆矩阵。它描述了模型预测结果和真实结果之间的关系。
| 实际为正例 | 实际为负例 | |
|---|---|---|
| 预测为正例 | 真正例 (TP) | 假正例 (FP) |
| 预测为负例 | 假负例 (FN) | 真负例 (TN) |
- TP:预测为正,实际也为正。 (正确命中)
- FP:预测为正,实际为负。 (误报)
- FN:预测为负,实际为正。 (漏报)
- TN:预测为负,实际也为负。 (正确拒绝)
1. 精准率
-
核心问题 :在所有被模型预测为正例 的样本中,有多少是真的正例?
-
定义: Precision = TP / (TP + FP)
-
理解:
- 它关注的是预测结果的精确度。
- 高精准率意味着模型非常"谨慎",只有当它非常确定时,才会将一个样本预测为正例。因此,它的"误报"很低。
- 代价:可能会漏掉很多真正的正例(导致召回率低)。
应用场景 :在那些"误报成本高"的场景中,我们追求高精准率。
- 垃圾邮件检测:如果把一封正常邮件误判为垃圾邮件(FP),用户可能会错过重要信息,这是非常糟糕的。所以我们希望模型判断为"垃圾"的邮件,几乎100%都是垃圾。
- 推荐系统:我们希望推荐给用户的内容,尽可能都是他们感兴趣的。如果推荐了不相关的内容(FP),会影响用户体验。
2. 召回率
-
核心问题 :在所有真实为正例 的样本中,模型成功预测出了多少?
-
定义: Recall = TP / (TP + FN)
-
理解:
- 它关注的是模型发现正例的能力,也叫"查全率"。
- 高召回率意味着模型非常"敏感",能尽可能地找出所有真正的正例,不漏检。
- 代价:可能会把很多负例也错判为正例(导致精准率低)。
应用场景 :在那些"漏报成本高"的场景中,我们追求高召回率。
- 疾病检测(如癌症筛查):我们绝对不能放过任何一个真正的病人(FN)。即使把一些健康人误判为患者(FP),让他们去做进一步检查,也比漏掉一个癌症患者要好得多。
- 逃犯监控:在人群中识别逃犯,宁可错报(FP),也不能让真正的逃犯漏网(FN)。
3. F1分数
-
核心问题:如何同时兼顾精准率和召回率?
-
定义: F1 Score = 2 * (Precision * Recall) / (Precision + Recall)
-
理解:
- F1分数是精准率和召回率的调和平均数。
- 调和平均数相比算术平均数,更注重较小值。这意味着,只有当精准率和召回率都高时,F1分数才会高。
- 如果其中一个很低,就会严重拉低F1分数。
- 它是一个综合指标,用于在精准率和召回率之间寻找一个平衡点。
应用场景 :当我们需要一个单一的、综合的指标来评估模型性能,并且希望同时考虑精准率和召回率时。
- 当正负样本分布不平衡时,F1比准确率更有参考价值。
- 当你没有明确的倾向性(即不确定应该更看重精准率还是召回率)时,F1是一个很好的默认选择。