要理解DC/DC转换器的闭环稳定性设计逻辑 ,需结合小信号建模、传递函数分析 与波特图验证
一、闭环负反馈的基础作用:精度与响应的核心
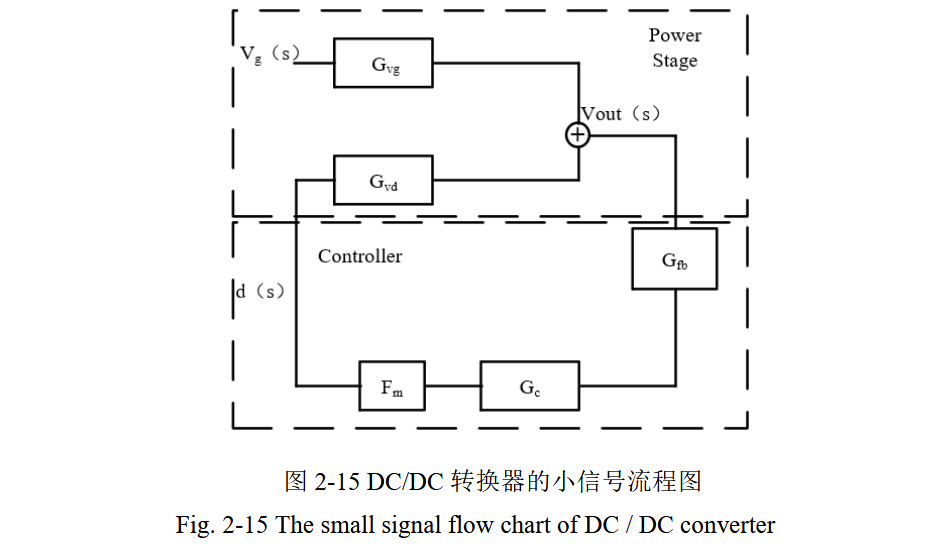
DC/DC转换器的核心是闭环负反馈(图2-15):
-
输出电压 Vout(s)经反馈网络 Gfb(s)(图2-19:Gfb=R1/(R1+R2))采样,与参考电压比较生成误差信号;
-
误差信号经调制网络 Fm(s)(图2-20:Fm=1/Vpp,Vpp为比较器翻转电压)、补偿网络 Gc(s)、功率级传递函数 Gvd(s)(图2-18:功率级的电感-电容谐振环节),最终调整功率管开关,稳定 Vout。
负反馈的本质是减小输出误差,提升电压精度;同时通过快速调整开关状态,改善动态响应(如负载突变时的电压恢复速度)。
二、未补偿时的稳定性问题:共轭极点与低相位裕度
功率级传递函数 Gvd(s)=1+sL/R+s2LCVg是二阶系统,对应电感 L与负载电容 C形成的谐振环节。其特征参数为:
-
共轭极点频率:ωp=LC1;
-
品质因数:Q=−C/LR。
Q为负且绝对值较大时,意味着功率级极点靠近jω轴,导致未补偿的开环传递函数 Floop(s)=Gvd(s)Gfb(s)Fm(s)出现两个关键问题:
-
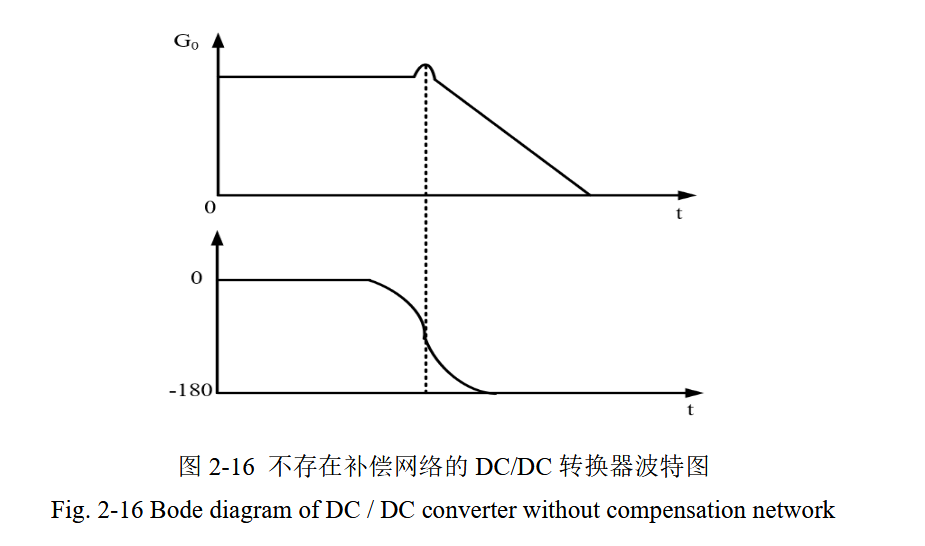
幅频谐振峰:图2-16上方子图显示,Floop(s)在 ωp处有明显尖峰(由谐振引起),导致增益波动;
-
相频快速下降 :图2-16下方子图显示,ωp处相位快速下降至-180°附近,相位裕度极低(相位裕度=180°+相频在增益穿越频率处的相位)。
未补偿的转换器相位裕度不足、单位增益带宽小 ,处于不稳定状态(易振荡或输出电压发散)。
三、频率补偿网络的作用:修改零点极点,提升稳定性
频率补偿网络 Gc(s)的核心是调整开环传递函数的零点/极点分布,抵消功率级的不良谐振特性,目标是:
-
降低功率级的 ∣Q∣值(减小极点与jω轴的距离);
-
提升相位裕度(通常要求≥45°);
-
优化增益穿越频率(保证响应速度)。
1. 补偿的数学逻辑:抵消极点/引入零点
功率级的二阶极点可表示为 s=−α±jωd(α=R/(2L),ωd=ωp2−α2)。补偿网络 Gc(s)若引入一个零点 s=−z,则开环传递函数的极点-零点对变为 (s+z)(s+α−jωd)(s+α+jωd)。零点会"抵消"部分极点的相位下降,降低 ∣Q∣,从而展宽相位裕度。
2. 基于波特图的设计验证
图2-16的波特图直观展示了未补偿时的不稳定:
-
幅频特性:ωp处的谐振峰导致增益波动;
-
相频特性:ωp处相位快速下降至-180°。
设计补偿网络后,需让波特图满足:
-
相位裕度≥45°:增益穿越频率处的相位需高于-135°(180°-45°);
-
抑制谐振峰:幅频特性的尖峰被削平,增益波动减小;
-
合适的单位增益带宽:保证负载突变时输出电压能快速恢复。
四、结论:补偿网络是稳定性的关键
常规DC/DC的闭环负反馈解决了精度与响应 问题,但功率级的二阶谐振特性导致不稳定。通过:
-
小信号建模(图2-15的流程图、各传递函数公式),明确开环传递函数的结构;
-
波特图分析(图2-16),定位不稳定的根源(共轭极点、低相位裕度);
-
频率补偿网络(Gc(s)),修改零点/极点分布,提升相位裕度。
最终实现DC/DC转换器的稳定运行,同时兼顾精度与响应速度。这也是电源设计中"补偿网络是环路稳定性核心"的根本原因。
相位裕度(Phase Margin, PM)
是控制系统中衡量稳定性的核心指标,其本质是系统在增益为0dB(单位增益)时 的相位与-180°的差值。以下从定义、物理意义、设计目标及工程应用四方面详细解读:
一、定义与数学表达
-
基本定义
相位裕度描述的是:当系统的开环增益等于1(即增益交点频率 ωc)时,其相位与-180°之间的差值。公式为:
\其中,∠G(jωc)表示开环传递函数在 ωc处的相位角。
-
几何意义
在波德图(Bode Plot)中,相位裕度对应以下两点:
-
增益交点:增益曲线与0dB线的交点频率 ωc;
-
相位交点:相位曲线与-180°线的交点频率 ω180。
相位裕度即为 ωc处的相位与-180°的差值。
-
二、物理意义:稳定性的"安全余量"
-
稳定性的量化指标
相位裕度反映系统在增益为1时的相位稳定性余量。若相位裕度为正值,说明系统在增益交点处的相位尚未达到-180°,此时系统仍稳定;若相位裕度为负值,则系统处于不稳定边缘。
-
抗扰动能力
相位裕度越大,系统对相位扰动(如负载突变、噪声干扰)的容忍度越高。例如:
-
相位裕度=45°:系统能承受一定程度的相位延迟而不振荡;
-
相位裕度=60°:系统稳定性更强,但响应速度可能降低。
-
-
与阶跃响应的关系
相位裕度直接影响闭环系统的动态响应:
-
相位裕度过小 (如<30°):阶跃响应可能出现过冲 和振荡;
-
相位裕度适中(如45°~60°):响应速度与稳定性达到平衡;
-
相位裕度过大(如>70°):系统响应变慢,可能无法快速跟踪输入信号。
-
三、设计目标与典型值
-
设计原则
相位裕度需在稳定性 与动态性能之间权衡:
-
稳定性优先:相位裕度应≥45°,避免系统振荡;
-
响应速度优先:可适当降低相位裕度(如30°~45°),但需确保系统仍稳定。
-
-
典型应用场景的相位裕度
场景 相位裕度范围 特点 通用运算放大器 45°~60° 平衡稳定性与响应速度 高速数据转换器 30°~45° 牺牲部分稳定性以提升带宽 电源管理芯片 60°~70° 优先抑制纹波和振荡
四、工程实现与补偿方法
-
补偿技术
通过调整系统传递函数的零极点分布,可改变相位裕度:
-
相位超前补偿:引入零点,提升中高频相位,增大相位裕度;
-
相位滞后补偿:引入极点,降低高频增益,避免相位裕度过小。
-
-
波德图分析工具
使用波特图可直观评估相位裕度:
-
增益曲线:检查0dB处的相位是否远离-180°;
-
相位曲线:观察是否在增益交点前出现陡峭下降(可能导致相位裕度不足)。
-
总结
相位裕度是控制系统稳定性的"安全余量",其设计需结合具体应用场景:
-
理论依据:通过波德图分析增益与相位的关系;
-
工程实践:利用补偿网络调整零极点,平衡稳定性与动态性能;
-
典型值参考:45°~60°为常见设计目标,需根据实际需求灵活调整。