平面几何：多边线光滑化处理

前端西瓜哥2025-10-28 10:04

大家好，我是前端西瓜哥。

今天来看看如何对多边线进行光滑处理。

多边线光滑化，指的是提供一个多边形和圆角半径值，将多边线的角点转换为圆弧，如下图所示。

image-20251012165457385

之前写过一篇文章，是关于 在两条直线相交处添加圆角 的算法，这其实就是我们今天要讲的多边线光滑化中的核心算法。

相比两条线段，多边线只是维度更高一点，需要做遍历，细节也多一些。

两直线相交处添加圆角

先回顾下之前文章写的 在两条直线相交处添加圆角算法。

原理是：

  1. 两条线段往内做距离为 radius 的偏移，求出交点；

  2. 交点到两条边做垂线，得到两个垂点，这两个点是圆角圆弧的起点和终点；

  3. 求出圆弧。

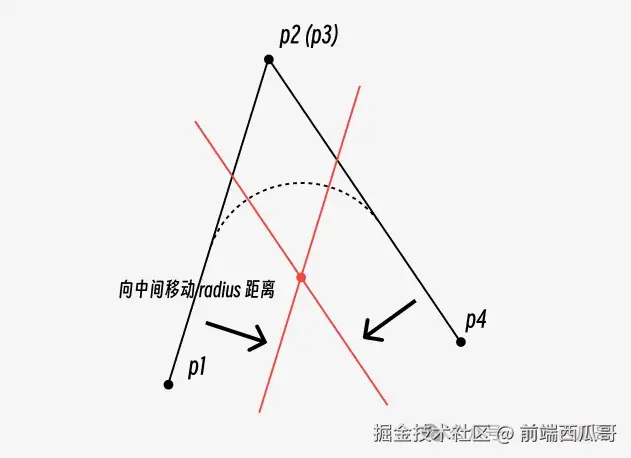
不过对于多段线，是多条线段组成的，radius 是受限的，不能无限大。

对此我们需要确定角点的可用圆角值 maxRadius。

maxRadius 确定

两条线段的情况下，一条线相邻边只有一条，它可以提供充分的空间给圆角线。

  1. 求相邻两条线段各自能支持的最大圆角半径，取其中较小的，作为半径的最大值 maxRadius；

  2. 将传入的 radius 限定在 [0, maxRadius] 范围；

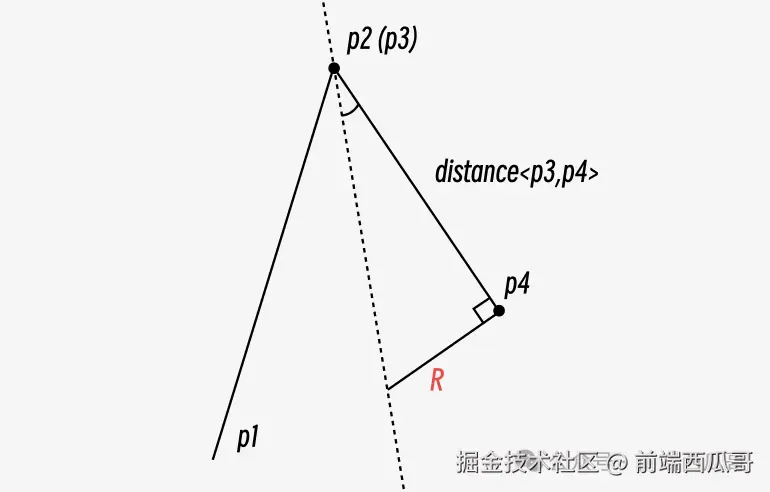
而在多边线场景下，一条线相邻边有两条边，这条边的两侧都要做圆角化。这就存在分配问题了，两边应分别分配多少空间？

一个简单且有效的策略是：平分。（多边线第一条边和最后一条边不需要做平分，因为它们只有一条相邻边。如果做了闭合，变成多边形的话，也是要平分的）

但是它是有个问题的，就是 不能充分利用空间。比如一个三角形，因为卡着边的中点的位置，所以大概率不能圆滑为这个三角形的内接圆。

如果希望想要充分利用空间，就需要类似三角形求圆心一样，求出 "圆心"，再去计算对应的利用空间。

如下图，要求 P 点圆角化最大半径，我们要先基于 P 和 Q 画出两条中线，求出 "圆心"，圆心对 PQ 线做垂线得到垂点 T，PT 就是给 P 的可用空间，另一边 QT 是 Q 的可用空间。

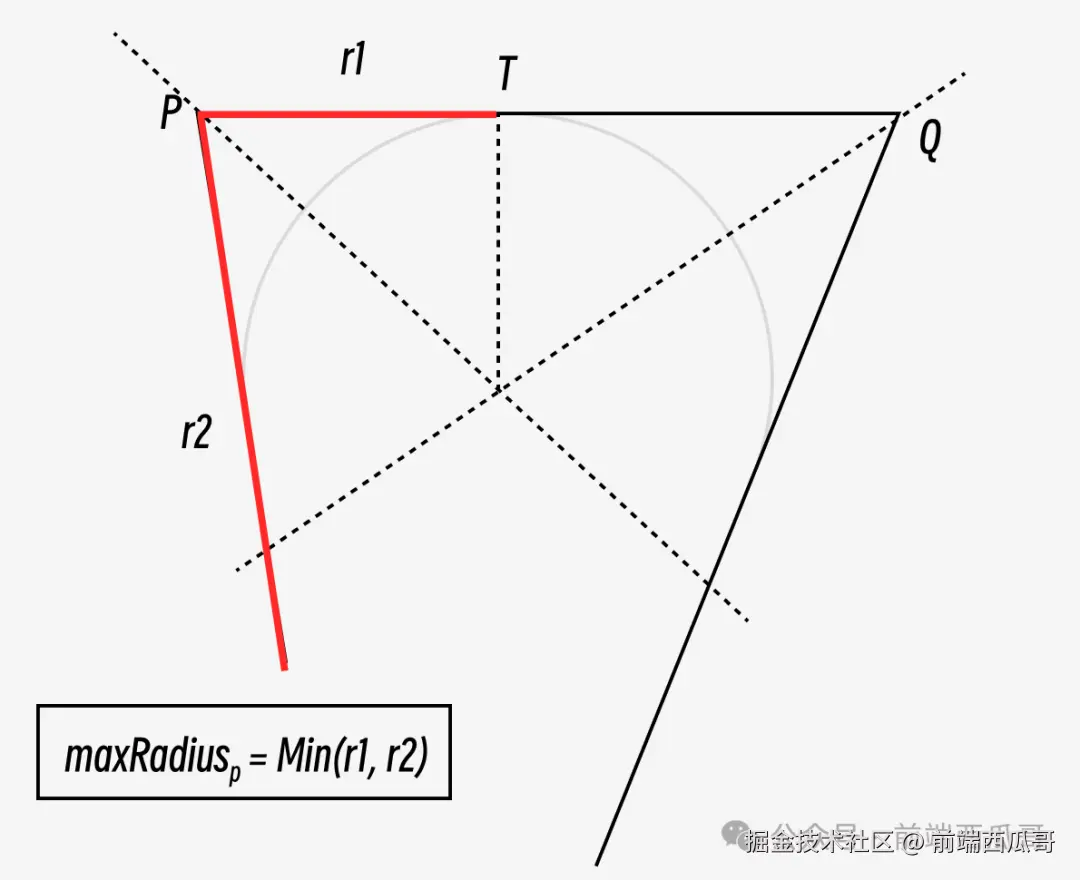
有个特殊情况，可能线不在相同方向，这时候需要将其中一条线翻转过来，这样才好求出 "圆心"。

这个还挺复杂的，我的需求也没这么高，所以这里我还是 继续用平分的方案。

这里只是稍微扩展一下，同时让读者理解为什么后面的实现 radius 开得很大，中间还是有直线的存在。感兴趣的读者可自行实现。

核心算法

ts 复制代码 
const roundPolyline = (polyline: Point[], radius: number) => {
let path: IPathCommand[] = [];
// 半径为 0 不做圆角化，以及小于 2 的话没有角点做圆角化
if (radius === 0 || polyline.length <= 2) {
    path = polyline.map((p) => ({
      type: 'L',
      points: [{ ...p }],
    }));
  } else {
    // 从索引为 1 开始，到倒数第 2 个点结束
    for (let i = 1; i < polyline.length - 1; i++) {
      const p1Index = i - 1;
      const p3Index = i + 1;

      const p1 = polyline[p1Index];
      const p2 = polyline[i];
      const p3 = polyline[p3Index];

      // 将 r 设置到正确的区间内
      const left = p1Index === 0 ? p1 : pointMid(p1, p2);
      const right = p3Index === polyline.length - 1 ? p3 : pointMid(p2, p3);
      const r = getCorrectedRadius(left, p2, right, radius);

      // 拿到圆角化数据，将它添加到 path 上
      const data = calcRoundCorner(p1, p2, p2, p3, r);

      if (data) {
        path.push({
          type: 'L',
          points: [{ ...data.start }],
        });

        const bezier = arcToBezier({
          center: data.circleCenter,
          r,
          startAngle: data.startAngle,
          endAngle: data.endAngle,
          angleDir: data.angleDir,
        });

        path.push({
          type: 'C',
          points: [bezier[1], bezier[2], bezier[3]],
        });
      } 
      // data 为 null，无法生成圆角
      else {
        path.push({
          type: 'L',
          points: [{ ...p2 }],
        });
      }
    }
  }

// 补充起点
if (!isPointEqual(path[0].points[0], polyline[0])) {
    path.unshift({
      type: 'L',
      points: [{ ...polyline[0] }],
    });
  }

if (
    !isPointEqual(
      path[path.length - 1].points.at(-1)!,
      polyline[polyline.length - 1],
    )
  ) {
    path.push({
      type: 'L',
      points: [{ ...polyline[polyline.length - 1] }],
    });
  }

  path[0].type = 'M';

return path;
};

效果

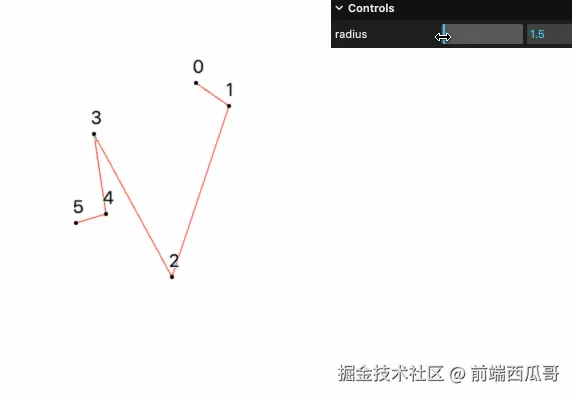
完整算法

核心算法调用的一些底层的基础几何方法，还挺多的。复杂算法本质就是一个个小的算法组合而成。

不过这些算法我在以前的文章都讲过，这里就不一一讲解了，具体哪些文章可以看文末的相关阅读。

ts 复制代码 
import { Matrix } from'pixi.js';

interface Point {
  x: number;
  y: number;
}

interface IPathCommand {
type: string;
  points: Point[];
}

exportconst roundPolyline = (polyline: Point[], radius: number) => {
let path: IPathCommand[] = [];
if (radius === 0 || polyline.length <= 2) {
    path = polyline.map((p) => ({
      type: 'L',
      points: [{ ...p }],
    }));
  } else {
    for (let i = 1; i < polyline.length - 1; i++) {
      const p1Index = i - 1;
      const p3Index = i + 1;

      const p1 = polyline[p1Index];
      const p2 = polyline[i];
      const p3 = polyline[p3Index];

      // 将 r 设置到正确的区间内
      const left = p1Index === 0 ? p1 : pointMid(p1, p2);
      const right = p3Index === polyline.length - 1 ? p3 : pointMid(p2, p3);
      const r = getCorrectedRadius(left, p2, right, radius);

      const data = calcRoundCorner(p1, p2, p2, p3, r);

      // data 为 null，说明无法生成圆角
      if (data) {
        path.push({
          type: 'L',
          points: [{ ...data.start }],
        });

        const bezier = arcToBezier({
          center: data.circleCenter,
          r,
          startAngle: data.startAngle,
          endAngle: data.endAngle,
          angleDir: data.angleDir,
        });

        path.push({
          type: 'C',
          points: [bezier[1], bezier[2], bezier[3]],
        });
      } else {
        path.push({
          type: 'L',
          points: [{ ...p2 }],
        });
      }
    }
  }

// 补充起点
if (!isPointEqual(path[0].points[0], polyline[0])) {
    path.unshift({
      type: 'L',
      points: [{ ...polyline[0] }],
    });
  }

if (
    !isPointEqual(
      path[path.length - 1].points.at(-1)!,
      polyline[polyline.length - 1],
    )
  ) {
    path.push({
      type: 'L',
      points: [{ ...polyline[polyline.length - 1] }],
    });
  }

  path[0].type = 'M';

return path;
};

const calcRoundCorner = (
  p1: Point,
  p2: Point,
  p3: Point,
  p4: Point,
  radius: number,
) => {
// p2 到 p1 向量
const v1 = {
    x: p1.x - p2.x,
    y: p1.y - p2.y,
  };

// p2 到 p3 的向量
const v2 = {
    x: p4.x - p3.x,
    y: p4.y - p3.y,
  };

// 求叉积
const cp = v1.x * v2.y - v2.x * v1.y;
if (cp === 0) {
    // 平行，无法生成圆角
    returnnull;
  }
let normalVec1: Point;
let normalVec2: Point;
// v2 在 v1 的左边
if (cp < 0) {
    // 求 v1 向左法向量
    normalVec1 = {
      x: v1.y,
      y: -v1.x,
    };
    // 求 v2 向右法向量
    normalVec2 = {
      x: -v2.y,
      y: v2.x,
    };
  }
// v2 在 v1 的右边
else {
    normalVec1 = {
      x: -v1.y,
      y: v1.x,
    };
    normalVec2 = {
      x: v2.y,
      y: -v2.x,
    };
  }

// 求沿法向量偏移半径长度的 line1
const t1 = radius / distance(p1, p2);
const d = {
    x: normalVec1.x * t1,
    y: normalVec1.y * t1,
  };
const offsetLine1 = [
    {
      x: p1.x + d.x,
      y: p1.y + d.y,
    },
    {
      x: p2.x + d.x,
      y: p2.y + d.y,
    },
  ];

// 求沿法向量偏移半径长度的 line1
const t2 = radius / distance(p3, p4);
const d2 = {
    x: normalVec2.x * t2,
    y: normalVec2.y * t2,
  };
const offsetLine2 = [
    {
      x: p3.x + d2.x,
      y: p3.y + d2.y,
    },
    {
      x: p4.x + d2.x,
      y: p4.y + d2.y,
    },
  ];

// 求偏移后两条直线的交点，这个交点就是圆心
const circleCenter = getLineIntersection(
    offsetLine1[0],
    offsetLine1[1],
    offsetLine2[0],
    offsetLine2[1],
  )!;

// 求圆心到两条线的垂足
const { point: start } = closestPointOnLine(p1, p2, circleCenter, true);
const { point: end } = closestPointOnLine(p3, p4, circleCenter, true);

// 圆心到垂足的弧度
const angleBase = { x: 1, y: 0 };
const startAngle = getSweepAngle(angleBase, {
    x: start.x - circleCenter.x,
    y: start.y - circleCenter.y,
  });
const endAngle = getSweepAngle(angleBase, {
    x: end.x - circleCenter.x,
    y: end.y - circleCenter.y,
  });

return {
    offsetLine1,
    offsetLine2,
    circleCenter,
    start,
    end,
    startAngle,
    endAngle,
    angleDir: cp < 0, // 正 -> 顺时针
  };
};

/** arc to cubic bezier */
const arcToBezier = ({
  center,
  r,
  startAngle,
  endAngle,
  angleDir = true,
}: {
  center: Point;
  r: number;
  startAngle: number;
  endAngle: number;
  angleDir: boolean;
}) => {
if (angleDir === false) {
    [startAngle, endAngle] = [endAngle, startAngle];
  }

const sweepAngle = (endAngle - startAngle + Math.PI * 2) % (Math.PI * 2);
const halfSweepAngle = sweepAngle / 2;
const k =
    (4 * (1 - Math.cos(halfSweepAngle))) / (3 * Math.sin(halfSweepAngle));

const matrix = new Matrix()
    .rotate(startAngle)
    .scale(r, r)
    .translate(center.x, center.y);

  endAngle -= startAngle;
  startAngle = 0;

const p1 = matrix.apply({
    x: 1,
    y: 0,
  });
const p2 = matrix.apply({
    x: 1,
    y: k,
  });

const p3 = matrix.apply({
    x: Math.cos(sweepAngle) + k * Math.sin(sweepAngle),
    y: Math.sin(sweepAngle) - k * Math.cos(sweepAngle),
  });

const p4 = matrix.apply({
    x: Math.cos(sweepAngle),
    y: Math.sin(sweepAngle),
  });

if (angleDir) {
    return [p1, p2, p3, p4];
  }
return [p4, p3, p2, p1];
};

/** 求两个向量的夹角 */
const getAngle = (a: Point, b: Point) => {
// 使用点乘求夹角
const dot = a.x * b.x + a.y * b.y;
const d = Math.sqrt(a.x * a.x + a.y * a.y) * Math.sqrt(b.x * b.x + b.y * b.y);
let cosTheta = dot / d;
// 修正精度问题导致的 cosTheta 超出 [-1, 1] 的范围
// 导致 Math.acos(cosTheta) 的结果为 NaN
if (cosTheta > 1) {
    cosTheta = 1;
  } elseif (cosTheta < -1) {
    cosTheta = -1;
  }
returnMath.acos(cosTheta);
};

/** 求两个点的中点 */
const pointMid = (p1: Point, p2: Point) => {
return {
    x: (p1.x + p2.x) / 2,
    y: (p1.y + p2.y) / 2,
  };
};

/** 求纠正后的半径 */
const getCorrectedRadius = (
  p1: Point,
  p2: Point,
  p3: Point,
  radius: number,
) => {
const v1 = {
    x: p2.x - p1.x,
    y: p2.y - p1.y,
  };
const v2 = {
    x: p2.x - p3.x,
    y: p2.y - p3.y,
  };
const angle = getAngle(v1, v2) / 2;

const r1 = Math.tan(angle) * distance(p1, p2);
const r2 = Math.tan(angle) * distance(p2, p3);
returnMath.min(radius, r1, r2);
};

const TOL = 0.00000001;
const isNumEqual = (a: number, b: number, tol = TOL) => {
returnMath.abs(a - b) <= tol;
};

const isPointEqual = (p1: Point, p2: Point, tol = TOL) => {
return isNumEqual(p1.x, p2.x, tol) && isNumEqual(p1.y, p2.y, tol);
};

const closestPointOnLine = (
  p1: Point,
  p2: Point,
  p: Point,
/** 是否限制在在线段之内 */
  canOutside = false,
) => {
if (p1.x === p2.x && p1.y === p2.y) {
    return {
      t: 0,
      d: distance(p1, p),
      point: { x: p1.x, y: p1.y },
    };
  }
const dx = p2.x - p1.x;
const dy = p2.y - p1.y;
let t = ((p.x - p1.x) * dx + (p.y - p1.y) * dy) / (dx * dx + dy * dy);
if (!canOutside) {
    t = Math.max(0, Math.min(1, t));
  }
const closestPt = {
    x: p1.x + t * dx,
    y: p1.y + t * dy,
  };
return {
    t,
    d: distance(p, closestPt),
    point: closestPt,
  };
};

const distance = (p1: Point, p2: Point) => {
const dx = p2.x - p1.x;
const dy = p2.y - p1.y;
returnMath.sqrt(dx * dx + dy * dy);
};

/**
 * 求向量 a 到向量 b 扫过的夹角
 * 这里假设为 x时针方向为正
 */
const getSweepAngle = (a: Point, b: Point) => {
// 使用点乘求夹角
const dot = a.x * b.x + a.y * b.y;
const d = Math.sqrt(a.x * a.x + a.y * a.y) * Math.sqrt(b.x * b.x + b.y * b.y);
let cosTheta = dot / d;
// 修正精度问题导致的 cosTheta 超出 [-1, 1] 的范围
// 导致 Math.acos(cosTheta) 的结果为 NaN
if (cosTheta > 1) {
    cosTheta = 1;
  } elseif (cosTheta < -1) {
    cosTheta = -1;
  }

let theta = Math.acos(cosTheta);
// 通过叉积判断方向
// 如果 b 在 a 的左边，则取负值
if (a.x * b.y - a.y * b.x < 0) {
    theta = -theta;
  }

return theta;
};

/**
 * 求两条直线交点
 */
const getLineIntersection = (
  p1: Point,
  p2: Point,
  p3: Point,
  p4: Point,
): Point | null => {
const { x: x1, y: y1 } = p1;
const { x: x2, y: y2 } = p2;
const { x: x3, y: y3 } = p3;
const { x: x4, y: y4 } = p4;

const a = y2 - y1;
const b = x1 - x2;
const c = x1 * y2 - x2 * y1;

const d = y4 - y3;
const e = x3 - x4;
const f = x3 * y4 - x4 * y3;

// 计算分母
const denominator = a * e - b * d;

// 判断分母是否为 0（代表平行）
if (Math.abs(denominator) < 0.000000001) {
    // 这里有个特殊的重叠但只有一个交点的情况，可以考虑处理一下
    returnnull;
  }

const px = (c * e - f * b) / denominator;
const py = (a * f - c * d) / denominator;

return { x: px, y: py };
};

线上 demo

stackblitz.com/edit/vitejs...

结尾

我是前端西瓜哥，关注我，学习更多几何知识。

相关阅读，

在两条直线相交处添加圆角，算法该如何实现？

平面几何：求向量 a 到向量 b扫过的夹角

你知道吗？圆弧有3种表达方式

解析几何：计算两条线段的交点

平面几何算法：求点到直线和圆的最近点

相关推荐
老前端的功夫3 小时前
Webpack 优化：你的构建速度其实还能快10倍
前端·javascript
Holin_浩霖3 小时前
React渲染原理学习笔记
前端
OpenTiny社区3 小时前
我用3 分钟上手 RankProcessChart 排名进度图！
前端·github
十里八乡有名的后俊生3 小时前
从在线文档崩溃说起-我的前端知识管理系统搭建之路
前端·开源·github
_光光3 小时前
任务队列及大文件上传实现（前端篇）
前端·react.js·typescript
残冬醉离殇3 小时前
缓存与同步：前端数据管理的艺术
前端
前端西瓜哥3 小时前
常用的两种填充策略：fit 和 fill
前端
Lsx_3 小时前
ECharts 全局触发click点击事件（柱状图、折线图增大点击范围）
前端·javascript·echarts
不吃香菜的猪4 小时前
构建时变量注入：Vite 环境下 SCSS 与 JavaScript 的变量同步机制
前端·javascript·scss
热门推荐
01GitHub 镜像站点02BongoCat - 跨平台键盘猫动画工具03UV安装并设置国内源04GitLab 零基础入门指南：从安装到项目管理全流程05Linux下V2Ray安装配置指南06NVIDIA显卡驱动、CUDA、cuDNN 和 TensorRT 版本匹配指南07Labelme从安装到标注：零基础完整指南08Burp与其他安全工具联动及代理设置教程09jdk21下载、安装（Windows、Linux、macOS）10Pycharm+Neo4j红楼梦人物关系图谱