MCU定点计算深度解析：原理、技巧与实现

摘要

在嵌入式系统中，微控制器单元（MCU）通常仅支持整数运算，这为处理小数或浮点数据带来了挑战。定点计算作为一种高效的数值处理方法，能够在整数硬件上实现近似浮点运算的精度，广泛应用于信号处理、控制算法等领域。本文从定点计算的基本原理入手，深入解析其数学基础，并结合实际MCU编程场景，分享实用技巧与优化方法。文章内容涵盖定点数的表示、运算规则、缩放因子选择、溢出处理及代码实现，旨在帮助开发者在不支持浮点单元的MCU上实现高效数据处理。全文基于严谨的工程实践，公式采用LaTeX格式，以增强可读性与专业性。

关键词：MCU、定点计算、整数运算、数据处理、嵌入式系统、缩放因子

---

1. 引言

MCU在物联网、工业控制和消费电子等领域应用广泛，但其硬件资源往往有限，许多低成本MCU仅支持整数运算单元（ALU），无法直接处理浮点数。浮点运算通常需要软件模拟或专用硬件，这会导致性能下降和代码膨胀。定点计算通过将小数映射到整数域，利用整数运算模拟小数行为，成为一种高效的替代方案。例如，在PID控制器、数字滤波器或音频处理中，定点计算能显著提升效率。本文将从原理出发，系统介绍定点计算的核心概念，并提供实用的编程技巧，帮助读者在资源受限的MCU上实现精确计算。

---

2. 定点计算原理

定点计算的核心思想是将小数表示为整数，并通过缩放因子（Scaling Factor）来隐含小数点的位置。假设一个实数 x 被表示为定点数，其格式通常定义为 Qm.n，其中 m 表示整数部分位数，n 表示小数部分位数，总位数固定（如16位或32位）。例如，在Q15.16格式中，一个32位整数的高16位表示整数部分，低16位表示小数部分。

2.1 定点数表示

给定一个实数 x，其定点表示可通过缩放因子 2n 转换为整数 X：

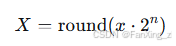
其中，n 为小数位数，X 为存储的整数值。还原实数时：

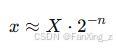
例如，将实数 3.14 转换为Q15.16格式（n=16）：

还原时：

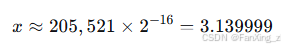
误差由截断或舍入引起，需在设计中权衡精度与范围。

2.2 定点运算规则

定点数的加法和乘法需调整缩放因子，以避免精度损失和溢出。

• 加法 ：要求操作数具有相同的缩放因子。若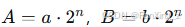，则：

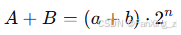
直接整数加法即可，但需注意溢出。

int32_t result = (int32_t)A * B;  // 中间结果可能为64位
result >>= n;  // 右移n位调整缩放因子

• 除法：较复杂，需左移被除数以提高精度。若 D=A/BD，则：

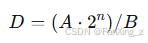
这些运算的误差主要来源于舍入和溢出，需通过选择合适的 nn 和数据类型来管理。

---

3. 实用技巧

在实际MCU应用中，定点计算的效率与精度取决于多个因素，以下为关键技巧。

3.1 缩放因子选择

缩放因子 2^n 的选择需平衡动态范围和精度：

• 精度：n 越大，小数部分分辨率越高，例如 n=16 时，最小分辨率为 2−16≈1.5×10−5。

• 范围：n 越小，整数部分范围越大。例如在16位MCU中，若 n=8，则整数范围为 [−128,127]，小数精度为 2^(−8)=0.0039。

• 动态范围可通过公式估算：

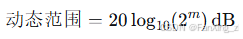
其中 m 为整数部分位数。实践中，需根据应用需求调整。例如，在音频处理中，Q15.16格式可覆盖-1到1的幅度范围；而在电机控制中，可能需Q8.8格式以处理更大整数。

3.2 溢出处理

整数运算易溢出，尤其在乘法和累加中。解决方法包括：

• 使用更大数据类型：例如在16位MCU上，用32位整数存储中间结果。

• 饱和运算（Saturation Arithmetic）：当结果超出范围时，钳制到最大值或最小值。例如：

  int32_t sat_add(int32_t a, int32_t b) {
      int64_t tmp = (int64_t)a + b;
      if (tmp > INT32_MAX) return INT32_MAX;
      if (tmp < INT32_MIN) return INT32_MIN;
      return (int32_t)tmp;
  }

• 缩放调整：在运算前预缩放数据，减少溢出风险。

3.3 精度优化

• 舍入策略：乘法右移时，采用四舍五入而非截断。例如：

  int32_t multiply_round(int32_t a, int32_t b, int n) {
      int64_t tmp = (int64_t)a * b;
      tmp += (1 << (n - 1));  // 加入舍入偏移
      return (int32_t)(tmp >> n);
  }

• 误差分析：通过统计方法评估累积误差，在迭代算法（如滤波器）中尤为重要。

---

4. 编程技巧

在MCU编程中，定点计算需注意代码效率和可维护性。以下以C语言为例，展示常见实现。

4.1 数据类型定义

使用typedef定义定点类型，便于统一管理：

typedef int32_t fixed_t;  // 定义32位定点数
#define FIXED_SHIFT 16    // 小数位数n=16
#define FLOAT_TO_FIXED(x) ((fixed_t)((x) * (1 << FIXED_SHIFT)))
#define FIXED_TO_FLOAT(x) ((float)(x) / (1 << FIXED_SHIFT))

这简化了定点数与浮点数的转换。

4.2 基本运算实现

• 加法：直接操作，但需确保操作数缩放因子一致：

  fixed_t fixed_add(fixed_t a, fixed_t b) {
      return a + b;  // 可能溢出，需检查范围
  }

• 乘法：使用64位中间结果避免溢出：

  fixed_t fixed_multiply(fixed_t a, fixed_t b) {
   int64_t tmp = (int64_t)a * b;
   tmp += (1 << (FIXED_SHIFT - 1)); // 四舍五入 
  return (fixed_t)(tmp >> FIXED_SHIFT); 
  }

• 除法：左移被除数以提高精度：

  fixed_t fixed_divide(fixed_t a, fixed_t b) {
      int64_t tmp = (int64_t)a << FIXED_SHIFT;
      return (fixed_t)(tmp / b);
  }

4.3 优化技巧

• 内联函数 ：在性能关键路径使用inline关键字减少函数调用开销。

• 查表法：对于复杂函数（如三角函数），预计算定点值表，以空间换时间。

• 编译器优化：利用MCU编译器的特性，如ARM CMSIS-DSP库中的定点函数。

4.4 实例：定点PID控制器

以下为一个简单的定点PID实现，适用于电机控制：

typedef struct {
    fixed_t kp, ki, kd;
    fixed_t integral;
    fixed_t prev_error;
} pid_controller_t;

fixed_t pid_update(pid_controller_t *pid, fixed_t error) {
    fixed_t p_term = fixed_multiply(pid->kp, error);
    pid->integral = sat_add(pid->integral, error);
    fixed_t i_term = fixed_multiply(pid->ki, pid->integral);
    fixed_t derivative = error - pid->prev_error;
    fixed_t d_term = fixed_multiply(pid->kd, derivative);
    pid->prev_error = error;
    return sat_add(p_term, sat_add(i_term, d_term));
}

此代码通过定点运算避免浮点开销，并集成饱和处理。

---

5. 结论

定点计算是MCU处理小数数据的有效方法，它通过整数运算和缩放因子实现了精度与效率的平衡。本文系统阐述了定点数的表示原理、运算规则及实用技巧，并提供了可移植的代码示例。在资源受限的嵌入式系统中，合理应用定点计算可显著提升性能，同时避免浮点硬件的依赖。开发者需根据具体应用动态调整缩放因子，并注意溢出和误差管理。未来，随着MCU性能提升，定点计算仍将在低功耗和实时性要求高的场景中发挥关键作用。

---

参考文献

1. ARM Limited. CMSIS-DSP Library Documentation. 2022.

2. Oppenheim, A. V., & Schafer, R. W. Discrete-Time Signal Processing. Pearson, 2010.

3. Embedded Systems Academy. Fixed-Point Arithmetic in C. 2021.