双指针是算法中一种常用的技巧,特别适用于数组和链表类问题。它的核心思想是使用两个指针以不同的策略遍历数据结构,从而高效地解决问题。
双指针常见的三种类型:
(1)快慢指针:两个指针从同一侧开始移动,但移动速度不同。
适用范围:这种⽅法对于处理环形链表或数组⾮常有⽤。
实现方式:快慢指针的实现方式有多种,但常见的是在⼀次循环中,每次让慢的指针向后移动⼀位,⽽快的指针往后移动两位,实现⼀快⼀慢。
下面的例题会解析快慢指针的用法:
核心思想:
这个代码中我们会用到两个指针,一个fast指针一个slow指针,快指针用来遍历整个数组,而慢指针用来指向非0的位置,遇到非0元素+1即可
class Solution {
public:
void moveZeroes(vector<int>& nums)
{
int slow = -1;
int fast = 0;
for(;fast < nums.size();fast++)
{
if(nums[fast])
{
swap(nums[++slow],nums[fast]);
}
}
}
};(2)左右指针(对撞指针):两个指针分别指向序列的开头(左)和结尾(右),然后向中间移动,直到它们相遇。
特点:指针移动方向是相对的。
适用范围:主要适用于数组和字符串,通常要求序列是有序的。
来一道例题来解析对撞指针的用法: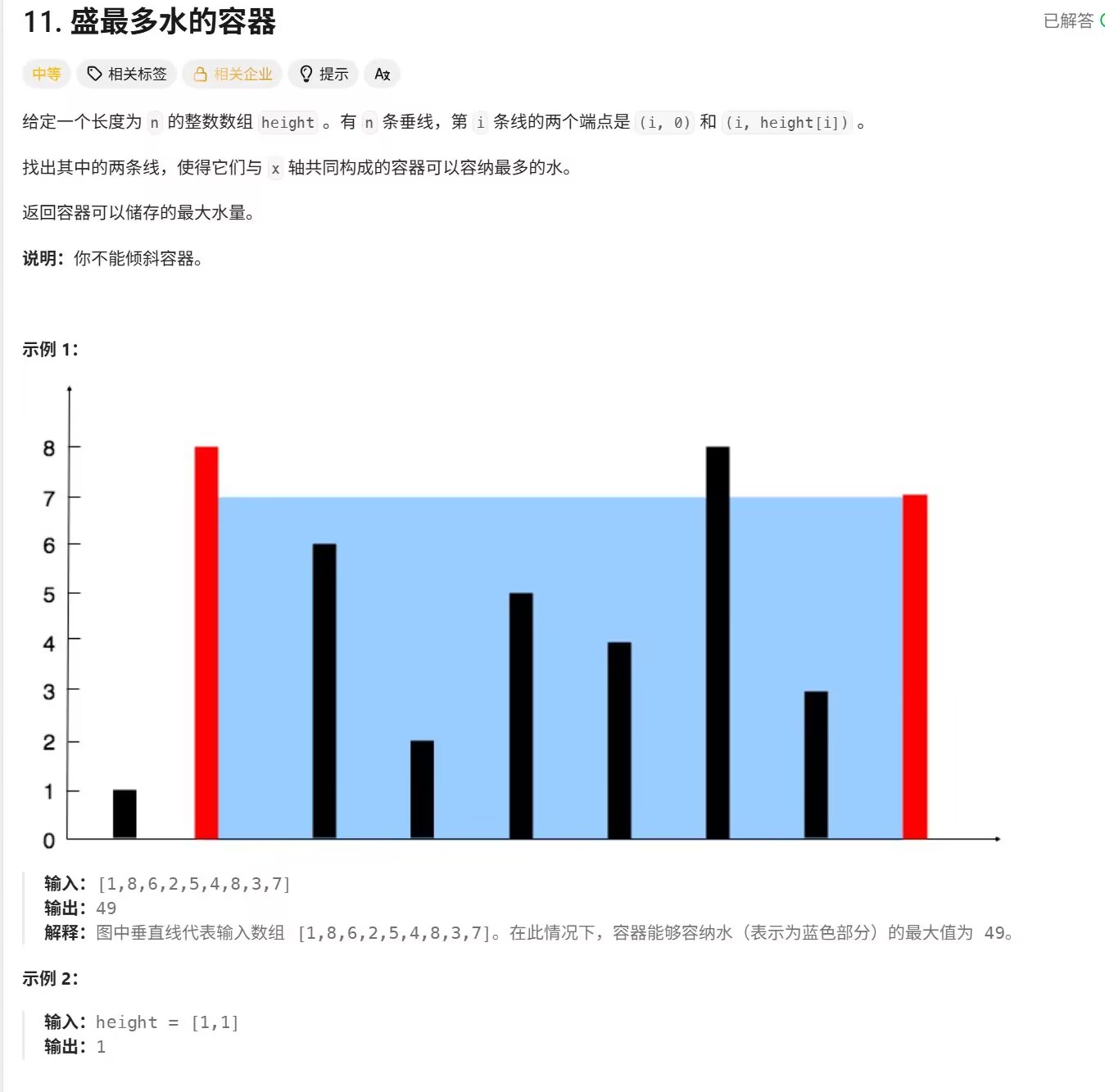
class Solution {
public:
int maxArea(vector<int>& height)
{
int left = 0;
int right = height.size() - 1;
int ret = 0;
while(left < right)
{
int high = min(height[right],height[left]);
int width = right - left;
int nowret = high * width;
ret = max(ret,nowret);
if(height[right] > height[left])
{
left++;
}
else
{
right--;
}
}
return ret;
}
};这道题让我们求承最多水的容器,也就是求面积最大的区域,所以这道题我们应该找出面积最大的区域。我们可以先定义出一个left和一个right用来表示height数组中的最左侧位置和最右侧位置,然后我们通过min来比较谁的高度比较小并且与距离相乘用来求出当前区域的面积。然后与最大的面积相比留下最大的面积,随后我们比较right和left所对应的数组元素的高度,较小的一方缩进数组,随后再重复以上方法,进而比较出面积最大的区域。
为什么要移去较小边界的那一端呢?
因为当我们移动较高边界那一端时,最低的高度不变,反而宽度减小,这样并不会生成面积更大的数组,反而当我们把数组较小的那一端移去,虽然宽度减小,但是有可能高度会增加,进而产生的面积可能比原来的最大面积更大。
(3)滑动窗口:滑动窗口是双指针的一种高级用法,两个指针形成一个窗口(区间),通过移动左右指针来动态地维护这个窗口,从而解决问题。
适用场景:寻找满足某种条件的连续子数组或子字符串(如:最小覆盖子串、长度最小的子数组、无重复字符的最长子串。)。
核心思想:
1.right指针向右扩张窗口,直到窗口内的元素满足条件。
2.然后 left指针向右收缩窗口,同时更新最优解,直到窗口不再满足条件。
3.重复步骤 1 和 2,直到 right到达末尾。
例题:
class Solution {
public:
int minSubArrayLen(int target, vector<int>& nums)
{
int left = 0;
int right = 0;
int sum = 0;
int min_len = INT_MAX;
for(;right < nums.size();right++)
{
sum += nums[right];
while(sum >= target)
{
min_len = min(min_len,right - left +1);
sum -= nums[left];
left++;
}
}
return (min_len == INT_MAX ? 0 : min_len);
}
};我们定义两个指针 left和 right,初始都指向数组的起始位置。再定义出定义 sum记录当前窗口的和,min_len记录最小长度。随后将 nums[right]加到 sum中,表示扩展窗口的右边界。right向右移动,直到 sum >= target。当 sum >= target时,尝试收缩窗口的左边界:计算当前窗口的长度 right - left + 1,并更新 min_len。将 nums[left]从 sum中减去,然后 left右移。重复此过程,直到 sum < target(窗口不再满足条件)。当 right遍历完整个数组后,返回 min_len。如果 min_len未被更新(即没有满足条件的子数组),返回 0。
为什么滑动窗口有效,并且时间复杂度更低呢?
因为这个数组都是正整数,这意味着我们向右扩展窗口时,数组内元素之和是严格递增的,当我们向右收缩窗口时,数组内元素之和也是严格递减的。不会出现反复回溯的情况。通过left和right两个指针,滑动窗口可以不遗漏任何可能的连续的子数组。避免了暴力解法中的重复计算。通过每次发现 sum >= target,记录当前窗口的长度并且进行比较,一旦 sum < target就停止收缩直接扩展窗口避免无效计算。
时间复杂度:虽然代码是两层循环,但是我们的 left 指针和 最多都往后移动 n 次。因此时间复杂度是 O(N) 。