系列文章目录
为了帮助大家蓝桥杯取得好成绩,专门写一篇蓝桥杯省赛题解,帮助大家寻找解题思路
前言
题解大部分会写在代码中,除了一些比较难的
提示:以下是本篇文章正文内容,下面案例可供参考
一、题目列表
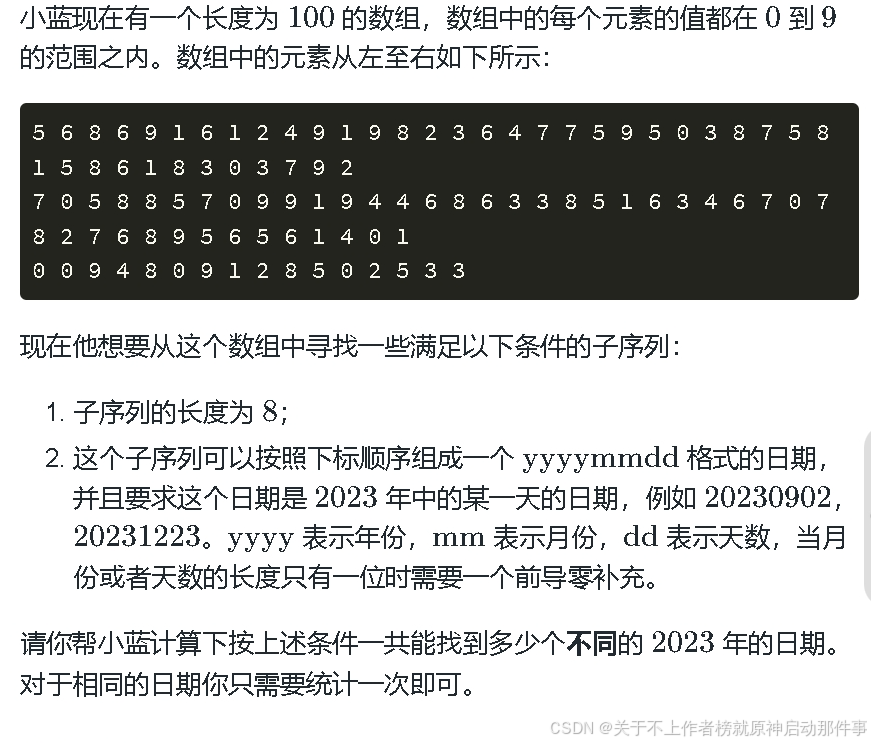
1.日期统计
2.01串的熵·
3.冶炼金属
4.飞机降落
5.接龙序列
6.0岛屿个数
7.整数删除
二、题解
1.日期统计
思路
考察知识:日期的基本常识,和模拟全部解的思想。当我们发现从题目给的条件里去找答案会形成很多可能的时候,我们就可以考虑使用dfs深度优先搜索,或者模拟全部解。这个题目要求我们从这个数组中去寻找可能出现的天数,直接去找显然不可能,我们尝试去看所有解的情况,也就365天的情况,所以我们遍历所有的月份天数,比从给的数组里面去找合适的天数要简单的多。
代码解释
这份代码包含了对数组的两种处理方式,字符串和数组。
因为闰年的二月份天数不同,所以先处理。
to_string()是将转化为字符串的函数,返回值是字符串而不是字符
最后是前导0的处理,对于字符串我们直接加上"0"即可,对于数组2 0 2 3 0 5 0 8,就是八个数字我们给前导0留一个位置即可,很多人被前导0卡住,但是只要换一种思路即可对于一个两位数分为个位和十位,对于小于10的数来说十位就是0,大于10,十位就是x/10。
代码
#include <iostream>
using namespace std;
int main()
{
int a[100]={5,6,8,6,9,4,6,4,5,4,9,1,9,8,2,3,6,4,7,7,5,9,5,0,3,8,7,5,8,1,5,8,6,1,8,3,0,3,7,9,2,7,0,5,8,8,5,7,0
,9,9,1,9,4,4,6,8,6,3,3,8,5,1,6,3,4,6,7,0,7,8,2,7,6,8,9,5,6,5,6,1,4,0,1,0,0,9,4,8,0,9,1,2,8,5,0,2,5,3,3};
// 因为100个随机组合很多,要从里面找出日期不可取,我们可以遍历所有天数,在数组里面查看有没有。,为了方便我们使用字符串
// string s="5686916124919823647759503875815861830379270588570991944686338516346707827689565614010094809128502533";
// 定义日期
int day[13]={0,31,28,31,30,31,30,30,30,30,31,30,31};
if(2023%4==0&&2023%100!=0||2023%400==0) day[1]+=1;
int ans=0;
// 遍历2023年的所有天,在字符串里面查看有没有
for(int i=1;i<13;i++)
{
for(int j=1;j<=day[i];j++)
{
// 字符串解法
// string y=to_string(i);
// string d=to_string(j);
// if(i<10) y="0"+y;
// if(j<10) d="0"+d;
// string p="2023"+y+d;
// int o=0;
// for(int k=0;k<s.size();k++)
// {
// if(s[k]==p[o]) o++;
// if(o==8)
// {
// ans++;
// break;
// }
// }
int b[8]={2,0,2,3,i/10,i%10,j/10,j%10};
int l=0;
for(int k=0;k<100;k++)
{
if(a[k]==b[l]) l++;
if(l==8)
{
ans++;
break;
}
}
}
}
cout<<ans;
return 0;
}2.01串的熵

思路
这个题看似简单,其实坑非常多,很难一次做对,不过收获也很多。
其实和上面题一个思路,我就不对说,模拟就行,但是要注意的几个点有
1.对公式的理解 2.精度判断,在计算这种小数的时候,经常会出现精度损失的情况,所以要和答案一模一样是基本不可能的,所以我们只需要计算他们的差值在一个范围内就行。比如这道题,小数有四位,我们只需要计算他们的差值在0.0001以内就可以,其实0.1左右就行。
既然思路普通,但是我们可以从里面学到什么
1.模拟所有解的思想
2.在进行小数位数很多的计算,可能会出现精度损失导致与答案不一样,面对这种情况我们就要进行误差判断,
3.数学函数的运用log(2),对于一般的数学公式利用math.h就可以直接调用。
4.二分的运用,这个代码里面讲,相当于一个优化。
最后对于公式的理解,我建议自己带入几个值,小一点,就知道公式展开是什么样的了,因为这个最好的办法就是自己带入几个值看看公式是怎么样计算的,题目给的不行,反而误导了我。
代码
#include <iostream>
#include <math.h>
#include <iomanip>
#define eps 0.0001
using namespace std;
int main()
{
int n = 23333333;
for (int i = 1; i < n; i++)
{
if (i >= n - i) break;
double a = 1.0 * i / n;
double b = 1.0 * (n - i) / n;
double p = a * log2(a), q = b * log2(b);
double sum = 0.0;
sum -= p * i + q * (n - i);
if (abs(sum - 11625907.5798) < eps)
{
//cout << fixed << setprecision(5) << sum << '\n';
cout << i << '\n';
return 0;
}
}
return 0;
}
法二
//二分优化代码
二分通常用在顺序数组里面,寻找某个值,这题刚好合适,寻找某个值,但要注意的是0,1,的个数对s影响的。这里0越少s越小。单调性判断大家都会吧。
#include<bits/stdc++.h>
using namespace std;
#define ll long long
double p(ll x,ll y){ //x 0 y 1
double P0 = 1.0*x/(x+y);
double P1 = 1.0*y/(x+y);
return -1.0*x*x/(x+y)*log2(P0)-1.0*y*y/(x+y)*log2(P1);
};
int main(){
ll n = 23333333;
ll l=1, r=(n-1)/2;
double PP = 11625907.5798;
二分模板,如果会按照自己的来就行,每个人写法不一样。
while(l<r){
int mid = (l+r)>>1;
double t = p(mid, n-mid);
if(t<PP) l=mid+1;
else r=mid;
}
cout << l << endl;
return 0;
}3.冶炼金属

思路:感觉这个题没有什么难度,最重要的就是理解题意,看懂题,题目要求我们找的v必须要符合所有数据,一开始我们还是一样的进行模拟,模拟所有v,但是发现v是一个规律进行递增的,结合我们需要找到某个值,这完全符合二分查找的思想,直接套用就行了。很简单的一道模板题目。
#include <bits/stdc++.h>
using namespace std;
int a[10005];
int b[10005];
int n;
// int mins=0;
// int maxs=0;
//判断当前v符不符合最小。
bool chack_min(int k)
{
for(int i=0;i<n;i++)
{
//这里可能有人不理解为什么要>,v越小得到的b就越大,但是最大肯定不能超过给的数据,不然就没有意义了,直接选v==1不就好了,看测试样例也可以看出来,最大最小v都是符合给的数据的
if(a[i]/k>b[i]) return false;
}
return true;
}
//判断符不符合最大
bool chack_max(int k)
{
for(int i=0;i<n;i++)
{
if(a[i]/k<b[i]) return false;
}
return true;
}
//找最小的v
int chack_mins()
{
int l=1;
int r=100000000;
int mins=0;
while(l<=r)
{
int mid=(l+r)>>1;
//要保证每个v都符合所有数据
if(chack_min(mid))
{
mins=mid;
r=mid-1;
}
else
{
l=mid+1;
}
}
return mins;
}
//找最大的v
int chack_maxs()
{
int l=1;
int r=100000000;
int maxs=0;
while(l<=r)
{
int mid=(l+r)>>1;
//要保证每个v都符合所有数据
if(chack_max(mid))
{
maxs=mid;
l=mid+1;
}
else
{
r=mid-1;
}
}
return maxs;
}
int main()
{
//根据题目要求,要我们找到符合所以数据的v,并且要找v的最大值和最小值,说明v的取值是一个区间
//最简单的放发也是一样的模拟所以v的可能。对于最小的v,要保证得到的b不超过给的b。
//既然是顺序的模拟,那么我们可以用二分去优化复杂度。
// for(int i=0;i<=le9;i++)
// {
// }
cin>>n;
for(int i=0;i<n;i++)
{
cin>>a[i]>>b[i];
}
// chack_maxs();
int mins=chack_mins();
int maxs=chack_maxs();
cout<<mins<<" "<<maxs;
return 0;
}4.飞机降落
 78
78
思路
这届蓝桥杯很多模板题,这也是一道dfs模板题。大部分题都可以用搜索,主要是超时问题,
dfs几个条件
1.结束条件 2.约束条件3.递归条件4.标记数组5.回溯,了解这几个在多练习几道题一般的dfs都会写。
结束条件,从题目中我们可以知道当降落的飞机为n的时候结束,而如果始终不能降落完所有飞机就输出false。我这里使用一个bool数据用来判断
bool gg=false;
if(x==n)
{
gg=true;
return;
}
约束条件
我们访问过的飞机不能访问了,这就需要一个标记数组,第二个是飞机能不能降落,题目中也说明了
if(!flag[i])
{
if(tt[i]+dd[i]>=last)
{
flag[i]=true;
dfs(x+1,max(tt[i],last)+ll[i]);
if(gg) return;
flag[i]=false;
}
递归条件,就是飞机降落的条件
last是上一个飞机的最晚降落时间,那么我们肯定要当前飞机的降落区间大于last或者包含last
对于大于last,当前飞机的最早降落时间大于last肯定就在tt[i]时刻降落,对于包含last的时候,就是当前飞机降落的时间区间包含last那么我们肯定就在last时刻进行降落,因为我们要保证飞机尽可能早降落,所有只需要比较tt[i]和last的大小1就行了。
if(tt[i]+dd[i]>=last)
{
flag[i]=true;
dfs(x+1,max(tt[i],last)+ll[i]);
if(gg) return;//找到了就没有必要找了;
flag[i]=false;
//最后注意回溯
代码
#include <iostream>
using namespace std;
//数据非常小,多半是dfs
//x表示降落飞机数量,last表示当前最晚降落时间
int n;
int tt[10];
int dd[10];
int ll[10];
bool flag[10];
bool gg;
void dfs(int x,int last)
{
if(x==n)
{
gg=true;
// cout<<55;
return;
}
for(int i=0;i<n;i++)
{
if(!flag[i])
{
if(tt[i]+dd[i]>=last)
{
flag[i]=true;
dfs(x+1,max(tt[i],last)+ll[i]);
if(gg) return;
flag[i]=false;
}
// else
// {
// return;
// }
}
// return;
}
}
int main()
{
//模板提,dfs遍历所有情况。
int t;
cin>>t;
while(t--)
{
cin>>n;
for(int i=0;i<10;i++) flag[i]=false;
for(int i=0;i<n;i++)
{
cin>>tt[i]>>dd[i]>>ll[i];
}
gg=false;
dfs(0,0);
if(gg==true)
{
cout<<"YES"<<endl;
}
else{
cout<<"NO"<<endl;
}
}
return 0;
}5. 接龙序列

思路
对于这个题感觉出的很可以,对于学习动态规划是一道好题,首先简单描述一下动态规划,就是当前解可以由前一个解求出,比如我们要找2023字串,那么2023是不是由202字串加3得出的,那么假如给我们一个很长的字符串,当我们遍历到3的时候,我们只需要加上202字串的个数,那么这个题也是一样的。
这个题我们建立动态规划数组dp[i],就是以当前数字为开头找后面可以形成接龙的数字.
转移方程就是
for(int i=0;i<v.size();i++)
{
string l=v[i];
string m;
for(int j=i+1;j<v.size();j++)
{
m=v[j];
if(l[l.size()-1]==m[0])
{
//如果可以形成接龙序列,首先我们要明确我们要找最长的,所以我使用max来进行比较如果形成的接龙序列长度比原来的多那么就更新dp
dp[j]=max(dp[j],dp[i]+1);
}
}
}
带入数据11 121 22 12 2023
对于11 可以形成接龙的有 下标(从0开始)i= 1 ,3。那么dp[1]=dp[0]+1,dp[3]=dp[0]+1;
初始都为1,dp数组,
对于121 可以形成接龙的有 i=3,dp[3]=max(dp[1]+1,dp[3]);其实上面也是这个但是是第一次比较就没写,这里dp[3]在第一次就形成了接龙长度为2,但是在这里又形成了接龙而且dp[1]+1=3更长了所以更新,那么这就是最简单的暴力动态规划。对于这个题只能得一半的分。
所以我们在仔细观察发现,当我们遍历到某个数的时候,比如121,我们要找的是121前面以1结尾的最长接龙序列加1,就是121可以形成的最长序列,他代表的就是以他数字最后一位结尾的最长序列,
比如123 就是代表以三结尾的最长子序列他等于以1结尾的最长接龙序列加一,当然只有比本身大都时候才更新。
dp[3]=max(dp[1]+1,dp[3]);
转移方程就是
int dp[10]={0};//表示以i结尾的最大序列长度
for(int i=0;i<n;i++)
{
cin>>a;
int l=a[0]-'0';
int r=a[a.size()-1]-'0';
dp[r]=max(dp[l]+1,dp[r]);
}
的
代码
#include <bits/stdc++.h>
using namespace std;
// long long n;
// long long maxx=0;
// int main()
// {
// cin>>n;
// vector<string> v;
// string s;
// vector<long long> dp(n+5,1);
// for(int i=0;i<n;i++)
// {
// cin>>s;
// v.push_back(s);
// }
// for(int i=0;i<v.size();i++)
// {
// string l=v[i];
// string m;
// for(int j=i+1;j<v.size();j++)
// {
// m=v[j];
// if(l[l.size()-1]==m[0])
// {
// dp[j]=max(dp[j],dp[i]+1);
// }
// }
// }
// for(int i=0;i<n;i++)
// {
// maxx=max(maxx,dp[i]);
// }
// cout<<n-maxx;
// return 0;
// }
int dp[10]={0};//表示以i结尾的最大序列长度
int main()
{
int n;
string a;
cin>>n;
for(int i=0;i<n;i++)
{
cin>>a;
int l=a[0]-'0';
int r=a[a.size()-1]-'0';
dp[r]=max(dp[l]+1,dp[r]);
}
int res=0;
for(int i=0;i<10;i++)
{
res=max(res,dp[i]);
}
cout<<n-res;
}6.0岛屿个数
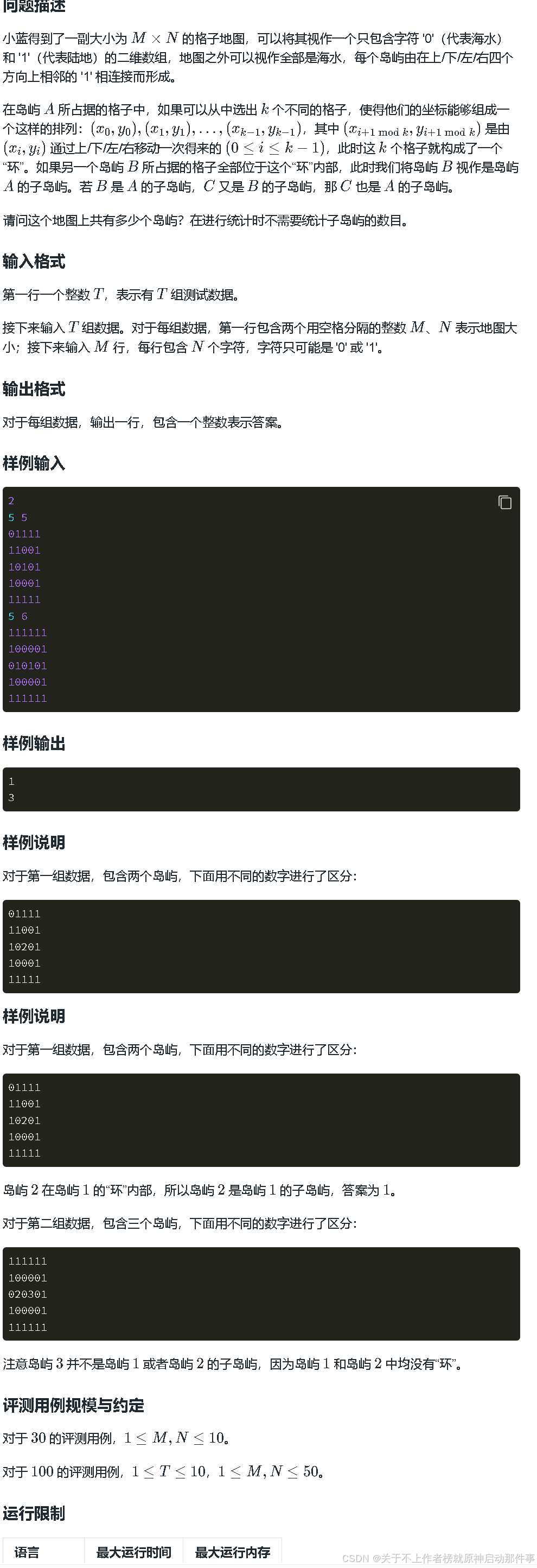
思路
这个题想清楚了其实很简单,要我们找外面没有环的岛屿,从里面往外面找很难写,暂时没有想到,但是我们可以从外面向里面找,让海水去流动,如果岛屿是一个环的情况,我们海水是进不去的,所以大体思路就是从外面一圈海水的地方去搜索,遇到一个岛进行答案记录,然后进行dfs或者bfs去找相邻的岛,全部标记,这样就标记了一个岛屿,
下面这个代码外面先bfs遍历所有的海水,海水有八个方向而岛只有4跟方向,很考验细心的一道题,并不好写。
非常注意的一个点就是外面必须先输入字符然后在变成数字,非常阴间。
代码
#include<bits/stdc++.h>
using namespace std;
int g[55][55];
int m,n,ans;
bool sea[55][55];
bool road[55][55];
//方向向量
//水流动八个方向
int seax[8]={-1,-1,-1,0,1,1,1,0};
int seay[8]={-1,0,1,1,1,0,-1,-1};
int roadx[4]={-1,0,1,0};
int roady[4]={0,1,0,-1};
//检测越界函数
bool chack(int x,int y)
{
if(x>=0&&x<m&&y>=0&&y<n)
{
return true;
}
else
{
return false;
}
}
void bfs_road(int x ,int y)
{
// queue<pair<int,int>> q;
// q.push({x,y});
// road[x][y]=true;
// while(q.size())
// {
// auto x=q.front();
// q.pop();
// for(int i=0;i<4;i++)
// {
// int mx=x.first+roadx[i];
// int my=x.second+roady[i];
// if(chack(mx,my)&&g[mx][my]==1&&!road[mx][my])
// {
// road[mx][my]=true;
// q.push({mx,my});
// }
// }
// }
//dfs写法上面是bfs写法
for(int i=0;i<4;i++)
{
int mx=x+roadx[i];
int my=y+roady[i];
if(chack(mx,my)&&g[mx][my]==1&&!road[mx][my])
{
road[mx][my]=true;
bfs_road(mx,my);
// road[mx][my]=false;
}
}
// return;
}
void bfs_sea(int x,int y)
{
queue<pair<int,int>> q;
q.push({x,y});
sea[x][y]=true;
while(q.size())
{
auto x=q.front();
q.pop();
for(int i=0;i<8;i++)
{
int mx=x.first+seax[i];
int my=x.second+seay[i];
if(chack(mx,my)&&!g[mx][my]&&!sea[mx][my])
{
sea[mx][my]=true;
q.push({mx,my});
}
if(chack(mx,my)&&g[mx][my]&&!road[mx][my])
{
ans++;
road[mx][my]=true;//如果用dfs必需加上这一句,仔细看dfs里面的语句发现遍历的这个点没有进行标记,用bfs不用写了,
bfs_road(mx,my);
}
}
}
}
int main()
{
int t;
cin>>t;
while(t--)
{
cin>>m>>n;
ans=0;
for(int i=0;i<=m;i++)
{
for(int j=0;j<=n;j++)
{
sea[i][j]=false;
road[i][j]=false;
}
}
char c;
for(int i=0;i<m;i++)
{
for(int j=0;j<n;j++)
{
cin>>c;
g[i][j]=c-'0';
}
}
//寻找外海
bool flag=false;//处理全是岛屿的情况;
for(int i=0;i<m;i++)
{
for(int j=0;j<n;j++)
{
if(i==0||i==m-1||j==0||j==n-1)
{
if(!g[i][j]&&!sea[i][j])
{
flag=true;
bfs_sea(i,j);
}
}
}
}
if(flag) cout<<ans<<endl;
else
{
cout<<1<<endl;
}
}
}
