这是一个关于信号数字化与传输的核心知识体系。
从采样开始，因为这是数字化的第一步。采样定理的核心是奈奎斯特频率，这里容易混淆，得强调采样频率必须大于两倍最高频率，而不是大于等于。不然重建信号会失真。
然后联系到奈奎斯特准则，这里用户可能混淆了采样定理和准则的区别。需要解释准则更多是针对码间干扰，在数字基带传输中的应用，而采样定理是针对模拟到数字的转换。
接着是PCM，它是实际应用采样定理的例子，包含采样、量化、编码三步。用户可能想知道理论怎么应用到实际，比如电话系统为什么用8kHz采样，量化噪声怎么产生，编码怎么用A律十三折线压缩。
一、采样与采样定理
采样是将连续时间的模拟信号转换为离散时间信号的过程。具体来说，就是以固定的时间间隔（采样周期 Ts）从模拟信号中抽取瞬时幅值，形成一系列在时间上离散的数据点。
-
采样频率 (fs)：每秒采样的次数，fs=1/Ts，单位是赫兹（Hz）。
-
采样后的信号：只在离散时间点 nTs（n为整数）上有定义。
核心问题：采样会丢失原始连续信号在采样点之间的信息吗？采样后得到的离散信号能否无失真地还原回原始模拟信号？
奈奎斯特-香农采样定理
采样定理完美地回答了上述问题，它是整个数字信号处理领域的基石。
定理内容：一个频率带宽限制在 fm Hz 以内的模拟信号，当采样频率 fs≥2fm 时，可以由其采样得到的离散信号完全唯一地重建出来。
-
fm：原始模拟信号中的最高频率成分。
-
2fm：被称为 奈奎斯特频率 (Nyquist Rate)。
-
fs/2：被称为 奈奎斯特频率 (Nyquist Frequency) 或折叠频率，这是一个非常重要的边界。
混叠现象
如果采样定理的条件不被满足，即 fs<2fm，会发生什么？
会发生混叠。
-
解释：高频信号成分在采样后，会"伪装"成低频信号。在频域上看，频谱会发生重叠，导致无法通过滤波器将原始频谱分离出来，从而在重建信号时引入无法消除的失真。
-
直观例子（车轮效应）：在电影中，有时会看到高速旋转的车轮看起来像是在缓慢倒转。这是因为电影的帧率（相当于采样频率）不足以捕捉车轮的实际转速，产生了视觉上的"混叠"。
为了避免混叠，在实践中：
- 抗混叠滤波器：在采样之前，必须使用一个低通滤波器（抗混叠滤波器）将原始模拟信号中高于 fs/2 的频率成分强行滤除，确保进入采样器的信号满足带宽限制条件。
二、奈奎斯特准则
请注意，"奈奎斯特准则"这个术语在通信系统中通常有两种相关但略有区别的语境。
采样定理本身
有时，人们会将采样定理中 fs≥2fm 的要求称为奈奎斯特准则。这是对采样定理条件的另一种称呼。
数字基带传输的无码间串扰准则
在数字通信（特别是基带传输）中，奈奎斯特准则特指一种用于消除码间串扰 的准则。
-
问题：在发送端，我们将离散的采样点（已经是数字脉冲）发送出去。由于信道带宽有限，脉冲在传输过程中会被展宽，以至于当前脉冲的"尾巴"会延伸到后续脉冲的时间段内，干扰后续脉冲的判决。这就是码间串扰。
-
奈奎斯特第一准则（无码间串扰准则）：
如果整个通信系统（包括发送滤波器、信道、接收滤波器）的总体冲激响应满足：在每个采样时刻（除了自身脉冲的中心点），其他所有脉冲的响应值都为0，那么就没有码间串扰。
-
奈奎斯特带宽：为了实现无码间串扰，系统所需的最小理论带宽是符号率 (Rs) 的一半，即 Bmin=Rs/2 Hz。例如，要无失真地传输 1 Mbps 的二进制信号，理论上至少需要 500 kHz 的带宽。
小结
-
采样定理 解决的是模拟信号到离散信号的转换与重建问题。
-
奈奎斯特准则（ISI） 解决的是离散数字符号在带宽受限信道中传输的失真问题。
两者都体现了哈利·奈奎斯特的开创性贡献，都涉及带宽与速率的基本限制。
三、脉冲编码调制（PCM）
PCM 是将模拟信号数字化的一套完整技术方案，而采样是其中的第一步。它是现代数字通信（如电话、CD、计算机音频）的基础。
PCM 过程包含三个核心步骤：
步骤一：采样
- 如上所述，按照奈奎斯特采样定理，以频率 fs 对模拟信号进行采样，得到时间上离散但幅度上连续的采样保持信号（PAM信号）。
步骤二：量化
将采样得到的连续幅度值，四舍五入到最接近的、预先设定的离散电平上。
问题：量化过程会引入永久的误差，称为量化误差或量化噪声。这个误差是无法消除的。
量化电平数 (L)：将信号的动态范围划分为 L 个离散电平。
量化位数 (n)：每个量化电平可以用一个 n 位的二进制码来表示，关系为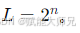
。
- 例如，8位量化，有
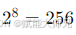电平；16位量化，有
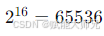个电平。
量化精度：位数 n 越高，量化电平越密集，量化误差越小，信噪比越高，但数据量也越大。
步骤三：编码
-
将每一个量化后的电平值，用一个对应的 n 位二进制码组表示出来。
-
最终得到的输出就是一串串的二进制比特流（例如
01001101...），这就是数字信号。
整个PCM过程产生的数据速率（比特率）为：
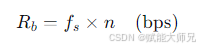
例如，电话系统：
语音带宽 fm≈4kHz，采样频率 fs=8kHz（满足 > 2*4kHz）。
采用 8 位（n=8）量化。
所以，一路标准电话语音的 PCM 数据速率为 8kHz×8bit=64kbps。这就是数字通信中著名的"64k信道"的由来。
四、总结
| 概念 | 核心问题 | 关键参数/准则 | 在PCM中的作用 |
|---|---|---|---|
| 采样与采样定理 | 如何保证离散时间信号能无失真重建为连续信号？ | 采样频率 fs≥2fm （奈奎斯特频率） | PCM的第一步。确定了从时间上离散化信号的规则，决定了每秒需要多少个样本。 |
| 奈奎斯特准则 | 如何保证离散数字符号在带宽受限信道中无失真传输？ | 系统带宽 B≥Rs/2 | 决定了PCM数字流在信道中传输时所需的最小理论带宽。 |
| 脉冲编码调制(PCM) | 如何将模拟信号完整地转换为数字信号？ | 三步曲：采样 -> 量化 -> 编码 | 一整套数字化方案。它综合利用了采样定理（解决时间离散）和量化编码（解决幅度离散）。 |
采样定理 为PCM的采样步骤提供了理论保障 -> PCM执行采样、量化、编码，生成二进制比特流 -> 这个比特流在信道中传输时，需要遵循奈奎斯特准则（ISI） 来避免码间串扰，从而可靠地到达接收端。