【CUDA笔记】05 使用 AMGX 实现泊松图像编辑

引言

前几节已经根据入门课程，了解了一些 CUDA 的使用技巧。这一节想先跳出原本的课程节奏，找点实际的应用，来看看能否从另一个角度练习一下 CUDA。

最后找到了话题 实现泊松图像编辑。

类似如下的抠图编辑为泊松图像编辑应用的一种。

输入：

输出：

网上可以找到不少介绍泊松图像编辑的参考文章，也可以先参考一下，了解原理与一些其他的应用

图像处理基础（九）泊松图像编辑 Possion Image Editing: https://zhuanlan.zhihu.com/p/453095752

泊松图像编辑(Possion Image Edit)原理、实现与应用： https://blog.csdn.net/weixin_43194305/article/details/104928378

不少文章的起点是 2003 年的这篇论文

《Poisson Image Editing》: https://www.cs.jhu.edu/~misha/Fall07/Papers/Perez03.pdf

本节尝试使用基于 CUDA 实现的AMGX 库，求解泊松方程，来实现泊松图像编辑。

主要梳理 泊松图像融合的原理 ， 如何使用 AMGX ，与本地试验结果。

泊松图像融合的原理

泊松图像融合的大致思想 是，当我们有一张前景图，一张背景图，一张通过标记前景图中感兴趣的区域（后面简称 ROI ）后生成的 Mask 图, 通过最小化 前景图与背景图在ROI 范围内的像素梯度值的差异，实现前景图像 ROI 区域无缝地融合到背景图像中。进而通过求导函数 = 0 ，取函数极值的思路，将求最小值问题转化为求导函数 = 0 的解。

前置概念

梯度（Gradient）

个人理解， 这里梯度表示图像某个通道像素值沿着某个方向（x 或 y）的变化速度。每个像素对应一个向量，表示包含沿着x 与 y 方向的变化速率。

常用于边缘检测（使用 Sobel 算子）

散度（Curl）

散度衡量向量场在某一点"发散"或"汇聚"的程度。

在图像处理中，可以使用拉普拉斯算子来计算图像梯度的散度。

拉普拉斯算子

在数字图像中，像素是离散的，通常用卷积核来近似拉普拉斯算子。常见的 3×3 拉普拉斯核包括：

构建线性方程组 A * f = b

问题描述

设：

Ω⊂Z2：要融合的前景区域（掩码区域），是一个连通的像素集合；
∂Ω：区域 Ω 的边界（即与背景接触的像素）；
f (x ,y )：前景图像（source image），定义在包含 Ω 的区域上；
g (x ,y )：背景图像（target image），定义在整个图像域上；
目标：构造一个新图像

u (x ,y)

，满足：
- 在 Ω 内部，u 保留 f 的梯度结构（即纹理、细节）；
- 在 ∂Ω 上，u =g（即与背景无缝拼接）。

核心思想

将通过泛函的知识，将上述问题等价为求解泊松方程

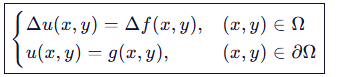
其中：

u 是 Ω 内所有未知像素值组成的向量；（也就是小标题里提到的 f，该解向量将包含融合区域内我们所有需要的解 f(x,y)）
A 是离散拉普拉斯矩阵（五点 stencil，对角占优）；
b 包含 Δf 和来自边界的 g 值。

可用共轭梯度法（CG）、多重网格法等高效求解。

扩展：混合梯度（Mixed Gradient）

此时构建方程组右端的尝试项时，便不可直接对前景图应用拉普拉斯算子来求解，而需要对该像素所在位置，在两幅图上沿着各个方向求出梯度，根据筛选条件选出四个方向（四个方向是对应前面的五点取样方法）的梯度值之后，再计算散度，得到混合的右端项。

求解线性方程组 A * f = b

由于 A 是大型稀疏对称正定矩阵（在 Dirichlet 条件下），常用以下数值方法求解：

1. 共轭梯度法（Conjugate Gradient, CG）

适用于对称正定系统；
内存效率高，适合大图像；
是泊松融合中最常用的迭代法之一。

2. Jacobi / Gauss-Seidel 迭代

算法基础信息可参考：https://zhuanlan.zhihu.com/p/389389672

简单易实现；
收敛慢，一般只用于教学或小图。

3. 多重网格法（Multigrid Method）

算法基础信息可参考 https://zhuanlan.zhihu.com/p/337970166

收敛速度极快（接近 O(n)）；
实现较复杂，但性能优越；
常用于实时或高性能图像编辑软件。

4. 直接法（如稀疏 LU 分解）

对小区域可行；
大图内存消耗大，不实用。

使用 AMGX 求解线性方程组

AMGX（Advanced MultiGrid eXtensions）是由NVIDIA开发的一个高效、可扩展的库，专门用于解决大规模稀疏线性方程组。它特别适用于需要高性能计算的应用场景，如物理模拟、图像处理、机器学习等。AMGX通过利用GPU的强大并行计算能力，提供了解决复杂计算问题的有效手段。

源码地址： https://github.com/NVIDIA/AMGX

这次练习使用的是截自目前最新的 Release 版本， AMGX v2.4.0 (也已经是 23年了)

Cuda 12.4 （虽然AMGX Release 日志里说是支持到 12.2，但处理一下，走下来，依赖 12.4 也是可以编译过）

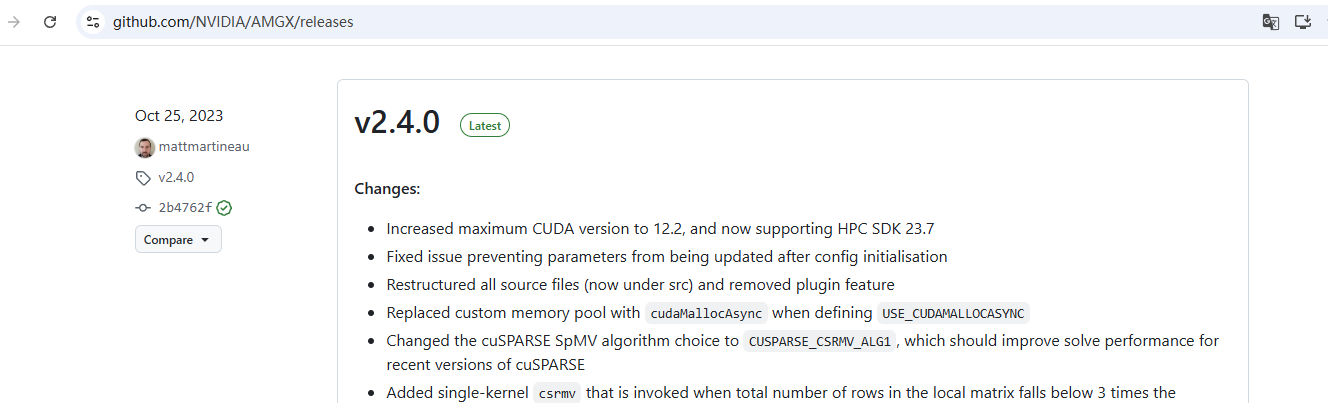
Visual Studio 2022 ， win11

子模块 Trust 没有下载源码仓库对应的版本，暂时直接使用的 CUDA Toolkit 中自带的版本（使用源码仓库对应的版本，出现了与 CUDA 版本的兼容问题，编译不过。这边尝试，在执行 cmake 指令之前，将 CMakeList.txt 的这一行注释掉，以使用 CUDA Toolkit 中的版本）。

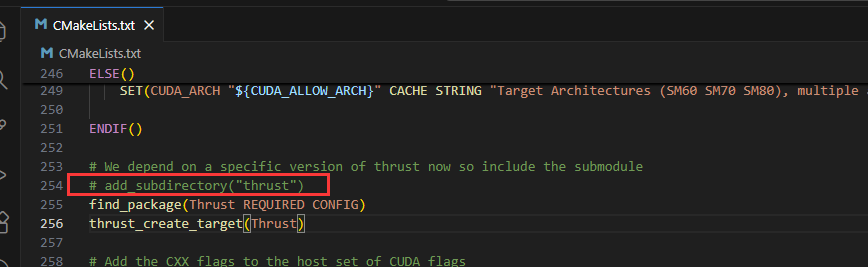
编译依赖库

代码拉下之后，在项目代码根目录下一次执行如下指令

复制代码

mkdir build
cd build
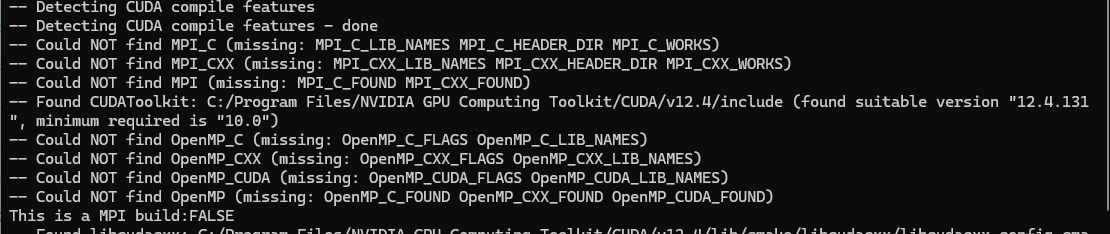
cmake ../
make -j16 all

执行 cmake 指令的过程中可能会遇到如下 missing 的提示。我这边因为暂时没有使用到 MPI 的特性（可以在多个 GPU 或多个计算节点 上分布式求解大型稀疏线性方程组），先忽略跳过。

生成的 AMG.sln 包含一以下几个项目中，

其中， amgx 项目生成静态链接库

， amgxsh 项目生成动态链接库，供运行时加载

本次试验中，生成动态库 amgxsh 这个项目。

生成成功后，把 AMGX 源码中的 include 与动态库挑出来出来就可以用了。

稀疏矩阵的存储格式

在该问题中的矩阵A，通常是稀疏矩阵（大部分元素是 0），前人们设计了一些格式，来节省矩阵存储空间，优化存储效率。

因为这里借助 AMGX 求解问题，会使用到 CSR 格式来存储矩阵，作为数据输入。所以这里补充一下 CSR 格式的基本信息。

values 数组（假设长度为 N）：

存储矩阵中所有非零元素的值。
这些值按照从上到下、从左到右的行遍历顺序排列。

colIndices 数组（长度也为 N）：

与 values 数组长度相同，用于存储 values 中每个元素对应的列索引。
例如，如果 values 中的第 k 个元素是矩阵第 i 行、第 j 列的非零元素，那么 colIndices 中的第看个元素就是 j。

rowPointers 数组(长度为 Matrix 行数 + 1)：

长度为矩阵行数加一，用于指示每一行的第一个非零元素在 values 数组中的起始位置。
rowPointers[i] 记录的是第 i 行第一个非零元素在 values 中的索引。
惯例上，rowPointers 数组的最后一个元素（即 rowPointers[n]，其中 n 是矩阵的行数）通常存储为非零元素的总数 N 加上 1，这标志着最后一行元素的结束。

举个例子

考虑一个 4×4 矩阵：

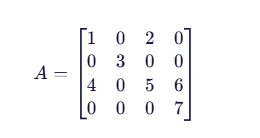
步骤 1：按行遍历非零元

第 0 行：1（列0）、2（列2）

第 1 行：3（列1）

第 2 行：4（列0）、5（列2）、6（列3）

第 3 行：7（列3）
步骤 2：构建三个数组

数组内容

values $1, 2, 3, 4, 5, 6, 7$

colIndices $0, 2, 1, 0, 2, 3, 3$

rowPointers $0, 2, 3, 6, 7$

本地试验结果

试验项目源码地址： https://github.com/CC9701/possionImageEditing

试验日志

复制代码

[Time] 1. 读取图像 elapsed: 13 ms
All images loaded successfully.
Background size: [614 x 461]
Foreground size: [400 x 300]
Mask size: [400 x 300]
Warning: Image sizes do not match! Poisson fusion requires same dimensions.
Number of foreground pixels: 40800
[Time] 4. 构建线性方程组 Af = b elapsed: 45 ms
Linear system constructed successfully.
NonZeroValueVec size: 199952
Column index size: 199952
Row pointer size: 40801
AMGX version 2.4.0
Built on Nov 26 2025, 21:23:18
Compiled with CUDA Runtime 12.4, using CUDA driver 13.0
[Time]  5. 使用 AMGX 求解线性方程组 单个通道 elapsed: 1003 ms
[Time]  5. 使用 AMGX 求解线性方程组 三个通道 elapsed: 2365 ms
All three channels solved successfully.
[Time]  6. 合成结果图像 elapsed: 1 ms

融合结果

未使用梯度混合

可以看到飞机周围的一圈还是有一点糊
使用梯度混合

也可以根据实际情况再拓展一下梯度混合的方式，比如混合梯度筛选梯度时，看看如何给不同来源的梯度值分配胜选的权重。