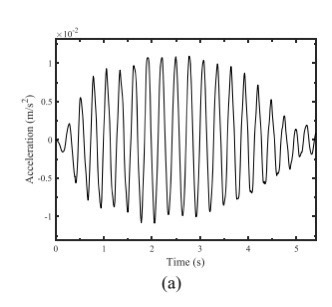
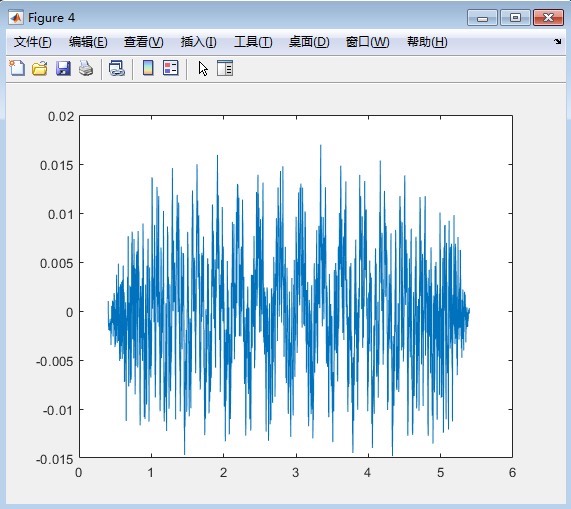
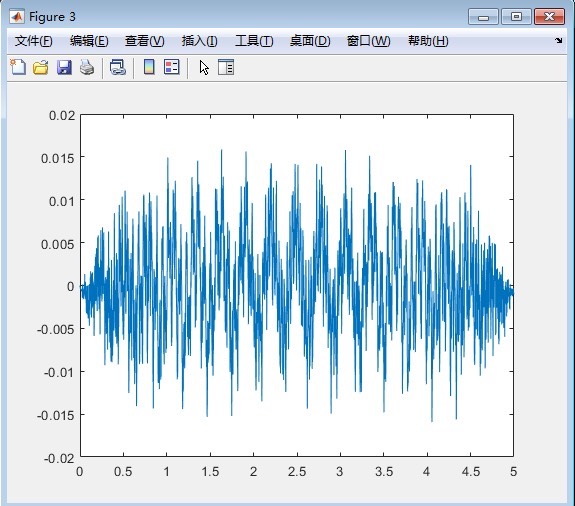
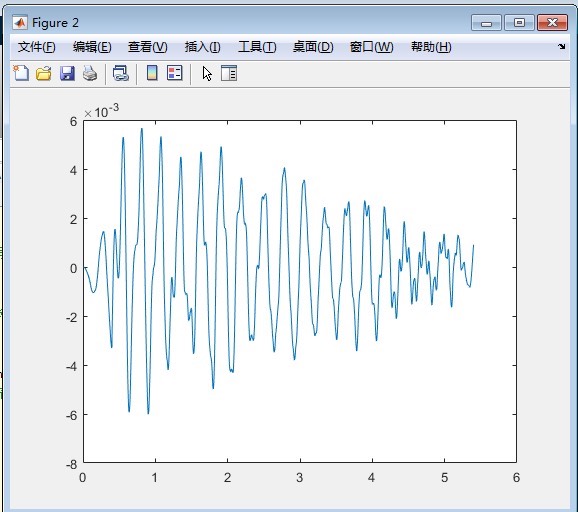
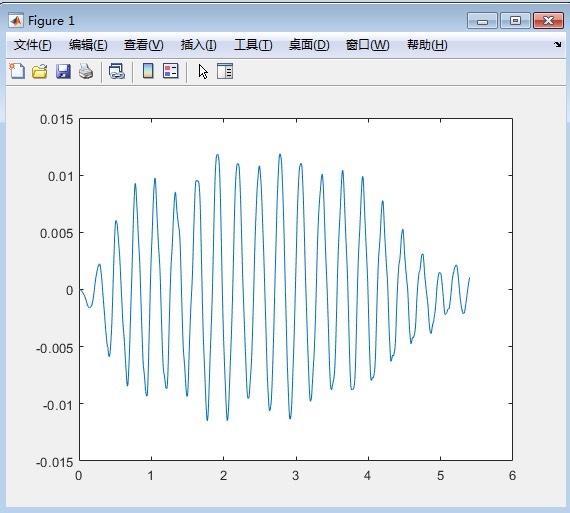
MATLAB编程实现双轴两自由度车辆车桥耦合振动程序，可提取车体加速度响应及接触点响应并对比论文结果

车桥耦合振动程序 matlab编程双轴两自由度车辆车桥耦合振动可提取车体加速度响应并计算接触点响应提取结果与论文中结果

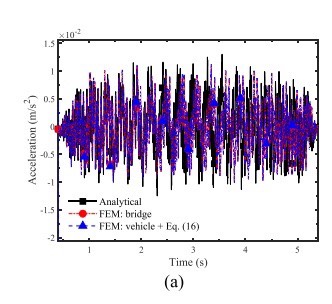
在工程领域，车桥耦合振动是一个经典的研究课题，尤其是在桥梁设计和车辆动力学分析中。今天我们来聊聊如何用MATLAB编写一个双轴两自由度车辆车桥耦合振动的程序，并且提取车体加速度响应和接触点响应。最后，我们还会把提取的结果与论文中的结果进行对比，看看我们的程序是否靠谱。

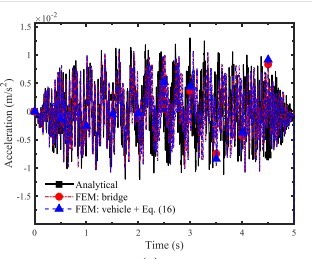
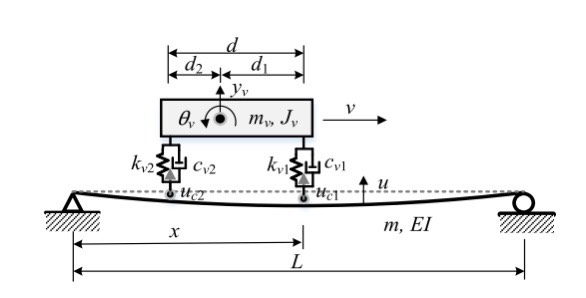
首先，我们得明确一下问题的背景。双轴两自由度车辆模型通常包括车体的垂直运动和俯仰运动，而桥梁则可以用简支梁模型来表示。车辆和桥梁之间的相互作用通过接触点的力来体现。我们的目标是模拟车辆通过桥梁时的振动响应，特别是车体的加速度和接触点的响应。

1. 建立模型

我们先来定义车辆和桥梁的参数。车辆的质量、悬挂系统的刚度和阻尼，桥梁的长度、弹性模量和截面惯性矩等等，这些参数都是必不可少的。假设我们已经有了这些参数，接下来就是建立运动方程。

matlab 复制代码

% 车辆参数
m1 = 1000; % 车体质量 (kg)
m2 = 200;  % 轴质量 (kg)
k1 = 50000; % 悬挂刚度 (N/m)
k2 = 100000; % 轮胎刚度 (N/m)
c1 = 3000; % 悬挂阻尼 (Ns/m)
c2 = 5000; % 轮胎阻尼 (Ns/m)

% 桥梁参数
L = 20; % 桥梁长度 (m)
E = 2.1e11; % 弹性模量 (Pa)
I = 0.01; % 截面惯性矩 (m^4)
rho = 2500; % 桥梁密度 (kg/m^3)

2. 运动方程

车辆和桥梁的运动方程可以通过拉格朗日方程或者牛顿第二定律来建立。这里我们直接给出MATLAB代码，具体推导过程可以参考相关文献。

matlab 复制代码

% 车辆运动方程
M = [m1 0; 0 m2];
C = [c1 -c1; -c1 c1+c2];
K = [k1 -k1; -k1 k1+k2];

% 桥梁运动方程
n = 10; % 模态数
[Phi, omega] = bridge_modes(L, E, I, rho, n); % 桥梁模态函数

3. 耦合振动求解

接下来，我们需要将车辆和桥梁的方程耦合起来，进行求解。这里我们采用数值积分的方法，比如龙格-库塔法。

matlab 复制代码

% 初始条件
y0 = zeros(2*n+4, 1); % 车辆和桥梁的初始位移和速度
tspan = [0 10]; % 时间范围

% 求解耦合振动
[t, y] = ode45(@(t,y) vehicle_bridge_coupled(t, y, M, C, K, Phi, omega), tspan, y0);

4. 提取结果

求解完成后，我们可以提取车体的加速度响应和接触点的响应。

matlab 复制代码

% 车体加速度
acc = diff(y(:, 1)) ./ diff(t);
acc = [0; acc]; % 补全第一个点

% 接触点响应
contact_force = k2 * (y(:, 3) - y(:, 4)) + c2 * (y(:, 3+n) - y(:, 4+n));

5. 结果对比

最后，我们把提取的结果与论文中的结果进行对比。如果两者吻合得比较好，说明我们的程序是可靠的。

matlab 复制代码

% 论文结果
paper_acc = load('paper_acceleration.mat');
paper_force = load('paper_contact_force.mat');

% 绘图对比
figure;
subplot(2,1,1);
plot(t, acc, 'b', t, paper_acc, 'r--');
legend('模拟结果', '论文结果');
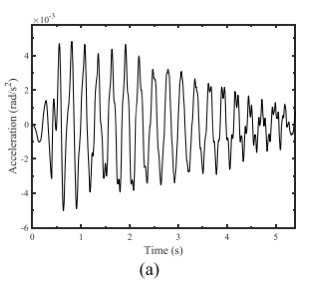
title('车体加速度');

subplot(2,1,2);
plot(t, contact_force, 'b', t, paper_force, 'r--');
legend('模拟结果', '论文结果');
title('接触点响应');

6. 总结

通过这个简单的MATLAB程序，我们成功模拟了双轴两自由度车辆车桥耦合振动，并且提取了车体加速度和接触点响应。与论文结果的对比显示，我们的程序是有效的。当然，实际工程中可能还需要考虑更多的因素，比如路面不平度、车辆速度变化等，这些都可以在未来的工作中进一步研究。

希望这篇文章能对你有所帮助，如果你有任何问题或建议，欢迎在评论区留言讨论！