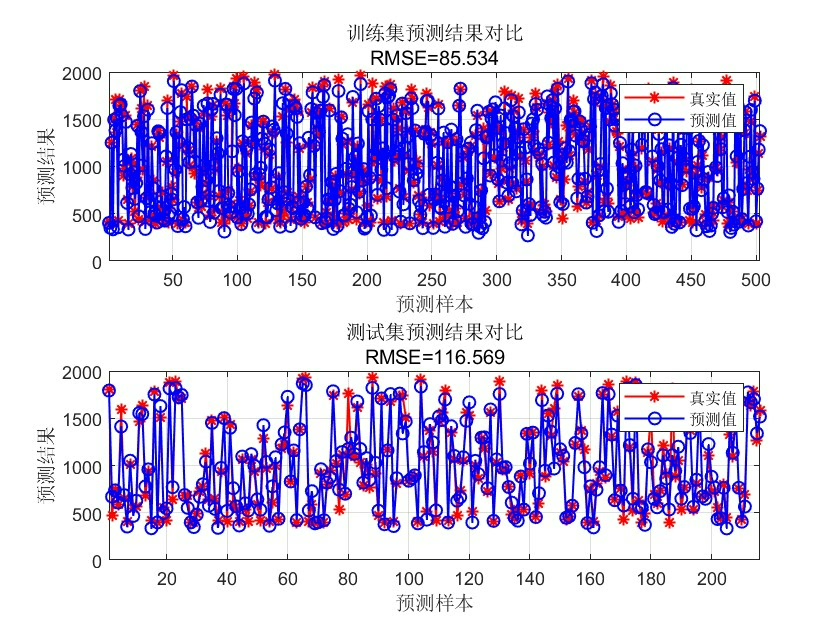
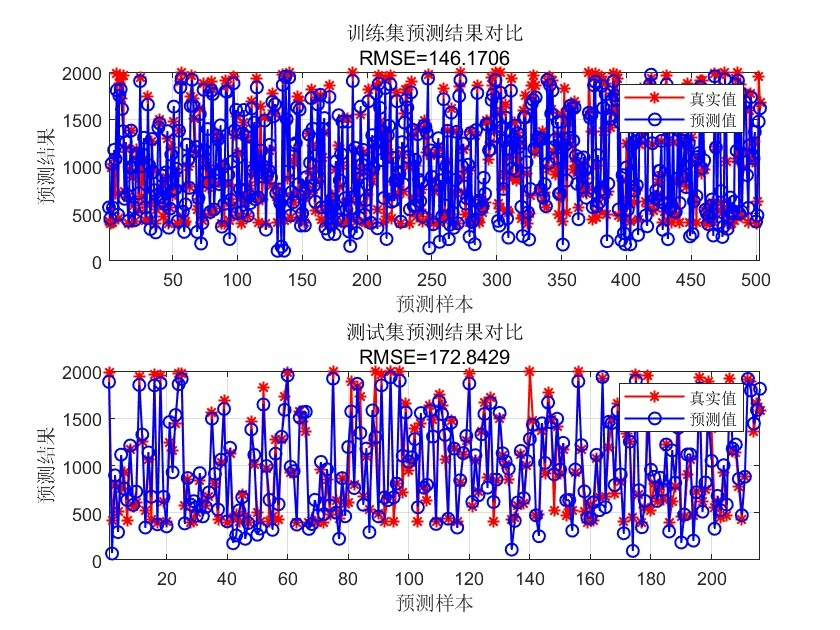
基于偏最小二乘算法（PLS）的多输出数据回归预测

基于偏最小二乘算法(PLS)的多输出数据回归预测PLS多输出数据回归 matlab代码注：暂无Matlab版本要求--推荐2018B版本及以上

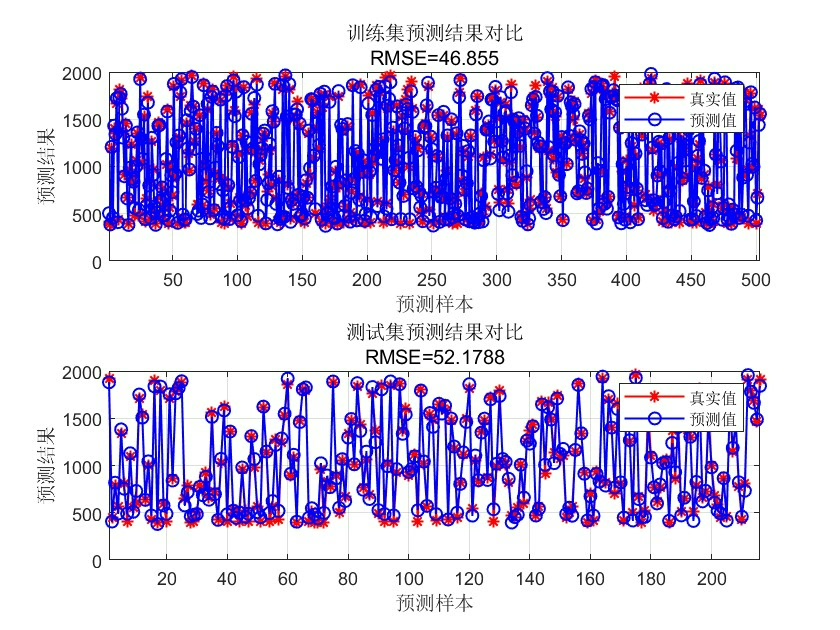
在数据处理和预测领域，偏最小二乘算法（PLS）是一种非常强大的工具，尤其适用于多输出数据回归预测。今天咱就来唠唠基于PLS的多输出数据回归以及对应的Matlab代码实现。

偏最小二乘算法（PLS）简介

PLS算法可以理解为是主成分分析（PCA）和多元线性回归（MLR）的结合体。它能够在处理自变量存在多重共线性的情况下，有效地进行回归建模。在多输出数据回归场景中，PLS可以同时对多个因变量进行建模预测，挖掘自变量和多个因变量之间的潜在关系。

Matlab代码实现

数据准备

假设我们有自变量矩阵 X 和因变量矩阵 Y，首先加载数据（这里以随机生成数据为例，实际应用中你需要加载真实数据）：

matlab 复制代码

% 随机生成自变量数据，100个样本，5个特征
X = randn(100, 5);
% 随机生成因变量数据，100个样本，3个输出
Y = randn(100, 3);

PLS回归建模

在Matlab中，我们可以使用 plsregress 函数来进行PLS回归建模。

matlab 复制代码

% 设定成分个数，这里假设为2
ncomp = 2;
[b, t, w, P, h, stats] = plsregress(X, Y, ncomp);

代码解释：

plsregress 函数返回多个结果。
b 是回归系数矩阵，它描述了自变量和因变量之间的线性关系。
t 是得分矩阵，它是由自变量矩阵 X 通过线性变换得到的，包含了数据的主要信息。
w 是权重矩阵，用于计算得分矩阵 t。
P 是载荷矩阵，描述了自变量与得分矩阵 t 之间的关系。
h 是预测残差误差矩阵。
stats 包含了模型的一些统计信息，比如 stats.R2 可以查看模型的决定系数，用于评估模型的拟合优度。

模型预测

建立好模型后，我们可以用它来进行预测。假设我们有新的自变量数据 Xnew：

matlab 复制代码

% 随机生成新的自变量数据，用于预测，20个样本，5个特征
Xnew = randn(20, 5);
Ypred = predict(b, t, P, Xnew);

这里 predict 函数利用之前得到的回归系数等信息，对新的数据 Xnew 进行预测，得到预测的因变量 Ypred。

总结

通过以上Matlab代码，我们完成了基于PLS算法的多输出数据回归预测的基本流程，从数据准备、建模到预测。PLS算法在处理多变量、多重共线性的数据时有着独特的优势，希望大家在实际项目中可以尝试应用它，挖掘数据背后的潜在规律。当然，实际应用中可能需要对模型进行更多的优化和评估，比如调整成分个数，观察不同评估指标来选择最优模型等。