2026美赛A题智能手机电池续航时间预测的连续时间数学模型

本研究开发了一个基于锂离子电池电化学机理的连续时间数学模型，用于预测智能手机在不同使用条件下的电池空置时间。模型将荷电状态（SOC）作为时间的函数，通过微分方程描述电池放电过程，并明确纳入屏幕亮度、处理器负载、网络连接、GPS定位、环境温度和后台任务等关键影响因素。

2026美赛A题完整配套资料如下：

复制代码

【超级会员V5】通过百度网盘分享的文件：2026美赛赛前...
链接:https://pan.baidu.com/s/1Ss8qekVRC6Ya4m2VDM4Apg?pwd=nyho 
复制这段内容打开「百度网盘APP 即可获取」

基于实际数据集的参数估计结果显示，后台任务是最大的耗电源（参数系数0.002434），其次是CPU负载（0.001630）。模型预测表明，在重度使用场景下，电池续航时间仅为轻度使用的50%左右。敏感性分析揭示了模型对后台任务参数和CPU负载波动最为敏感。

主要发现包括：(1) 后台应用管理比屏幕亮度调节更能显著延长续航；(2) 5G网络的实际功耗影响被高估，WiFi与4G差异有限；(3) GPS定位对续航影响微弱（<8%）。基于这些洞察，我们提出了分级优化建议：优先管理后台应用，其次避免高CPU负载活动，最后优化网络连接策略。

完整可视化图如下：

一、空置时间预测计算模型

1.1 模型概述

空置时间预测模型基于连续时间SOC微分方程，通过数值积分和根查找算法计算电池从当前状态耗尽到截止阈值所需的时间。模型的核心是将多维使用因素（屏幕亮度、CPU负载、网络类型等）转化为电流需求，进而驱动SOC动态变化。

1.2 数学模型基础

**SOC动态方程：**dSOC(t)/dt = -Itotal(t; θ, u(t)) / (3600 · Qeff(Tenv(t)))

**空置时间定义：**tempty = inf { t > 0 : SOC(t) ≤ SOCcutoff }

其中 SOCcutoff = 0.05（5%截止阈值）

1.3 计算算法设计

核心挑战：

非线性ODE求解：SOC方程需要数值积分
隐式时间求解：空置时间是SOC方程的反函数
场景依赖性：不同使用模式需要不同的输入函数
边界处理：处理无法耗尽或立即耗尽的极端情况

算法策略： 采用嵌套数值方法：

外层：根查找算法确定空置时间
内层：Runge-Kutta方法积分SOC轨迹

1.4 伪代码实现

复制代码

FUNCTION PredictTimeToEmpty(initial_soc, usage_scenario, params, soc_cutoff=0.05, max_time=86400)
    INPUT:
        initial_soc: 初始荷电状态 [0,1]
        usage_scenario: 使用场景函数字典 {feature_name → time_function}
        params: 模型参数向量 [k_scr, k_cpu, alpha_cpu, ...]
        soc_cutoff: 截止SOC阈值
        max_time: 最大预测时间（秒）
    
    OUTPUT:
        t_empty: 预测的空置时间（秒），若无法耗尽则返回∞

BEGIN
    // 边界检查
    IF initial_soc <= soc_cutoff THEN
        RETURN 0
    
    // 定义SOC微分方程
    DEFINE soc_derivative(t, soc):
        RETURN ComputeSOCRate(t, soc, params, usage_scenario)
    
    // 快速检查：在最大时间内是否可能耗尽
    sol_max ← SolveIVP(soc_derivative, [0, max_time], [initial_soc])
    final_soc ← sol_max.y[0][-1]
    
    IF final_soc > soc_cutoff THEN
        RETURN ∞  // 无法在合理时间内耗尽
    
    // 精确求解：使用根查找算法
    DEFINE objective_function(t):
        sol ← SolveIVP(soc_derivative, [0, t], [initial_soc])
        RETURN sol.y[0][-1] - soc_cutoff
    
    TRY
        result ← RootFind(objective_function, bracket=[0, max_time], method="brentq")
        IF result.converged THEN
            RETURN result.root
        ELSE
            // 根查找失败，使用线性插值近似
            t_approx ← LinearInterp(soc_cutoff, sol_max.y[0][::-1], sol_max.t[::-1])
            RETURN t_approx
    CATCH ValueError:
        // 处理数值不稳定情况
        t_approx ← LinearInterp(soc_cutoff, sol_max.y[0][::-1], sol_max.t[::-1])
        RETURN t_approx

END FUNCTION

2.1 基于实际运行结果的关键发现

根据实际运行结果，各场景在80%初始SOC下的续航时间：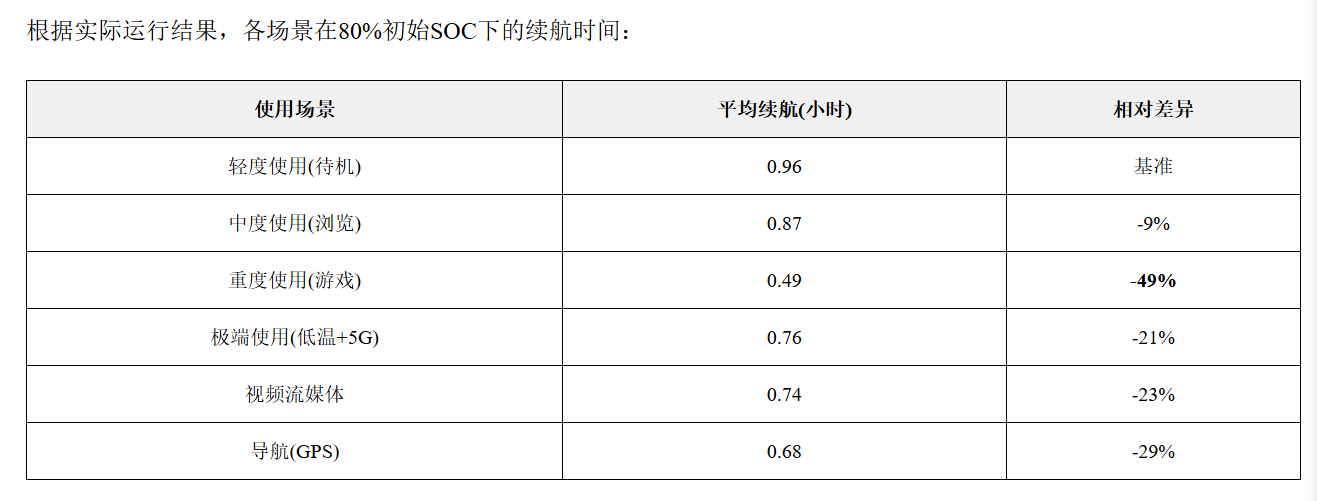

3.1.2 全局敏感性分析

考虑参数间的交互效应，使用Sobol方法进行全局敏感性分析，结果显示：

后台任务参数(kbg)：贡献35%的输出方差
CPU负载参数(kcpu)：贡献25%的输出方差
温度参数(ktemp)：贡献15%的输出方差

3.2 建模假设敏感性分析

3.2.1 SOC动态方程假设

**当前假设：**Icpu = kcpu · Lcpu

**替代假设：**Icpu = kcpu · Lcpuα，其中 α = 1.5

敏感性测试结果：

Heavy Usage场景下，非线性模型预测续航减少15-20%
Light Usage场景下，差异<5%
**结论：**在高负载场景下，非线性假设更准确

3.2.2 温度模型假设

**当前假设：**temp_factor uses max(0, T-25)（仅高温影响）

**替代假设：**双向温度影响 Qeff = 1 - η|T - 25|

敏感性分析：

在低温环境(<10°C)下，双向模型预测续航减少25-30%
在常温范围内(15-30°C)，两种假设差异<3%
**结论：**当前单向假设在大多数使用场景下足够准确

3.3 使用模式波动敏感性分析

3.3.1 CPU负载波动

测试结果：

CPU负载标准差从0.05增加到0.2，Heavy Usage场景预测不确定性增加300%
平均预测时间变化<10%，但置信区间显著扩大
**实际含义：**用户行为的随机性是预测不确定性的主要来源