目录
[1. 什么是扫频信号？](#1. 什么是扫频信号？)
[2. 直观理解：与普通正弦波的区别](#2. 直观理解：与普通正弦波的区别)
[3. 常见分类](#3. 常见分类)
[4. 核心作用：为什么要用扫频信号？](#4. 核心作用：为什么要用扫频信号？)
[5. 项目实战分析 (结合 FPGA/C++ 代码)](#5. 项目实战分析 (结合 FPGA/C++ 代码))
[6. 总结](#6. 总结)
前言
本文旨在记录扫频信号（Chirp）的时频特性，为后续基于扫频法的AD芯片性能测试与数据分析提供理论参考。
1. 什么是扫频信号？
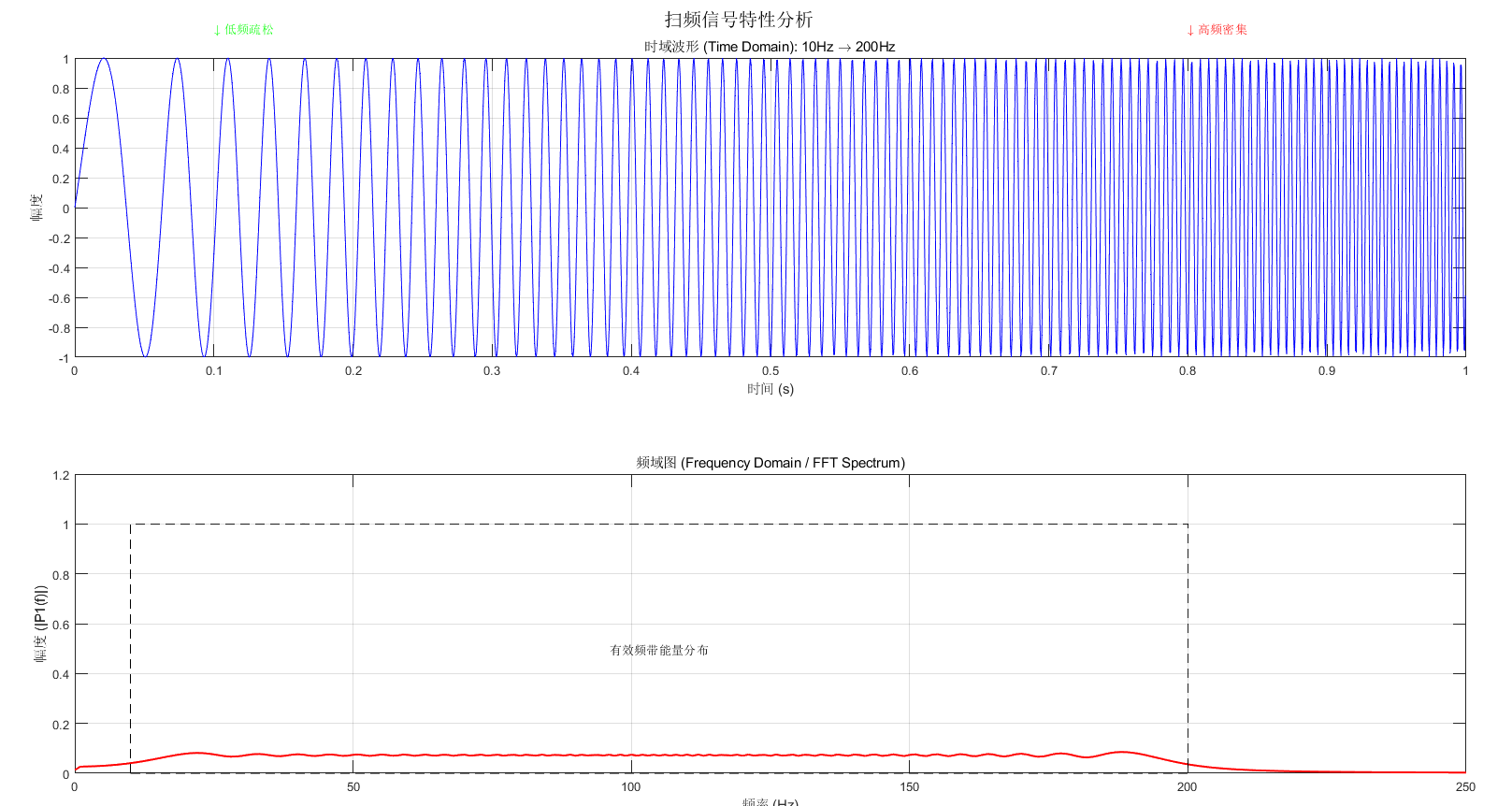
定义：
扫频信号（Sweep Signal），又称为 Chirp 信号（线性调频信号）。它的核心特征是频率随时间有规律地变化。
听觉类比：
它的音调不是固定的，而是像警报声、雷达声或鸟鸣声一样，从低音平滑过渡到高音（上扫频），或者反之（下扫频）。
示例代码：
Matlab
%% 扫频信号生成与分析脚本
% 功能：生成线性扫频信号，并绘制时域波形和频域频谱
% 作者：lhw
% 日期：2026-01-16
clc; clear; close all;
%% 1. 参数设置
fs = 2000; % 采样率 (Hz)，设高一点以便观察频谱
T = 1.0; % 信号持续时间 (秒)
f_start = 10; % 起始频率 10Hz
f_end = 200; % 终止频率 200Hz
%% 2. 信号生成
t = 0 : 1/fs : T - 1/fs; % 时间轴
% 线性扫频信号公式:
% 瞬时频率 f(t) = f_start + k * t
% 相位 phi(t) = 2 * pi * 积分(f(t)) = 2 * pi * (f_start * t + 0.5 * k * t^2)
k = (f_end - f_start) / T; % 频率变化率 (Hz/s)
phase = 2 * pi * (f_start * t + 0.5 * k * t.^2); %相位等于瞬时频率的积分
signal = sin(phase); % 生成正弦扫频信号
%% 3. 频域分析 (FFT)
N = length(signal); % 采样点数
f = (0 : N-1) * (fs / N); % 频率轴 (0 到 fs)
Y = fft(signal); % 快速傅里叶变换
P2 = abs(Y / N); % 双边频谱幅度
P1 = P2(1 : floor(N/2)+1); % 取单边频谱
P1(2:end-1) = 2 * P1(2:end-1); % 幅度修正
f_axis = f(1 : floor(N/2)+1); % 单边频率轴
%% 4. 绘图
figure('Color', 'w', 'Name', '扫频信号分析');
% --- 子图 1: 时域波形 ---
subplot(2, 1, 1);
plot(t, signal, 'b', 'LineWidth', 1);
title(['时域波形 (Time Domain): ', num2str(f_start), 'Hz \rightarrow ', num2str(f_end), 'Hz']);
xlabel('时间 (s)');
ylabel('幅度');
grid on;
xlim([0, T]);
% 局部放大提示（可选）
text(0.1, 1.2, '\downarrow 低频疏松', 'Color', 'g', 'FontSize', 10);
text(0.8, 1.2, '\downarrow 高频密集', 'Color', 'r', 'FontSize', 10);
% --- 子图 2: 频域图 (FFT 频谱) ---
subplot(2, 1, 2);
plot(f_axis, P1, 'r', 'LineWidth', 1.5);
title('频域图 (Frequency Domain / FFT Spectrum)');
xlabel('频率 (Hz)');
ylabel('幅度 (|P1(f)|)');
grid on;
xlim([0, f_end + 50]); % X轴范围显示到终止频率稍微多一点的地方
ylim([0, 1.2]);
% 添加标注：展示频谱的平坦特性
rectangle('Position', [f_start, 0, f_end-f_start, 1], 'EdgeColor', 'k', 'LineStyle', '--');
text((f_start+f_end)/2, 0.5, '有效频带能量分布', 'HorizontalAlignment', 'center');
% 调整布局
sgtitle('扫频信号特性分析');2. 直观理解：与普通正弦波的区别
| 信号类型 | 频率特征 | 波形外观 |
|---|---|---|
| 普通正弦波 | 恒定 | 波峰与波峰之间的距离（周期）始终保持不变。 |
| 扫频信号 | 变化 | 起始段（低频）：波形稀疏，波浪很宽，波峰间距大。 后段（高频）：波形密集，波浪紧凑，波峰间距极小。 |
3. 常见分类
根据频率变化的规律，主要分为两类：
-
线性扫频 (Linear Sweep)
-
规律： 频率随时间匀速增加。
-
示例： 第1秒 10Hz
第2秒 20Hz
-
应用： 通用的频响测试、雷达脉冲压缩。（注：本项目中使用的是此类）
-
-
对数扫频 (Logarithmic Sweep)
-
规律： 频率随时间成倍增加。
-
示例： 10Hz \\rightarrow 100Hz \\rightarrow 1000Hz...
-
应用： 音频设备测试（因为人耳对频率的感知是非线性的，呈对数关系）。
-
4. 核心作用：为什么要用扫频信号？
在工程中，生成扫频信号的主要目的是为了进行 系统辨识 (System Identification) 或 频率响应测试。
场景假设： 测试采集板（ADC前端电路）的滤波特性。
-
❌ 笨办法（单点测试）：
-
手动输入 10Hz
-
手动输入 100Hz
-
... 重复无数次。
-
缺点：效率极低，容易漏掉中间的频率点。
-
-
✅ 聪明办法（扫频测试）：
-
操作： 输入一个从
-
原理： 这个信号在时域上虽然只是一段波形，但在频域上包含了该范围内的所有频率成分。
-
结果分析： 将采集到的波形进行 FFT 分析。如果发现高频部分的幅度明显衰减，即可直接得出电路的"幅频特性曲线"（Bode 图）。
-
优点：一次采集，全频段分析。
-
5. 项目实战分析 (结合 FPGA/C++ 代码)
基于现有的 C++ 与 FPGA 代码逻辑，本项目中的应用如下：
-
工作模式：
-
Mode = 4: 方波线性扫频（10Hz ~ 1MHz）。 -
Mode = 5: 正弦波线性扫频（DDS产生，10Hz ~ 1MHz）。
-
-
关键参数定义：
-
-
-
- 代码逻辑：
- 代码逻辑：
-
6. 总结
扫频信号本质上是一把"频率的尺子"。通过发送这把"尺子"穿过硬件系统，可以一次性测量出系统在各个频率刻度下的性能表现（如增益、衰减、相移等）。