【通信原理】数字基带传输系统（二）——数字基带信号码间干扰均衡技术部分响应技术（笔记总结）

第5章数字基带传输系统学习笔记

文章目录

[第5章数字基带传输系统学习笔记](#第5章数字基带传输系统学习笔记)
- [5. 无码间干扰基带传输系统的抗噪声性能](#5. 无码间干扰基带传输系统的抗噪声性能)
- - [5.1 分析模型](#5.1 分析模型)
  - [5.2 双极性信号的抗噪声性能](#5.2 双极性信号的抗噪声性能)
  - [5.3 单极性信号的抗噪声性能](#5.3 单极性信号的抗噪声性能)
  - [5.4 性能对比](#5.4 性能对比)
- [6. 眼图](#6. 眼图)
- [7. 均衡技术](#7. 均衡技术)
- - [7.1 均衡的目的](#7.1 均衡的目的)
  - [7.2 均衡方法分类](#7.2 均衡方法分类)
  - [7.3 时域均衡原理](#7.3 时域均衡原理)
  - - 横向滤波器结构
    - 有限长横向滤波器
  - [7.4 均衡效果衡量准则](#7.4 均衡效果衡量准则)
  - [7.5 迫零均衡算法（ZF）](#7.5 迫零均衡算法（ZF）)
- [8. 部分响应技术](#8. 部分响应技术)
- - [8.1 设计目标](#8.1 设计目标)
  - [8.2 设计思想](#8.2 设计思想)
  - [8.3 第I类部分响应系统](#8.3 第I类部分响应系统)
  - [8.4 第IV类部分响应系统](#8.4 第IV类部分响应系统)
  - [8.5 部分响应的一般形式](#8.5 部分响应的一般形式)
  - [8.4 第IV类部分响应系统](#8.4 第IV类部分响应系统)
  - [8.5 部分响应的一般形式](#8.5 部分响应的一般形式)

5. 无码间干扰基带传输系统的抗噪声性能

前面在不考虑噪声影响时，讨论了无码间串扰的基带传输特性。本节将研究在无码间串扰条件下，由信道噪声引起的误码率。

5.1 分析模型

将发送滤波器和信道简略，只从信道端的输出开始考虑，简化分析模型：

假设加性噪声 n ( t ) n(t) n(t)为零均值高斯白噪声。

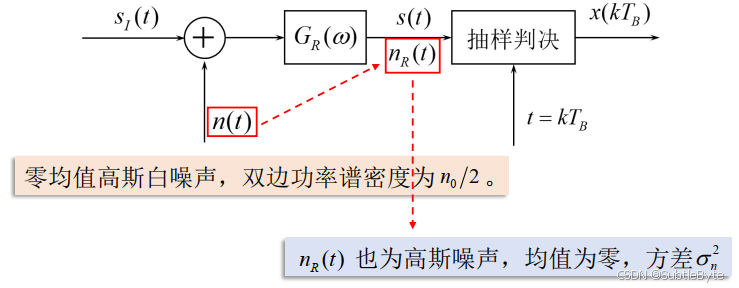
在无ISI条件下，抽样时刻的输出为：
x ( k T B + t 0 ) = a k h ( t 0 ) + n R ( k T B + t 0 ) x\left(k T_{B}+t_{0}\right)=a_{k} h\left(t_{0}\right)+n_{R}\left(k T_{B}+t_{0}\right) x(kTB+t0)=akh(t0)+nR(kTB+t0)

x ( k T B + t 0 ) = a k h ( t 0 ) + ∑ n ≠ k a n h [ ( k − n ) T B + t 0 ] + n R ( k T B + t 0 ) ⇓ I S I = ∑ n ≠ k a n h [ ( k − n ) T B + t 0 ] = 0 x ( k T B + t 0 ) = a k h ( t 0 ) + n R ( k T B + t 0 ) \begin{array}{c} x\left(k T_{B}+t_{0}\right)=a_{k} h\left(t_{0}\right)+\sum_{n \neq k} a_{n} h\left[(k-n) T_{B}+t_{0}\right]+n_{R}\left(k T_{B}+t_{0}\right) \\ \Downarrow \mathrm{ISI}=\sum_{n \neq k} a_{n} h\left[(k-n) T_{B}+t_{0}\right]=0 \\ x\left(k T_{B}+t_{0}\right)=a_{k} h\left(t_{0}\right)+n_{R}\left(k T_{B}+t_{0}\right) \end{array} x(kTB+t0)=akh(t0)+∑n=kanh[(k−n)TB+t0]+nR(kTB+t0)⇓ISI=∑n=kanh[(k−n)TB+t0]=0x(kTB+t0)=akh(t0)+nR(kTB+t0)

其中，由于接收滤波器又是一个线性网络，所以 n R ( t ) n_R(t) nR(t)也是零均值高斯噪声

它的功率谱密度为：

P n ( f ) = n 0 2 ∣ G R ( f ) ∣ 2 P_{n}(f)=\frac{n_{0}}{2}\left|G_{\mathrm{R}}(f)\right|^{2} Pn(f)=2n0∣GR(f)∣2

方差（噪声平均功率）为：

σ n 2 = ∫ − ∞ ∞ n 0 2 ∣ G R ( f ) ∣ 2 d f \sigma_{n}^{2}=\int_{-\infty}^{\infty} \frac{n_{0}}{2}\left|G_{\mathrm{R}}(f)\right|^{2} \mathrm{~d} f σn2=∫−∞∞2n0∣GR(f)∣2 df

一维概率密度函数为：

f ( V ) = 1 2 π σ n e − V 2 / 2 σ n 2 f(V)=\frac{1}{\sqrt{2 \pi} \sigma_{n}} \mathrm{e}^{-V^{2} / 2 \sigma_{n}^{2}} f(V)=2π σn1e−V2/2σn2

5.2 双极性信号的抗噪声性能

信号模型

x ( k T B ) = { A + n R ( k T B ) 发"1" − A + n R ( k T B ) 发"0" x(kT_B) = \begin{cases} A + n_R(kT_B) & \text{发"1"} \\ -A + n_R(kT_B) & \text{发"0"} \end{cases} x(kTB)={A+nR(kTB)−A+nR(kTB)发"1"发"0"

我们可以得到

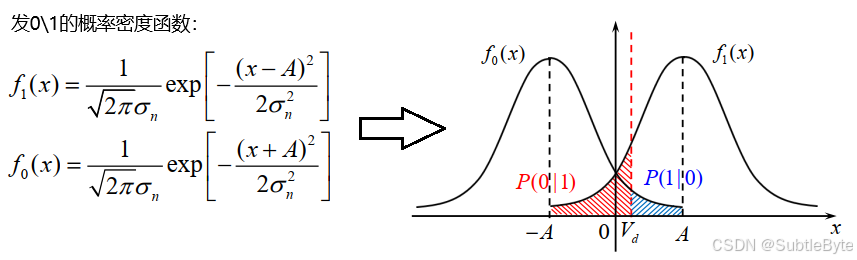
判决规则

设有一判决门限 V d V_d Vd
{ x ( k T B ) > V d 判"1" x ( k T B ) < V d 判"0" \begin{cases} x(kT_B) > V_d & \text{判"1"} \\ x(kT_B) < V_d & \text{判"0"} \end{cases} {x(kTB)>Vdx(kTB)<Vd判"1"判"0"

误码率分析

发1判0的概率：
P ( 0 ∣ 1 ) = ∫ − ∞ V d f 1 ( x ) d x = 1 2 + 1 2 erf ( V d − A 2 σ n ) P(0|1) = \int_{-\infty}^{V_d} f_1(x) dx = \frac{1}{2} + \frac{1}{2} \text{erf}\left( \frac{V_d - A}{\sqrt{2}\sigma_n} \right) P(0∣1)=∫−∞Vdf1(x)dx=21+21erf(2 σnVd−A)
发0判1的概率：
P ( 1 ∣ 0 ) = ∫ V d + ∞ f 0 ( x ) d x = 1 2 − 1 2 erf ( V d + A 2 σ n ) P(1|0) = \int_{V_d}^{+\infty} f_0(x) dx = \frac{1}{2} - \frac{1}{2} \text{erf}\left( \frac{V_d + A}{\sqrt{2}\sigma_n} \right) P(1∣0)=∫Vd+∞f0(x)dx=21−21erf(2 σnVd+A)
总误码率：

P e = P ( 1 ) P ( 0 ∣ 1 ) + P ( 0 ) P ( 1 ∣ 0 ) = P ( 1 ) [ 1 2 + 1 2 erf ⁡ ( V d − A 2 σ n ) ] + P ( 0 ) [ 1 2 − 1 2 erf ⁡ ( V d + A 2 σ n ) ] P_{e}=P(1) P(0 \mid 1)+P(0) P(1 \mid 0)=P(1)\left[\frac{1}{2}+\frac{1}{2} \operatorname{erf}\left(\frac{V_{d}-A}{\sqrt{2} \sigma_{n}}\right)\right]+P(0)\left[\frac{1}{2}-\frac{1}{2} \operatorname{erf}\left(\frac{V_{d}+A}{\sqrt{2} \sigma_{n}}\right)\right] Pe=P(1)P(0∣1)+P(0)P(1∣0)=P(1)[21+21erf(2 σnVd−A)]+P(0)[21−21erf(2 σnVd+A)]

最佳判决门限

V d ∗ = σ n 2 2 A ln ⁡ P ( 0 ) P ( 1 ) V_d^* = \frac{\sigma_n^2}{2A} \ln \frac{P(0)}{P(1)} Vd∗=2Aσn2lnP(1)P(0)

推导：

已知： P e = P ( 1 ) ⋅ ∫ − ∞ V d f 1 ( x ) d x + P ( 0 ) ⋅ ∫ V d + ∞ f 0 ( x ) d x P_{e} =P(1) \cdot \int_{-\infty}^{V_{d}} f_{1}(x) \mathrm{d} x+P(0) \cdot \int_{V_{d}}^{+\infty} f_{0}(x) \mathrm{d} x Pe=P(1)⋅∫−∞Vdf1(x)dx+P(0)⋅∫Vd+∞f0(x)dx当 P ( 1 ) P(1) P(1)、 P ( 0 ) P(0) P(0)、 f 1 ( x ) f_1(x) f1(x)、 f 0 ( x ) f_0(x) f0(x)已知的情况下 P e P_e Pe是一个关于 V d V_d Vd的式子。求 P e P_e Pe关于 V d V_d Vd的偏导，令其为0，即可求解。
∂ P e ∂ V d = 0 P ( 1 ) f 1 ( V d ∗ ) − P ( 0 ) f 0 ( V d ∗ ) = 0 \frac{\partial P_{e}}{\partial V_{d}}=0 \quad P(1) f_{1}\left(V_{d}^{*}\right)-P(0) f_{0}\left(V_{d}^{*}\right)=0 ∂Vd∂Pe=0P(1)f1(Vd∗)−P(0)f0(Vd∗)=0

特殊情况：等概时（ P ( 0 ) = P ( 1 ) = 1 / 2 P(0)=P(1)=1/2 P(0)=P(1)=1/2）： V d ∗ = 0 V_d^* = 0 Vd∗=0

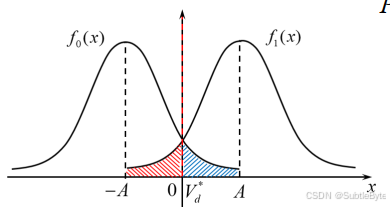
此时的总误码率为：
P e = 1 2 erfc ( A 2 σ n ) P_e = \frac{1}{2} \text{erfc}\left( \frac{A}{\sqrt{2}\sigma_n} \right) Pe=21erfc(2 σnA)

5.3 单极性信号的抗噪声性能

信号模型

x ( k T B ) = { A + n R ( k T B ) 发"1" n R ( k T B ) 发"0" x(kT_B) = \begin{cases} A + n_R(kT_B) & \text{发"1"} \\ n_R(kT_B) & \text{发"0"} \end{cases} x(kTB)={A+nR(kTB)nR(kTB)发"1"发"0"

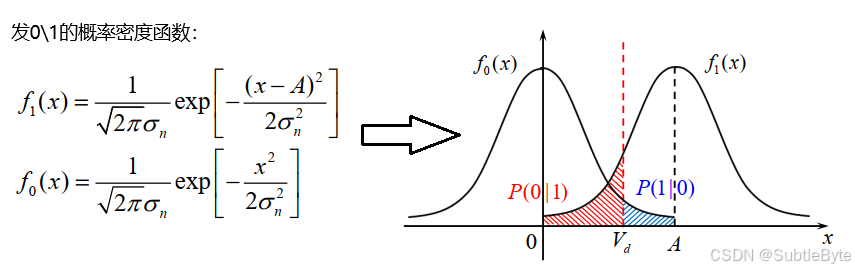
误码率分析

发1判0的概率：
P ( 0 ∣ 1 ) = 1 2 + 1 2 erf ( V d − A 2 σ n ) P(0|1) = \frac{1}{2} + \frac{1}{2} \text{erf}\left( \frac{V_d - A}{\sqrt{2}\sigma_n} \right) P(0∣1)=21+21erf(2 σnVd−A)
发0判1的概率：
P ( 1 ∣ 0 ) = 1 2 − 1 2 erf ( V d 2 σ n ) P(1|0) = \frac{1}{2} - \frac{1}{2} \text{erf}\left( \frac{V_d}{\sqrt{2}\sigma_n} \right) P(1∣0)=21−21erf(2 σnVd)

最佳判决门限

V d ∗ = A 2 + σ n 2 A ln ⁡ P ( 0 ) P ( 1 ) V_d^* = \frac{A}{2} + \frac{\sigma_n^2}{A} \ln \frac{P(0)}{P(1)} Vd∗=2A+Aσn2lnP(1)P(0)

等概时： V d ∗ = A / 2 V_d^* = A/2 Vd∗=A/2

总误码率（等概时）
P e = 1 2 erfc ( A 2 2 σ n ) P_e = \frac{1}{2} \text{erfc}\left( \frac{A}{2\sqrt{2}\sigma_n} \right) Pe=21erfc(22 σnA)

5.4 性能对比

比较项目	双极性信号	单极性信号
数学表达式	x ( k T B ) = { A + n R ( k T B ) 发"1" − A + n R ( k T B ) 发"0" x(kT_B) = \begin{cases} A + n_R(kT_B) & \text{发"1"} \\ -A + n_R(kT_B) & \text{发"0"} \end{cases} x(kTB)={A+nR(kTB)−A+nR(kTB)发"1"发"0"	x ( k T B ) = { A + n R ( k T B ) 发"1" n R ( k T B ) 发"0" x(kT_B) = \begin{cases} A + n_R(kT_B) & \text{发"1"} \\ n_R(kT_B) & \text{发"0"} \end{cases} x(kTB)={A+nR(kTB)nR(kTB)发"1"发"0"
最佳判决门限	V d ∗ = σ n 2 2 A ln ⁡ P ( 0 ) P ( 1 ) V_d^* = \frac{\sigma_n^2}{2A} \ln \frac{P(0)}{P(1)} Vd∗=2Aσn2lnP(1)P(0)	V d ∗ = A 2 + σ n 2 A ln ⁡ P ( 0 ) P ( 1 ) V_d^* = \frac{A}{2} + \frac{\sigma_n^2}{A} \ln \frac{P(0)}{P(1)} Vd∗=2A+Aσn2lnP(1)P(0)
等概时门限	V d ∗ = 0 V_d^* = 0 Vd∗=0	V d ∗ = A 2 V_d^* = \frac{A}{2} Vd∗=2A
误码率（发"1"判"0"）	$$P(0	1) = \frac{1}{2} + \frac{1}{2} \text{erf}\left( \frac{V_d - A}{\sqrt{2}\sigma_n} \right)$$
误码率（发"0"判"1"）	$$P(1	0) = \frac{1}{2} - \frac{1}{2} \text{erf}\left( \frac{V_d + A}{\sqrt{2}\sigma_n} \right)$$
总误码率（一般情况）	P e = P ( 1 ) [ 1 2 + 1 2 erf ⁡ ( V d − A 2 σ n ) ] + P ( 0 ) [ 1 2 − 1 2 erf ⁡ ( V d + A 2 σ n ) ] P_e = P(1)\left[\frac{1}{2}+\frac{1}{2} \operatorname{erf}\left(\frac{V_{d}-A}{\sqrt{2} \sigma_{n}}\right)\right]+P(0)\left[\frac{1}{2}-\frac{1}{2} \operatorname{erf}\left(\frac{V_{d}+A}{\sqrt{2} \sigma_{n}}\right)\right] Pe=P(1)[21+21erf(2 σnVd−A)]+P(0)[21−21erf(2 σnVd+A)]	P e = P ( 1 ) [ 1 2 + 1 2 erf ⁡ ( V d − A 2 σ n ) ] + P ( 0 ) [ 1 2 − 1 2 erf ⁡ ( V d 2 σ n ) ] P_e = P(1)\left[\frac{1}{2}+\frac{1}{2} \operatorname{erf}\left(\frac{V_{d}-A}{\sqrt{2} \sigma_{n}}\right)\right]+P(0)\left[\frac{1}{2}-\frac{1}{2} \operatorname{erf}\left(\frac{V_{d}}{\sqrt{2} \sigma_{n}}\right)\right] Pe=P(1)[21+21erf(2 σnVd−A)]+P(0)[21−21erf(2 σnVd)]
总误码率（等概情况）	P e = 1 2 erfc ( A 2 σ n ) P_e = \frac{1}{2} \text{erfc}\left( \frac{A}{\sqrt{2}\sigma_n} \right) Pe=21erfc(2 σnA)	P e = 1 2 erfc ( A 2 2 σ n ) P_e = \frac{1}{2} \text{erfc}\left( \frac{A}{2\sqrt{2}\sigma_n} \right) Pe=21erfc(22 σnA)
直流分量	无直流分量	有直流分量

相同 A / σ n A/\sigma_n A/σn：双极性系统的误码率低于单极性系统

直观理解：双极性信号噪声容限更大，故抗噪声性能更强
当符号先验等概时，单极性信号的最佳判决门限会随着信道特性变化而变化；双极性信号的最佳判决门限不随信道特性变化
抗噪声性能：双极性优于单极性（噪声容限更大）

6. 眼图

眼图的概念

将接收滤波器的输出信号连接到示波器的垂直输入端，同时调整水平扫描周期为码元周期 T B T_B TB，在示波器上显示的图形称为眼图。
眼图的作用
- 定性估计系统性能优劣
- 反映码间干扰和噪声的强弱
- 指导接收滤波器的调整
眼图的特征参数

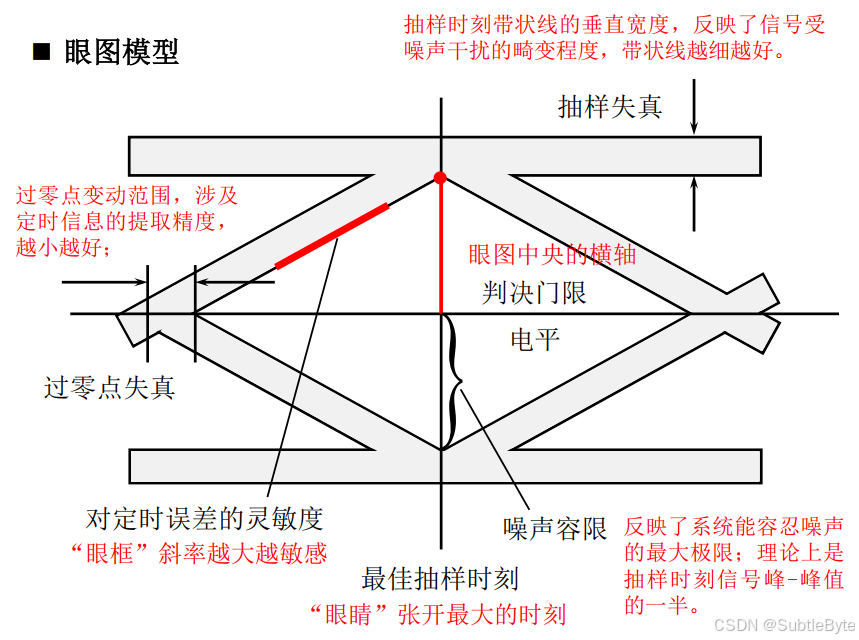
最佳抽样时刻：眼睛张开最大的时刻
判决门限：眼图中央的横轴位置
噪声容限：抽样时刻信号峰-峰值的一半
抽样失真：抽样时刻迹线的垂直宽度（反映噪声影响）
过零点失真：过零点变动范围（影响定时提取精度）
对定时误差的灵敏度："眼框"斜率越大，对定时误差越敏感

眼图与信号类型的关系
- 二进制双极性波形：一个码元周期内看到一只眼睛
- M进制双极性波形 ：一个码元周期内看到 ( M − 1 ) (M-1) (M−1) 只眼睛
- AMI码或HDB₃码：三电平，眼图中间有代表连0的水平线
- 扫描周期为 n T B nT_B nTB ：看到并排的 n n n 只眼睛
最佳眼图特征
- "眼睛"张开大且端正 → ISI小
- 迹线清晰 → 噪声小
- 总结：单眼皮大眼睛------最佳眼图

7. 均衡技术

这是一种改善系统性能的措施

7.1 均衡的目的

减小或消除码间干扰（ISI），校正系统传输特性。

均衡的目的是为了减小码间干扰。因为数字基带系统由三部分组成：发滤波器、信道和收滤波器。信道特性的变化以及收发滤波器的设计不良，都使得整个系统的传输特性很难直接满足无码间干扰条件。因此，我们需要一种方法使系统经过处理后满足无码间干扰条件。均衡的思想就是在基带系统和抽样判决器之间串联一个均衡器。

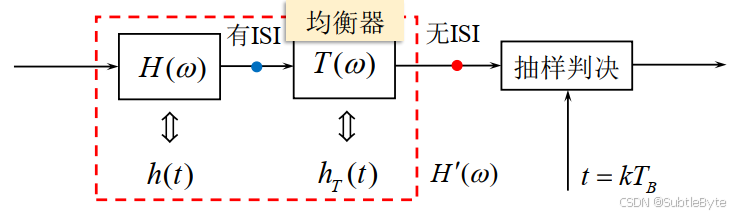
在基带系统和抽样判决器之间级联均衡器。均衡器为可调或不可调的滤波器，用于校正或补偿系统特性，减小码间干扰

7.2 均衡方法分类

频域均衡

通过频率校正使均衡后系统特性满足奈奎斯特第一准则：
H ( ω ) ⋅ T ( ω ) = H ′ ( ω ) H(\omega) \cdot T(\omega) = H'(\omega) H(ω)⋅T(ω)=H′(ω)

满足：
∑ i H ′ ( ω + 2 π i T B ) = T B ∣ ω ∣ ≤ π T B \sum_i H'\left( \omega + \frac{2\pi i}{T_B} \right) = T_B \quad |\omega| \leq \frac{\pi}{T_B} i∑H′(ω+TB2πi)=TB∣ω∣≤TBπ
时域均衡

使有码间干扰的冲激响应波形 h ( t ) h(t) h(t)变换后无码间干扰:
h ( t ) ∗ h T ( t ) = h ′ ( t ) h(t) * h_T(t) = h'(t) h(t)∗hT(t)=h′(t)

其中：
h ′ ( k T B ) = { 1 k = 0 0 k ≠ 0 h'(kT_B) = \begin{cases} 1 & k=0 \\ 0 & k\neq 0 \end{cases} h′(kTB)={10k=0k=0

7.3 时域均衡原理

横向滤波器结构

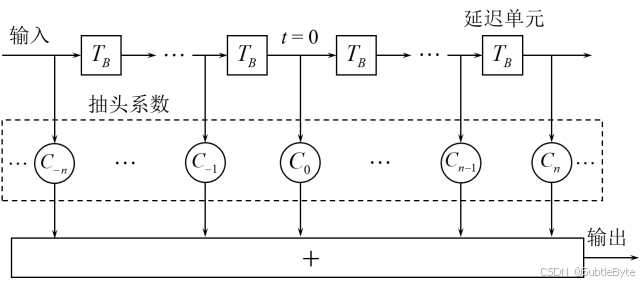
时域均衡器通常采用横向滤波器实现，其冲击响应为：
h T ( t ) = ∑ n = − ∞ + ∞ C n δ ( t − n T B ) h_T(t) = \sum_{n=-\infty}^{+\infty} C_n \delta(t - nT_B) hT(t)=n=−∞∑+∞Cnδ(t−nTB)

冲激响应的表达式可等效为一个由无限多的横向排列延时单元 T B T_B TB和加权系数 C n C_n Cn组成的系统，称为横向滤波器

对应的传递函数：
T ( ω ) = ∑ n = − ∞ + ∞ C n e − j ω n T B T(\omega) = \sum_{n=-\infty}^{+\infty} C_n e^{-j\omega nT_B} T(ω)=n=−∞∑+∞Cne−jωnTB

依赖 H ( ω ) H(\omega) H(ω)确定均衡器抽头系数 C n C_n Cn，可实现无ISI传输。证明略

由此，我们可以知道，当输入信号为 x ( t ) x(t) x(t)时，输出信号为：
y ( t ) = x ( t ) ∗ h T ( t ) = ∑ n = − ∞ + ∞ C n x ( t − n T B ) y(t)=x(t)*h_T(t)=\sum_{n=-\infty}^{+\infty}{C_nx(t-nT_B)} y(t)=x(t)∗hT(t)=n=−∞∑+∞Cnx(t−nTB)

有限长横向滤波器

无限多抽头的横向滤波器可以完全消除码间干扰，但物理不可实现，受体积、成本、抽头系数精度调整等制约。实际中采用 2 N + 1 2N+1 2N+1 抽头的横向滤波器：

冲激响应： e ( t ) = ∑ i = − N N C i δ ( t − i T B ) e(t) = \sum_{i=-N}^{N} C_i \delta(t - iT_B) e(t)=∑i=−NNCiδ(t−iTB)
输出信号： y ( t ) = ∑ i = − N N C i x ( t − i T B ) y(t) = \sum_{i=-N}^{N} C_i x(t - iT_B) y(t)=∑i=−NNCix(t−iTB)
抽样值： y k = ∑ i = − N N C i x k − i y_k = \sum_{i=-N}^{N} C_i x_{k-i} yk=∑i=−NNCixk−i
- y 0 y_0 y0：本码元抽样值
- y k y_k yk：码间干扰ISI

有限长横向滤波器可以减小但不能完全消除ISI。

7.4 均衡效果衡量准则

峰值失真准则

D = 1 y 0 ∑ k ≠ 0 ∣ y k ∣ D = \frac{1}{y_0} \sum_{k \neq 0} |y_k| D=y01k=0∑∣yk∣

式中，除 k = 0 k=0 k=0以外的各值的绝对值之和反映了码间串扰的最大值。 y 0 y_0 y0是有用信号样值，所以峰值失真 D D D是码间串扰最大可能值（峰值）与有用信号样值之比

均方失真准则

e 2 = 1 y 0 2 ∑ k ≠ 0 y k 2 e^2 = \frac{1}{y_0^2} \sum_{k \neq 0} y_k^2 e2=y021k=0∑yk2

其物理意义与峰值失真相似。

总结
- 峰值失真或均方失真越小，均衡效果越好，当峰值失真或均方失真为0时，无码间干扰。
- 注意：以上两种准则都是根据均衡器输出的单个脉冲响应来规定的。另外，还有必要指出，在分析横向滤波器时，我们均把时间原点(t=0)假设在滤波器中心点处（即 C 0 C_0 C0处）。如果时间参考点选择在别处，则滤波器输出的波形形状是相同的，所不同的仅仅是整个波形的提前或推迟。

7.5 迫零均衡算法（ZF）

均衡器的设计目标就是按照某种算法或者准则，求出均衡器的抽头系数，使本码元之外的所有样值 y k y_k yk为0或者趋近于0，从而消除或减小码间干扰

算法思想

调整抽头系数，迫使本码元前后各 N N N 个抽样值为零。
抽头系数求解

当初始失真 D 0 < 1 D_0 < 1 D0<1 时，抽头系数满足：

y k = { 0 k = ± 1 , ± 2 , ⋯ , ± N 1 k = 0 y_k = \begin{cases} 0 & k = \pm 1, \pm 2, \cdots, \pm N \\ 1 & k = 0 \end{cases} yk={01k=±1,±2,⋯,±Nk=0

写成矩阵形式：
X C = Y \mathbf{X} \mathbf{C} = \mathbf{Y} XC=Y

其中 Y = [ 0 , ⋯ , 0 , 1 , 0 , ⋯ , 0 ] T \mathbf{Y} = [0, \cdots, 0, 1, 0, \cdots, 0]^T Y=[0,⋯,0,1,0,⋯,0]T（仅第 N + 1 N+1 N+1 个元素为1）。

特点
- 可完全消除 2 N 2N 2N 个抽样点上的ISI
- 未考虑噪声影响，可能放大噪声（特别是信道深衰落时）

8. 部分响应技术

8.1 设计目标

提高频带利用率（达到理论极限2 Baud/Hz）
改善频谱特性
加快响应波形尾部衰减，降低对定时要求

8.2 设计思想

有控制地在某些抽样时刻引入确知的码间干扰，在接收端根据已知规则消除ISI。

8.3 第I类部分响应系统

设计思路

我们已经熟知，波形"sinx/x"拖尾严重。但通过观察sinx/x波形，我们发现相距一个码元间隔的两个sinx/x波形的＂拖尾"刚好正负相反，利用这样的波形组合肯定可以构成＂拖尾＂衰减很快的脉冲波形，依据这个思路，将两个相距 T B T_B TB 的 Sa ( π t / T B ) \text{Sa}(\pi t/T_B) Sa(πt/TB) 波形相加，得到新的响应波形：
g ( t ) = sin ⁡ ( π t / T B ) π t / T B + sin ⁡ [ π ( t − T B ) / T B ] π ( t − T B ) / T B g(t) = \frac{\sin(\pi t/T_B)}{\pi t/T_B} + \frac{\sin[\pi (t-T_B)/T_B]}{\pi (t-T_B)/T_B} g(t)=πt/TBsin(πt/TB)+π(t−TB)/TBsin[π(t−TB)/TB]

抽样特性：
g ( k T B ) = { 1 k = 0 , 1 0 其他整数 k g(kT_B) = \begin{cases} 1 & k=0,1 \\ 0 & \text{其他整数 } k \end{cases} g(kTB)={10k=0,1其他整数 k

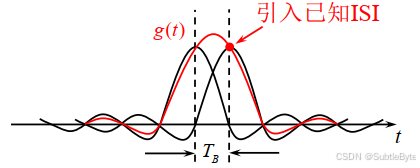
实现方法：相关编码

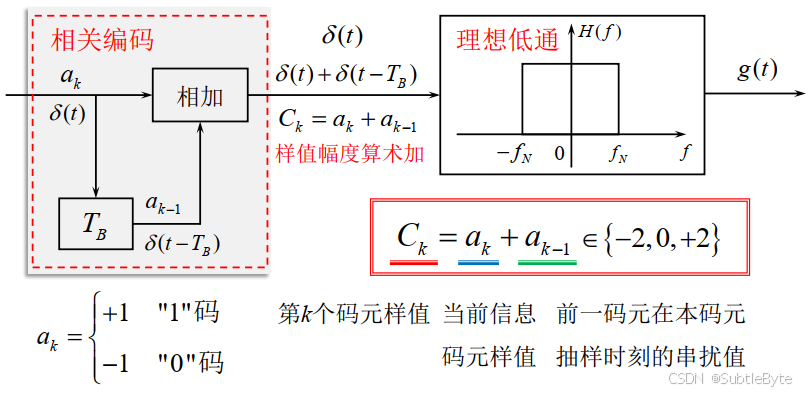
频谱特性

系统带宽： B = 1 / ( 2 T B ) = f N B = 1/(2T_B) = f_N B=1/(2TB)=fN
频带利用率： η = R B / B = 2 \eta = R_B/B = 2 η=RB/B=2 Baud/Hz
幅频特性： ∣ G ( ω ) ∣ = 2 T B cos ⁡ ( ω T B / 2 ) |G(\omega)| = 2T_B \cos(\omega T_B/2) ∣G(ω)∣=2TBcos(ωTB/2)， ∣ ω ∣ ≤ π / T B |\omega| \leq \pi/T_B ∣ω∣≤π/TB

预编码与模2判决

为避免差错传播，采用预编码：

预编码： b k = a k ⊕ b k − 1 b_k = a_k \oplus b_{k-1} bk=ak⊕bk−1
相关编码： C k = b k + b k − 1 C_k = b_k + b_{k-1} Ck=bk+bk−1（算术加）
模2判决： a k = [ C k ] mod 2 a_k = [C_k]_{\text{mod } 2} ak=[Ck]mod 2

判决规则：

C k = ± 2 C_k = \pm 2 Ck=±2 → 判"0"
C k = 0 C_k = 0 Ck=0 → 判"1"

8.4 第IV类部分响应系统

基本原理

当前码元只对下一个码元产生干扰：
g ( t ) = sin ⁡ ( π t / T B ) π t / T B − sin ⁡ [ π ( t − 2 T B ) / T B ] π ( t − 2 T B ) / T B g(t) = \frac{\sin(\pi t/T_B)}{\pi t/T_B} - \frac{\sin[\pi (t-2T_B)/T_B]}{\pi (t-2T_B)/T_B} g(t)=πt/TBsin(πt/TB)−π(t−2TB)/TBsin[π(t−2TB)/TB]

系统结构

预编码： b k = a k ⊕ b k − 2 b_k = a_k \oplus b_{k-2} bk=ak⊕bk−2
相关编码： C k = b k − b k − 2 C_k = b_k - b_{k-2} Ck=bk−bk−2
模2判决： a k = [ C k ] mod 2 a_k = [C_k]_{\text{mod } 2} ak=[Ck]mod 2

频谱特性

系统带宽： B = 1 / ( 2 T B ) = f N B = 1/(2T_B) = f_N B=1/(2TB)=fN
频带利用率： η = 2 \eta = 2 η=2 Baud/Hz
幅频特性： ∣ G ( ω ) ∣ = 2 T B sin ⁡ ( ω T B ) |G(\omega)| = 2T_B \sin(\omega T_B) ∣G(ω)∣=2TBsin(ωTB)， ∣ ω ∣ ≤ π / T B |\omega| \leq \pi/T_B ∣ω∣≤π/TB
特点：无直流分量，低频分量小

8.5 部分响应的一般形式

时域表达式

g ( t ) = ∑ m = 1 N R m sin ⁡ [ π ( t − ( m − 1 ) T B ) / T B ] π [ t − ( m − 1 ) T B ] / T B g(t) = \sum_{m=1}^{N} R_m \frac{\sin[\pi (t - (m-1)T_B)/T_B]}{\pi [t - (m-1)T_B]/T_B} g(t)=m=1∑NRmπ[t−(m−1)TB]/TBsin[π(t−(m−1)TB)/TB]

频域表达式

G ( ω ) = { T B ∑ m = 1 N R m e − j ω ( m − 1 ) T B ∣ ω ∣ ≤ π / T B 0 ∣ ω ∣ > π / T B G(\omega) = \begin{cases} T_B \sum_{m=1}^{N} R_m e^{-j\omega (m-1)T_B} & |\omega| \leq \pi/T_B \\ 0 & |\omega| > \pi/T_B \end{cases} G(ω)={TB∑m=1NRme−jω(m−1)TB0∣ω∣≤π/TB∣ω∣>π/TB

系统结构

预编码： a k = R 1 b k + R 2 b k − 1 + ⋯ + R N b k − ( N − 1 ) a_k = R_1 b_k + R_2 b_{k-1} + \cdots + R_N b_{k-(N-1)} ak=R1bk+R2bk−1+⋯+RNbk−(N−1)（模L加）
相关编码： C k = R 1 b k + R 2 b k − 1 + ⋯ + R N b k − ( N − 1 ) C_k = R_1 b_k + R_2 b_{k-1} + \cdots + R_N b_{k-(N-1)} Ck=R1bk+R2bk−1+⋯+RNbk−(N−1)（算术加）
模L判决： a k = [ C k ] mod L a_k = [C_k]_{\text{mod } L} ak=[Ck]mod L

对于L进制输入，第I、IV类部分响应信号的电平数为 2 L − 1 2L-1 2L−1。

2判决

为避免差错传播，采用预编码：

预编码： b k = a k ⊕ b k − 1 b_k = a_k \oplus b_{k-1} bk=ak⊕bk−1
相关编码： C k = b k + b k − 1 C_k = b_k + b_{k-1} Ck=bk+bk−1（算术加）
模2判决： a k = [ C k ] mod 2 a_k = [C_k]_{\text{mod } 2} ak=[Ck]mod 2

判决规则：

C k = ± 2 C_k = \pm 2 Ck=±2 → 判"0"
C k = 0 C_k = 0 Ck=0 → 判"1"

8.4 第IV类部分响应系统

基本原理

系统结构

预编码： b k = a k ⊕ b k − 2 b_k = a_k \oplus b_{k-2} bk=ak⊕bk−2
相关编码： C k = b k − b k − 2 C_k = b_k - b_{k-2} Ck=bk−bk−2
模2判决： a k = [ C k ] mod 2 a_k = [C_k]_{\text{mod } 2} ak=[Ck]mod 2

频谱特性

系统带宽： B = 1 / ( 2 T B ) = f N B = 1/(2T_B) = f_N B=1/(2TB)=fN
频带利用率： η = 2 \eta = 2 η=2 Baud/Hz
幅频特性： ∣ G ( ω ) ∣ = 2 T B sin ⁡ ( ω T B ) |G(\omega)| = 2T_B \sin(\omega T_B) ∣G(ω)∣=2TBsin(ωTB)， ∣ ω ∣ ≤ π / T B |\omega| \leq \pi/T_B ∣ω∣≤π/TB
特点：无直流分量，低频分量小

8.5 部分响应的一般形式

时域表达式

频域表达式

系统结构

预编码： a k = R 1 b k + R 2 b k − 1 + ⋯ + R N b k − ( N − 1 ) a_k = R_1 b_k + R_2 b_{k-1} + \cdots + R_N b_{k-(N-1)} ak=R1bk+R2bk−1+⋯+RNbk−(N−1)（模L加）
相关编码： C k = R 1 b k + R 2 b k − 1 + ⋯ + R N b k − ( N − 1 ) C_k = R_1 b_k + R_2 b_{k-1} + \cdots + R_N b_{k-(N-1)} Ck=R1bk+R2bk−1+⋯+RNbk−(N−1)（算术加）
模L判决： a k = [ C k ] mod L a_k = [C_k]_{\text{mod } L} ak=[Ck]mod L

对于L进制输入，第I、IV类部分响应信号的电平数为 2 L − 1 2L-1 2L−1。

由于字数限制，第二部分在博客

笔记总结内容来自：通信原理主讲：张锦皓 https://www.bilibili.com/video/BV1wA4y1f7Co?vd_source=a9099c2bbd4e16de0bbe08d30051754a

【通信原理】数字基带传输系统（二）——数字基带信号 码间干扰 均衡技术 部分响应技术（笔记总结）

第5章 数字基带传输系统 学习笔记

文章目录

5. 无码间干扰基带传输系统的抗噪声性能

5.1 分析模型

5.2 双极性信号的抗噪声性能

信号模型

判决规则

误码率分析

最佳判决门限

5.3 单极性信号的抗噪声性能

信号模型

误码率分析

最佳判决门限

5.4 性能对比

6. 眼图

7. 均衡技术

7.1 均衡的目的

7.2 均衡方法分类

7.3 时域均衡原理

横向滤波器结构

有限长横向滤波器

7.4 均衡效果衡量准则

7.5 迫零均衡算法（ZF）

8. 部分响应技术

8.1 设计目标

8.2 设计思想

8.3 第I类部分响应系统

设计思路

实现方法：相关编码

频谱特性

预编码与模2判决

8.4 第IV类部分响应系统

基本原理

系统结构

频谱特性

8.5 部分响应的一般形式

时域表达式

频域表达式

系统结构

8.4 第IV类部分响应系统

基本原理

系统结构

频谱特性

8.5 部分响应的一般形式

时域表达式

频域表达式

系统结构

【通信原理】数字基带传输系统（二）——数字基带信号码间干扰均衡技术部分响应技术（笔记总结）

第5章数字基带传输系统学习笔记