注:本文为 "PN 结" 相关合辑。
图片清晰度受引文原图所限。
略作重排,未整理去重。
如有内容异常,请看原文。
二极管反向恢复电流测试案例
炼成之路 2021 年 04 月 08 日 20:30
本文通过二极管反向恢复电流的测试案例,分析 PN 结反向恢复过程的电流特性,测试结果表明,二极管的反向恢复电流峰值可达到甚至超过正向导通电流的数值。

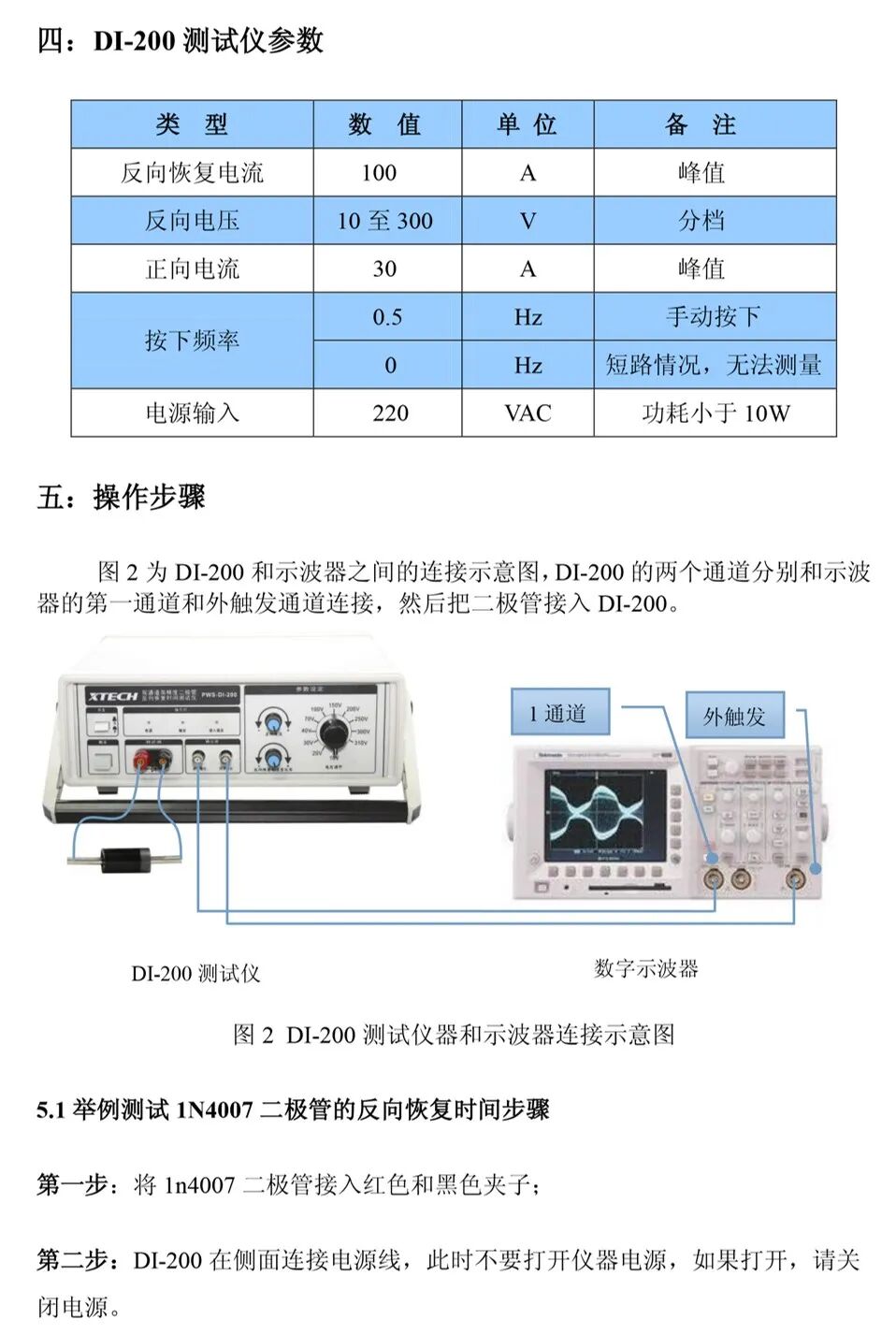
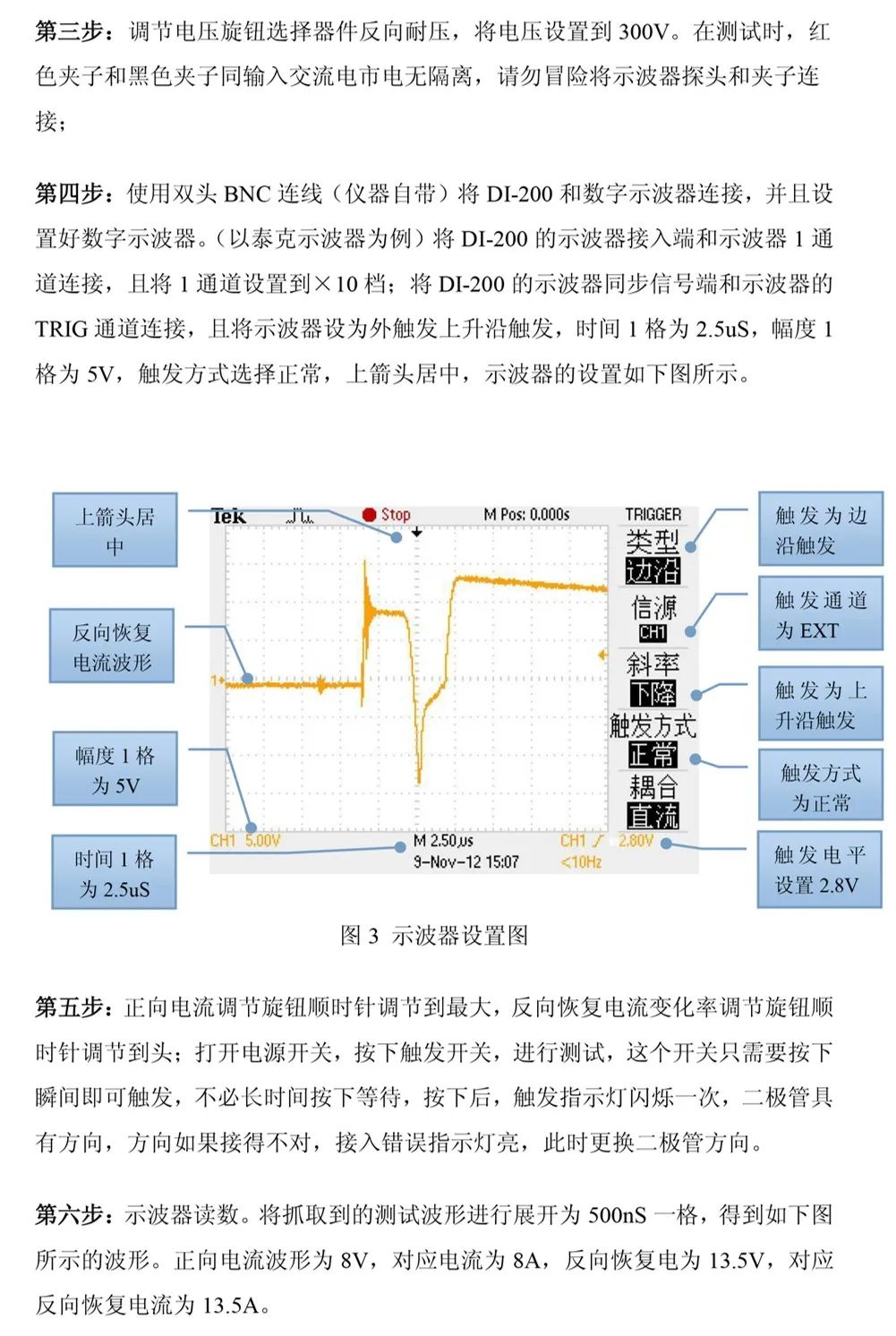
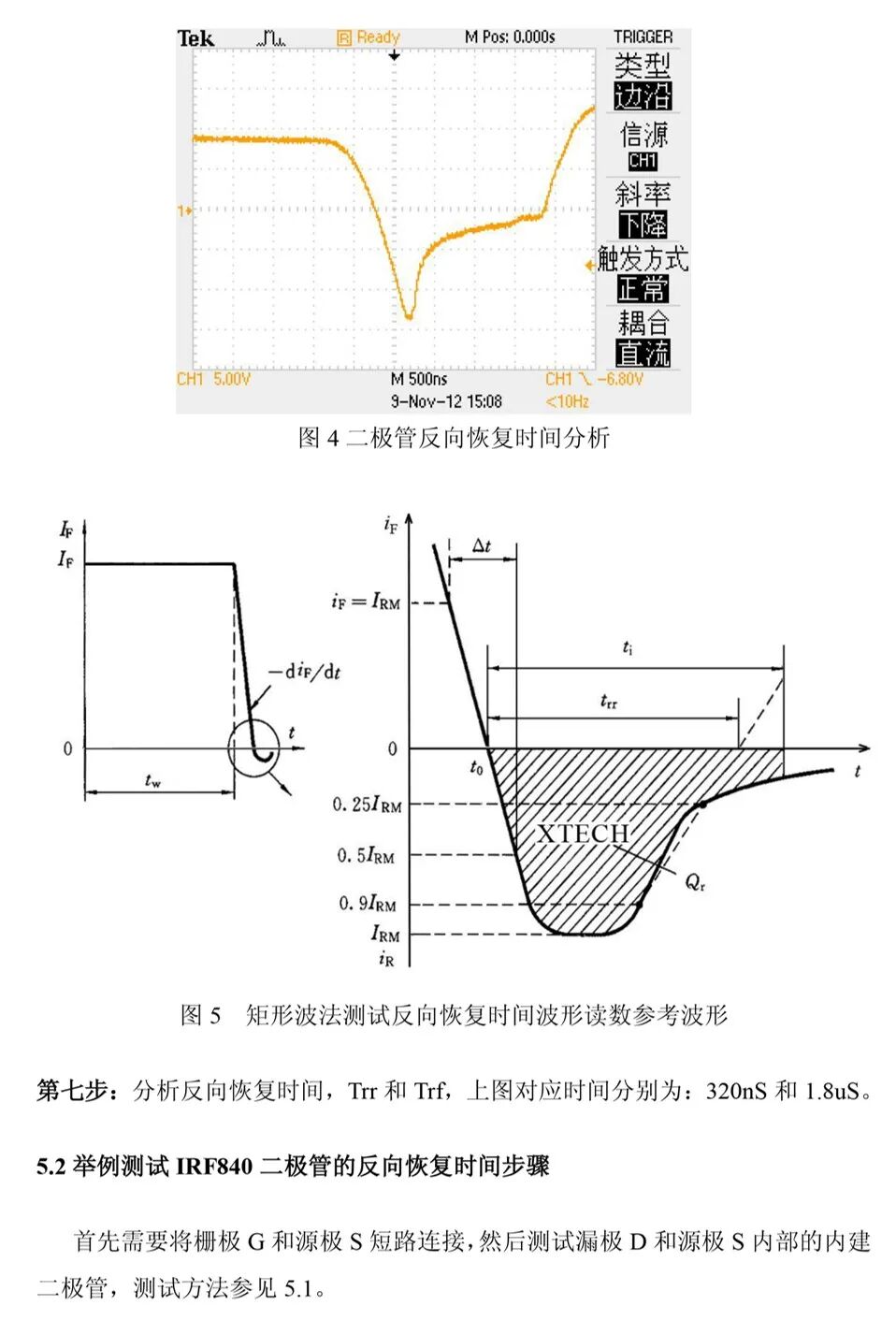
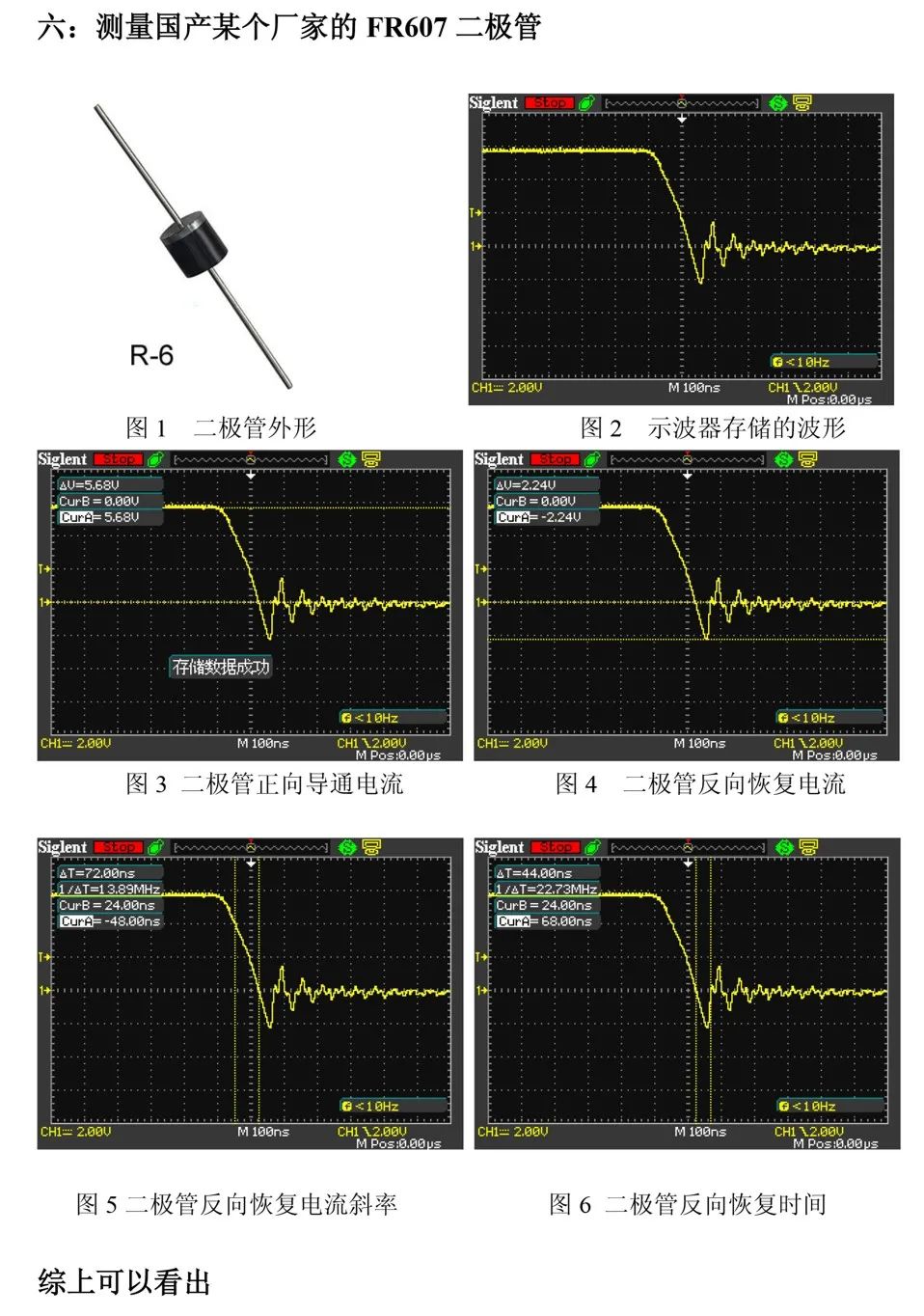
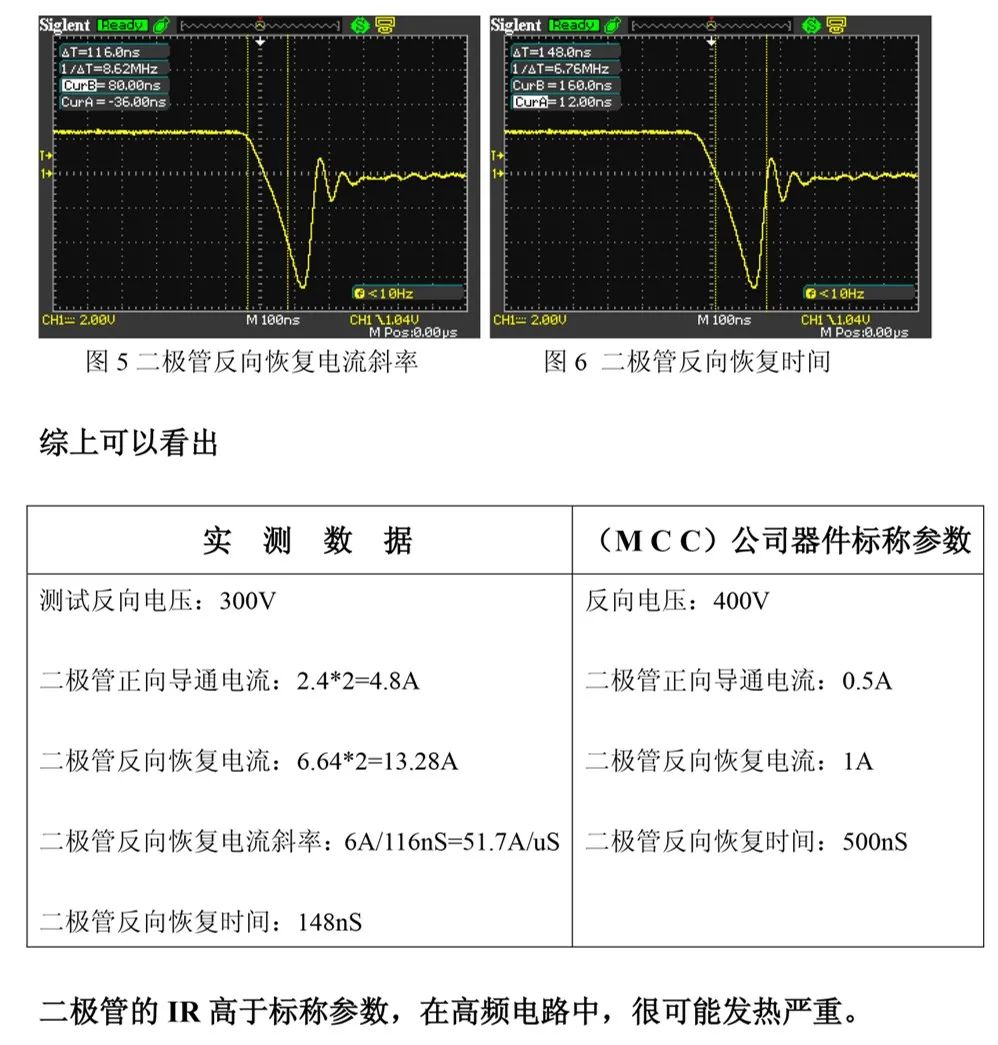
由测试结果可观察到,不同型号的二极管在反向恢复过程中呈现出明显的特性差异。测试过程中发现,测试条件与器件规格书中标注的参数测试条件存在差异,因此如何基于非标准测试条件对比测试值与标称值,成为反向恢复特性测试的待解问题。
二极管结电容和反向恢复时间的物理机理
原创 炼成之路 硬件工程师炼成之路 2021 年 4 月 6 日 20:30
本文从 PN 结的微观物理特性出发,解析二极管结电容与反向恢复时间的形成机理,明确二极管的反向恢复时间并非由规格书中标注的结电容充、放电过程决定,并对二者的关联特性进行详细说明。
结电容
二极管的两个管脚间会形成由电极产生的寄生电容,该等效电容的数值极小,相较于 PN 结的结电容可忽略不计。结电容的物理根源为 PN 结内部的电荷运动与积累特性,整体由势垒电容( C T C_{T} CT)和扩散电容( C D C_{D} CD)两部分构成,二者的形成机理存在明显差异。

势垒电容 C T C_{T} CT
根据半导体物理理论,P 区的多数载流子为空穴,N 区的多数载流子为电子。热平衡状态下,载流子因浓度梯度产生的扩散运动会在 PN 结交界面形成空间电荷区(即内建电场区/耗尽层),并产生内建电势;N 区因失去电子而带正电,P 区因获得电子而带负电,空间电荷区的内建电场会阻碍多子的扩散运动,最终达到动态平衡。
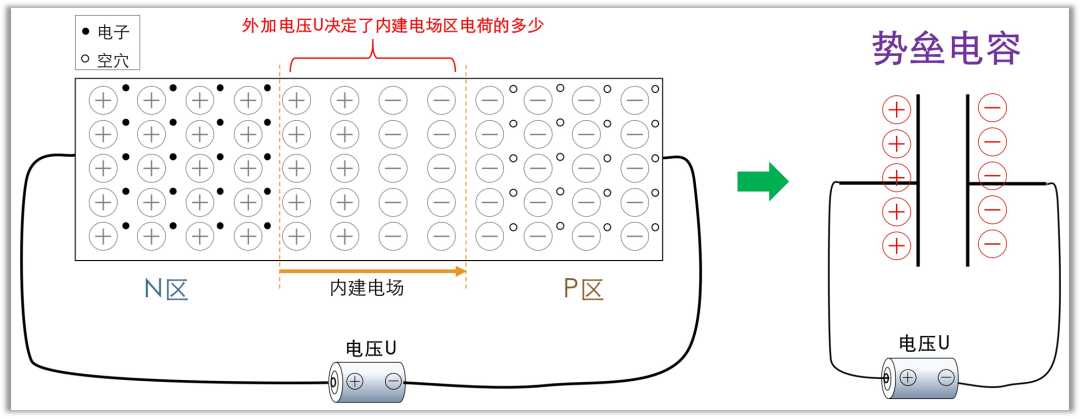
当在 PN 结两端施加稳定电压时,空间电荷区宽度达到稳态,内部电荷量恒定。若外加电压向反偏方向增大,空间电荷区宽度随之增加,内部电荷量增多;反之,若电压减小,内部电荷量减少。该现象与电容器的充放电特性相似:PN 结两端电压变化引起空间电荷区电荷数量的改变,从而呈现电容效应,该等效电容即为势垒电容 C T C_{T} CT。
势垒电容的定量表达式如下图所示:
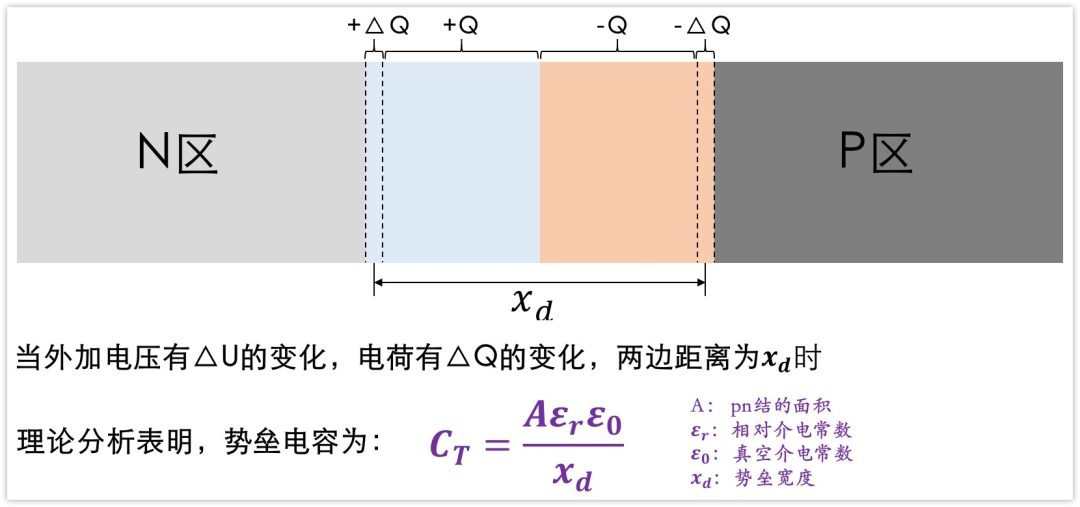
由于势垒宽度(耗尽层宽度)与外加电压相关,势垒电容的数值亦随电压变化而变化。因此,二极管数据手册中的结电容参数通常会注明测试条件,典型值为:频率 1 MHz,反偏电压 − 4 V -4\,\mathrm{V} −4V,该条件下扩散电容的容值可忽略,测试结果仅表征势垒电容的特性。

扩散电容 C D C_{D} CD
扩散电容的物理机制与非平衡少子的扩散和积累相关,其定义为:当 PN 结施加正向偏压时,在结两侧的少子扩散区内会积累一定数量的少数载流子,其浓度随外加电压变化,由此产生的附加电容效应称为扩散电容 C D C_{D} CD。
当 PN 结施加正向电压时,内建电场被削弱,由于浓度梯度驱动,P 区的空穴向 N 区扩散,N 区的电子向 P 区扩散。部分载流子在耗尽层内发生复合,另一部分载流子穿越耗尽层进入对方区域,进入对方区域的载流子为非平衡少子,不会立即与多子复合,而是在一定距离内继续扩散并参与复合。
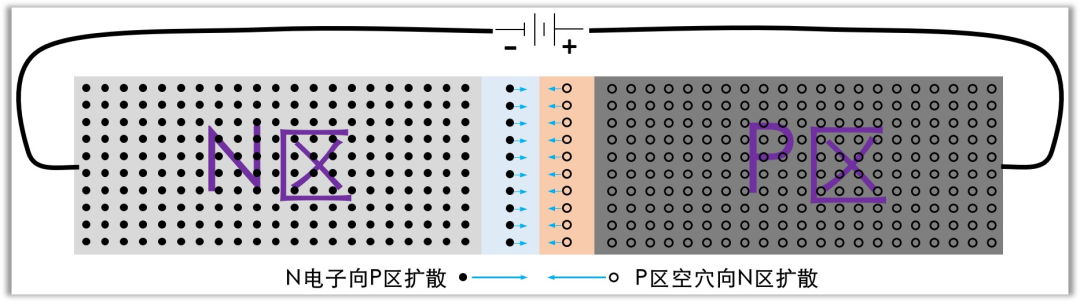
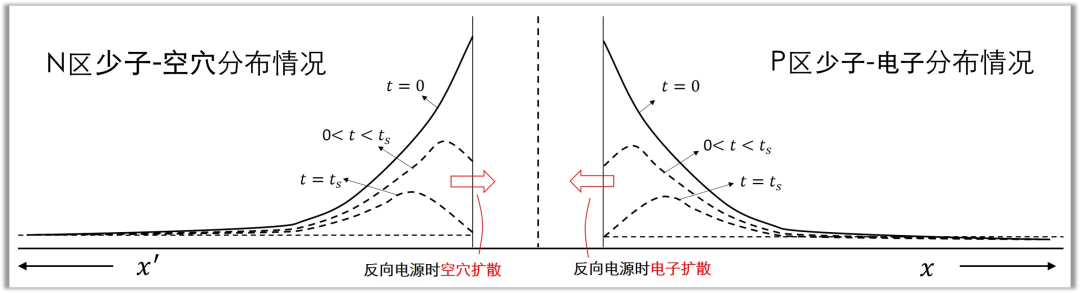
N 区中靠近空间电荷区边界处的空穴浓度最高,随距离增加浓度呈指数衰减;同理,P 区中电子浓度亦随远离结界面而降低,稳态下载流子浓度分布如下图所示。
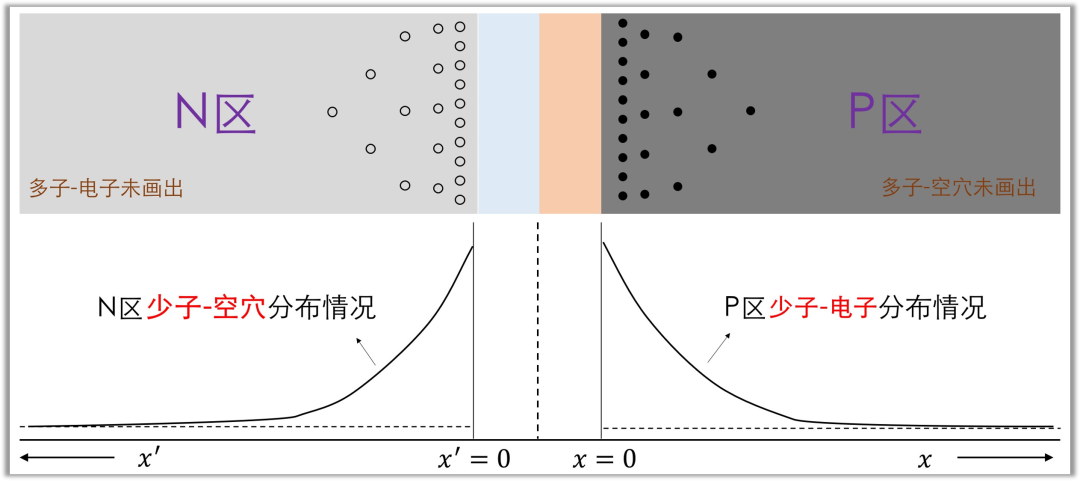
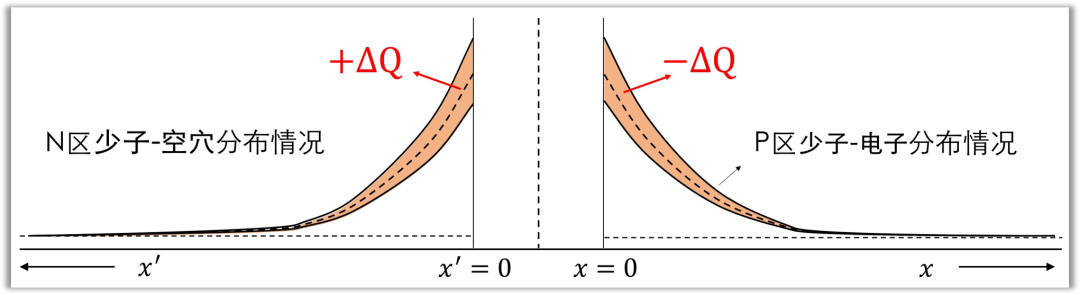
当外加电压恒定且电路达到稳态时,P 区中存储的电子数量与 N 区中存储的空穴数量保持恒定。若正向电压降低,电流减小,单位时间内注入 N 区的空穴减少,导致 N 区空穴浓度降低;同理,P 区电子浓度亦降低,稳态后存储的电荷总量减少。该特性与电容器的充放电特性等效,电压变化导致的存储电荷量变化即为扩散电容的电容效应体现。
扩散电容的定量表达式为:
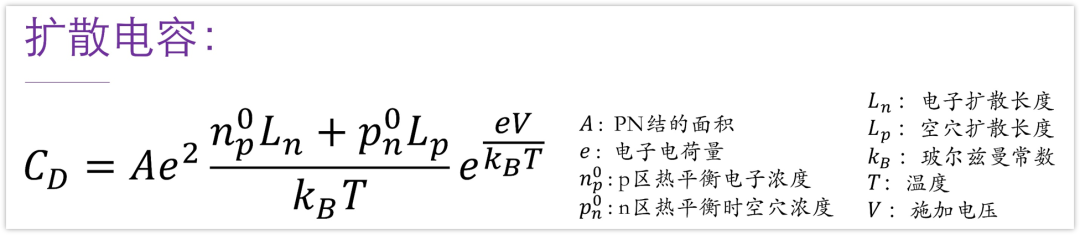
扩散电容随正向偏压按指数规律增加,故在大正向偏压条件下起主导作用;同时二极管的正向电流亦随正向偏压按指数规律变化,因此扩散电容的数值与正向电流近似成正比。
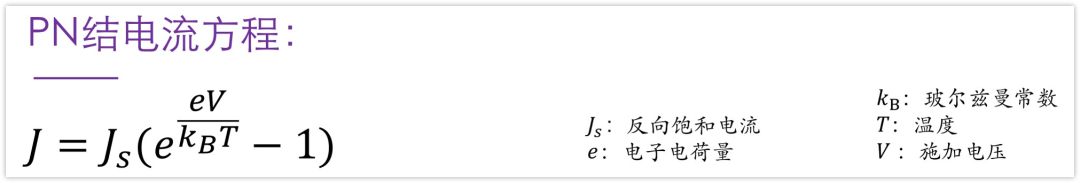
扩散电容的少子积累特性
扩散电容由非平衡少子的积累效应产生,多子的运动无法形成该电容效应,其物理机理可通过电荷中性原理解释。

少数载流子指 N 区的空穴与 P 区的电子,热平衡状态下,N 区虽以电子为多数载流子且电子带负电,但整个 N 区由硅原子与五价施主原子构成,整体呈电中性;同理,P 区也呈电中性,多子的数量远大于少子,且多子的分布均匀,电压变化无法引起多子的定向积累。
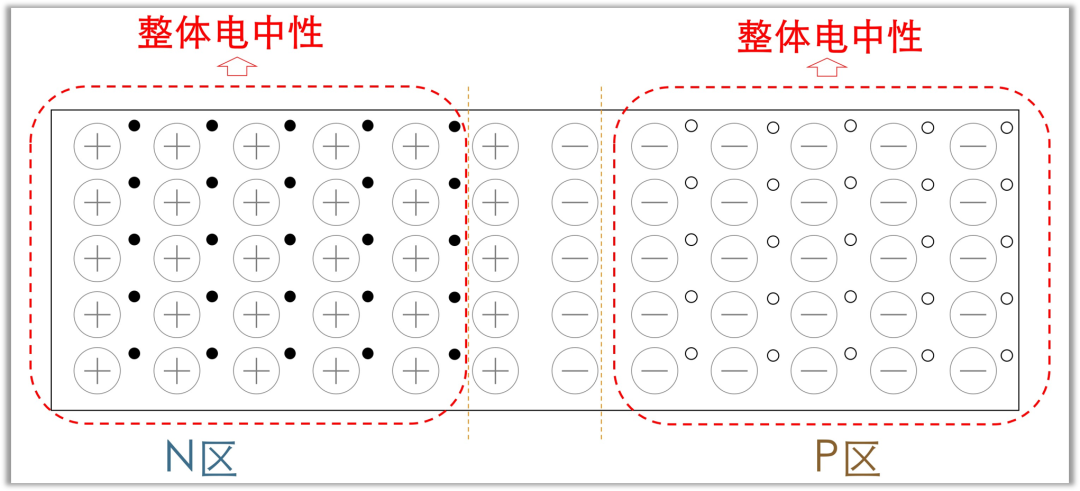
当 N 区与 P 区接触并施加正偏电压形成正向电流时,部分电子与空穴会穿越结区分别进入 P 区与 N 区。进入 P 区的电子不会立即与空穴复合,而是存在一定的寿命,此时 P 区整体呈现净负电荷,电荷量等于尚未复合的电子数量;同理,N 区呈现净正电荷,其数量等于少数载流子(空穴)数量。非平衡少子由正向偏置电压诱导产生,其分布存在明显的浓度梯度,电压变化直接导致非平衡少子的积累数量变化,进而形成电容效应。
理论分析与实验数据表明:当二极管处于反偏状态时,非平衡少子的数量极少,扩散电容的容值可忽略,结电容由势垒电容起主导作用;而在正偏状态时,扩散电容起主导作用。
反向恢复时间 t r r t_{\mathrm{rr}} trr
二极管规格书中标注的反向恢复时间 t r r t_{\mathrm{rr}} trr 为重要的动态参数,该参数决定了二极管的最高工作频率,其物理起源为 PN 结正向导通时的非平衡少子积累效应,本质上是正向导通期间 PN 结存储的非平衡少数载流子电荷被抽尽所需的时间。

反向恢复过程的物理阶段
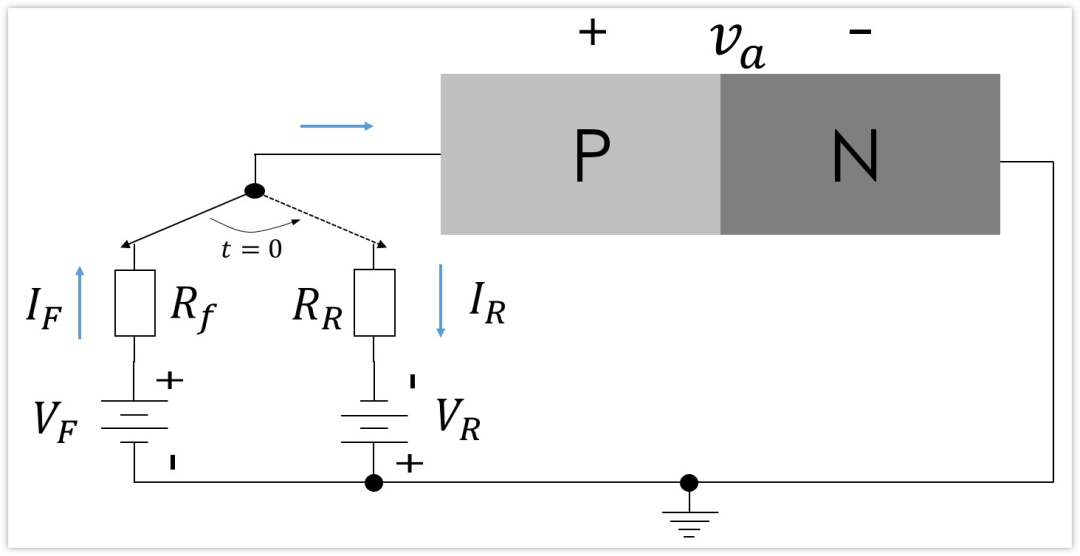
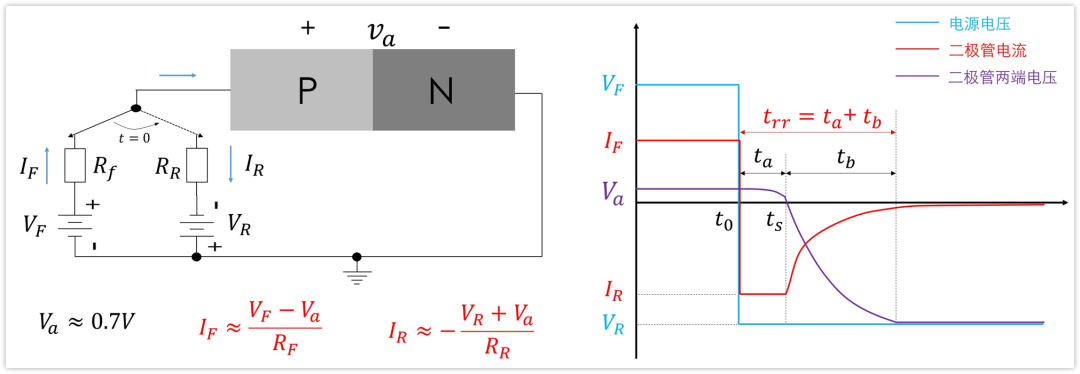
基于 PN 结的载流子运动特性,反向恢复过程可划分为四个明确的物理阶段,其过程机理可通过下图阐明:
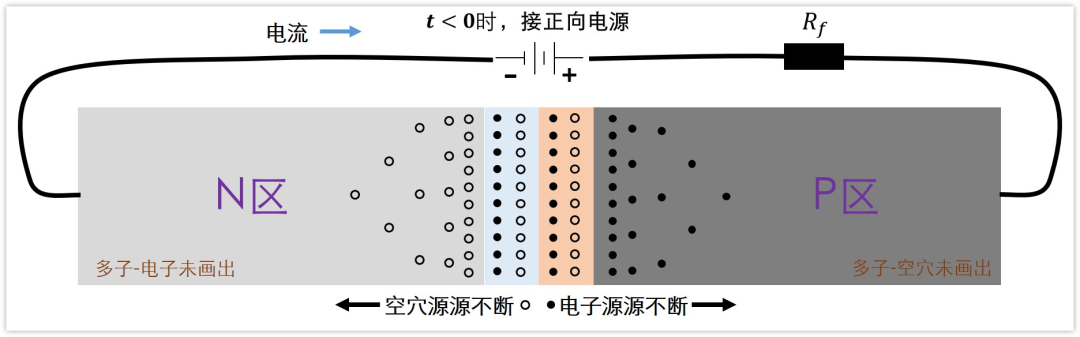
- t < 0 t < 0 t<0 阶段(正向导通阶段)
二极管施加正向偏置,正向电流为 I F = ( V F − V o n ) / R F I_{F} = (V_{F} - V_{\mathrm{on}})/R_{F} IF=(VF−Von)/RF,其中 V o n V_{\mathrm{on}} Von 为导通压降, V F V_{F} VF 为正向电源电压, R F R_{F} RF 为正向限流电阻。此时 PN 结内的耗尽层宽度较窄,扩散区内积累大量的非平衡少子,PN 结全域分布载流子,呈现良导体特性。
-
t = 0 t = 0 t=0 阶段(电压反向阶段)
电源极性迅速反转,然而此时 PN 结仍维持正偏特性。该现象的物理机制在于:PN 结反偏时空间电荷区应基本无载流子,而当前结区存储了大量非平衡载流子,在这些存储电荷被抽空前,正偏特性不会立即消失;亦可从电容角度理解,电荷未释放完毕前,结区电压无法实现突变。与此同时,结区存储电荷使二极管呈现低阻导通状态,反向电流迅速建立,其大小为 I R = ( V R + V o n ) / R R I_{R} = (V_{R} + V_{\mathrm{on}})/R_{R} IR=(VR+Von)/RR,其中 V R V_{R} VR 为反向电源电压, R R R_{R} RR 为反向限流电阻,该电流由少数载流子的反向抽取运动形成。
-
t = t s t = t_{\mathrm{s}} t=ts 阶段(耗尽层形成阶段)
PN 结中心区域的少数载流子被耗尽,空间电荷区开始重新建立,二极管逐渐恢复阻断能力。此后,P 区与 N 区中剩余的少数载流子无法继续被反向抽取,因为导电通道已被截断,结区两侧仍存在剩余载流子,其浓度分布如下图所示,反向电流的峰值出现在该阶段。
- t > t s t > t_{\mathrm{s}} t>ts 阶段(电荷复合阶段)
尽管空间电荷区已形成,电流并不会立即降为零。剩余少数载流子因浓度梯度继续向结区扩散并发生复合,该复合过程形成复合电流,此过程持续直至载流子浓度恢复至热平衡状态。从电荷平衡角度分析,P 区剩余的少数载流子(电子)使 P 区整体带负电,复合完成后 P 区恢复电中性,这些电荷经外电路返回电源,形成持续电流。
电源电压、二极管两端电压及反向电流的波形如下图所示,图中 t r r t_{\mathrm{rr}} trr 即为反向恢复时间。
反向电压尖峰的形成机理
在部分测试场景中,反向电流最大值处并非平坦,且二极管两端电压会出现反向尖峰,该波形如下图所示,两种波形的差异源于电路拓扑的不同。
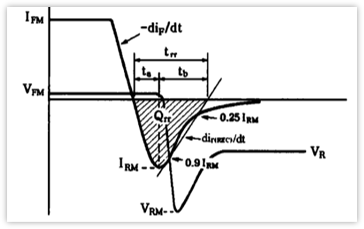
前述无尖峰的波形对应电路中含有较大串联电阻,若串联电阻极小或为零,反向电流变化率 d i / d t \mathrm{d}i/\mathrm{d}t di/dt 极大,此时电路中的分布电感或杂散电感不可忽略,电感产生的感应电动势使二极管两端出现高于电源电压的反向尖峰 V r m V_{\mathrm{rm}} Vrm。
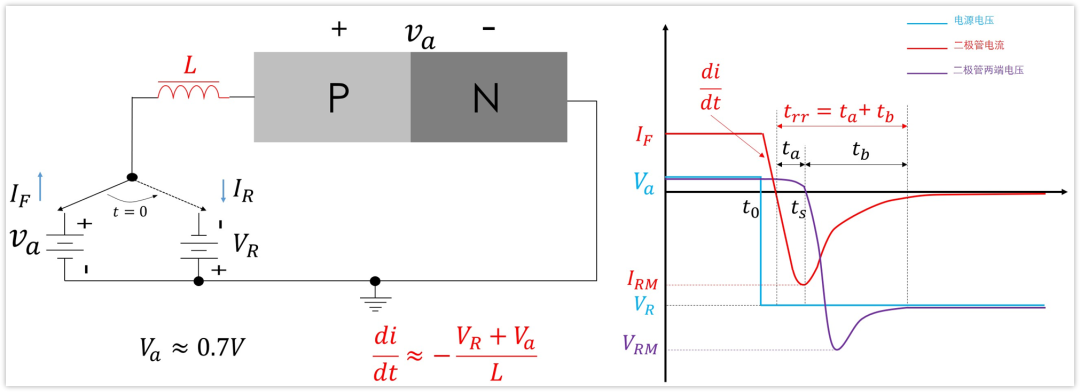
该过程的具体作用机理可按时间阶段拆解如下:
- t < 0 t < 0 t<0:电感回路中通有正向电流,电路处于初始稳态;
- t = 0 t = 0 t=0:电源极性发生突变,二极管因内部存储电荷的存在,等效为低阻导通状态,管压降极小,电路中的反向电压主要施加于电感两端,电感电流以斜率 d i / d t = ( V R + V o n ) / L \mathrm{d}i/\mathrm{d}t = (V_{R} + V_{\mathrm{on}})/L di/dt=(VR+Von)/L 呈线性下降趋势;
- t = t s t = t_{\mathrm{s}} t=ts:二极管开始恢复反向阻断能力,其反向电流达到峰值后,进入下降阶段;
- t > t s t > t_{\mathrm{s}} t>ts:二极管的导通电流转变为复合电流并逐步减小,电感因阻碍电流变化产生反向感应电压,该感应电压与电源电压叠加,导致二极管两端的反向电压高于电源电压,形成反向电压尖峰 V r m V_{\mathrm{rm}} Vrm;随着复合电流逐渐趋于零,电感两端的感应电压亦趋于零,二极管两端的电压最终稳定至电源反向电压 V R V_{R} VR。
反向恢复时间的影响因素
反向恢复时间的长短由非平衡少子的积累数量与消耗速率共同决定,主要影响因素包含以下三点:
- 反向偏置电压越小,反向恢复电流的峰值越小,非平衡少子的电荷抽取速率越低,反向恢复时间越长;
- 正向导通电流越大,扩散区内积累的非平衡少子数量越多,电荷耗尽所需的时间越长,反向恢复时间越长;
- 半导体材料的载流子复合效率越低,非平衡少子的寿命越长,电荷耗尽的时间越长,反向恢复时间越长。
结电容与反向恢复时间的关联
二极管的反向恢复时间由正向导通时的非平衡少子积累特性决定,该特性与扩散电容的形成机理直接相关,而二极管数据手册中标注的结电容参数,是在反偏条件(典型为 1 MHz、 − 4 V -4\,\mathrm{V} −4V)下测得的数值,该条件下扩散电容的容值可忽略,结电容主要表现为势垒电容。
因此可明确结论:二极管数据手册中标注的结电容主要为势垒电容,该参数与反向恢复时间无明显关联。
半导体物理------ PN 结
Leon 发布于 2023-01-22 10:26・北京
清华大学 电子信息硕士在读
本章主要讨论内容:PN 结的分类与结构、PN 结能带图、PN 结电流-电压特性、势垒宽度与势垒电容、PN 结击穿现象
一、PN 结的分类与结构
从物理本质来看,PN 结由 P 型半导体与 N 型半导体相互接触形成,实际制备过程中,通常在 N 型半导体中掺入 P 型杂质,或在 P 型半导体中掺入 N 型杂质,以此形成两种不同导电类型半导体的接触结构。杂质的掺入方法主要包括合金法与扩散法,两种方法制备的 PN 结,其差异体现在 PN 结附近的杂质浓度分布规律上。
对于合金法,以向 N 型半导体中掺入 P 型杂质为例,将铝片置于 N 型硅片表面,加热至铝熔化并与硅形成熔融体,随后降温使熔融体凝固,铝便以杂质形式掺入硅片内部。采用此法制成的 PN 结为突变结,该类型 PN 结被称为突变结的原因是,在结面处 N 型一侧的杂质浓度为恒定值 N D N_{D} ND,P 型一侧的杂质浓度即刻变为 N A N_{A} NA,通常情况下 N A N_{A} NA 与 N D N_{D} ND 存在较大数量级差异。
扩散法是通过特定的半导体工艺将 P 型杂质掺入 N 型半导体中(反之亦可),以此制备 PN 结。与合金法制备的 PN 结不同,扩散法制备的 PN 结为缓变结,其掺入的杂质浓度沿半导体接触方向呈连续渐变分布。根据半导体杂质补偿效应,当掺入杂质的浓度高于半导体原有杂质浓度时,半导体表现为掺入杂质对应的导电类型;当掺入杂质的浓度逐渐降低至低于原有杂质浓度时,半导体恢复为原有杂质对应的导电类型;掺入杂质浓度与原有杂质浓度相等的位置,即为 PN 结的结面位置。为简化理论计算,可将该杂质浓度的渐变规律近似为线性分布,其直线斜率取实际浓度变化曲线在 PN 结结面处的切线斜率;当该线性分布的斜率较大时,缓变结可近似按突变结进行分析。
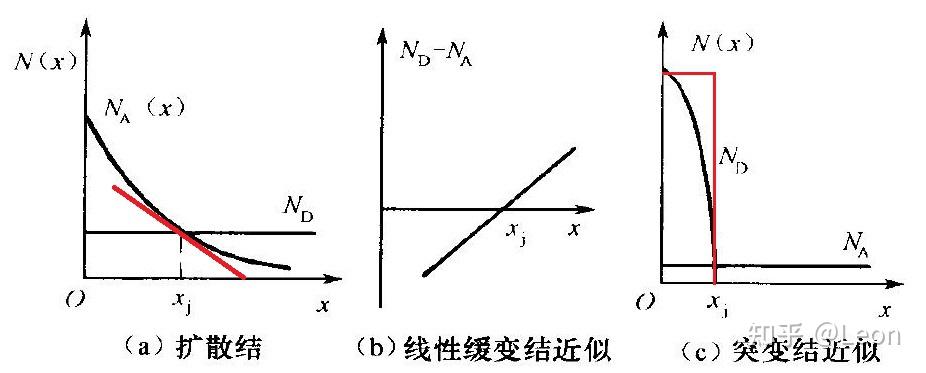
缓变结的线性近似以及突变结近似
PN 结形成后,由于 P 区的空穴浓度远高于 N 区的空穴浓度,同时 N 区的电子浓度远高于 P 区的电子浓度,因此 PN 结两侧会发生载流子的扩散运动。N 区的电子向 P 区扩散,P 区的空穴向 N 区扩散,该扩散过程会使 PN 结两侧的电中性状态被打破:紧邻结面的 P 区因失去空穴而显现出受主杂质的负电荷,N 区因失去电子而显现出施主杂质的正电荷,该区域被定义为空间电荷区,如下图所示:
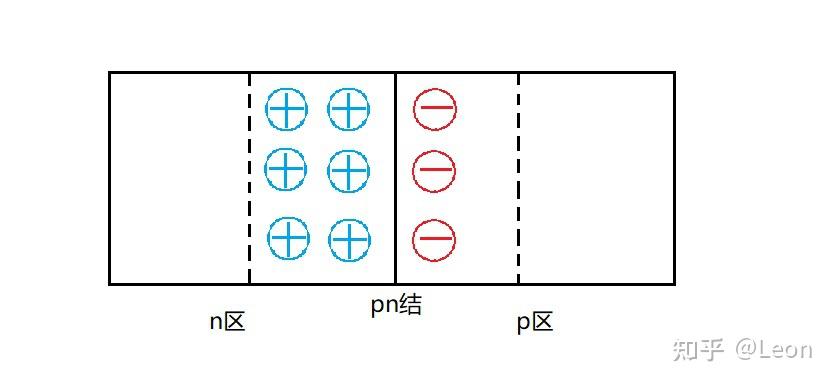
空间电荷区
空间电荷区形成后,可推知其内部会形成由 N 区指向 P 区的内建电场,该内建电场对扩散运动的载流子产生与扩散方向相反的电场力,阻碍载流子的扩散运动。最终 PN 结达到热平衡状态,空间电荷区的厚度保持恒定。该平衡为动态平衡,半导体各位置的电子、空穴浓度不随时间变化,且不同位置的载流子浓度存在差异。
由热平衡状态下空间电荷区厚度恒定的特性,可知电子电流与空穴电流的密度均为 0。载流子的电流密度由扩散流密度与内建电场引发的漂移流密度组成,据此列出电子电流密度的方程(仅考虑电子电流):
J n = n q μ n ε + D n q d n d x = 0 J_{n}=nq\mu_{n}\varepsilon+D_{n}q\frac{\mathrm{d}n}{\mathrm{d}x}=0 Jn=nqμnε+Dnqdxdn=0
需说明的是,电子浓度的计算公式 n = N c e x p ( E f − E c k T ) n=N_{c}\mathrm{exp}\left( \frac{E_{f}-E_{c}}{kT} \right) n=Ncexp(kTEf−Ec) 仍适用,但导带底的能量 E c E_{c} Ec 需叠加由 PN 结内建电场产生的电势能 − q V ( x ) -qV(x) −qV(x),此时电子的浓度表达式为 n = N c e x p ( E f − E c + q V ( x ) k T ) n=N_{c}\mathrm{exp}\left( \frac{E_{f}-E_{c}+qV(x)}{kT} \right) n=Ncexp(kTEf−Ec+qV(x))。将电子浓度公式与电场强度公式 ε = − d V ( x ) d x \varepsilon=-\frac{\mathrm{d}V(x)}{\mathrm{d}x} ε=−dxdV(x) 代入电子电流密度方程,可得:
J n = − q μ n N c exp ( E f − E c + q V ( x ) k T ) d V ( x ) d x + q D n d d x [ N c exp ( E f − E c + q V ( x ) k T ) ] = 0 \begin{aligned} J_{n} &= -q\mu_{n}N_{c}\exp\left( \frac{E_{f}-E_{c}+qV(x)}{kT} \right)\frac{\mathrm{d}V(x)}{\mathrm{d}x} \\ &\quad + qD_{n}\frac{\mathrm{d}}{\mathrm{d}x}\!\left[ N_{c}\exp\left( \frac{E_{f}-E_{c}+qV(x)}{kT} \right) \right] \\ &= 0 \end{aligned} Jn=−qμnNcexp(kTEf−Ec+qV(x))dxdV(x)+qDndxd[Ncexp(kTEf−Ec+qV(x))]=0
对上述方程做进一步化简:
− q μ n N c e x p ( E f − E c + q V ( x ) k T ) d V ( x ) d x + q D n N c e x p ( E f − E c + q V ( x ) k T ) ⋅ [ 1 k T d E f d x + q k T d V ( x ) d x ] = 0 -q\mu_{n}N_{c}\mathrm{exp}\left( \frac{E_{f}-E_{c}+qV(x)}{kT} \right)\frac{\mathrm{d}V(x)}{\mathrm{d}x}+qD_{n}N_{c}\mathrm{exp}\left( \frac{E_{f}-E_{c}+qV(x)}{kT} \right)\cdot\left[ \frac{1}{kT}\frac{\mathrm{d}E_{f}}{\mathrm{d}x}+\frac{q}{kT}\frac{\mathrm{d}V(x)}{\mathrm{d}x} \right]=0 −qμnNcexp(kTEf−Ec+qV(x))dxdV(x)+qDnNcexp(kTEf−Ec+qV(x))⋅[kT1dxdEf+kTqdxdV(x)]=0
将爱因斯坦关系 D n μ n = k T q \frac{D_{n}}{\mu_{n}}=\frac{kT}{q} μnDn=qkT 代入上式并继续化简:
q D n N c e x p ( E f − E c + q V ( x ) k T ) 1 k T d E f d x = 0 qD_{n}N_{c}\mathrm{exp}\left( \frac{E_{f}-E_{c}+qV(x)}{kT} \right)\frac{1}{kT}\frac{\mathrm{d}E_{f}}{\mathrm{d}x}=0 qDnNcexp(kTEf−Ec+qV(x))kT1dxdEf=0
由此可得 d E f d x = 0 \frac{\mathrm{d}E_{f}}{\mathrm{d}x}=0 dxdEf=0。
上述推导证明:热平衡状态下的 PN 结,其费米能级在整个半导体中处处相等。基于该结论,可构建 PN 结的能带结构图。
二、PN 结能带图
由上述分析可知,热平衡 PN 结的费米能级处处相等,而单独的 P 型半导体与 N 型半导体具有不同的费米能级------N 型半导体的费米能级更靠近导带底,P 型半导体的费米能级更靠近价带顶,二者接触形成 PN 结后,费米能级的统一通过能带的相对移动实现,具体表现为导带底与价带顶的能量位置发生偏移,最终使整个 PN 结的费米能级保持同一水平,如下图所示:
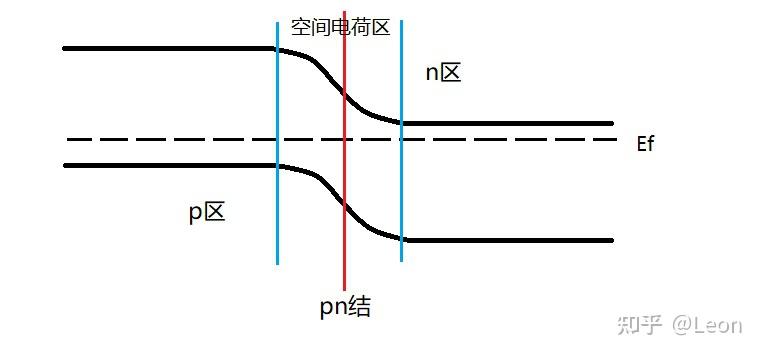
由于空间电荷区存在电场,因此电子电势能改变,导带底和价带顶也改变
由能带图可直观观察到,为实现费米能级的统一,P 区的整个能带相对 N 区的能带上移,上移的能量差为 E f n − E f p E_{fn}-E_{fp} Efn−Efp,该能量差由空间电荷区内建电场的电势差所决定。需特别注意:PN 结能带图中,空间电荷区内的价带顶与导带底的能量曲线为曲线,而非直线;后续将对该能量曲线的方程做定量推导,因此在绘制 PN 结能带图时,不可将空间电荷区的价带顶与导带底绘制成直线,该结论对缓变结与突变结均成立。
由上述分析可得,空间电荷区两端的电势差对应的能量值为 E f n − E f p E_{fn}-E_{fp} Efn−Efp。假设半导体处于非高温环境,P 区与 N 区的多数载流子主要由杂质完全电离提供,据此可分别写出 P 区与 N 区的热平衡电子浓度表达式:
(P 区中的电子浓度记为 n p 0 n_{p0} np0,P 区的导带底记为 E c p E_{cp} Ecp) n p 0 = N c e x p ( E f − E c p k T ) ≈ n i 2 N A n_{p0}=N_{c}\mathrm{exp}\left( \frac{E_f-E_{cp}}{kT} \right)\approx\frac{n_{i}^{2}}{N_{A}} np0=Ncexp(kTEf−Ecp)≈NAni2
(N 区中的电子浓度记为 n n 0 n_{n0} nn0,N 区的导带底记为 E c n E_{cn} Ecn) n n 0 = N c e x p ( E f − E c n k T ) ≈ N D n_{n0}=N_{c}\mathrm{exp}\left( \frac{E_f-E_{cn}}{kT} \right)\approx N_{D} nn0=Ncexp(kTEf−Ecn)≈ND
将上述两个电子浓度表达式作比值运算:
n p 0 n n 0 = N c e x p ( E f − E c p k T ) N c e x p ( E f − E c n k T ) = e x p ( E c n − E c p k T ) ≈ n i 2 N A N D \frac{n_{p0}}{n_{n0}}=\frac{N_{c}\mathrm{exp}\left( \frac{E_f-E_{cp}}{kT} \right)}{N_{c}\mathrm{exp}\left( \frac{E_f-E_{cn}}{kT} \right)}=\mathrm{exp}\left( \frac{E_{cn}-E_{cp}}{kT} \right)\approx\frac{n_{i}^{2}}{N_{A}N_{D}} nn0np0=Ncexp(kTEf−Ecn)Ncexp(kTEf−Ecp)=exp(kTEcn−Ecp)≈NANDni2
由此可得(设空间电荷区两端的内建电势差为 V D V_{D} VD):
q V D = E c p − E c n = − k T l n ( n i 2 N A N D ) qV_{D}=E_{cp}-E_{cn}=-kT\mathrm{ln}\left( \frac{n_{i}^{2}}{N_{A}N_{D}} \right) qVD=Ecp−Ecn=−kTln(NANDni2)
据此推导出内建电势差(亦称为势垒高度 )的表达式:
V D = k T q l n ( N A N D n i 2 ) V_{D}=\frac{kT}{q}\mathrm{ln}\left( \frac{N_{A}N_{D}}{n_{i}^{2}} \right) VD=qkTln(ni2NAND)
上述推导均基于无外加电压的热平衡状态,可见 PN 结的势垒高度与半导体的温度、掺杂浓度相关。对 PN 结施加外加电压后,其能带结构会发生相应变化,以下分正向偏压与反向偏压两种情况分析:
- 正向偏压:将 P 区接外加电源的高电位,N 区接外加电源的低电位。此时外加电场的方向与空间电荷区的内建电场方向相反,内建电场被削弱,PN 结的势垒高度降低。载流子的扩散流密度大于漂移流密度,N 区的电子向 P 区扩散形成非平衡少子电子,P 区的空穴向 N 区扩散形成非平衡少子空穴;这些非平衡少子在紧邻空间电荷区的 P 区与 N 区外侧积累,进而在 P 区和 N 区内部形成非平衡少子的扩散电流。
- 反向偏压:将 P 区接外加电源的低电位,N 区接外加电源的高电位。此时外加电场的方向与内建电场方向相同,内建电场被增强,进一步抑制了载流子的扩散运动,几乎无新的非平衡少子产生。
施加正向和反向电压的 PN 结能带图如下所示:
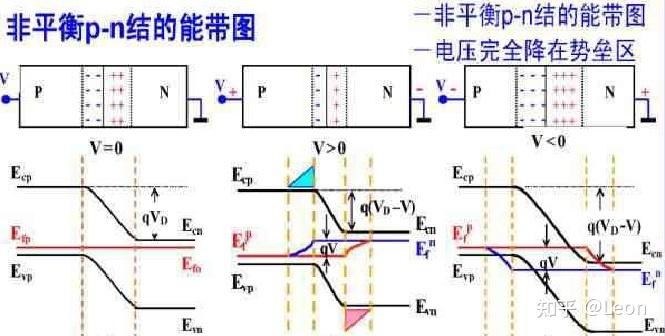
外加电压 V V V 时的 PN 结能带图
需补充说明:施加外加电压后,空间电荷区内的导带底与价带顶能量曲线仍为曲线,而非直线,部分教材中的简化能带图易造成该点的理解偏差;上述能带图中,理想 PN 结的电子准费米能级 E f n E_{fn} Efn(蓝色线)与空穴准费米能级 E f p E_{fp} Efp(红色线),在 P 区与 N 区内的变化曲线同样为曲线,后续将对上述能量曲线做定量推导。由此可解释,为何向 P 区扩散的电子与向 N 区扩散的空穴被称为非平衡少子:在外加电压作用下,紧邻空间电荷区的 P 区与 N 区内,电子与空穴的费米能级不再统一,即出现准费米能级的分裂,这是外加电场促进(正向偏压)或抑制(反向偏压)少子注入的直接结果。
三、PN 结的电流-电压特性
推导 PN 结的电流-电压特性前,先对理想 PN 结做如下基本假设,以简化理论计算:
- 外加电压全部降落在空间电荷区,空间电荷区以外的 P 区与 N 区为电中性区,区内无外加电场;因此流过 PN 结的电流仅由非平衡少子在 P 区、N 区电中性区内的扩散运动形成,无漂移电流贡献。
- 忽略空间电荷区内的载流子复合与产生过程;实际情况下,空间电荷区内的载流子复合会减少扩散的非平衡少子数量,因此理想模型的推导结果与实际值存在偏差。
基于上述假设,只需推导出 P 区内非平衡少子电子的浓度分布规律,以及 N 区内非平衡少子空穴的浓度分布规律,即可得到 PN 结的电流-电压特性。取 P 区电中性区内一微元段 x ∼ x + d x x\sim x+\mathrm{d}x x∼x+dx 进行分析(N 区的分析方法同理),如下图所示:
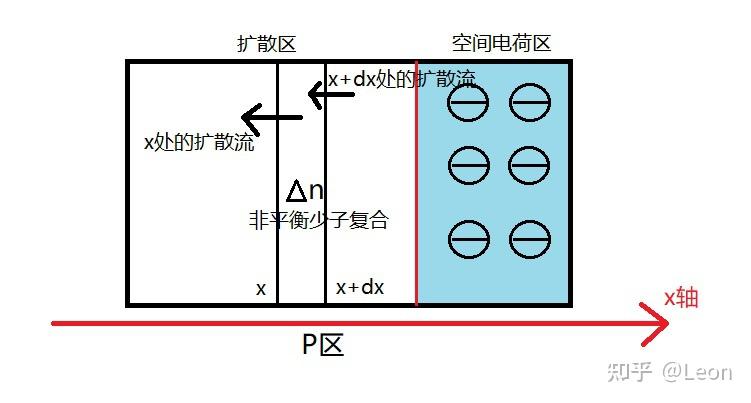
只存在扩散流情况下对微元的分析
稳态条件下,微元内的非平衡少子浓度不随时间变化,根据载流子的连续性方程,列出该微元的稳态连续性方程:
D n ( d Δ n d x ) x + d x − D n ( d Δ n d x ) x − Δ n τ n ⋅ d x = 0 D_{n}\left( \frac{\mathrm{d}\Delta n}{\mathrm{d}x} \right){x+\mathrm{d}x}-D{n}\left( \frac{\mathrm{d}\Delta n}{\mathrm{d}x} \right)_{x}-\frac{\Delta n}{\tau _{n}}\cdot \mathrm{d}x=0 Dn(dxdΔn)x+dx−Dn(dxdΔn)x−τnΔn⋅dx=0
对上述方程化简,得到非平衡少子电子的稳态扩散微分方程:
D n d 2 Δ n d x 2 − Δ n τ n = 0 D_{n}\frac{\mathrm{d}^{2}\Delta n}{\mathrm{d}x^{2}}-\frac{\Delta n}{\tau_{n}}=0 Dndx2d2Δn−τnΔn=0
该二阶常系数线性齐次微分方程的通解为:
Δ n = A e x p ( x L n ) + B e x p ( − x L n ) \Delta n=A\mathrm{exp}\left( \frac{x}{L_{n}} \right)+B\mathrm{exp}\left( -\frac{x}{L_{n}} \right) Δn=Aexp(Lnx)+Bexp(−Lnx)
其中 L n = D n τ n L_{n}=\sqrt{D_{n}\tau_{n}} Ln=Dnτn 为电子的扩散长度。
通过边界条件确定通解中的待定系数 A A A、 B B B,边界条件为扩散区与空间电荷区的结面处(设其坐标为 − x p -x_{p} −xp)的非平衡少子浓度,以及电中性区无穷远处的非平衡少子浓度。由 PN 结的能带结构可知,施加外加电压 V V V 后, − x p -x_{p} −xp 处的电子准费米能级 E f n E_{fn} Efn 向导带底移动了 q V qV qV 的能量,因此该位置的电子浓度为热平衡浓度 n p 0 n_{p0} np0 乘以 e x p ( q V k T ) \mathrm{exp}\left( \frac{qV}{kT} \right) exp(kTqV),因此结面处的非平衡少子电子浓度为:
( Δ n ) x = − x p = n p 0 [ e x p ( q V k T ) − 1 ] (\Delta n){x=-x{p}}=n_{p0}\left[ \mathrm{exp}\left( \frac{qV}{kT} \right)-1 \right] (Δn)x=−xp=np0[exp(kTqV)−1]
另一边界条件为:P 区电中性区的无穷远处,非平衡少子全部复合,浓度恢复至热平衡值,即 ( Δ n ) x = − ∞ = 0 (\Delta n){x=-\infty}=0 (Δn)x=−∞=0。将两个边界条件代入通解,解得待定系数:
B = 0 ; A = n p 0 [ e x p ( q V k T ) − 1 ] e x p ( x p L n ) B=0;A=n{p0}\left[ \mathrm{exp}\left( \frac{qV}{kT} \right)-1 \right]\mathrm{exp}\left( \frac{x_{p}}{L_{n}} \right) B=0;A=np0[exp(kTqV)−1]exp(Lnxp)
将 A A A、 B B B 代入通解,得到 P 区电中性区内非平衡少子电子的浓度分布:
Δ n = n p 0 [ e x p ( q V k T ) − 1 ] e x p ( x p + x L n ) \Delta n=n_{p0}\left[ \mathrm{exp}\left( \frac{qV}{kT} \right)-1 \right]\mathrm{exp}\left( \frac{x_{p}+x}{L_{n}} \right) Δn=np0[exp(kTqV)−1]exp(Lnxp+x)
式中, x x x 坐标的原点取在 PN 结的结面处。
同理,推导出 N 区电中性区内非平衡少子空穴的浓度分布:
Δ p = p n 0 [ e x p ( q V k T ) − 1 ] e x p ( x n − x L p ) \Delta p=p_{n0}\left[ \mathrm{exp}\left( \frac{qV}{kT} \right)-1 \right]\mathrm{exp}\left( \frac{x_{n}-x}{L_{p}} \right) Δp=pn0[exp(kTqV)−1]exp(Lpxn−x)
PN 结的总电流密度为电子扩散流密度与空穴扩散流密度的叠加,因此将 − x p -x_{p} −xp 处的电子扩散流密度与 x n x_{n} xn 处的空穴扩散流密度相加,即可得到 PN 结的总电流密度,由此得到 PN 结的总电流密度表达式:
J = J p + J n = − q D p ( d Δ p d x ) x = x n + q D n ( d Δ n d x ) x = − x p = ( q D n n p 0 L n + q D p p n 0 L p ) [ exp ( q V k T ) − 1 ] \begin{aligned} J &= J_{p}+J_{n} \\ &= -qD_{p}\left( \frac{\mathrm{d}\Delta p}{\mathrm{d}x} \right){x=x{n}}+qD_{n}\left( \frac{\mathrm{d}\Delta n}{\mathrm{d}x} \right){x=-x{p}} \\ &= \left( \frac{qD_{n}n_{p0}}{L_{n}}+\frac{qD_{p}p_{n0}}{L_{p}} \right)\left[ \exp\left( \frac{qV}{kT} \right)-1 \right] \end{aligned} J=Jp+Jn=−qDp(dxdΔp)x=xn+qDn(dxdΔn)x=−xp=(LnqDnnp0+LpqDppn0)[exp(kTqV)−1]
上式为理想 PN 结的电流-电压特性方程 。实际情况下,受空间电荷区载流子复合、大注入效应等因素的影响,电流密度与外加电压的关系偏离理想模型,其形式为 J ∝ e x p ( q V m k T ) J\propto \mathrm{exp}\left( \frac{qV}{mkT} \right) J∝exp(mkTqV),其中 1 ≤ m ≤ 2 1\leq m\leq 2 1≤m≤2, m m m 为修正系数。
基于推导出的非平衡少子浓度分布规律,可对 PN 结的准费米能级分布做进一步解释。理想 PN 结的电子准费米能级 E f n E_{fn} Efn 与空穴准费米能级 E f p E_{fp} Efp 在 P 区、N 区内呈曲线分布,其原因可由扩散区的非平衡少子浓度分布规律说明:
Δ n = n p 0 [ e x p ( q V k T ) − 1 ] e x p ( x p + x L n ) Δ p = p n 0 [ e x p ( q V k T ) − 1 ] e x p ( x n − x L p ) \Delta n=n_{p0}\left[ \mathrm{exp}\left( \frac{qV}{kT} \right)-1 \right]\mathrm{exp}\left( \frac{x_{p}+x}{L_{n}} \right)\\[6pt] \Delta p=p_{n0}\left[ \mathrm{exp}\left( \frac{qV}{kT} \right)-1 \right]\mathrm{exp}\left( \frac{x_{n}-x}{L_{p}} \right) Δn=np0[exp(kTqV)−1]exp(Lnxp+x)Δp=pn0[exp(kTqV)−1]exp(Lpxn−x)
上述两式表明,P 区与 N 区电中性区内的非平衡少子浓度沿扩散方向呈指数分布。又由非平衡载流子的浓度关系:
Δ n = n p − n p 0 = N c e x p ( E f n − E c k T ) − n p 0 Δ p = p n − p n 0 = N v e x p ( − E f p − E v k T ) − p n 0 \Delta n=n_{p}-n_{p0}=N_{c}\mathrm{exp}\left( \frac{E_{fn}-E_{c}}{kT} \right)-n_{p0}\\[6pt] \Delta p=p_{n}-p_{n0}=N_{v}\mathrm{exp}\left(- \frac{E_{fp}-E_{v}}{kT} \right)-p_{n0} Δn=np−np0=Ncexp(kTEfn−Ec)−np0Δp=pn−pn0=Nvexp(−kTEfp−Ev)−pn0
将非平衡少子浓度分布规律与上式联立,可得:
n p 0 [ e x p ( q V k T ) − 1 ] e x p ( x p + x L n ) = N c e x p ( E f n − E c k T ) − n p 0 p n 0 [ e x p ( q V k T ) − 1 ] e x p ( x n − x L p ) = N v e x p ( − E f p − E v k T ) − p n 0 n_{p0}\left[ \mathrm{exp}\left( \frac{qV}{kT} \right)-1 \right]\mathrm{exp}\left( \frac{x_{p}+x}{L_{n}} \right)=N_{c}\mathrm{exp}\left( \frac{E_{fn}-E_{c}}{kT} \right)-n_{p0}\\[6pt] p_{n0}\left[ \mathrm{exp}\left( \frac{qV}{kT} \right)-1 \right]\mathrm{exp}\left( \frac{x_{n}-x}{L_{p}} \right)=N_{v}\mathrm{exp}\left(- \frac{E_{fp}-E_{v}}{kT} \right)-p_{n0} np0[exp(kTqV)−1]exp(Lnxp+x)=Ncexp(kTEfn−Ec)−np0pn0[exp(kTqV)−1]exp(Lpxn−x)=Nvexp(−kTEfp−Ev)−pn0
由此推导出 E f n E_{fn} Efn 与 E f p E_{fp} Efp 在 P 区、N 区电中性区内的分布规律:
E f n = k T l n { n p 0 [ e x p ( q V k T ) − 1 ] e x p ( x p + x L n ) + n p 0 } + E c − k T l n N c E f p = − k T l n { p n 0 [ e x p ( q V k T ) − 1 ] e x p ( x n − x L p ) + p n 0 } + E v + k T l n N v E_{fn}=kT\mathrm{ln}\left\{ n_{p0}\left[ \mathrm{exp}\left( \frac{qV}{kT} \right)-1 \right]\mathrm{exp}\left( \frac{x_{p}+x}{L_{n}} \right)+n_{p0} \right\}+E_{c}-kT\mathrm{ln}N_{c}\\[6pt] E_{fp}=-kT\mathrm{ln}\left\{ p_{n0}\left[ \mathrm{exp}\left( \frac{qV}{kT} \right)-1 \right]\mathrm{exp}\left( \frac{x_{n}-x}{L_{p}} \right)+p_{n0} \right\}+E_{v}+kT\mathrm{ln}N_{v} Efn=kTln{np0[exp(kTqV)−1]exp(Lnxp+x)+np0}+Ec−kTlnNcEfp=−kTln{pn0[exp(kTqV)−1]exp(Lpxn−x)+pn0}+Ev+kTlnNv
物理推导验证
根据半导体物理基本关系:
- 电子浓度 : n = N c exp ( − E c − E f n k T ) n = N_c \exp\left (-\frac {E_c - E_{fn}}{kT}\right) n=Ncexp(−kTEc−Efn)
- 空穴浓度 : p = N v exp ( − E f p − E v k T ) p = N_v \exp\left (-\frac {E_{fp} - E_v}{kT}\right) p=Nvexp(−kTEfp−Ev)
反解准费米能级:
E f n = E c + k T ln n N c = k T ln n ⏟ 分布项 + E c − k T ln N c ⏟ 常数项 E_{fn} = E_c + kT\ln\frac {n}{N_c} = \underbrace {kT\ln n}{\text {分布项}} + \underbrace {E_c - kT\ln N_c}{\text {常数项}} Efn=Ec+kTlnNcn=分布项 kTlnn+常数项 Ec−kTlnNcE f p = E v + k T ln N v p = − k T ln p ⏟ 分布项 + E v + k T ln N v ⏟ 常数项 E_{fp} = E_v + kT\ln\frac {N_v}{p} = \underbrace {-kT\ln p}{\text {分布项}} + \underbrace {E_v + kT\ln N_v}{\text {常数项}} Efp=Ev+kTlnpNv=分布项 −kTlnp+常数项 Ev+kTlnNv
在 P 区电中性区,非平衡电子浓度:
n ( x ) = n p 0 [ exp ( q V k T ) − 1 ] exp ( x p + x L n ) + n p 0 n (x) = n_{p0}\left [\exp\left (\frac {qV}{kT}\right)-1\right]\exp\left (\frac {x_p+x}{L_n}\right)+n_{p0} n(x)=np0[exp(kTqV)−1]exp(Lnxp+x)+np0
其分布曲线的形态如下图所示(以 P 区电中性区内的 E f n E_{fn} Efn 为例):
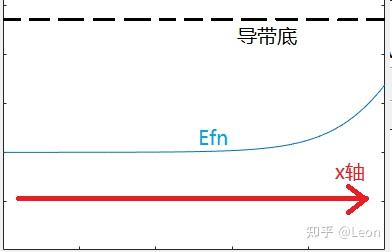
四、势垒宽度与势垒电容
本节对 PN 结空间电荷区的势垒宽度与势垒电容做定量分析。由前文可知,根据制备工艺的差异,PN 结可分为突变结与缓变结两类,二者的差异体现在空间电荷区内的电荷体密度分布规律上。
突变结的空间电荷区内,电荷体密度的分布满足:
ρ ( x ) = { − q N A , − x p < x < 0 q N D , 0 < x < x n \rho(x)= \begin{cases} -qN_{\text{A}}, & -x_p < x < 0 \\[2pt] qN_{\text{D}}, & 0 < x < x_n \end{cases} ρ(x)={−qNA,qND,−xp<x<00<x<xn
式中,P 区的电荷体密度由受主杂质的负电荷贡献,N 区的电荷体密度由施主杂质的正电荷贡献,结面处的电荷体密度发生阶跃式突变。
对缓变结做线性近似后,其空间电荷区内的电荷体密度呈线性分布,表达式为:
ρ ( x ) = q α x ( − x p < x < x n ) \rho(x)=q\alpha x\ (-x_{p}<x<x_{n}) ρ(x)=qαx (−xp<x<xn)
其中 α \alpha α 为电荷体密度的线性变化斜率,可见电荷体密度沿 x x x 方向呈均匀变化。基于不同的电荷体密度分布,突变结与缓变结的空间电荷区内,电势分布规律存在差异,以下分别推导。
推导前,先由静电场的高斯定理推导一维情况下的泊松方程,为后续电势分布的计算奠定基础。假设电荷体密度仅沿 x x x 方向变化,取 x ∼ x + d x x\sim x+\mathrm{d}x x∼x+dx 的一维微元段进行分析,如下图所示:
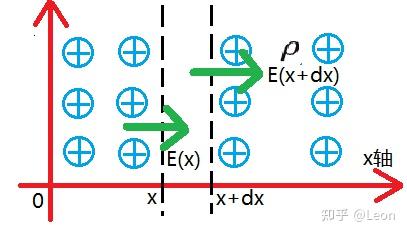
对该微元段构建高斯面------高斯面为垂直于 x x x 轴、横截面积为 A A A 的柱体,柱体的轴向厚度为 d x \mathrm{d}x dx,对其应用静电场高斯定理:
E ( x + d x ) ⋅ A − E ( x ) ⋅ A = ρ ( x ) A d x ε 0 ε r E(x+\mathrm{d}x)\cdot A-E(x)\cdot A=\frac{\rho(x)A\mathrm{d}x}{\varepsilon_{0}\varepsilon_{r}} E(x+dx)⋅A−E(x)⋅A=ε0εrρ(x)Adx
对上述式子化简,得到电场强度与电荷体密度的关系:
d E ( x ) d x = ρ ( x ) ε 0 ε r \frac{\mathrm{d}E(x)}{\mathrm{d}x}=\frac{\rho(x)}{\varepsilon_{0}\varepsilon_{r}} dxdE(x)=ε0εrρ(x)
结合电场强度与电势的关系 ε = − d V ( x ) d x \varepsilon=-\frac{\mathrm{d}V(x)}{\mathrm{d}x} ε=−dxdV(x),推导出一维泊松方程 :
d 2 V ( x ) d x 2 = − ρ ( x ) ε 0 ε r \frac{\mathrm{d}^{2}V(x)}{\mathrm{d}x^{2}}=-\frac{\rho(x)}{\varepsilon_{0}\varepsilon_{r}} dx2d2V(x)=−ε0εrρ(x)
(一)突变结的势垒宽度与电势分布
首先分析突变结,通过求解泊松方程,得到其空间电荷区的电场强度与电势分布规律。将 PN 突变结的电荷体密度分布 ρ ( x ) \rho(x) ρ(x) 代入一维泊松方程,得到分段的泊松方程:
d 2 V ( x ) d x 2 = { q N A ε 0 ε r , − x p < x < 0 − q N D ε 0 ε r , 0 < x < x n \frac{\mathrm{d}^2 V(x)}{\mathrm{d}x^2}= \begin{cases} \displaystyle\frac{qN_{\text{A}}}{\varepsilon_0 \varepsilon_r}, & -x_p < x < 0 \\[6pt] -\displaystyle\frac{qN_{\text{D}}}{\varepsilon_0 \varepsilon_r}, & 0 < x < x_n \end{cases} dx2d2V(x)=⎩ ⎨ ⎧ε0εrqNA,−ε0εrqND,−xp<x<00<x<xn
对分段的泊松方程做一次积分,结合电场强度与电势的关系 ε = − d V ( x ) d x \varepsilon=-\frac{\mathrm{d}V(x)}{\mathrm{d}x} ε=−dxdV(x),得到空间电荷区内电场强度的通解:
ε ( x ) = { − q N A ε 0 ε r x + A , − x p < x < 0 q N D ε 0 ε r x + B , 0 < x < x n \varepsilon(x)= \begin{cases} -\dfrac{qN_{\text{A}}}{\varepsilon_0 \varepsilon_r}x + A, & -x_p < x < 0 \\[6pt] \dfrac{qN_{\text{D}}}{\varepsilon_0 \varepsilon_r}x + B, & 0 < x < x_n \end{cases} ε(x)=⎩ ⎨ ⎧−ε0εrqNAx+A,ε0εrqNDx+B,−xp<x<00<x<xn
根据空间电荷区边界电场为 0 的条件( x = − x p x=-x_p x=−xp、 x = x n x=x_n x=xn 处 ε = 0 \varepsilon=0 ε=0),代入 P、N 区电场通解,可直接求得待定系数:
A = − q N A x p ε 0 ε r , B = − q N D x n ε 0 ε r A=-\frac{qN_{A}x_{p}}{\varepsilon_{0}\varepsilon_{r}},\quad B=-\frac{qN_{D}x_{n}}{\varepsilon_{0}\varepsilon_{r}} A=−ε0εrqNAxp,B=−ε0εrqNDxn
将待定系数代入通解,得到突变结空间电荷区的电场强度分段表达式:
ε ( x ) = { − q N A ( x + x p ) ε 0 ε r , − x p < x < 0 q N D ( x − x n ) ε 0 ε r , 0 < x < x n \varepsilon(x)= \begin{cases} -\dfrac{qN_{\text{A}}(x+x_p)}{\varepsilon_0 \varepsilon_r}, & -x_p < x < 0 \\[6pt] \dfrac{qN_{\text{D}}(x-x_n)}{\varepsilon_0 \varepsilon_r}, & 0 < x < x_n \end{cases} ε(x)=⎩ ⎨ ⎧−ε0εrqNA(x+xp),ε0εrqND(x−xn),−xp<x<00<x<xn
由该表达式可知,突变结空间电荷区内的电场强度呈线性分布,结面( x = 0 x=0 x=0)处的电场强度为最大值 ,且满足电荷守恒条件 N A x p = N D x n N_{A}x_{p}=N_{D}x_{n} NAxp=NDxn(空间电荷区内正负电荷总量相等),据此可推导出结面处的最大电场强度 ε m = − q N A x p ε 0 ε r = − q N D x n ε 0 ε r \varepsilon_{m}=-\frac{qN_{A}x_{p}}{\varepsilon_{0}\varepsilon_{r}}=-\frac{qN_{D}x_{n}}{\varepsilon_{0}\varepsilon_{r}} εm=−ε0εrqNAxp=−ε0εrqNDxn(负号表示电场方向由 N 区指向 P 区)。
突变结空间电荷区的电荷密度与电场强度分布如下图所示:
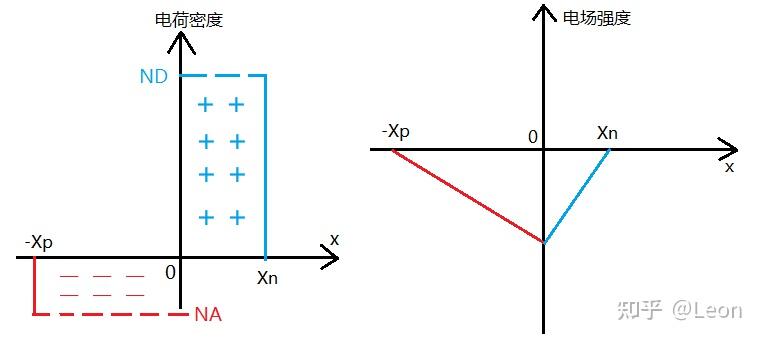
突变 PN 结空间电荷区的电荷密度以及与之对应的电场强度图像
接下来推导突变结的电势分布,设定电势参考点 为 x = − x p x=-x_{p} x=−xp 处( V ( − x p ) = 0 V(-x_{p})=0 V(−xp)=0),利用电势与电场强度的积分关系 V ( x ) = − ∫ − x p x ε ( x ) d x V(x)=-\int_{-x_{p}}^{x}\varepsilon(x)\mathrm{d}x V(x)=−∫−xpxε(x)dx,对电场强度分段积分,得到电势的分段表达式:
V ( x ) = { q N A ( x + x p ) 2 2 ε 0 ε r , − x p < x < 0 q N A x p ( x p + 2 x ) 2 ε 0 ε r + q N D ( x n 2 − x 2 ) 2 ε 0 ε r , 0 < x < x n V(x)= \begin{cases} \dfrac{qN_{\text{A}}(x+x_p)^2}{2\varepsilon_0 \varepsilon_r}, & -x_p < x < 0 \\[6pt] \dfrac{qN_{\text{A}}x_p(x_p+2x)}{2\varepsilon_0 \varepsilon_r} + \dfrac{qN_{\text{D}}(x_n^2-x^2)}{2\varepsilon_0 \varepsilon_r}, & 0 < x < x_n \end{cases} V(x)=⎩ ⎨ ⎧2ε0εrqNA(x+xp)2,2ε0εrqNAxp(xp+2x)+2ε0εrqND(xn2−x2),−xp<x<00<x<xn
空间电荷区两端的势垒高度为 x = x n x=x_{n} x=xn 处的电势值,即 V D = V ( x n ) V_{D}=V(x_{n}) VD=V(xn),将 x = x n x=x_{n} x=xn 代入上述 N 区电势表达式,结合电荷守恒条件 N A x p = N D x n N_{A}x_{p}=N_{D}x_{n} NAxp=NDxn,化简可得:
V D = q 2 ε 0 ε r ⋅ N A N D ( x p + x n ) 2 N A + N D V_{D}=\frac{q}{2\varepsilon_{0}\varepsilon_{r}}\cdot\frac{N_{A}N_{D}(x_{p}+x_{n})^{2}}{N_{A}+N_{D}} VD=2ε0εrq⋅NA+NDNAND(xp+xn)2
定义势垒宽度 X D = x p + x n X_{D}=x_{p}+x_{n} XD=xp+xn(空间电荷区的总厚度),将其代入上式,整理得到势垒宽度与势垒高度的关系:
X D = 2 ε 0 ε r V D q ⋅ N A + N D N A N D X_{D}=\sqrt{\frac{2\varepsilon_{0}\varepsilon_{r}V_{D}}{q}\cdot\frac{N_{A}+N_{D}}{N_{A}N_{D}}} XD=q2ε0εrVD⋅NANDNA+ND
当对 PN 结施加正向偏压 V V V(P 区接高电势)时,内建势垒被削弱为 V D − V V_{D}-V VD−V,此时势垒宽度随偏压变化的表达式为:
X D = 2 ε 0 ε r ( V D − V ) q ⋅ N A + N D N A N D X_{D}=\sqrt{\frac{2\varepsilon_{0}\varepsilon_{r}(V_{D}-V)}{q}\cdot\frac{N_{A}+N_{D}}{N_{A}N_{D}}} XD=q2ε0εr(VD−V)⋅NANDNA+ND
若施加反向偏压,只需将 V V V 取负值代入上式,此时势垒高度增大,势垒宽度相应展宽。
(二)缓变结的势垒宽度与电势分布
对缓变结做线性近似 后,其空间电荷区内的电荷体密度呈线性分布,表达式为 ρ ( x ) = q α x ( − x p < x < x n ) \rho(x)=q\alpha x\ (-x_{p}<x<x_{n}) ρ(x)=qαx (−xp<x<xn),其中 α \alpha α 为电荷体密度的线性变化斜率,表征杂质浓度的渐变速率。
将线性电荷体密度分布代入一维泊松方程,得到缓变结的泊松方程:
d 2 V ( x ) d x 2 = − q α x ε 0 ε r ( − x p < x < x n ) \frac{\mathrm{d}^{2}V(x)}{\mathrm{d}x^{2}}=-\frac{q\alpha x}{\varepsilon_{0}\varepsilon_{r}}\ (-x_{p}<x<x_{n}) dx2d2V(x)=−ε0εrqαx (−xp<x<xn)
结合缓变结的边界条件求解该方程,边界条件为:空间电荷区边界电场强度为0,即 ε ( − x p ) = 0 \varepsilon(-x_{p})=0 ε(−xp)=0、 ε ( x n ) = 0 \varepsilon(x_{n})=0 ε(xn)=0;电势参考点取 x = − x p x=-x_{p} x=−xp 处,即 V ( − x p ) = 0 V(-x_{p})=0 V(−xp)=0。同时,线性缓变结的空间电荷区呈对称分布,满足 x p = x n = X D 2 x_{p}=x_{n}=\frac{X_{D}}{2} xp=xn=2XD( X D X_{D} XD 为缓变结的势垒宽度)。
对泊松方程做第一次积分,结合 ε = − d V ( x ) d x \varepsilon=-\frac{\mathrm{d}V(x)}{\mathrm{d}x} ε=−dxdV(x),得到电场强度表达式:
ε ( x ) = − q α 2 ε 0 ε r ( x 2 − x p 2 ) \varepsilon(x)=-\frac{q\alpha}{2\varepsilon_{0}\varepsilon_{r}}(x^{2}-x_{p}^{2}) ε(x)=−2ε0εrqα(x2−xp2)
再对电场强度做积分,代入电势参考点与对称条件,得到缓变结的电势分布:
V ( x ) = − q α x 3 6 ε r ε 0 + q α x X D 2 8 ε r ε 0 + q α 3 ε r ε 0 ( X D 2 ) 3 V(x) = -\frac{q\alpha x^3}{6\varepsilon_r \varepsilon_0} + \frac{q\alpha x X_D^2}{8\varepsilon_r \varepsilon_0} + \frac{q\alpha}{3\varepsilon_r \varepsilon_0} \left( \frac{X_D}{2} \right)^3 V(x)=−6εrε0qαx3+8εrε0qαxXD2+3εrε0qα(2XD)3
将 x = x p = X D 2 x=x_{p}=\frac{X_{D}}{2} x=xp=2XD 代入电势表达式,得到势垒高度 V D = V ( x p ) V_{D}=V(x_{p}) VD=V(xp),化简后得到缓变结势垒宽度与势垒高度的关系:
X D = ( 12 ε 0 ε r V D q α ) 1 3 X_{D}=\left( \frac{12\varepsilon_{0}\varepsilon_{r}V_{D}}{q\alpha} \right)^{\frac{1}{3}} XD=(qα12ε0εrVD)31
当施加正向偏压 V V V 时,内建势垒变为 V D − V V_{D}-V VD−V,缓变结的势垒宽度随偏压变化的表达式为:
X D = [ 12 ε 0 ε r ( V D − V ) q α ] 1 3 X_{D}=\left[ \frac{12\varepsilon_{0}\varepsilon_{r}(V_{D}-V)}{q\alpha} \right]^{\frac{1}{3}} XD=[qα12ε0εr(VD−V)]31
与突变结不同,缓变结的势垒宽度与 ( V D − V ) (V_{D}-V) (VD−V) 呈1/3次方关系 ,而突变结的势垒宽度与 ( V D − V ) (V_{D}-V) (VD−V) 呈1/2次方关系,该差异源于二者空间电荷区内的电荷体密度分布规律不同。
结合突变结与缓变结的电势分布表达式可知,空间电荷区内的电势 V ( x ) V(x) V(x) 分别为二次函数与三次函数,而电子的电势能为 − q V ( x ) -qV(x) −qV(x),导带底 E c E_{c} Ec 与价带顶 E v E_{v} Ev 的能量与电子电势能直接相关,因此空间电荷区内的导带底与价带顶均为曲线而非直线 ,二者的电势与能带变化关系如下图所示:
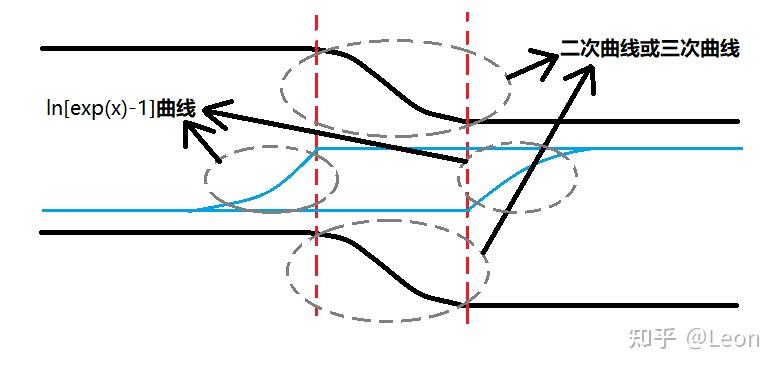
(三)PN 结的势垒电容
PN 结的空间电荷区为高阻区,区内的可移动载流子几乎被耗尽,仅存在固定的电离杂质电荷。当外加电压发生变化时,空间电荷区的厚度(势垒宽度)会相应改变,导致区内的电离杂质电荷量发生变化,这种电荷量随外加电压的变化特性 表现出电容效应,该电容被称为势垒电容 ,记为 C B C_{B} CB。
由于势垒宽度随外加电压非线性变化,势垒电容为变容二极管 的核心参数,需采用微分电容 的定义进行描述,即单位面积的势垒电容 C T C_{T} CT 为单位面积上的电荷量 Q Q Q 对外加电压 V V V 的微分:
C T = d Q d V C_{T}=\frac{\mathrm{d}Q}{\mathrm{d}V} CT=dVdQ
若 PN 结的横截面积为 A A A,则 PN 结的总势垒电容为 C B = A ⋅ C T C_{B}=A\cdot C_{T} CB=A⋅CT,以下分别推导突变结与缓变结的单位面积势垒电容表达式。
1. 突变结的势垒电容
突变结的单位面积空间电荷电荷量由电离杂质电荷决定,结合电荷守恒 N A x p = N D x n N_{A}x_{p}=N_{D}x_{n} NAxp=NDxn,取 P 区的电离杂质电荷为参考,单位面积电荷量 Q = q N A x p Q=qN_{A}x_{p} Q=qNAxp。
将突变结的 x p x_{p} xp 与势垒宽度 X D X_{D} XD 的关系 x p = N D N A + N D X D x_{p}=\frac{N_{D}}{N_{A}+N_{D}}X_{D} xp=NA+NDNDXD,以及势垒宽度随电压变化的表达式代入 Q Q Q,再对 V V V 求微分,结合 C T = d Q d V C_{T}=\frac{\mathrm{d}Q}{\mathrm{d}V} CT=dVdQ,化简得到突变结的单位面积势垒电容 :
C T = ε 0 ε r q 2 ( V D − V ) ⋅ N A N D N A + N D C_{T}=\sqrt{\frac{\varepsilon_{0}\varepsilon_{r}q}{2(V_{D}-V)}\cdot\frac{N_{A}N_{D}}{N_{A}+N_{D}}} CT=2(VD−V)ε0εrq⋅NA+NDNAND
该式表明,突变结的单位面积势垒电容与 ( V D − V ) − 1 / 2 (V_{D}-V)^{-1/2} (VD−V)−1/2 成正比,反向偏压越大,势垒电容越小。
2. 缓变结的势垒电容
线性缓变结的单位面积电荷量为空间电荷区**单侧(如N区)**的电荷量(因电荷守恒,P区与N区电荷量相等),即对N区( 0 < x < x n 0 < x < x_n 0<x<xn)的电荷体密度积分:
Q = ∫ 0 x n ρ ( x ) d x Q=\int_{0}^{x_n}\rho(x)\mathrm{d}x Q=∫0xnρ(x)dx
代入电荷密度 ρ ( x ) = q α x \rho(x)=q\alpha x ρ(x)=qαx 与对称条件 x p = x n = X D 2 x_{p}=x_{n}=\frac{X_{D}}{2} xp=xn=2XD,积分得:
Q = q α X D 2 8 Q=\frac{q\alpha X_{D}^{2}}{8} Q=8qαXD2
将缓变结势垒宽度随电压变化的表达式代入上式,再对 V V V 求微分,结合势垒电容定义 C T = d Q d V C_{T}=\frac{\mathrm{d}Q}{\mathrm{d}V} CT=dVdQ,化简得到缓变结的单位面积势垒电容 :
C T = [ q α ε 0 2 ε r 2 12 ( V D − V ) ] 1 3 C_{T}=\left[ \frac{q\alpha \varepsilon_{0}^{2}\varepsilon_{r}^{2}}{12(V_{D}-V)} \right]^{\frac{1}{3}} CT=[12(VD−V)qαε02εr2]31
缓变结的单位面积势垒电容与 ( V D − V ) − 1 / 3 (V_{D}-V)^{-1/3} (VD−V)−1/3 成正比,其随反向偏压的变化速率慢于突变结。
五、PN 结的击穿
当对 PN 结施加的反向偏压 增大至某一临界值时,PN 结的反向电流会突然呈现出急剧增大的现象,该现象被称为PN 结的击穿 ,对应的临界反向偏压被称为击穿电压 ,记为 V B R V_{BR} VBR。
PN 结击穿的本质是反向偏压过大时,空间电荷区内的载流子数量发生雪崩式倍增,导致反向电流急剧增大。根据击穿的物理机理,可将 PN 结击穿分为电击穿 与热击穿 两大类,其中电击穿为可逆的物理过程,热击穿为不可逆的损坏过程;电击穿又可进一步分为雪崩击穿 与齐纳击穿两种类型。
(一)雪崩击穿
雪崩击穿 是高掺杂浓度、宽势垒区 PN 结的主要击穿形式,其物理机理为载流子的碰撞电离。
当 PN 结的反向偏压增大时,空间电荷区的内建电场随之增强,区内的少数载流子在强电场的作用下获得足够大的漂移动能。当载流子的动能大于半导体晶格的电离能时,载流子与晶格原子发生碰撞,会将晶格共价键中的电子激发至导带,同时产生一个空穴,该过程被称为碰撞电离。
碰撞电离产生的电子与空穴会在强电场中继续被加速,进而引发新的碰撞电离,产生更多的载流子;该过程不断迭代,使空间电荷区内的载流子数量呈雪崩式倍增,最终导致 PN 结的反向电流急剧增大,形成雪崩击穿。
雪崩击穿的发生存在两个必要条件:
① 空间电荷区的电场强度足够大,能使载流子获得电离所需的动能;
② 空间电荷区具有足够的厚度,为载流子提供足够的加速距离,保证碰撞电离的发生。
因此,雪崩击穿多发生在低掺杂的 PN 结中------低掺杂 PN 结的势垒宽度较宽,且击穿电压随掺杂浓度的降低而增大。
(二)齐纳击穿
齐纳击穿 又被称为隧道击穿 ,是低掺杂浓度、窄势垒区 PN 结的主要击穿形式,其物理机理为量子隧穿效应。
高掺杂的 PN 结中,杂质浓度的提高会使空间电荷区的势垒宽度大幅减窄(可至 10 nm 以下)。当反向偏压增大时,空间电荷区的能带会发生剧烈倾斜,当满足能量关系 q V D > Δ E g qV_D > \Delta E_g qVD>ΔEg 时,N 区的导带底能量甚至会低于 P 区的价带顶能量,此时 P 区价带中的电子无需克服禁带的能量壁垒,可通过量子隧穿效应直接穿过窄势垒区进入 N 区的导带,成为导电的载流子。
当反向偏压增大至临界值时,大量价带电子通过隧穿效应进入导带,使 PN 结的反向电流急剧增大,形成齐纳击穿。齐纳击穿的击穿电压较低(一般小于 6 V),且击穿电压随掺杂浓度的提高而降低,与雪崩击穿的变化趋势相反。
实际的 PN 结中,击穿电压在 6 V 左右时,雪崩击穿与齐纳击穿会同时发生,被称为混合击穿;击穿电压大于 6 V 时,以雪崩击穿为主;击穿电压小于 6 V 时,以齐纳击穿为主。
(三)热击穿
热击穿 是 PN 结在反向偏压下的不可逆损坏过程,其物理机理为温度与反向电流的正反馈效应。
PN 结施加反向偏压时,会产生反向漏电流,漏电流在 PN 结的体电阻上产生焦耳热,使 PN 结的温度升高。半导体的本征载流子浓度 n i n_{i} ni 随温度呈指数增长,当温度升高时,PN 结的反向漏电流会随之增大;反向漏电流的增大会产生更多的焦耳热,进一步提高 PN 结的温度,形成温度-反向电流的正反馈。
当该正反馈过程无法被有效散热抑制时,PN 结的温度会持续升高,最终导致半导体的晶格熔化、PN 结的结构被永久性损坏,即发生热击穿。
热击穿与雪崩击穿、齐纳击穿的本质区别在于:
① 热击穿为不可逆过程,会造成 PN 结的永久性损坏,而电击穿为可逆过程,撤去反向偏压后 PN 结可恢复正常;
② 热击穿的发生与 PN 结的散热条件直接相关,而电击穿由半导体的掺杂浓度、势垒宽度等固有参数决定。因此,实际应用中需为 PN 结设计合理的散热结构,防止热击穿的发生。
via:
- 二极管结电容和反向恢复时间都是怎么来的 - 知乎
https://zhuanlan.zhihu.com/p/362772737
半导体物理------ PN 结 - 知乎
https://zhuanlan.zhihu.com/p/599798230