动态时间规整(Dynamic Time Warping,DTW)
flyfish
传统距离要求两个序列严格一对一索引对齐(等长是前提),而 DTW 允许序列间多对一、一对多的弹性对齐.动态时间规整(Dynamic Time Warping,DTW)是一种专为时序序列设计的相似性度量算法,解决传统距离算法(欧氏、曼哈顿等)无法处理的序列不等长、时间轴畸变(偏移/拉伸/压缩)问题,通过弹性的时间对齐找到两个序列间的最优匹配路径,再计算该路径下的最小累积距离,以此衡量序列的相似性。
python
import numpy as np
import matplotlib.pyplot as plt
from scipy.spatial.distance import cdist
def dtw_calculate(seq1, seq2, dist='euclidean'):
"""
计算DTW距离和最优对齐路径
:param seq1: 序列1 (一维数组)
:param seq2: 序列2 (一维数组)
:param dist: 距离度量方式,默认欧氏距离
:return: dtw_distance (DTW距离), cost_matrix (成本矩阵), path (最优对齐路径)
"""
# 转换为numpy数组
seq1 = np.array(seq1).reshape(-1, 1)
seq2 = np.array(seq2).reshape(-1, 1)
# 1. 计算两两元素的距离矩阵(局部成本)
distance_matrix = cdist(seq1, seq2, metric=dist)
m, n = distance_matrix.shape
# 2. 初始化累积成本矩阵
cost_matrix = np.zeros((m+1, n+1))
cost_matrix[0, 1:] = np.inf # 第一行(除(0,0))设为无穷大
cost_matrix[1:, 0] = np.inf # 第一列(除(0,0))设为无穷大
cost_matrix[0, 0] = 0 # 起点
# 3. 填充累积成本矩阵
for i in range(1, m+1):
for j in range(1, n+1):
cost_matrix[i, j] = distance_matrix[i-1, j-1] + min(
cost_matrix[i-1, j], # 上
cost_matrix[i, j-1], # 左
cost_matrix[i-1, j-1] # 对角线
)
# 4. 回溯找最优路径(从右下角到左上角)
i, j = m, n
path = []
while i > 0 and j > 0:
path.append((i-1, j-1)) # 转换为原始序列的索引(从0开始)
# 找最小的前驱节点
min_prev = min(cost_matrix[i-1, j], cost_matrix[i, j-1], cost_matrix[i-1, j-1])
if min_prev == cost_matrix[i-1, j-1]:
i -= 1
j -= 1
elif min_prev == cost_matrix[i-1, j]:
i -= 1
else:
j -= 1
path.reverse() # 反转路径,从起点到终点
# 5. DTW距离为累积成本矩阵的最后一个元素
dtw_distance = cost_matrix[m, n]
return dtw_distance, cost_matrix[1:, 1:], path
# ===================== 主程序 =====================
# 定义的序列
x = [3, 1, 2, 2, 1]
y = [2, 0, 0, 3, 3, 1, 0]
# 计算DTW
dtw_dist, cost_mat, align_path = dtw_calculate(x, y)
print(f"DTW距离: {dtw_dist}")
print(f"最优对齐路径 (x索引, y索引): {align_path}")
# ===================== 可视化(含索引标注) =====================
fig, (ax1, ax2) = plt.subplots(2, 1, figsize=(10, 8))
# 子图1:原始序列 + 精准DTW对齐路径 + 索引标注
# 绘制x序列(红色)
x_indices = np.arange(len(x))
ax1.plot(x_indices, x, 'o-', color='red', label='Sequence x', markersize=8)
# 绘制y序列(蓝色)
y_indices = np.arange(len(y))
ax1.plot(y_indices, y, 's-', color='blue', label='Sequence y', markersize=8)
# 核心1:精准绘制每个对齐点的连线
for (i, j) in align_path:
ax1.plot([i, j], [x[i], y[j]], 'k--', alpha=0.6, linewidth=1.5)
# 核心2:为x序列标注索引(x0, x1, x2...)
for idx, val in enumerate(x):
# 标注位置:点的上方0.1个单位,居中对齐,红色字体
ax1.text(idx, val + 0.15, f'x{idx}', fontsize=9, ha='center', va='bottom', color='red', fontweight='bold')
# 核心3:为y序列标注索引(y0, y1, y2...)
for idx, val in enumerate(y):
# 标注位置:点的下方0.15个单位,居中对齐,蓝色字体
ax1.text(idx, val - 0.2, f'y{idx}', fontsize=9, ha='center', va='top', color='blue', fontweight='bold')
# 子图1样式设置
ax1.set_xlabel('Index', fontsize=10)
ax1.set_ylabel('Value', fontsize=10)
ax1.set_title('Original Sequences with Accurate DTW Alignment', fontsize=11)
ax1.legend(loc='upper right', fontsize=9)
ax1.grid(True, alpha=0.3)
# 确保x轴范围覆盖两个序列的索引,y轴留出标注空间
ax1.set_xlim(-0.5, max(len(x), len(y)) - 0.5)
ax1.set_ylim(-0.5, max(max(x), max(y)) + 0.5)
# 子图2:DTW成本矩阵 + 最优路径
im = ax2.imshow(cost_mat, cmap='viridis', aspect='auto')
ax2.set_xlabel('Sequence y Index', fontsize=10)
ax2.set_ylabel('Sequence x Index', fontsize=10)
ax2.set_title('DTW Cost Matrix and Optimal Path', fontsize=11)
# 绘制最优路径
path_x = [p[1] for p in align_path]
path_y = [p[0] for p in align_path]
ax2.plot(path_x, path_y, 'r-', linewidth=2)
ax2.scatter(path_x, path_y, color='red', s=50, zorder=5)
# 添加颜色条
cbar = plt.colorbar(im, ax=ax2)
cbar.set_label('Cumulative Cost', fontsize=9)
# 调整布局,避免标注被裁剪
plt.tight_layout()
# 保存图片(可选,dpi=300保证高清)
# plt.savefig('dtw_visualization_with_labels.png', dpi=300, bbox_inches='tight')
plt.show()x = [ 3 , 1 , 2 , 2 , 1 ] x=[3,1,2,2,1] x=[3,1,2,2,1](长度5)
y = [ 2 , 0 , 0 , 3 , 3 , 1 , 0 ] y=[2,0,0,3,3,1,0] y=[2,0,0,3,3,1,0](长度7)
为什么传统距离算法不适用?
序列为例: x = [ 3 , 1 , 2 , 2 , 1 ] x=[3,1,2,2,1] x=[3,1,2,2,1](长度5)、 y = [ 2 , 0 , 0 , 3 , 3 , 1 , 0 ] y=[2,0,0,3,3,1,0] y=[2,0,0,3,3,1,0](长度7),首先不满足等长要求,无法直接用欧氏/曼哈顿距离;即使强行补零等长,也会因时间轴畸变导致形状相似的位置无法对齐,计算出的距离完全偏离实际相似性。
而DTW的就是打破一对一索引对齐的限制,让序列的形状特征而非索引位置成为匹配依据。
DTW的原理
以两个任意时序序列 X = [ x 0 , x 1 , . . . , x m − 1 ] X=[x_0,x_1,...,x_{m-1}] X=[x0,x1,...,xm−1](长度 m m m)、 Y = [ y 0 , y 1 , . . . , y n − 1 ] Y=[y_0,y_1,...,y_{n-1}] Y=[y0,y1,...,yn−1](长度 n n n)为例,DTW的计算流程和逻辑为4步,全程围绕局部距离矩阵和累积成本矩阵 展开
步骤1:构建局部距离矩阵 D \boldsymbol{D} D
计算两个序列中每一对元素的局部距离(常用欧氏距离,一维下为绝对值),形成 m × n m \times n m×n的矩阵 D D D,其中元素 D [ i ] [ j ] D[i][j] D[i][j]表示 x i x_i xi与 y j y_j yj的局部距离:
D [ i ] [ j ] = d ( x i , y j ) ( i = 0 , 1 , . . . , m − 1 ; j = 0 , 1 , . . . , n − 1 ) D[i][j] = d(x_i, y_j) \quad (i=0,1,...,m-1; \ j=0,1,...,n-1) D[i][j]=d(xi,yj)(i=0,1,...,m−1; j=0,1,...,n−1)
d ( ⋅ ) d(\cdot) d(⋅)为距离度量(欧氏、曼哈顿等,按需选择)。
步骤2:初始化累积成本矩阵 C \boldsymbol{C} C
构建 ( m + 1 ) × ( n + 1 ) (m+1) \times (n+1) (m+1)×(n+1)的累积成本矩阵 C C C,用于记录从序列起点 ( x 0 , y 0 ) (x_0,y_0) (x0,y0)到位置 ( x i , y j ) (x_i,y_j) (xi,yj)的最小累积距离,初始化规则为:
{ C [ 0 ] [ 0 ] = 0 (起点累积成本为0) C [ 0 ] [ j ] = ∞ ( j > 0 ) (第一行:无前置x元素,无法对齐) C [ i ] [ 0 ] = ∞ ( i > 0 ) (第一列:无前置y元素,无法对齐) \begin{cases} C[0][0] = 0 \quad \text{(起点累积成本为0)} \\ C[0][j] = \infty \quad (j>0) \quad \text{(第一行:无前置x元素,无法对齐)} \\ C[i][0] = \infty \quad (i>0) \quad \text{(第一列:无前置y元素,无法对齐)} \end{cases} ⎩ ⎨ ⎧C[0][0]=0(起点累积成本为0)C[0][j]=∞(j>0)(第一行:无前置x元素,无法对齐)C[i][0]=∞(i>0)(第一列:无前置y元素,无法对齐)
∞ \infty ∞的作用是排除无意义的对齐路径,确保路径从起点 ( 0 , 0 ) (0,0) (0,0)开始。
步骤3:填充累积成本矩阵 C \boldsymbol{C} C(递推)
按行/列遍历矩阵,通过递推公式计算每个位置的最小累积成本------到达 ( x i , y j ) (x_i,y_j) (xi,yj)的累积成本 = 当前局部距离 D [ i − 1 ] [ j − 1 ] D[i-1][j-1] D[i−1][j−1] + 从上方、左方、左上方三个方向来的最小前驱累积成本(三个方向对应三种对齐方式:x多对一、y多对一、一对一):
C [ i ] [ j ] = D [ i − 1 ] [ j − 1 ] + min ( C [ i − 1 ] [ j ] , C [ i ] [ j − 1 ] , C [ i − 1 ] [ j − 1 ] ) C[i][j] = D[i-1][j-1] + \min\left(C[i-1][j], C[i][j-1], C[i-1][j-1]\right) C[i][j]=D[i−1][j−1]+min(C[i−1][j],C[i][j−1],C[i−1][j−1])
( i = 1 , 2 , . . . , m ; j = 1 , 2 , . . . , n ) (i=1,2,...,m; \ j=1,2,...,n) (i=1,2,...,m; j=1,2,...,n)
步骤4:回溯找最优对齐路径 + 计算DTW距离
- DTW距离:累积成本矩阵的右下角元素 C [ m ] [ n ] C[m][n] C[m][n] 即为两个序列的DTW距离,代表最优对齐路径下的最小累积距离,值越小表示序列相似性越高;
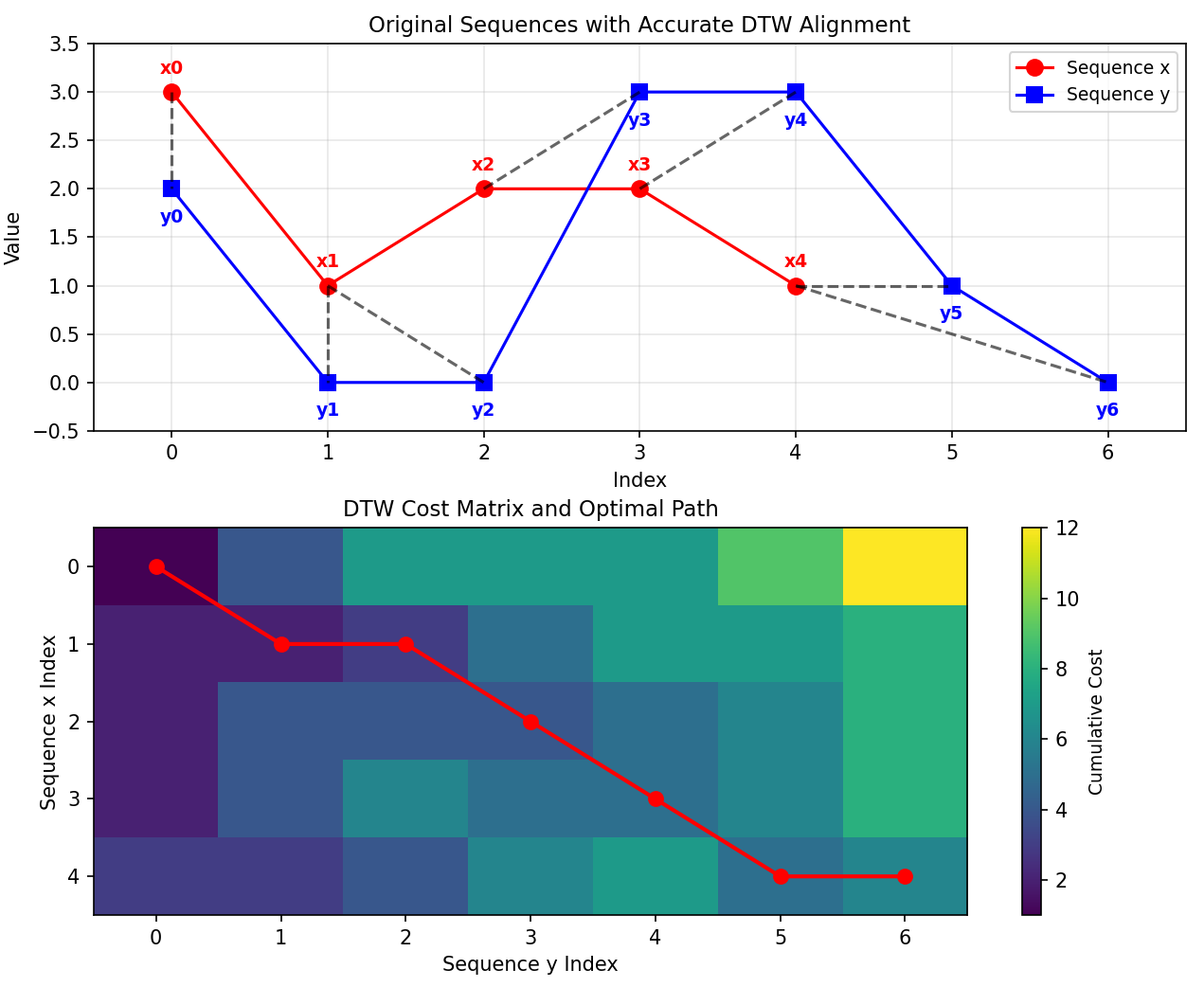
- 最优对齐路径:从 C [ m ] [ n ] C[m][n] C[m][n]反向回溯到 C [ 0 ] [ 0 ] C[0][0] C[0][0],每次选择递推时的最小前驱方向(上/左/左上),将回溯到的位置转换为原始序列的索引对 ( i , j ) (i,j) (i,j),即为两个序列的最优弹性对齐路径(路径 { ( 0 , 0 ) , ( 1 , 1 ) , ( 1 , 2 ) , ( 2 , 3 ) , ( 3 , 4 ) , ( 4 , 5 ) , ( 4 , 6 ) } \{(0,0),(1,1),(1,2),(2,3),(3,4),(4,5),(4,6)\} {(0,0),(1,1),(1,2),(2,3),(3,4),(4,5),(4,6)})。
提取路径中每个点的局部距离 D [ i ] [ j ] D[i][j] D[i][j]
从局部距离矩阵中精准提取路径每个位置的数值,一一对应:
| 最优路径点 ( i , j ) (i,j) (i,j) | 对应局部距离 D [ i ] [ j ] = ∣ x i − y j ∣ D[i][j] = \lvert x_i - y_j \rvert D[i][j]=∣xi−yj∣ | 计算过程 | 结果 |
|---|---|---|---|
| (0,0) | D [ 0 ] [ 0 ] D[0][0] D[0][0] | ∣ 3 − 2 ∣ \lvert3-2\rvert ∣3−2∣ | 1 |
| (1,1) | D [ 1 ] [ 1 ] D[1][1] D[1][1] | ∣ 1 − 0 ∣ \lvert1-0\rvert ∣1−0∣ | 1 |
| (1,2) | D [ 1 ] [ 2 ] D[1][2] D[1][2] | ∣ 1 − 0 ∣ \lvert1-0\rvert ∣1−0∣ | 1 |
| (2,3) | D [ 2 ] [ 3 ] D[2][3] D[2][3] | ∣ 2 − 3 ∣ \lvert2-3\rvert ∣2−3∣ | 1 |
| (3,4) | D [ 3 ] [ 4 ] D[3][4] D[3][4] | ∣ 2 − 3 ∣ \lvert2-3\rvert ∣2−3∣ | 1 |
| (4,5) | D [ 4 ] [ 5 ] D[4][5] D[4][5] | ∣ 1 − 1 ∣ \lvert1-1\rvert ∣1−1∣ | 0 |
| (4,6) | D [ 4 ] [ 6 ] D[4][6] D[4][6] | ∣ 1 − 0 ∣ \lvert1-0\rvert ∣1−0∣ | 1 |
| 合计 | --- | --- | 6 |
累加所有局部距离
将上述结果求和,就是最终的DTW距离:
1 + 1 + 1 + 1 + 1 + 0 + 1 = 6 1+1+1+1+1+0+1 = \boldsymbol{6} 1+1+1+1+1+0+1=6