📊 现值(PV)与净现值(NPV)详解
------基于银行存款场景的通俗解析
适用对象 :信息系统项目管理师(软考高项)考生、项目经理、投资决策人员
核心目标:理解货币时间价值,掌握NPV计算与应用
一、为什么需要"折现"?------货币的时间价值
💡 核心理念:
今天的1元钱 ≠ 明天的1元钱。
因为:
- 钱可以投资生息(如存银行);
- 未来存在不确定性(通货膨胀、风险等)。
✅ 现实对应:
- 折现率(Discount Rate) = 银行年利率 (或你的最低期望回报率) 例如:银行1年期定期利率为 5%,则折现率 r=5%=0.05
二、现值(Present Value, PV)
🔹 定义
现值 是指 未来某一时点的一笔资金,在当前时点的等效价值。
换句话说:为了在未来拿到 FV 元,现在需要投入多少钱?
🔹 计算公式(复利折现)
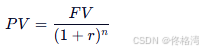
| 符号 | 含义 |
|---|---|
| PVPV | 现值(Present Value) |
| FVFV | 未来值(Future Value) |
| rr | 折现率(如 5% → 0.05) |
| nn | 时间(年数) |
🔸 银行示例1:1年后拿105元,现在要存多少?
- 已知: FV=105 , r=5%, n=1
- 计算:
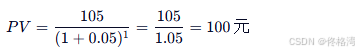
✅ 结论 :1年后的105元,今天只值100元。
🔸 银行示例2:2年后拿110.25元,现在要存多少?
- FV=110.25 , r=5% , n=2
- 计算:
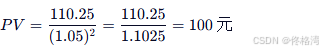
✅ 规律:时间越长,同样金额的现值越小。
三、净现值(Net Present Value, NPV)
🔹 定义
净现值 是项目 所有现金流入与流出的现值之和,用于衡量项目是否创造经济价值。
本质:比较"做这个项目" vs "把钱存银行",哪个更划算?
🔹 计算公式
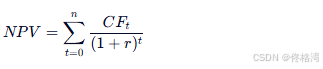
表格
| 符号 | 含义 |
|---|---|
| CFt | 第 t 年的净现金流 (收入 - 支出) (通常 CF0为负,表示初始投资) |
| rr | 折现率 |
| tt | 时间(第0年 = 当前) |
🔸 投资决策规则
表格
| NPV 结果 | 经济含义 | 决策建议 |
|---|---|---|
| NPV > 0 | 项目收益 > 存银行的收益 → 创造了额外价值 | ✅ 接受 |
| NPV = 0 | 项目收益 = 存银行收益 → 保本 | ⚠️ 可接受 |
| NPV < 0 | 项目收益 < 存银行收益 → 亏损机会成本 | ❌ 拒绝 |
🔸 银行对比案例:自动售货机项目
▶ 项目情况:

▶ 计算各年现金流的现值:
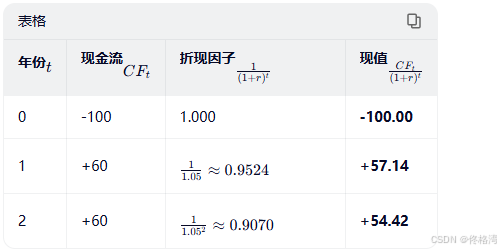
▶ 计算 NPV:
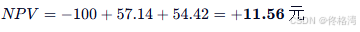
✅ 结论:
- NPV > 0,说明该项目比"把100元存银行2年"更赚钱;
- 值得投资!
🔸 对比:如果第2年只收回40元?

四、关键总结
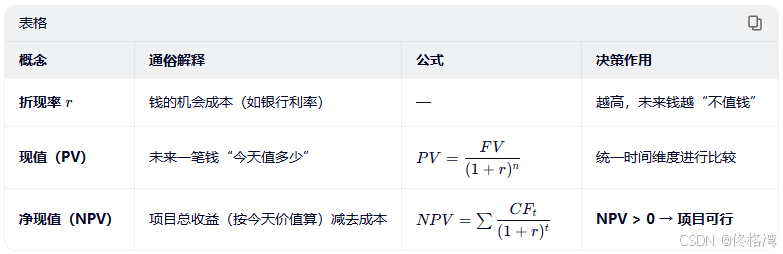
五、软考高项应用提示
- 必考公式:
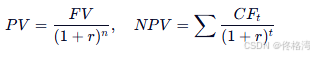
- 典型题型:

- 论文写法 : "通过净现值分析(NPV=+47万元),证明项目经济可行,成功获得立项批准。"
💡 记住一句话 :
NPV 就是把所有未来的钱,按"银行利率"换算成今天的价值,再加总。
如果结果是正的,说明你赚了"超额利润";如果是负的,不如把钱存银行!
