时、频域同步技术
为了解决频率选择性信道(或等价为多径衰落信道中的ISI)引起的失真,OFDM系统在正交子载波上并行传输消息数据。然而,只有正交性得到保持时,OFDM才能够发挥其技术优势。因此,在正交性得不到充分保证的情况下,系统性能会因ISI和ICI而下降。当存在大小为 δ \delta δ的STO和大小为 ε \varepsilon ε的CFO时,基带接收信号可以表示为:
y l [ n ] = IDFT { Y l [ k ] } = IDFT { H l [ k ] X l [ k ] + Z l [ k ] } = 1 N ∑ k = 0 N − 1 H l [ k ] X l [ k ] e j 2 π ( k + ε ) ( n + δ ) / N + z l [ n ] y_l[n]=\text{IDFT}\left\{Y_l[k]\right\}=\text{IDFT}\left\{H_l[k]X_l[k]+Z_l[k]\right\}=\frac{1}{N}\sum\limits_{k=0}^{N-1}H_l[k]X_l[k]e^{j2\pi(k+\varepsilon)(n+\delta)/N}+z_l[n] yl[n]=IDFT{Yl[k]}=IDFT{Hl[k]Xl[k]+Zl[k]}=N1k=0∑N−1Hl[k]Xl[k]ej2π(k+ε)(n+δ)/N+zl[n]
其中, z l [ n ] = IDFT { Z l [ k ] } z_l[n]=\text{IDFT}\left\{Z_l[k]\right\} zl[n]=IDFT{Zl[k]}。
STO的影响
在OFDM系统中,IFFT和FFT分别是发射机调制和接收机解调的基本功能。为了在接收机进行 N N N点FFT,需要在OFDM符号周期内得到对发射信号的精确采样。换句话说,为了检测每一个(去CP后的)OFDM符号的起始点,必须执行符号定时同步步,这样有助于获得精确的采样。

上表显示了具有 δ \delta δ个采样的STO如何在时域和频域影响接收符号,其中为了叙述简便,忽略了信道和噪声的影响。从上表中可以看出,时域上 δ \delta δ大小的STO会引起频域上 2 π δ / N 2\pi \delta/N 2πδ/N大小的相位偏差,相位偏差与子载波编号 k k k和 δ \delta δ成比例。
根据对OFDM符号起始点估计的位置不同,STO具有不同的影响。下图显示了四中不同情况下的定时偏差,即与精确的定时时刻相比,估计的起始点分别为准确、早一点、更早一点和稍晚一点。此处,假设多径时延扩展为 τ max \tau_{\text{max}} τmax,并且在后面的分析汇总,忽略信道和噪声的影响。
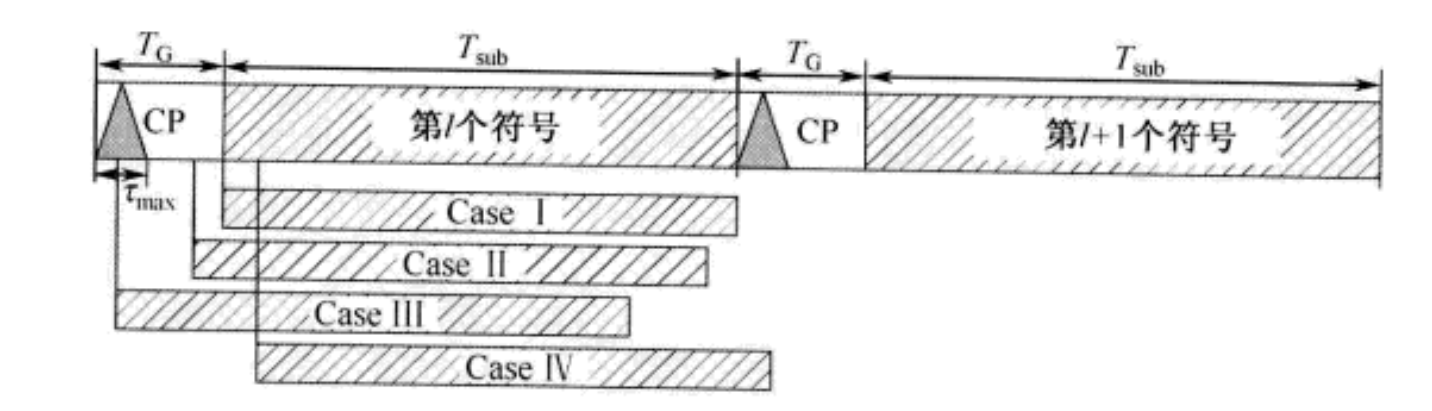
- Case 1:估计的OFDM符号起始点与精确的定时一致,因此能够保持子载波频率分量之间的正交性。在这种情况下,可以完美地恢复OFDM符号,而且没有任何干扰;
- Case 2:估计的OFDM符号起始点在精确的定时点之前,但处在前一个OFDM符号信道响应的末端之后。在这种情况下,低 l l l个符号与第 l − 1 l-1 l−1个符号不会重叠,即不存在有前一个符号引起的ISI。为了观察STO的影响,这里考虑频域接收信号。对时域接收信号的采样 { x l [ n + δ ] } n = 0 N − 1 \left\{x_l[n+\delta]\right\}_{n=0}^{N-1} {xl[n+δ]}n=0N−1进行FFT,得到频域接收信号:
Y l [ k ] = 1 N ∑ n = 0 N − 1 x l [ n + δ ] e − j 2 π n k / N = 1 N ∑ n = 0 N − 1 { ∑ p = 0 N − 1 X l [ p ] e j 2 π ( n + δ ) p / N } e − j 2 π n k / N = 1 N ∑ p = 0 N − 1 X l [ p ] e j 2 π δ p / N ∑ n = 0 N − 1 e j 2 π ( p − k ) n / N = X l [ k ] e j 2 π k δ / N Y_l[k]=\frac{1}{N}\sum\limits_{n=0}^{N-1}x_l[n+\delta]e^{-j2\pi nk/N}=\frac{1}{N}\sum\limits_{n=0}^{N-1}\left\{\sum\limits_{p=0}^{N-1}X_l[p]e^{j2\pi (n+\delta)p/N}\right\}e^{-j2\pi nk/N}=\frac{1}{N}\sum\limits_{p=0}^{N-1}X_l[p]e^{j2\pi \delta p/N}\sum\limits_{n=0}^{N-1}e^{j2\pi (p-k)n/N}=X_l[k]e^{j2\pi k\delta / N} Yl[k]=N1n=0∑N−1xl[n+δ]e−j2πnk/N=N1n=0∑N−1{p=0∑N−1Xl[p]ej2π(n+δ)p/N}e−j2πnk/N=N1p=0∑N−1Xl[p]ej2πδp/Nn=0∑N−1ej2π(p−k)n/N=Xl[k]ej2πkδ/N
∑ n = 0 N − 1 e j 2 π p − k N n = e j 2 π ( p − k ) N − 1 N ⋅ sin [ π ( k − p ) ] sin [ π ( k − p ) / N ] = { N , k = p 0 , k ≠ p \sum\limits_{n=0}^{N-1}e^{j2\pi \frac{p-k}{N}n}=e^{j2\pi(p-k)\frac{N-1}{N}}\cdot \frac{\sin[\pi(k-p)]}{\sin[\pi (k-p)/N]}=\left\{\begin{matrix} N,k=p\\ 0,k\ne p \end{matrix}\right. n=0∑N−1ej2πNp−kn=ej2π(p−k)NN−1⋅sin[π(k−p)/N]sin[π(k−p)]={N,k=p0,k=p
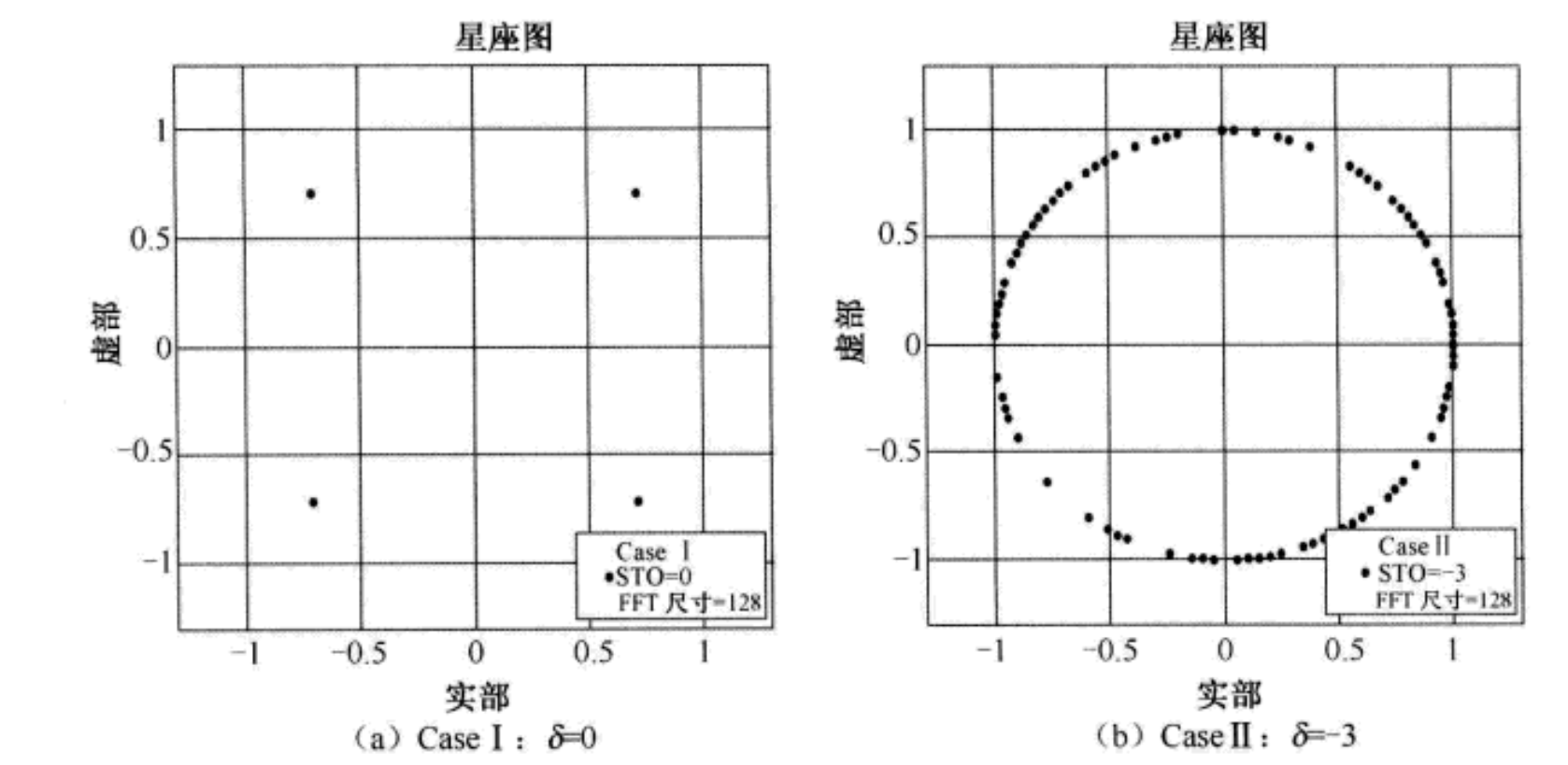
上式表明,可以完全保持子载波频率分量间的正交性。然而,从上式也可以看出,接收信号中存在相位偏差,它使信号的星座绕原点旋转,其中相位偏与 δ \delta δ和 k k k成正比。下图(a)和(b)分别显示了Case 1和Case 2中接收信号的星座图。正如期望的那样,在Case 2中观察到了由STO造成的相位偏差现象。通过一个单抽头的频域均衡器,可以直接补偿相位偏差。
- Case 3:估计的OFDM符号起始点早于前一个OFDM符号信道响应的末端,因此符号定时太早而无法避免ISI。这种情况下,子载波间的正交性被(来自前一个符号的)ISI破坏,同时出现了ICI;
- Case 4:估计的OFDM符号起始点滞后于精确的定时点。在这种情况下,在FFT间隔 T s u b T_{sub} Tsub内,信号由当前的OFDM符号 x l [ n ] x_l[n] xl[n]的一部分和下一个OFDM符号 x l + 1 [ n ] x_{l+1}[n] xl+1[n]的一部分组成。在FFT间隔内,接收信号可以表示为:
y l [ n ] = { x l [ n + δ ] , 0 ≤ n ≤ N − 1 − δ x l + 1 [ n + 2 δ − N G ] , N − δ ≤ n ≤ N − 1 y_l[n]=\left\{\begin{matrix} x_l[n+\delta],0\le n \le N-1-\delta\\ x_{l+1}[n+2\delta -N_G],N-\delta \le n \le N-1 \end{matrix}\right. yl[n]={xl[n+δ],0≤n≤N−1−δxl+1[n+2δ−NG],N−δ≤n≤N−1
其中, N G N_G NG为GI的长度。对复数信号 { y l [ n ] } n = 0 N − 1 \left\{y_l[n]\right\}_{n=0}^{N-1} {yl[n]}n=0N−1进行FFT变换,得到解调信号:

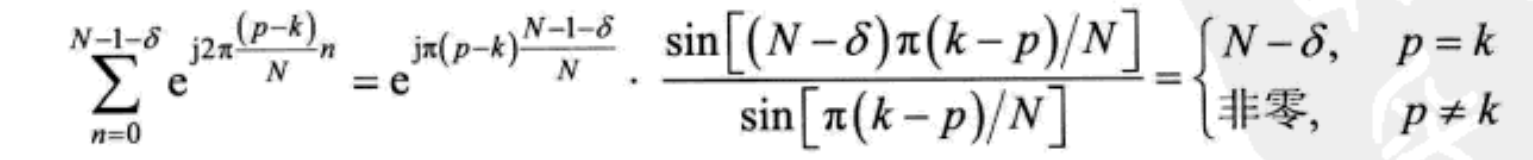
上式中最后一行的第二项对应于ICI,这意味着正交性已经被破坏。此外,从上式中最后一行可以清楚地看到,接收信号中存在来自下一个OFDM符号 X l + 1 [ p ] X_{l+1}[p] Xl+1[p]的ISI。
下图(a)和(b)分别显示了Case 3和Case 4的信号星座图。在Case 4中,失真(包括相位偏差)过于严重,以至于无法得到补偿。这说明为了防止出现这种情况下的STO,符号定时方案是必要的。
CFO的影响
通过载波调制将基带信号向上变换到通频带,然后,在接收机通过使用具有相同频率的本地载波将信号向下变换到基带。总的来说,与载波信号相关的畸变有有两种。一种是由发射机和接收机的载波信号发生器不稳定引起的相位噪声 ,可以将其建模为一个零均值的维纳随机过程。另一种是由多普勒频移 f d f_d fd所引起的CFO 。尽管我们想要在发射机和接收机产生相同频率的载波,但是载波频率会因振荡器固有的物理特性不同而难以保持一致。令 f c f_c fc和 f c ′ f_c' fc′分别表示发射机和接收机的载波频率; f o f f s e t f_{offset} foffset表示二者之间的差值,即 f o f f s e t = f c − f c ′ f_{offset}=f_c-f_c' foffset=fc−fc′。多普勒频移 f d f_d fd由载波频率 f c f_c fc和移动终端的速度 v v v共同决定:
f d = v ⋅ f c c f_d=\frac{v\cdot f_c}{c} fd=cv⋅fc
其中, c c c为光速。定义归一化的CFO为CFO与子载波间隔的比值:
ε = f o f f s e t △ f \varepsilon=\frac{f_{offset}}{\triangle f} ε=△ffoffset
令 ε i \varepsilon_i εi和 ε f \varepsilon_f εf分别表示 ε \varepsilon ε的整数部分和小数部分,即 ε = ε i + ε f \varepsilon=\varepsilon_i+\varepsilon_f ε=εi+εf,其中 ε i = ⌊ ε ⌋ \varepsilon_i=\lfloor \varepsilon \rfloor εi=⌊ε⌋。下表给出了不同商业系统中的多普勒频率和归一化CFO,其中MS的速度为120km/h,且相位偏差与 ε \varepsilon ε和 n n n成正比。这相当于在频域信号 X [ k ] X[k] X[k]上产生了一个 − ε -\varepsilon −ε的频差。
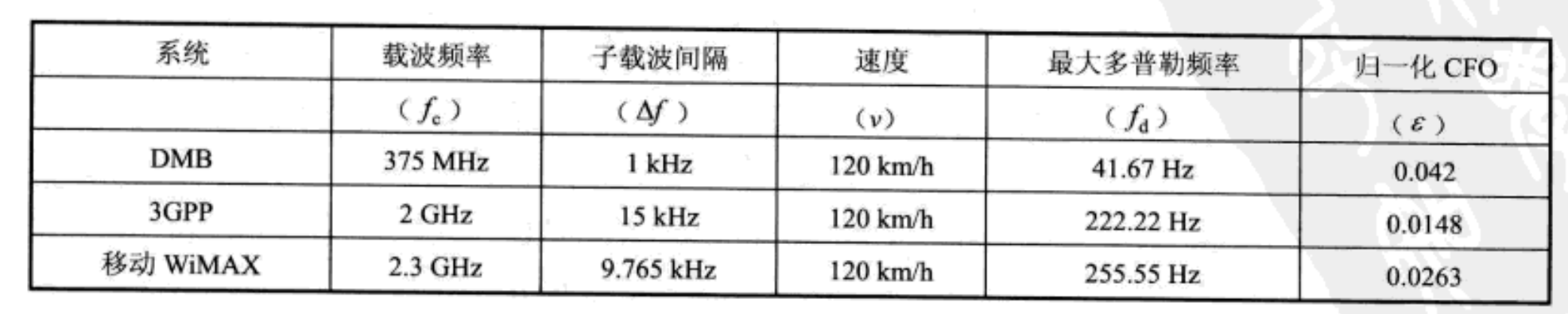
对于发射信号 x [ n ] x[n] x[n],下表总结了CFO对接收信号 y [ n ] y[n] y[n]的影响。

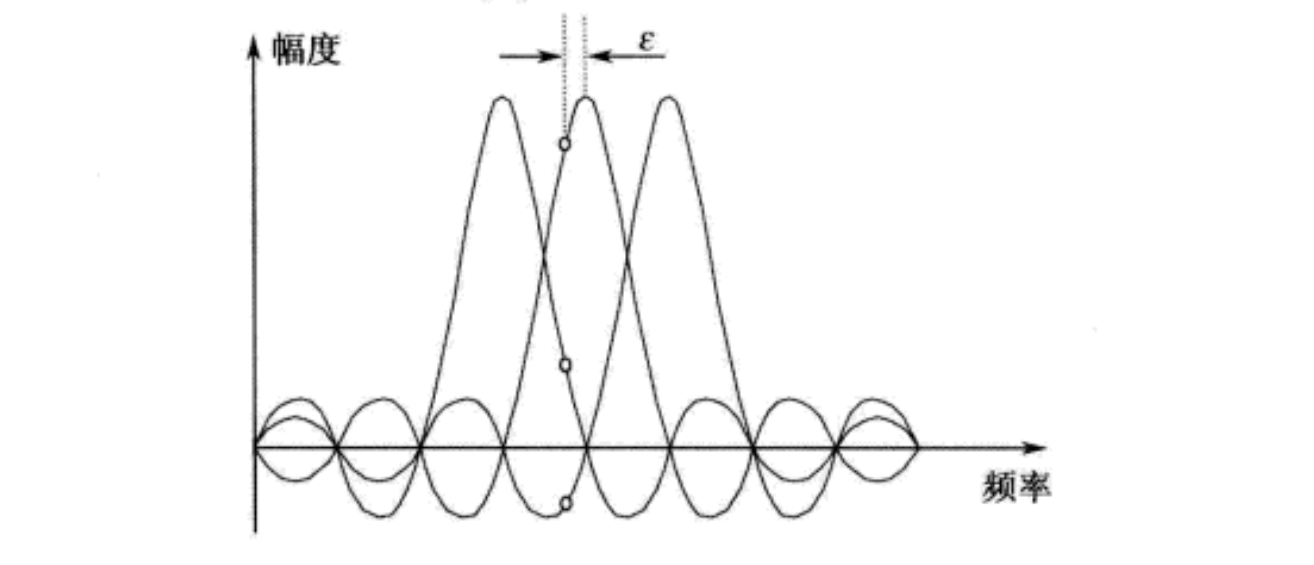
下图显示了CFO对频域信号 X [ k ] X[k] X[k]的影响。大小为 ε \varepsilon ε的CFO使 X [ k ] X[k] X[k]产生了 − ε -\varepsilon −ε的频差,并且导致了ICI,这说明子载波分量收到了其他子载波分量的影响。为了观察CFO的影响,假设发射机和接收机之间仅存在 ε \varepsilon ε大小的CFO,没有任何相位噪声。可得,时域接收信号可以表示为:
y l [ n ] = 1 N ∑ k = 0 N − 1 H l [ k ] X l [ k ] e j 2 π ( k + ε ) / N + z l [ n ] y_l[n]=\frac{1}{N}\sum\limits_{k=0}^{N-1}H_l[k]X_l[k]e^{j2\pi(k+\varepsilon)/N}+z_l[n] yl[n]=N1k=0∑N−1Hl[k]Xl[k]ej2π(k+ε)/N+zl[n]
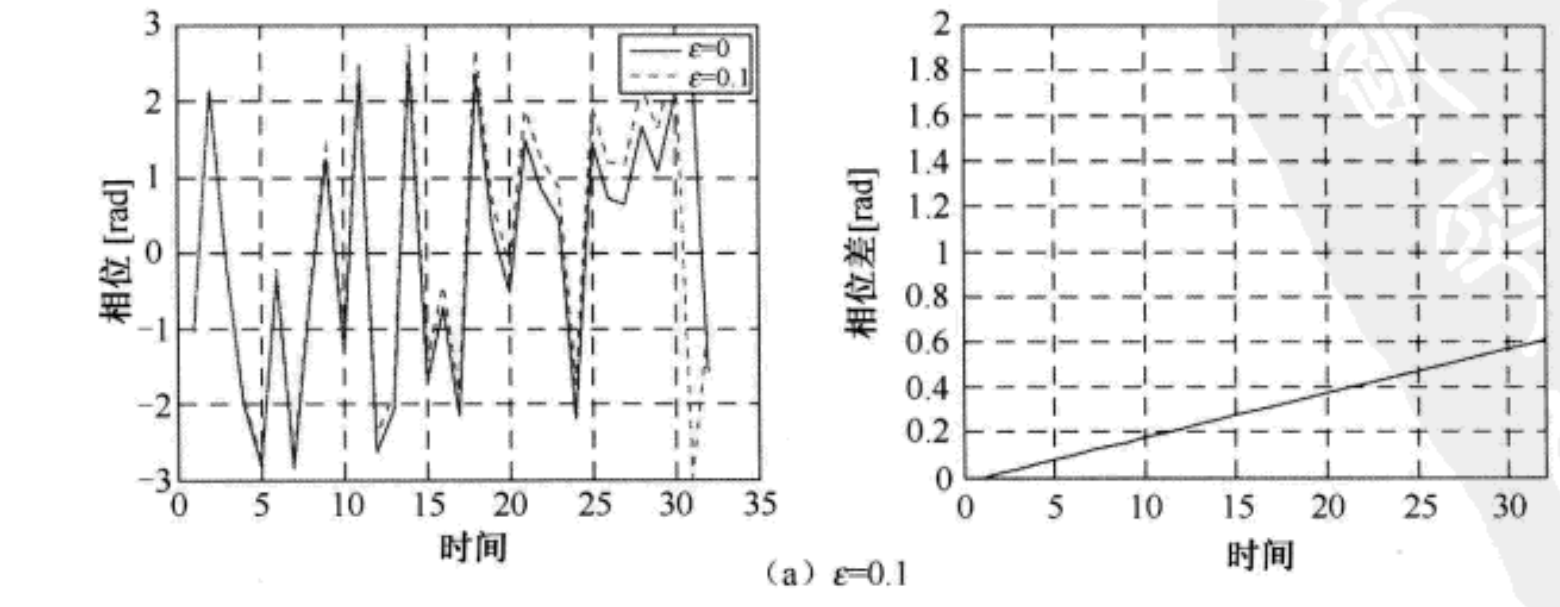
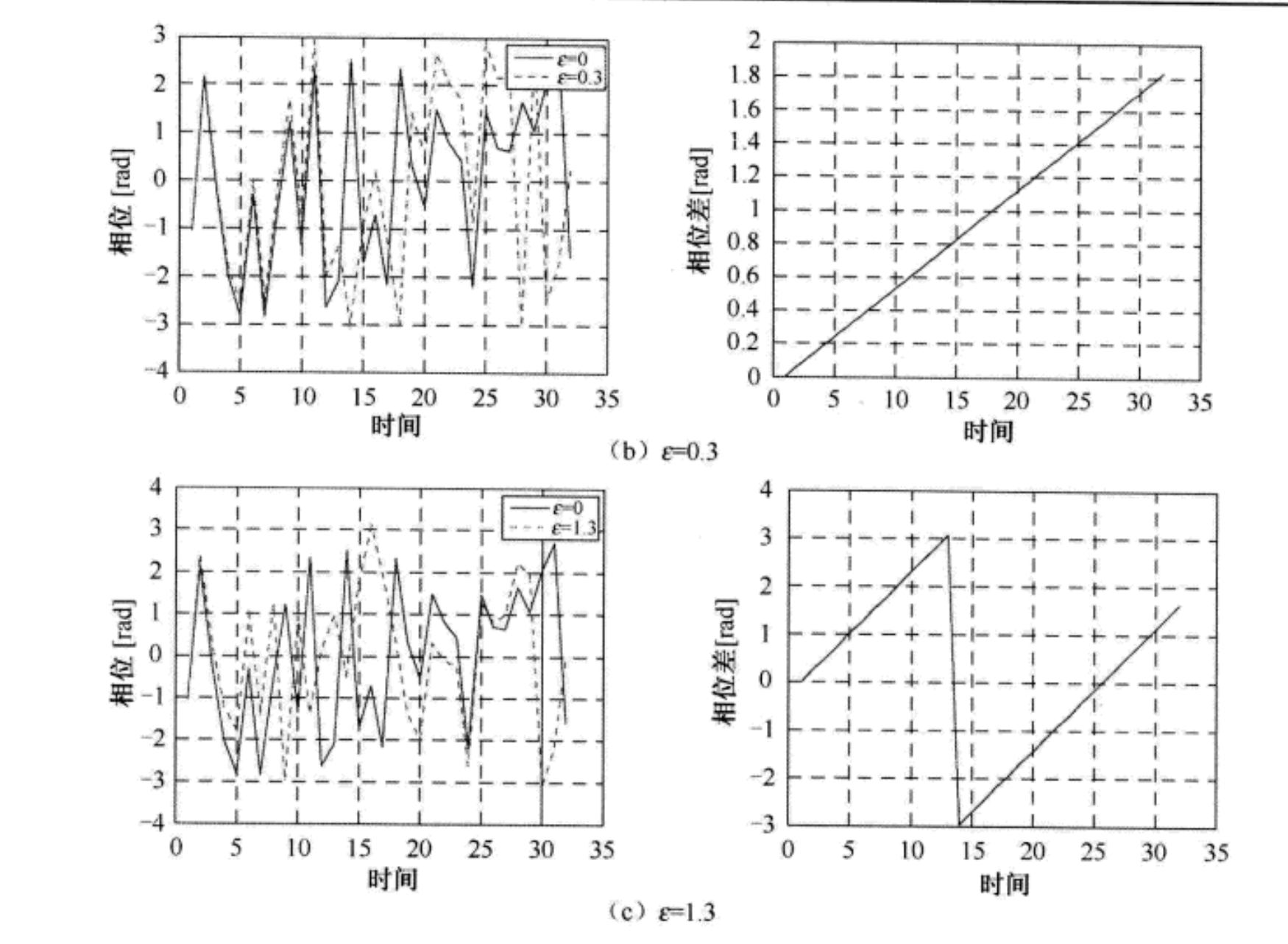
下图(a)、(b)和(c)分别显示了不同大小的CFO对时域信号相位的影响,这些影响也可以由上表或者上式预测得到。此处,假设FFT的大小为 N = 32 N=32 N=32,采用没有噪声影响的QPSK调制。在左侧的图中,实线和虚线分别表示没有CFO的理想情况(即 ε = 0 \varepsilon=0 ε=0)和存在CFO的情况(即 ε ≠ 0 \varepsilon \ne 0 ε=0)。在右侧的图中显示了它们的相位差。从这些图中可以看到,当CFO增大时接收信号在时域快速交替。相位差随时间的增加而线性增加,相伴立差的斜率随CFO的增大而增大。如下图(c)所示,如果 ε > 0.5 ε>0.5 ε>0.5,那么在一个OFDM符号时间内的相位差将超过 π π π,结果会引起相位模糊。相位模糊与CFO的估计范围有关,归一化的CFO可以分解成两部分: 整数载波频率偏差(IntegerCarrier FrequencyOffset,IFO) ε i ε_i εi 和 小数载波频率偏差(Fractional Carrier Freequency Offset, FFO) ε f ε_f εf ,即 ε = ε i + ε f ε=ε_i+ε_f ε=εi+εf。
IFO的影响
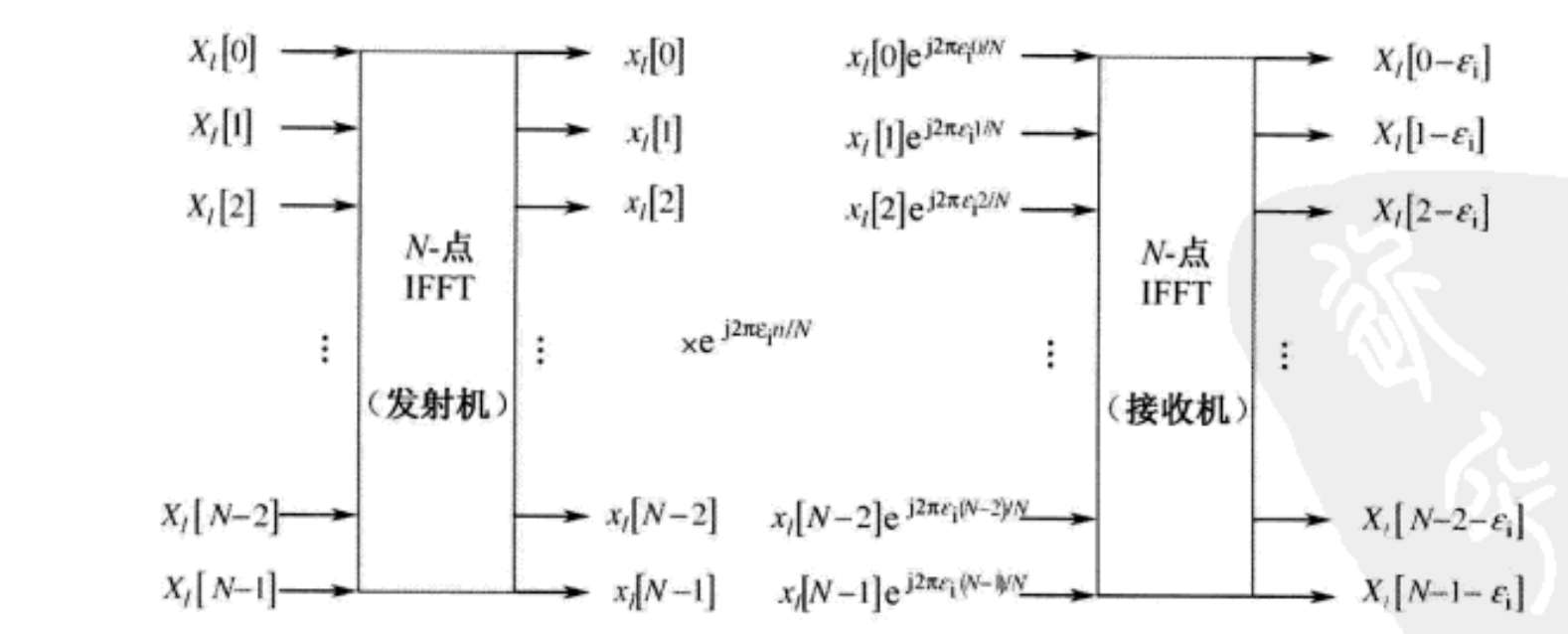
下图说明了发射采样 { x l [ n ] } n = 0 N − 1 \left\{x_l[n]\right\}_{n=0}^{N-1} {xl[n]}n=0N−1如何经历大小为 ε i \varepsilon_i εi的IFO。在接收机,大小为 ε i \varepsilon_i εi的IFO使得接收信号为KaTeX parse error: Undefined control sequence: \varepsiloi at position 10: e^{j2\pi \̲v̲a̲r̲e̲p̲s̲i̲l̲o̲i̲ ̲n/N}x[n]。由于IFO的作用,发射信号 X [ k ] X[k] X[k]在接收机被循环移位 ε i \varepsilon_i εi,因此在第 k k k个子载波上的接收信号为 X [ k − ε i ] X[k-\varepsilon_i] X[k−εi]。除非能够补偿循环移位,否则循环移位会导致BER性能的显著下降。然而,子载波频率分量之间的正交性没有被破坏,因此没有出现ICI。
FFO的影响
y l [ n ] = 1 N ∑ k = 0 N − 1 H l [ k ] X l [ k ] e j 2 π ( k + ε ) / N + z l [ n ] y_l[n]=\frac{1}{N}\sum\limits_{k=0}^{N-1}H_l[k]X_l[k]e^{j2\pi(k+\varepsilon)/N}+z_l[n] yl[n]=N1k=0∑N−1Hl[k]Xl[k]ej2π(k+ε)/N+zl[n]
上式中的 { y l [ n ] } \left\{ y_l[n] \right\} {yl[n]}进行FFT,那么存在大小为 ε f \varepsilon_f εf的FFO的频域接收信号可以表示为:

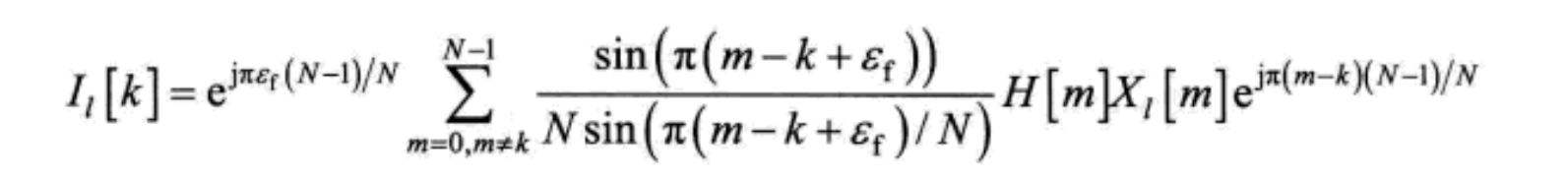
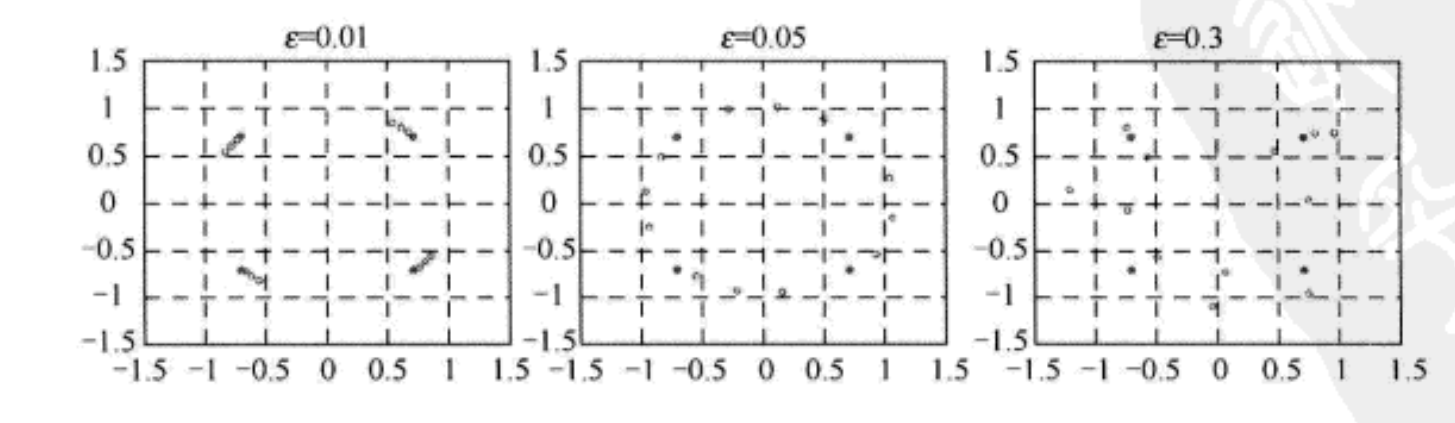
上式中的最后一行的第一项表示由FFO引起的第 k k k个子载波频率分量的幅度失真和相位失真。同时,上式中的 I l [ k ] I_l[k] Il[k]表示其他子载波对第 k k k个子载波的ICI。这意味着由于存在FFO,子载波之间的正交性将无法保持。下图显示了在不同FFO的情况下的三个连续的OFDM信号,其中忽略信道、STO和噪声影响。从下图可以看出,当FFO增大时,幅度和相位失真变得更加严重了,这主要归因于上式中的ICI项。
STO估计技术
在OFDM系统中,STO不仅能引起相位失真(通过均衡器进行补偿),而且能引起ISI(一旦发声,就无法被修正)。因此,为了保证OFDM系统性能,在接收机必须利用同步技术来估计STO,以便能够准确估计出OFDM符号的起始点。
时域STO估计技术
考虑CP大小为 T G T_G TG( N G N_G NG个采样)、有效数据长度为 T s u b T_{sub} Tsub( N s u b N_{sub} Nsub个采样)的OFDM符号。在时域中,通过使用CP或训练符号可以估计STO。
基于CP的STO估计技术
CP是OFDM符号中一部分数据的一个副本。这就意味着CP和相应的数据部分是相同的,而这种相同之处可以用于对STO的估计。在下图中, B B B和 B ′ B' B′分别表示CP的 N G N_G NG个采样的数据部分的 N G N_G NG个采样。两个采样块相隔 N s u b N_{sub} Nsub个采样。如下图示所示,考虑两个滑动窗W1和W2,其间距为 N s u b N_{sub} Nsub个采样。通过滑动W1和W2,可以搜索两个窗内采样之间的相似度。当OFDM符号的CP落在W1内时,两个窗内的 N G N_{G} NG个采样块之间的相似度达到最大。利用这个最值点,可以识别STO。
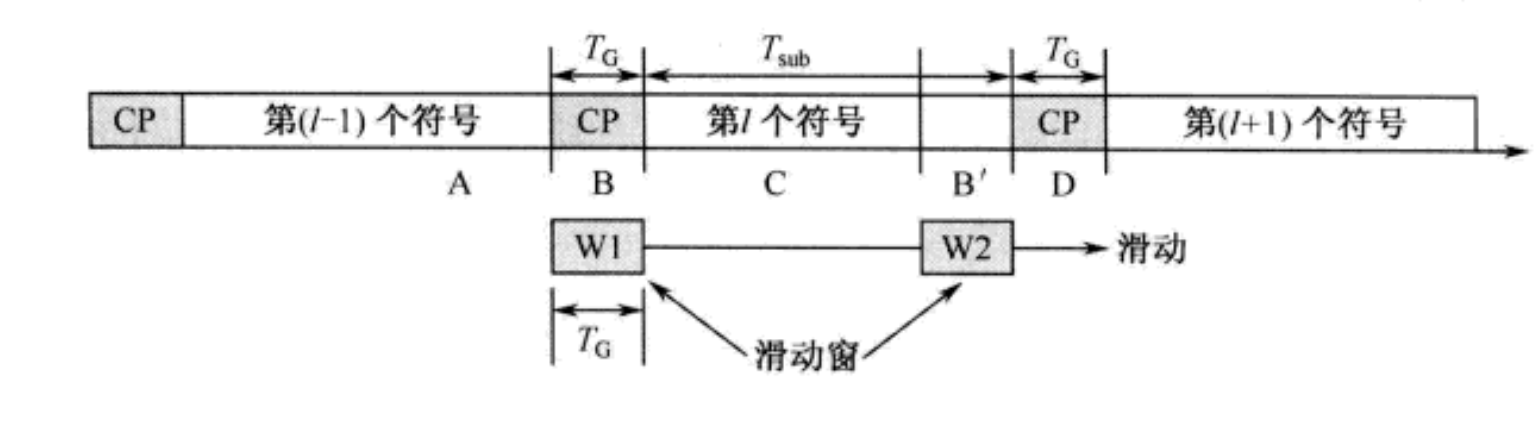
当W1和W2中两个采样块之间的差最小时,这两个块的相似度达到最大。所以,在两个窗内,通过搜索使两个块之差取最小值所在的点,就能够估计出STO:
δ ^ = arg min δ { ∑ i = δ N G − 1 + δ ∣ y l [ n + i ] − y l [ n + N + i ] ∣ } \hat\delta=\underset{\delta}{\text{arg min}}\left\{\sum\limits_{i=\delta}^{N_G-1+\delta }\begin{vmatrix} y_l[n+i]-y_l[n+N+i] \end{vmatrix}\right\} δ^=δarg min{i=δ∑NG−1+δ yl[n+i]−yl[n+N+i] }
尽管这种技术简单,但是当接收系统中存在CFO时,其性能会下降。为了处理CFO,通过最小化W1中采样块和W2中采样块之差的平方来估计STO:
δ ^ = arg min δ { ∑ i = δ N G − 1 + δ ( ∣ y l [ n + i ] − y l [ n + N + i ] ∣ ) 2 } \hat\delta=\underset{\delta}{\text{arg min}}\left\{\sum\limits_{i=\delta}^{N_G-1+\delta }(\begin{vmatrix} y_l[n+i]-y_l[n+N+i] \end{vmatrix})^2\right\} δ^=δarg min{i=δ∑NG−1+δ( yl[n+i]−yl[n+N+i] )2}
利用W1和W2中两个采样块之间的相关性,也可以估计STO,即
δ ^ = arg min δ { ∑ i = δ N G − 1 + δ ∣ y l [ n + i ] y l ∗ [ n + N + i ] ∣ } \hat\delta=\underset{\delta}{\text{arg min}}\left\{\sum\limits_{i=\delta}^{N_G-1+\delta }\begin{vmatrix} y_l[n+i]y_l^*[n+N+i] \end{vmatrix}\right\} δ^=δarg min{i=δ∑NG−1+δ yl[n+i]yl∗[n+N+i] }
上式相当于最大化W1中采样块和W2中采样块之间的相关性。然而,当接收信号中存在CFO时,上式的性能会下降。为了处理接收信号中的CFO,利用ML技术,通过最大化对数似然函数来估计STO:
δ ^ = arg min δ { ∑ i = δ N G − 1 + δ 2 ( 1 − ρ ) Re { y l [ n + i ] y l ∗ [ n + N + i ] } − ρ ∑ i = δ N G − 1 + δ ∣ y l [ n + i ] − y l [ n + N + i ] ∣ } \hat\delta=\underset{\delta}{\text{arg min}}\left\{\sum\limits_{i=\delta}^{N_G-1+\delta }2(1-\rho)\text{Re}\left\{y_l[n+i]y_l^*[n+N+i]\right\}-\rho\sum\limits_{i=\delta}^{N_G-1+\delta }\begin{vmatrix} y_l[n+i]-y_l[n+N+i] \end{vmatrix}\right\} δ^=δarg min{i=δ∑NG−1+δ2(1−ρ)Re{yl[n+i]yl∗[n+N+i]}−ρi=δ∑NG−1+δ yl[n+i]−yl[n+N+i] }
其中, ρ = S N R / ( S N R + 1 ) \rho=SNR/(SNR+1) ρ=SNR/(SNR+1)。还可以通过ML技术同时估计STO和CFO,STO被估计为:
δ ^ = arg min δ { ∣ γ [ δ ] ∣ − ρ Φ [ δ ] } \hat\delta=\underset{\delta}{\text{arg min}}\left\{\begin{vmatrix} \gamma[\delta] \end{vmatrix}-\rho\Phi[\delta]\right\} δ^=δarg min{ γ[δ] −ρΦ[δ]}
其中
γ [ m ] = ∑ n = m m + L − 1 y l [ n ] y l ∗ [ n + N ] \gamma[m]=\sum\limits_{n=m}^{m+L-1}y_l[n]y_l^*[n+N] γ[m]=n=m∑m+L−1yl[n]yl∗[n+N]
Φ [ m ] = 1 2 ∑ n = m m + L − 1 { ∣ y l [ n ] ∣ 2 + ∣ y l [ n + N ] ∣ 2 } \Phi[m]=\frac{1}{2}\sum\limits_{n=m}^{m+L-1}\left\{\begin{vmatrix} y_l[n] \end{vmatrix}^2+\begin{vmatrix} y_l[n+N] \end{vmatrix}^2\right\} Φ[m]=21n=m∑m+L−1{ yl[n] 2+ yl[n+N] 2}
其中, L L L表示在窗口内取平均的实际采样数。即使存在CFO,如果对相关函数 γ [ m ] \gamma[m] γ[m]取绝对值,上式中的STO估计也是鲁棒的。
基于训练符号的STO估计
通过发射训练符号,可以在接收机实现符号同步。与基于CP的方法相比,基于训练符号的方法存在因传输训练符号而带来的负荷问题,但是这种方法不受多径信道的影响。在估计过程中,可以使用两个相同的OFDM训练符号,也可以使用具有(不同重复周期)重复结构的单个OFDM训练符号。下图说明了具有重复结构的单个OFDM符号的例子,其中重复周期分别在 T s u b / 2 T_{sub}/2 Tsub/2和 T s u b / 4 T_{sub}/4 Tsub/4。通过在子载波之间插入零,在时域可以产生不同的重复样式。一旦发射机在OFDM符号中的两个块发送重复的训练信号,接收机通过最大化两个滑动窗内采样块之间的相似性,就可以找到STO。通过计算重复的训练信号的自相关函数,得到两个采样块之间的相似性。
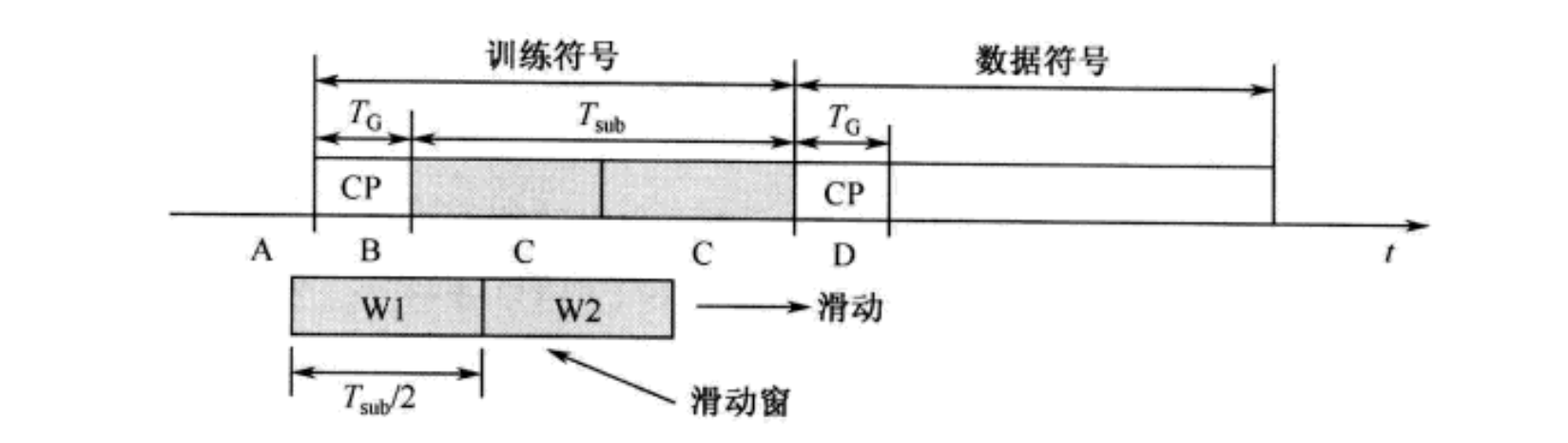
在上图中,重复周期为 T s u b / 2 T_{sub}/2 Tsub/2,接收信号的A、B和D部分与接收信号的C部分不相同。由此,可以构成两个滑动窗(W1和W2)来估计STO。与基于CP的STO估计技术一样,基于训练序列的STO估计有两种。一种时通过最小化W1和W2中两个接收采样块之间的平方得到,即:
δ ^ = arg min δ { ∑ i = δ N 2 − 1 + δ ( ∣ y l [ n + i ] − y l [ n + N + i ] ∣ ) 2 } \hat\delta=\underset{\delta}{\text{arg min}}\left\{\sum\limits_{i=\delta}^{\frac{N}{2}-1+\delta }(\begin{vmatrix} y_l[n+i]-y_l[n+N+i] \end{vmatrix})^2\right\} δ^=δarg min{i=δ∑2N−1+δ( yl[n+i]−yl[n+N+i] )2}
另一种时通过最大化似然函数得到,即
δ ^ = arg min δ { ∑ i = δ N 2 − 1 + δ ∣ y l [ n + i ] y l ∗ [ n + N 2 + i ] ∣ 2 ∣ ∑ i = δ N 2 − 1 + δ y l [ n + N 2 + i ] ∣ 2 } \hat\delta=\underset{\delta}{\text{arg min}}\left\{\frac{\sum\limits_{i=\delta}^{\frac{N}{2}-1+\delta }\begin{vmatrix} y_l[n+i]y_l^*[n+\frac{N}{2}+i] \end{vmatrix}^2}{\begin{vmatrix} \sum\limits_{i=\delta}^{\frac{N}{2}-1+\delta }y_l[n+\frac{N}{2}+i] \end{vmatrix}^2}\right\} δ^=δarg min⎩ ⎨ ⎧ i=δ∑2N−1+δyl[n+2N+i] 2i=δ∑2N−1+δ yl[n+i]yl∗[n+2N+i] 2⎭ ⎬ ⎫
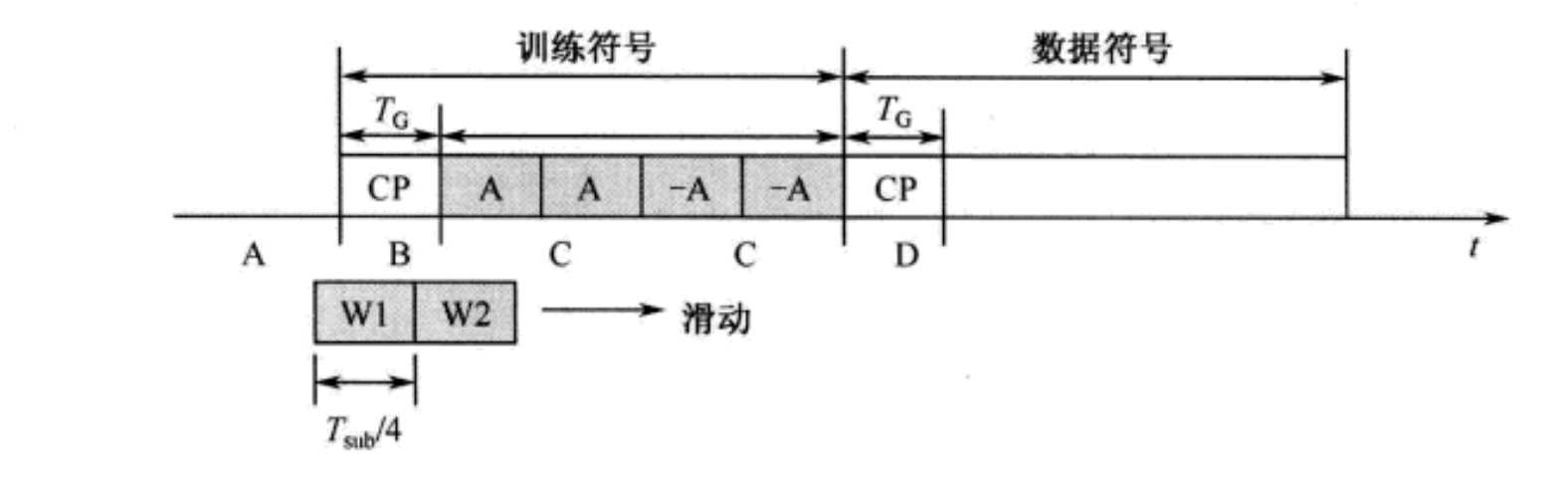
如上图所示,通过改变训练符号重复样式的周期,能够改善STO估计精度。在上图中,训练符号重复了四次,并且在第三和第四周期中对寻来你符号取反。通过下士可以进一步提高STO的估计精度:
δ ^ = arg min δ { ∑ m = 0 1 ∑ i = δ N 4 − 1 + δ ∣ y l [ n + i + N 2 m ] y l ∗ [ n + i + N 4 + N 2 m ] ∣ 2 ∣ ∑ m = 0 1 ∑ i = δ N 4 − 1 + δ y l [ n + i + N 4 + N 2 m ] ∣ 2 } \hat\delta=\underset{\delta}{\text{arg min}}\left\{\frac{\sum\limits_{m=0}^{1}\sum\limits_{i=\delta}^{\frac{N}{4}-1+\delta }\begin{vmatrix} y_l[n+i+\frac{N}{2}m]y_l^*[n+i+\frac{N}{4}+\frac{N}{2}m] \end{vmatrix}^2}{\begin{vmatrix} \sum\limits_{m=0}^{1}\sum\limits_{i=\delta}^{\frac{N}{4}-1+\delta }y_l[n+i+\frac{N}{4}+\frac{N}{2}m] \end{vmatrix}^2}\right\} δ^=δarg min⎩ ⎨ ⎧ m=0∑1i=δ∑4N−1+δyl[n+i+4N+2Nm] 2m=0∑1i=δ∑4N−1+δ yl[n+i+2Nm]yl∗[n+i+4N+2Nm] 2⎭ ⎬ ⎫
因为接收机已知训练符号,所以另一种技术是利用训练符号和接收信号之间的互相关性来估计STO。
频域STO估计技术
接收信号会因为STO而产生相位旋转。相位旋转与子载波的频率撤出那个正比,所以可用频域接收信号中相邻载波的相位差来估计STO。例如,如果对所有 k k k,都有 X l [ k ] = X l [ k − 1 ] , H l [ k ] = H l [ k − 1 ] = 1 X_l[k]=X_l[k-1],H_l[k]=H_l[k-1]=1 Xl[k]=Xl[k−1],Hl[k]=Hl[k−1]=1,那么 Y l [ k ] Y l ∗ [ k − 1 ] ≈ ∣ X l [ k ] ∣ 2 e j 2 π δ / N Y_l[k]Y_l^*[k-1]\approx \begin{vmatrix} X_l[k]\end{vmatrix}^2e^{j2\pi \delta/N} Yl[k]Yl∗[k−1]≈ Xl[k] 2ej2πδ/N,因此可以估计STO:
δ ^ = N 2 π arg ( ∑ k = 1 N − 1 Y l [ k ] Y l ∗ [ k − 1 ] ) \hat\delta=\frac{N}{2\pi}\text{arg}(\sum\limits_{k=1}^{N-1}Y_l[k]Y_l^*[k-1]) δ^=2πNarg(k=1∑N−1Yl[k]Yl∗[k−1])

如上图是一种利用相位旋转的影响进行STO估计的技术。将训练符号的共轭 X x ∗ [ k ] X_x^*[k] Xx∗[k]和存在STO的接收符号相乘,得到(延迟的)信道脉冲响应,然后从中估计出STO:
δ ^ = arg min δ ( y l x [ n ] ) \hat\delta=\underset{\delta}{\text{arg min}}(y_l^x[n]) δ^=δarg min(ylx[n])
其中,
y l x [ n ] = IFFT { Y l [ k ] e j 2 π k n / N X l ∗ [ k ] } = 1 N ∑ k = 0 N − 1 Y l [ k ] e j 2 π k n / N X l ∗ [ k ] e j 2 π k δ / N = 1 N ∑ k = 0 N − 1 Y l [ k ] X l ∗ [ k ] e j 2 π k ( n + δ ) / N = 1 N ∑ k = 0 N − 1 H l [ k ] X l [ k ] X l ∗ [ k ] e j 2 π k ( n + δ ) / N = 1 N ∑ k = 0 N − 1 H l [ k ] e j 2 π k ( n + δ ) / N = h l [ n + δ ] y_l^x[n]=\text{IFFT}\left\{Y_l[k]e^{j2\pi kn/N}X_l^*[k]\right\}=\frac{1}{N}\sum\limits_{k=0}^{N-1}Y_l[k]e^{j2\pi kn/N}X_l^*[k]e^{j2\pi k\delta/N}=\frac{1}{N}\sum\limits_{k=0}^{N-1}Y_l[k]X_l^*[k]e^{j2\pi k(n+\delta)/N}=\frac{1}{N}\sum\limits_{k=0}^{N-1}H_l[k]X_l[k]X_l^*[k]e^{j2\pi k(n+\delta)/N}=\frac{1}{N}\sum\limits_{k=0}^{N-1}H_l[k]e^{j2\pi k(n+\delta)/N}=h_l[n+\delta] ylx[n]=IFFT{Yl[k]ej2πkn/NXl∗[k]}=N1k=0∑N−1Yl[k]ej2πkn/NXl∗[k]ej2πkδ/N=N1k=0∑N−1Yl[k]Xl∗[k]ej2πk(n+δ)/N=N1k=0∑N−1Hl[k]Xl[k]Xl∗[k]ej2πk(n+δ)/N=N1k=0∑N−1Hl[k]ej2πk(n+δ)/N=hl[n+δ]
在上式中,假设训练符号 X [ k ] X[k] X[k]的功率等于1,即 X l [ k ] X l ∗ [ k ] = ∣ X [ k ] ∣ 2 = 1 X_l[k]X_l^*[k]=\begin{vmatrix} X[k]\end{vmatrix}^2=1 Xl[k]Xl∗[k]= X[k] 2=1。
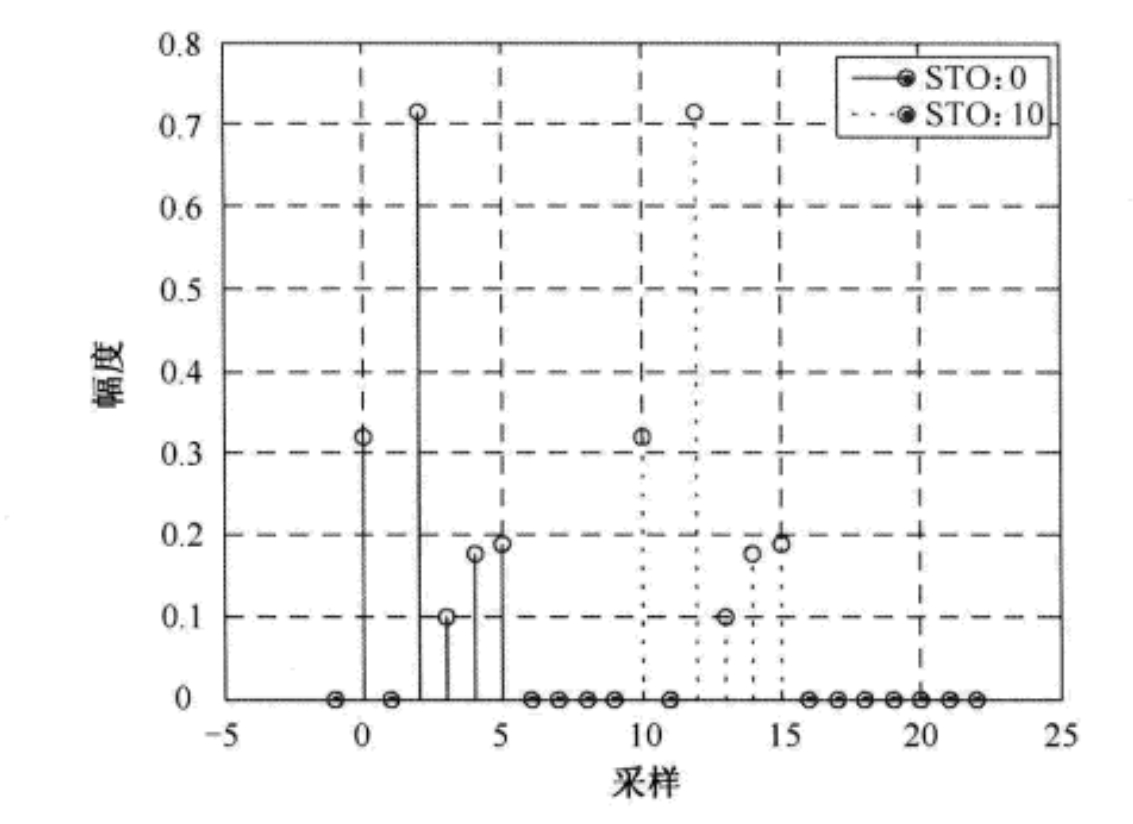
上图给出了利用信道脉冲响应进行STO估计的两个例子,其中一个 δ = 0 \delta =0 δ=0[采样],另一个 δ = 10 \delta =10 δ=10[采样]。第一个信道脉冲响应从第0个采样开始,用实线表示。第二个信道脉冲响应从第10个采样开始,用虚线表示。可以通过这种方法对STO进行正确的估计。频域STO估计技术通常会得到相当精确的估计值,所以能够用于精符号同步中。
当STO较小时,即STO小于采样间隔,根据不同的检测方案(相干和非相干)可以对STO进行不同的补偿。在利用导频符号进行相干检测的情况下,信道估计包括两方面的内容:对信道本身的估计和由STO引起的相位旋转的估计。只要STO很小,用于补偿信道影响的频域均衡器就能吸收STO的影响,所以不需要单独得到符号同步器。然而,在非相干检测的情况下,可以录用接收信号子载波间的相位差检测发射符号。因为STO会导致相位旋转,且相位旋转与子载波的频率成正比,所以在符号检测前应该通过符号同步器消除STO的影响。
CFO估计技术
与STO估计技术一样,可以在时域或频域估计CFO。
时域CFO估计技术
通常利用CP或者训练符号进行时域CFO估计。
基于CP的CFO估计技术
当符号同步完美时,大小为 ε \varepsilon ε的CFO会引起接收信号 2 π n ε / N 2\pi n\varepsilon/N 2πnε/N大小的相位旋转。因此,在假设信道影响可以忽略不计的情况下,CFO会引起CP和相应的OFDM符号后部(相隔 N N N个采样点)之间存在大小为 2 π N ε / N = 2 π ε 2\pi N\varepsilon/N=2\pi \varepsilon 2πNε/N=2πε的相位差。然后,可以根据二者相乘之后的相角找出CFO,如 ε ^ = ( 1 / 2 π ) arg { y l ∗ [ n ] y l [ n + N ] } , n = − 1 , − 1 , . . . , − N G \hat\varepsilon=(1/2\pi)\text{arg}\left\{y_l^*[n]y_l[n+N]\right\},n=-1,-1,...,-N_G ε^=(1/2π)arg{yl∗[n]yl[n+N]},n=−1,−1,...,−NG。其中 arg(z) \text{arg(z)} arg(z)表示 z z z辐角主值。为了减小噪声的影响,可以对一个CP间隔内的采样取平均:
ε ^ = 1 2 π arg { ∑ n = − N G − 1 y l ∗ [ n ] y l [ n + N ] } \hat\varepsilon=\frac{1}{2\pi}\text{arg}\left\{\sum\limits_{n=-N_G}^{-1}y_l^*[n]y_l[n+N]\right\} ε^=2π1arg{n=−NG∑−1yl∗[n]yl[n+N]}
由于用 tan − 1 ( ) \tan^{-1}() tan−1()来实现 arg ( ) \text{arg}() arg(),所以上式中CFO估计的范围是 [ − π , + π ) / 2 π = [ − 0.5 , + 0.5 ) [-\pi,+\pi)/2\pi=[-0.5,+0.5) [−π,+π)/2π=[−0.5,+0.5),从而 ∣ ε ^ ∣ < 0.5 \begin{vmatrix}\hat\varepsilon\end{vmatrix}\lt 0.5 ε^ <0.5,因此这种技术不能用于估计整数CFO。
只有频率偏差为零时, y l ∗ [ n ] y l [ n + N ] y_l^*[n]y_l[n+N] yl∗[n]yl[n+N]才为实数。这说明只要存在CFO, y l ∗ [ n ] y l [ n + N ] y_l^*[n]y_l[n+N] yl∗[n]yl[n+N]就会变成虚数。事实上, y l ∗ [ n ] y l [ n + N ] y_l^*[n]y_l[n+N] yl∗[n]yl[n+N]的虚部可以用于CFO的估计。在这种情况下,定义估计误差为:
e ε = 1 L ∑ n = 1 L Im { y l ∗ [ n ] y l [ n + N ] } e_{\varepsilon}=\frac{1}{L}\sum\limits_{n=1}^{L}\text{Im}\left\{y_l^*[n]y_l[n+N]\right\} eε=L1n=1∑LIm{yl∗[n]yl[n+N]}
其中, L L L表示求平均的采样数。可以将上式中误差函数的期望近似为:
E { e ε } = σ d 2 N sin ( 2 π ε N ) ∑ k = 1 L ∣ H k ∣ 2 ≈ K ε E\left\{e_{\varepsilon}\right\}=\frac{\sigma_d^2}{N}\sin(\frac{2\pi \varepsilon}{N})\sum\limits_{k=1}^L\begin{vmatrix}H_k\end{vmatrix}^2\approx K\varepsilon E{eε}=Nσd2sin(N2πε)k=1∑L Hk 2≈Kε
基于训练符号的CFO估计技术
基于CP的估计技术只能估计出 ∣ ε ^ ∣ < 0.5 \begin{vmatrix}\hat\varepsilon\end{vmatrix}\lt 0.5 ε^ <0.5范围内的CFO。由于在同步的初始阶段CFO会很大,所以需要能够对更大范围的CFO进行估计的技术。缩小用于相关性计算所需的采样块之间的距离,能够增大CFO的估计范围 。将训练符号在更短时间内进行重复可以实现这一目的。零 D D D为OFDM符号长度与重复样式长度之比,它是一个整数。发射机在时域以重复样式 D D D发射训练符号,可以通过对频域梳状信号取IFFT得到该训练符号,频域的梳状信号为
X l [ k ] = { A m , k = D ⋅ i , i = 0 , 1 , . . . , ( N / D − 1 ) 0 , others X_l[k]=\left\{\begin{matrix}A_m,k=D\cdot i,i=0,1,...,(N/D-1) \\ 0,\text{others}\end{matrix}\right. Xl[k]={Am,k=D⋅i,i=0,1,...,(N/D−1)0,others
其中, A m A_m Am表示 M M M进制的符号, N / D N/D N/D为一个整数。当 x l [ n ] x_l[n] xl[n]和 x l [ n + N / D ] x_l[n+N/D] xl[n+N/D]相同时(即 y l ∗ [ n ] y l [ n + N / D ] = ∣ y l [ n ] ∣ 2 e j π ε y_l^*[n]y_l[n+N/D]=\begin{vmatrix}y_l[n]\end{vmatrix}^2e^{j\pi \varepsilon} yl∗[n]yl[n+N/D]= yl[n] 2ejπε),接收机能够估计的CFO为:
ε ^ = D 2 π arg { ∑ n = 0 N / D y l ∗ [ n ] y l [ n + N / D ] } \hat\varepsilon=\frac{D}{2\pi}\text{arg}\left\{\sum\limits_{n=0}^{N/D}y_l^*[n]y_l[n+N/D]\right\} ε^=2πDarg{n=0∑N/Dyl∗[n]yl[n+N/D]}
这种技术能够估计出的CFO范围是 ∣ ε ^ ∣ ≤ D / 2 \begin{vmatrix}\hat\varepsilon\end{vmatrix}\le D/2 ε^ ≤D/2,并且估计范围随着 D D D的增大而增大。注意,用于相关性计算的采样数减少到了原来的 1 / D 1/D 1/D,这将导致MSR性能下降。换句话说,以牺牲MSE性能为代价来换取估计范围的增大。
频域CFO估计技术
如果连续发射两个相同的训练符号,那么在CFO大小为 ε \varepsilon ε的情况下,相应的两个接收信号之间的关系为:
y 2 [ n ] = y 1 [ n ] e j 2 π N ε / N ↔ Y 2 [ k ] = Y 1 [ k ] e j 2 π ε y_2[n]=y_1[n]e^{j2\pi N_{\varepsilon}/N}\leftrightarrow Y_2[k]=Y_1[k]e^{j2\pi {\varepsilon}} y2[n]=y1[n]ej2πNε/N↔Y2[k]=Y1[k]ej2πε
根据上式中的关系,可以估计出CFO为:
ε ^ = 1 2 π arc tan { ∑ k = 0 N − 1 Re [ Y 1 ∗ [ k ] Y 2 [ k ] ] / ∑ k = 0 N − 1 Im [ Y 1 ∗ [ k ] Y 2 [ k ] ] } \hat\varepsilon=\frac{1}{2\pi}\text{arc}\tan\left\{\sum\limits_{k=0}^{N-1}\text{Re}[Y_1^*[k]Y_2[k]]/\sum\limits_{k=0}^{N-1}\text{Im}[Y_1^*[k]Y_2[k]]\right\} ε^=2π1arctan{k=0∑N−1Re[Y1∗[k]Y2[k]]/k=0∑N−1Im[Y1∗[k]Y2[k]]}
尽管通过上式估计出的CFO范围为 ∣ ε ^ ∣ ≤ π / 2 π = 1 / 2 \begin{vmatrix}\hat\varepsilon\end{vmatrix}\le \pi/2\pi=1/2 ε^ ≤π/2π=1/2。但是通过使用具有 D D D个重复样式的训练符号,CFO的估计范围可以增加 D D D倍。然后在非零子载波上取平均。如果在频域上取平均的非零采样点减少了,那么MSE性能将会恶化。为了计算上式,这种估计技术需要一个特定的周期(通常被称为前导周期)来提供连续的训练符号。
也可以考虑在估计CFO的同时传输数据符号。在频域插入导频,并且在每个OFDM符号中发射,这样可以跟踪CFO。下图显示了使用到信号进行CFO估计的结构图。
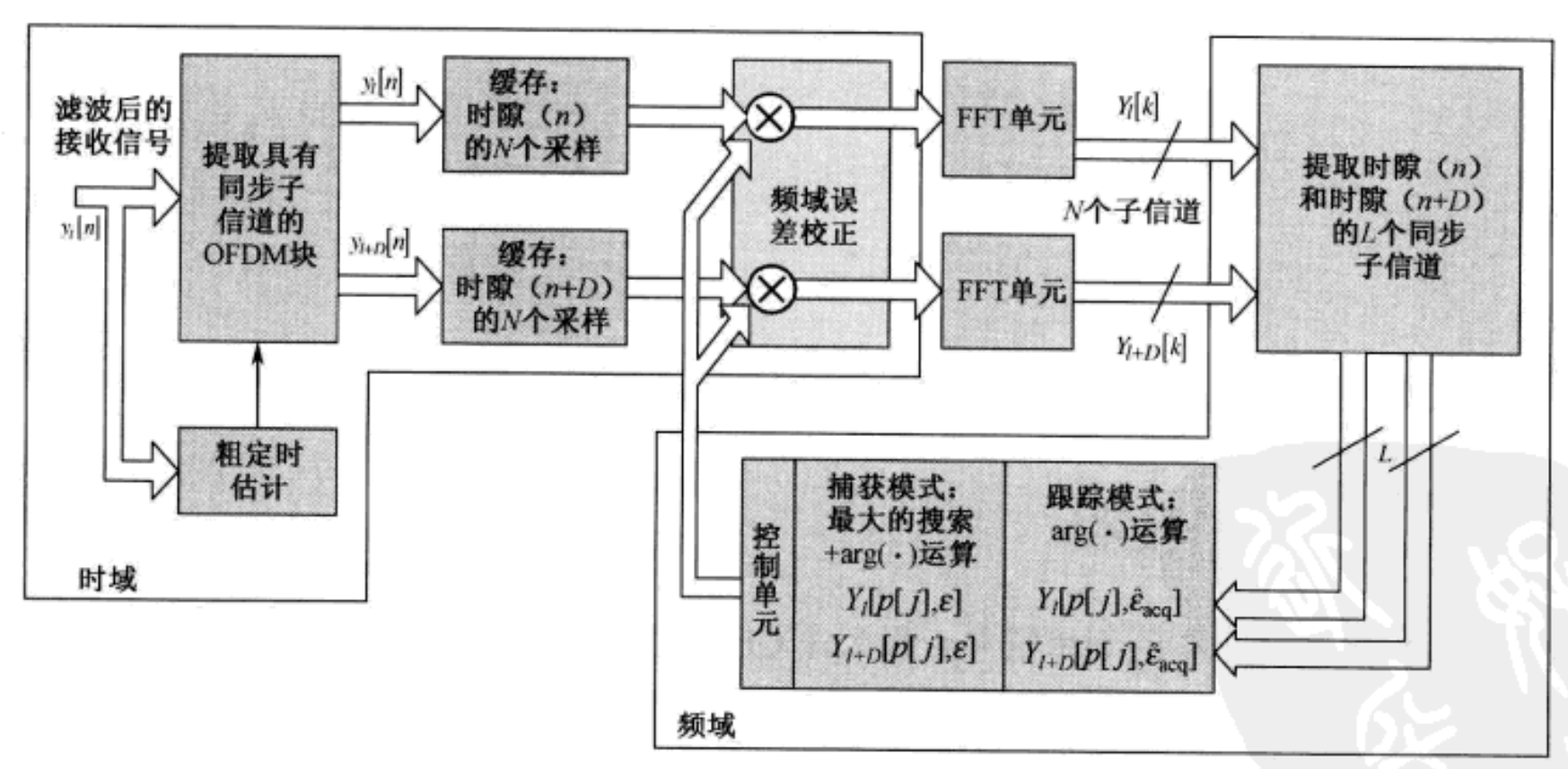
首先,在同步之后将两个OFDM符号 y l [ n ] y_l[n] yl[n]和 y l + D [ n ] y_{l+D}[n] yl+D[n]保存在存储器中,然后,通过FFT将时域信号变换成频域信号 { Y l [ k ] } k = 0 N − 1 \left\{Y_l[k]\right\}{k=0}^{N-1} {Yl[k]}k=0N−1和 { Y l + D [ k ] } k = 0 N − 1 \left\{Y{l+D}[k]\right\}_{k=0}^{N-1} {Yl+D[k]}k=0N−1,用于提取导频。最后,由频域导频估计出CFO,通过估计出的CFO在时域对接收信号进行补偿。在这个过程中,实施两种不同的CFO估计模式:捕获模式和跟踪模式。在捕获模式中,估计包括IFO在内的大范围CFO。在跟踪模式中,只进行细CFO估计。IFO估计为:
ε ^ a c q = 1 2 π ⋅ T s u b max { ∑ j = 0 L − 1 Y l + D [ p ( j ) , ε ] Y l ∗ [ p [ j ] , ε ] X l + D ∗ [ p ( j ) ] X l [ p [ j ] ] } \hat\varepsilon_{acq}=\frac{1}{2\pi\cdot T_{sub}}\text{max}\left\{\sum\limits_{j=0}^{L-1}Y_{l+D}[p(j),\varepsilon]Y_l^*[p[j],\varepsilon]X_{l+D}^*[p(j)]X_l[p[j]]\right\} ε^acq=2π⋅Tsub1max{j=0∑L−1Yl+D[p(j),ε]Yl∗[p[j],ε]Xl+D∗[p(j)]Xl[p[j]]}
其中, L , p [ j ] , X l [ p [ j ] ] L,p[j],X_l[p[j]] L,p[j],Xl[p[j]]分别表示导频个数、第 j j j个导频的位置和第 l l l个符号周期中位于 p [ j ] p[j] p[j]处的导频。同时细CFO为:
ε ^ f = 1 2 π ⋅ T s u b ⋅ D arg { ∑ j = 0 L − 1 Y l + D [ p ( j ) , ε ^ a c q ] Y l ∗ [ p [ j ] , ε ^ a c q ] X l + D ∗ [ p ( j ) ] X l [ p [ j ] ] } \hat\varepsilon_{f}=\frac{1}{2\pi\cdot T_{sub}\cdot D}\text{arg}\left\{\sum\limits_{j=0}^{L-1}Y_{l+D}[p(j),\hat\varepsilon_{acq}]Y_l^*[p[j],\hat\varepsilon_{acq}]X_{l+D}^*[p(j)]X_l[p[j]]\right\} ε^f=2π⋅Tsub⋅D1arg{j=0∑L−1Yl+D[p(j),ε^acq]Yl∗[p[j],ε^acq]Xl+D∗[p(j)]Xl[p[j]]}
在捕获模式中,估计 ε ^ a c q \hat\varepsilon_{acq} ε^acq和 ε ^ f \hat\varepsilon_{f} ε^f,然后通过它们的总和补偿CFO。在跟踪模式中,只估计$ ε ^ f \hat\varepsilon_{f} ε^f,然后通过它补偿CFO。