机器学习笔记之最优化理论与方法------凸集的简单认识[上]
引言
本节将介绍关于凸集的基本信息,包括概念 、基本性质以及常见凸集。
凸优化问题与凸集合凸函数的关系
在最优化问题范畴中,凸优化问题是一类常见的、并且性质优秀 的优化问题。一些情况下可以通过凸优化问题 来解决非凸优化问题。
而凸集合与凸函数决定了该优化问题是凸优化问题 。具体表现在:
在最优化问题概述中我们介绍了可行域的概念。它可能并不仅仅被定义域空间描述,并且也可能伴随着约束条件的限制。在这里为了简化问题,仅观察定义域空间的描述。
- 目标函数 f ( x ) f(x) f(x)是一个凸函数;
- 而 x x x的可行域 S ⇒ x ∈ S \mathcal S \Rightarrow x \in \mathcal S S⇒x∈S是一个凸集合。
{ min f ( x ) s.t. x ∈ S \begin{cases} \min f(x) \\ \text{s.t. } x \in \mathcal S \end{cases} {minf(x)s.t. x∈S
凸优化问题简单示例
这里通过两个简单示例 描述凸优化相关的优秀性质:
- 关于一元函数 G ( x ) \mathcal G(x) G(x)的最小化问题数学符号 表示如下:
{ min G ( x ) s.t. x ∈ [ a , b ) \begin{cases} \min \mathcal G(x) \\ \text{s.t. } x \in [a,b) \end{cases} {minG(x)s.t. x∈[a,b) - 假设关于 G ( x ) \mathcal G(x) G(x)的函数图像 表示如下:

观察左侧 函数图像,在 [ a , b ) [a,b) [a,b)区间内,可以找到该函数的最小点,并且该点是一个平稳点------在该点处函数的导数 为 0 0 0;
同时观察右侧 函数图像,同样可以找到该函数的最小点。只不过区别于左侧 函数图像的是:该区间内函数的平稳点存在若干个:
- 观察第一、第三个红色点,它们都是其各自邻域内 的最小值,也称作局部最优解;其中第一个红色点不仅是局部最优解 ,而且是 [ a , b ) [a,b) [a,b)范围内的全局最优解。
但这些红色点也同样都是平稳点,也就是说:仅通过平稳点无法确定其是否为全局最优解。 - 再回顾左侧 函数图像:它的局部最优解就是全局最优解,并且平稳点对应的解就是全局最优解。
这是凸函数的重要性质;相反地,右侧图像描述的函数被称作非凸函数。
凸集的简单示例
已知函数: G ( x 1 , x 2 ) = x 1 2 + x 2 2 \mathcal G(x_1,x_2) = x_1^2 + x_2^2 G(x1,x2)=x12+x22,想要求解在可行域 S \mathcal S S内关于 G ( x 1 , x 2 ) \mathcal G(x_1,x_2) G(x1,x2)的最小值 。对应优化问题 表示如下:
{ min G ( x 1 , x 2 ) = x 1 2 + x 2 2 s.t. ( x 1 , x 2 ) ∈ S \begin{cases} \min \mathcal G(x_1,x_2) = x_1^2 + x_2^2 \\ \text{s.t. } (x_1,x_2) \in \mathcal S \end{cases} {minG(x1,x2)=x12+x22s.t. (x1,x2)∈S
现在存在两个可行域 S 1 , S 2 \mathcal S_1,\mathcal S_2 S1,S2,对应图像表示如下:

从几何角度观察,函数 G ( x 1 , x 2 ) \mathcal G(x_1,x_2) G(x1,x2)描述的图像形状 是圆,上述图像中的虚线 表示函数图像可能出现的等值线。
-
观察左侧 图像,在可行域 S 1 \mathcal S_1 S1范围内取到合适的 x ∗ ( x 1 ∗ , x 2 ∗ ) x^*(x_1^*,x_2^*) x∗(x1∗,x2∗),使得 G ( x 1 ∗ , x 2 ∗ ) \mathcal G(x_1^*,x_2^*) G(x1∗,x2∗)达到最小,很明显,是上述的红色点。作为最优解的 x ∗ x^* x∗,可以发现: x ∗ x^* x∗点所在位置是函数 G ( x 1 , x 2 ) \mathcal G(x_1,x_2) G(x1,x2)与可行域 S 1 \mathcal S_1 S1描述范围的切点;也就是说: x ∗ x^* x∗点处的负梯度方向 − ∇ G ( x 1 ∗ , x 2 ∗ ) -\nabla \mathcal G(x_1^*,x_2^*) −∇G(x1∗,x2∗)与切线方向垂直。
其中红色箭头表示负梯度方向。关于负梯度方向,详见线搜索方法(方向角度)。这意味着:从可行域 S 1 \mathcal S_1 S1范围内任取一点 x x x,那么向量 x − x ∗ x - x^* x−x∗与负梯度方向 之间的夹角总是 ≥ 9 0 o \geq 90^o ≥90o。如果用向量内积 的形式表示,必然有:
这里的G ( x ∗ ) \mathcal G(x^*) G(x∗)表示∇ G ( x 1 ∗ , x 2 ∗ ) \nabla \mathcal G(x_1^*,x_2^*) ∇G(x1∗,x2∗),后续同理。
− [ ∇ G ( x ∗ ) ] T ( x − x ∗ ) ≤ 0 ∀ x ∈ S 1 -[\nabla \mathcal G(x^*)]^T(x - x^*) \leq 0 \quad \forall x \in \mathcal S_1 −[∇G(x∗)]T(x−x∗)≤0∀x∈S1最终归纳得到如下等价条件:
x ∗ is Optimal ⇔ − [ ∇ G ( x ∗ ) ] T ( x − x ∗ ) ≤ 0 ∀ x ∈ S 1 x^* \text{ is Optimal } \Leftrightarrow -[\nabla \mathcal G(x^*)]^T(x - x^*) \leq 0 \quad \forall x \in \mathcal S_1 x∗ is Optimal ⇔−[∇G(x∗)]T(x−x∗)≤0∀x∈S1 -
观察右侧 图像,可以按照上述寻找切点的方式去寻找最优解 。假设找到了右侧的红色点。但这个最优解并不满足上述的等价条件。
见下图中右侧两个红色箭头明显是一个锐角。

综上,可行域内任意一点 x x x与最优解 x ∗ x^* x∗之间满足如上等价条件,那么该可行域是凸集 ;反之为非凸集。从而将可行域 S 1 \mathcal S_1 S1称为凸集;而可行域 S 2 \mathcal S_2 S2称作非凸集。相反,如果一个可行域 被确定是凸集,那么它同样存在一些优秀性质:
- 在凸集 中根据上述等价条件找到的最优解一定是全局最优解;
- 通过求解导数/梯度 获取的平稳定一定是最值点。
基本定义:凸集
关于凸集 ( Convex Set ) (\text{Convex Set}) (Convex Set)的定义表示如下:
∀ x , y ∈ C ; ∀ λ ∈ [ 0 , 1 ] ⇒ λ ⋅ x + ( 1 − λ ) ⋅ y ∈ C \forall x,y \in \mathcal C;\forall \lambda \in [0,1] \Rightarrow \lambda \cdot x + (1 - \lambda) \cdot y \in \mathcal C ∀x,y∈C;∀λ∈[0,1]⇒λ⋅x+(1−λ)⋅y∈C
文字的描述可简单表述为:可行域 C \mathcal C C中任意两点间的连线,其连线上的任一点仍属于该可行域 C \mathcal C C。示例图像表示如下:
第二张图也被称作多面体。很明显,最后一个图描述的可行域不是凸集,其连线上的点并不全在可行域上。

关于凸集性质的等价条件,凸组合,凸包
关于凸集合性质 存在如下等价条件:如果某可行域 C \mathcal C C是一个凸集,对于 ∀ x 1 , x 2 , ⋯ , x k ∈ C \forall x_1,x_2,\cdots,x_k \in \mathcal C ∀x1,x2,⋯,xk∈C,且对于 ∀ λ 1 , λ 2 , ⋯ , λ k ≥ 0 \forall \lambda_1,\lambda_2,\cdots,\lambda_k \geq0 ∀λ1,λ2,⋯,λk≥0且 ∑ i = 1 k λ i = 1 \begin{aligned}\sum_{i=1}^{k} \lambda_i = 1\end{aligned} i=1∑kλi=1,必然有:
反之同样可以推出 C \mathcal C C是一个凸集。
∑ i = 1 k λ i ⋅ x i ∈ C \sum_{i=1}^k \lambda_i \cdot x_i \in \mathcal C i=1∑kλi⋅xi∈C
这里以 k = 3 k=3 k=3为例。对于 x 1 , x 2 , x 3 ∈ C , ∀ λ 1 , λ 2 , λ 3 ≥ 0 x_1,x_2,x_3 \in \mathcal C, \forall \lambda_1,\lambda_2,\lambda_3 \geq 0 x1,x2,x3∈C,∀λ1,λ2,λ3≥0且 λ 1 + λ 2 + λ 3 = 1 \lambda_1+\lambda_2 + \lambda_3 = 1 λ1+λ2+λ3=1,对应 λ 1 x 1 + λ 2 x 2 + λ 3 x 3 \lambda_1x_1 + \lambda_2x_2 + \lambda_3x_3 λ1x1+λ2x2+λ3x3在可行域 C \mathcal C C中的描述 表示为: x 1 , x 2 , x 3 x_1,x_2,x_3 x1,x2,x3围成的三角形的范围:
显然,该三角形围成的范围是可行域 C \mathcal C C的一部分。

对于表达式 ∑ i = 1 k λ i ⋅ x i \begin{aligned}\sum_{i=1}^k \lambda_i \cdot x_i\end{aligned} i=1∑kλi⋅xi,它称作 x 1 , x 2 , ⋯ , x k x_1,x_2,\cdots,x_k x1,x2,⋯,xk的凸组合 ( Convex Combination ) (\text{Convex Combination}) (Convex Combination)。
条件不能漏掉~ λ i ( i = 1 , 2 , ⋯ , k ) ≥ 0 \lambda_i(i=1,2,\cdots,k) \geq 0 λi(i=1,2,⋯,k)≥0且 ∑ i = 1 k λ i = 1 \sum_{i=1}^k \lambda_i = 1 ∑i=1kλi=1。
相应的组合 概念如:
很明显,从关于 λ i ( i = 1 , 2 , ⋯ , k ) \lambda_i(i=1,2,\cdots,k) λi(i=1,2,⋯,k)的约束程度角度,有:凸组合 > > > 仿射组合;非负组合 > > > 线性组合。
- 线性组合 ( Linear Combination ) (\text{Linear Combination}) (Linear Combination): ∑ i = 1 k λ i ⋅ x i \sum_{i=1}^k \lambda_i \cdot x_i ∑i=1kλi⋅xi,虽然与凸组合共用相同的表达式,但其对 λ i ( i = 1 , 2 , ⋯ , k ) ∈ R \lambda_i(i=1,2,\cdots,k) \in \mathbb R λi(i=1,2,⋯,k)∈R即可,没有过多的约束;
- 仿射组合 ( Affine Combination ) (\text{Affine Combination}) (Affine Combination):依然是上述表达式,但相比于凸组合,只要求 ∑ i = 1 k λ i = 1 \sum_{i=1}^k \lambda_i = 1 ∑i=1kλi=1,没有符号要求。
- 非负组合 ( Nonnegative Combination ) (\text{Nonnegative Combination}) (Nonnegative Combination):依然是上述表达式,但相比于凸组合,仅要求 λ i ( i = 1 , 2 , ⋯ , k ) ≥ 0 \lambda_i(i=1,2,\cdots,k) \geq 0 λi(i=1,2,⋯,k)≥0,没有加和为 1 1 1的要求。
关于凸包 ( Convex Hull ) (\text{Convex Hull}) (Convex Hull),它针对的是任意一个集合 ,并非只有凸集。在选定集合 C \mathcal C C的条件下,从 C \mathcal C C中取点后作凸组合 ,将所有凸组合结果构成一个新集合,该集合被称作凸包。
凸包的作用:由于凸包是由凸组合 构成的集合,因而:对于任意集合 C \mathcal C C(凸、非凸),它的凸包一定是凸集合。从而凸包是优化过程中将非凸集合凸化的一个工具。
这里作为科普,不做过多描述~
常见凸集
常见的凸集合有:
- 超平面 ( Hyperplane ) (\text{Hyperplane}) (Hyperplane),其表达式表示如下:
H = { x ∣ a T x = b } ( a ≠ 0 ) \mathcal H = \{x \mid a^T x = b\}(a \neq 0) H={x∣aTx=b}(a=0) - 半空间 ( Halfspace ) (\text{Halfspace}) (Halfspace),其表达式表示为:
{ H + = { x ∣ a T x ≥ b } ( a ≠ 0 ) H − = { x ∣ a T x ≤ b } ( a ≠ 0 ) \begin{cases} \mathcal H^{+} = \{x \mid a^Tx \geq b \}(a \neq 0) \\ \mathcal H^{-} = \{x \mid a^Tx \leq b\}(a \neq 0) \end{cases} {H+={x∣aTx≥b}(a=0)H−={x∣aTx≤b}(a=0)
对应图像描述表示为:

- 多面体 ( Polyhedra ) (\text{Polyhedra}) (Polyhedra):由多个线性不等式 刻画的集合。对应表达式表示如下:
由于一个线性不等式刻画的是半空间,那么由多个线性不等式对应半空间的交集/围成的空间就是多面体。
{ x ∣ a i T x ≤ b i , i = 1 , 2 , ⋯ , M } \{x \mid a_i^T x \leq b_i,i=1,2,\cdots,\mathcal M\} {x∣aiTx≤bi,i=1,2,⋯,M}
关于多面体集合 P \mathcal P P的图像示例描述表示为:

上面关于多面体 的定义是关于线性不等式所刻画的集合;相反,线性等式刻画的集合是多面体吗 ? ? ?自然也是。因为可以将线性等式 a i T x = b i a_i^T x = b_i aiTx=bi刻画为如下两个线性不等式 的交集:
从而又将线性等式刻画的集合转化为线性不等式刻画的集合。
a i T x = b i ⇔ { a i T x ≤ b i − a i T x ≤ − b i i = 1 , 2 , ⋯ , M a_i^T x = b_i \Leftrightarrow \begin{cases} a_i^T x \leq b_i \\ -a_i^T x \leq -b_i \end{cases} \quad i=1,2,\cdots,\mathcal M aiTx=bi⇔{aiTx≤bi−aiTx≤−bii=1,2,⋯,M - 欧几里得球 ( Euclidean Balls ) (\text{Euclidean Balls}) (Euclidean Balls):如果球的中心 x c x_{c} xc和半径 r r r已知,对应表达式表示如下:
这里的∣ ∣ u ∣ ∣ 2 ≤ 1 ||u||2 \leq 1 ∣∣u∣∣2≤1描述的是中心为0 0 0,半径为1 1 1的单位球空间。对应的r ⋅ u r \cdot u r⋅u则表示对球空间进行放缩;x c + r ⋅ u x_c + r \cdot u xc+r⋅u则是对放缩后的结果进行平移~
B ( x c , r ) = { x ∣ ∥ x − x c ∥ 2 ≤ r } = { x c + r ⋅ u ∣ ∥ u ∥ 2 ≤ 1 } \begin{aligned} \mathcal B(x{c},r) & = \{x \mid \| x - x_c\|_2 \leq r\} \\ & = \{x_c + r \cdot u \mid \|u\|_2 \leq 1\} \end{aligned} B(xc,r)={x∣∥x−xc∥2≤r}={xc+r⋅u∣∥u∥2≤1}
这仅仅是二范数 的结果,调整范数 ,可以得到范数球 ( Norm Balls ) (\text{Norm Balls}) (Norm Balls)。
相关文章见下方链接~ - 椭球 ( Ellipsoid ) (\text{Ellipsoid}) (Ellipsoid):若椭球中心 x c x_c xc已知,对应表达式表示如下:
其中矩阵P \mathcal P P是正定矩阵,否则P − 1 \mathcal P^{-1} P−1无法求解。
{ x ∣ ( x − x c ) T P − 1 ( x − x c ) ≤ 1 } \{x \mid (x -x_c)^T \mathcal P^{-1} (x - x_c) \leq 1\} {x∣(x−xc)TP−1(x−xc)≤1}
为什么是 P − 1 \mathcal P^{-1} P−1,它有什么作用 ? ? ?这里假设正定矩阵 P \mathcal P P与对应 P − 1 \mathcal P^{-1} P−1表示如下:
P = ( 2 0 0 4 ) ⇒ P − 1 = ( 1 2 0 0 1 4 ) \mathcal P = \begin{pmatrix}2 \quad 0 \\ 0 \quad 4\end{pmatrix} \Rightarrow \mathcal P^{-1} = \begin{pmatrix} \begin{aligned}\frac{1}{2} \quad 0 \\ 0 \quad \frac{1}{4}\end{aligned} \end{pmatrix} P=(2004)⇒P−1= 210041
将 P − 1 \mathcal P^{-1} P−1带入到原式,有:
( x − x c ) T ( 1 / 2 0 0 1 / 4 ) ( x − x c ) ≤ 1 (x - x_c)^T \begin{pmatrix}1/2 \quad 0 \\ 0 \quad 1/4\end{pmatrix}(x - x_c) \leq 1 (x−xc)T(1/2001/4)(x−xc)≤1
从而有:
( x 1 − x c 1 ) 2 2 + ( x 2 − x c 2 ) 2 4 ≤ 1 \frac{(x_1 - x_{c_1})^2}{2} + \frac{(x_2 - x_{c_2})^2}{4} \leq 1 2(x1−xc1)2+4(x2−xc2)2≤1
上式中描述的椭球空间,其长轴、短轴的半轴长 分别是 2 , 4 \sqrt{2},\sqrt{4} 2 ,4 ,这恰好是正定矩阵 P \mathcal P P特征值的开平方。因此 P − 1 \mathcal P^{-1} P−1本质上描述 P \mathcal P P与椭球长短轴之间的关联关系。 - 二阶锥 ( Second-Order Cone ) (\text{Second-Order Cone}) (Second-Order Cone)
关于锥集合 C \mathcal C C的定义可描述为:
if x ∈ C ⇒ λ ⋅ x ∈ C ∀ λ ≥ 0 \text{if } x \in \mathcal C \Rightarrow \lambda \cdot x \in \mathcal C \quad \forall \lambda \geq 0 if x∈C⇒λ⋅x∈C∀λ≥0
而二阶锥的定义可表示为:
假设在n + 1 n+1 n+1维的特征空间中,其中x = ( x 1 , x 2 , ⋯ , x n ) T ∈ R n x = (x_1,x_2,\cdots,x_n)^T \in \mathbb R^n x=(x1,x2,⋯,xn)T∈Rn,最后一维特征表示为t t t。下面公式则表示为:前 n n n维的二范数结果 ∣ ∣ x ∣ ∣ 2 ≤ ||x||_2 \leq ∣∣x∣∣2≤第 n + 1 n+1 n+1维的特征结果 t t t。
{ ( x , t ) ∣ ∥ x ∥ 2 ≤ t } \{(x,t) \mid \|x\|_2 \leq t\} {(x,t)∣∥x∥2≤t}
例如: x x x是一个二维向量,那么上式的表达有:
x 1 2 + x 2 2 ≤ t \sqrt{x_1^2 + x_2^2} \leq t x12+x22 ≤t
简单绘制一下它的图像:
python
import numpy as np
import matplotlib.pyplot as plt
import math
x = np.linspace(-5,5,50)
y = np.linspace(-5,5,50)
t = 5.0
def f(x,y):
return math.sqrt((x ** 2) + (y ** 2))
ax = plt.axes(projection='3d')
for i in list(x):
for j in list(y):
if f(i,j) <= t:
ax.scatter(i,j,f(i,j),c="tab:blue",s=2)
else:
continue
plt.show()最终结果表示如下:

-
半定矩阵锥:
- 首先,划定一个集合 S n \mathcal S^n Sn,它描述:所有 n n n阶对称矩阵组成的集合;
可见,集合中的每个元素都是n n n阶对称矩阵。 - 在集合 S n \mathcal S^n Sn的基础上,划定一个集合 S + n \mathcal S_{+}^n S+n,它描述:所有 n n n阶半正定矩阵组成的集合,记作 S + n = { X ∈ S n ∣ X ≽ 0 } \mathcal S_{+}^n = \{\mathcal X \in \mathcal S^n \mid \mathcal X \succcurlyeq 0\} S+n={X∈Sn∣X≽0}
其中X ≽ 0 ⇔ Z T X Z ≥ 0 ∀ Z \mathcal X \succcurlyeq 0 \Leftrightarrow \mathcal Z^T \mathcal X \mathcal Z \geq 0 \quad \forall \mathcal Z X≽0⇔ZTXZ≥0∀Z。 - 同样在集合 S n \mathcal S^n Sn的基础上,划定一个集合 S + + n \mathcal S_{++}^n S++n,它描述:所有 n n n阶正定矩阵组成的集合,记作 S + + n = { X ∈ S n ∣ X ≻ 0 } \mathcal S_{++}^n = \{\mathcal X \in \mathcal S^n \mid \mathcal X \succ 0\} S++n={X∈Sn∣X≻0}
同上:X ≻ 0 ⇔ Z T X Z > 0 ∀ Z \mathcal X \succ 0 \Leftrightarrow \mathcal Z^T \mathcal X \mathcal Z > 0 \quad \forall \mathcal Z X≻0⇔ZTXZ>0∀Z
对于集合 S + n \mathcal S_{+}^n S+n中的元素 X \mathcal X X,它们必然是半正定矩阵 。因而 λ ⋅ X ( ∀ λ ≥ 0 ) \lambda \cdot \mathcal X (\forall \lambda \geq 0) λ⋅X(∀λ≥0)依然是半正定矩阵 。因而满足锥集合的定义:
X ∈ S + n ⇒ λ ⋅ X ∈ S + n λ ≥ 0 \mathcal X \in \mathcal S_{+}^n \Rightarrow \lambda \cdot \mathcal X \in \mathcal S_{+}^n \quad \lambda \geq 0 X∈S+n⇒λ⋅X∈S+nλ≥0因而集合 S + n \mathcal S_{+}^n S+n是锥集合。
新的问题:锥集合 S + n \mathcal S_{+}^n S+n是不是凸集合 ? ? ?根据凸集合的定义,有:
- 从集合 S + n \mathcal S_{+}^n S+n中任意选择一系列半正定矩阵 :
∀ x 1 , x 2 , ⋯ , x k ∈ S + n \forall x_1,x_2,\cdots,x_k \in \mathcal S_{+}^n ∀x1,x2,⋯,xk∈S+n - 选择 λ i ( i = 1 , 2 , ⋯ , k ) \lambda_i(i=1,2,\cdots,k) λi(i=1,2,⋯,k)满足:
{ λ i ≥ 0 i = 1 , 2 , ⋯ , k ∑ i = 1 k λ i = 1 \begin{cases} \lambda_i \geq 0 \quad i=1,2,\cdots,k \\ \sum_{i=1}^k \lambda_i = 1 \end{cases} {λi≥0i=1,2,⋯,k∑i=1kλi=1 - 观察: ∑ i = 1 k λ i ⋅ x i \sum_{i=1}^k \lambda_i \cdot x_i ∑i=1kλi⋅xi中每一项 λ i ⋅ x i ( i = 1 , 2 , ⋯ , k ) \lambda_i \cdot x_i(i=1,2,\cdots,k) λi⋅xi(i=1,2,⋯,k)均是半正定矩阵,因而 ∑ i = 1 k λ i ⋅ x i \sum_{i=1}^k \lambda_i \cdot x_i ∑i=1kλi⋅xi必然也是半正定矩阵。即:
∑ i = 1 k λ i ⋅ x i ∈ S + n \sum_{i=1}^k \lambda_i \cdot x_i \in \mathcal S_{+}^n i=1∑kλi⋅xi∈S+n
因此锥集合 S + n \mathcal S_{+}^n S+n必然是凸集合。
关于半定矩阵锥的图像,以二阶矩阵为例。如果二阶矩阵 ( x y y z ) ∈ S + 2 \begin{pmatrix}x \quad y \\ y \quad z\end{pmatrix} \in \mathcal S_{+}^2 (xyyz)∈S+2,也就是说:该二阶矩阵是一个半正定矩阵。如何判定一个矩阵是半正定 的 ? ? ?
- 主对角线元素 x , z ≥ 0 x,z \geq 0 x,z≥0;
- 该矩阵的顺序主子式 : x ⋅ z − y 2 ≥ 0 x \cdot z - y^2\geq 0 x⋅z−y2≥0;
- 同样绘制它的图像:
这里的图像不容易看,像个船头~大家自己多试试角度~
- 首先,划定一个集合 S n \mathcal S^n Sn,它描述:所有 n n n阶对称矩阵组成的集合;
python
import numpy as np
import matplotlib.pyplot as plt
import tqdm
x = np.linspace(-5,5,20)
y = np.linspace(-5,5,20)
z = np.linspace(-5,5,20)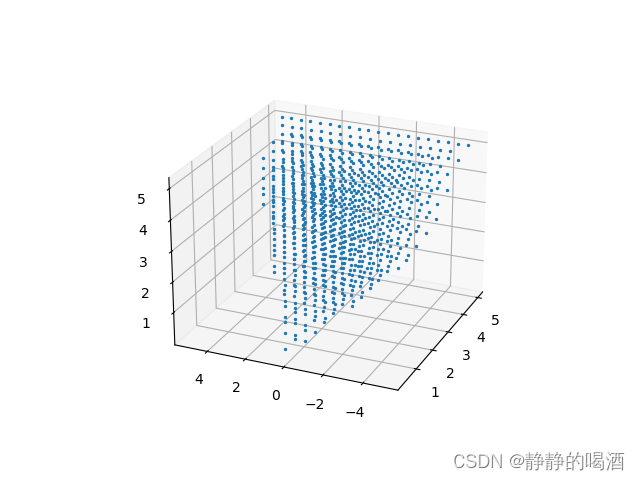
def SequentialPrincipalMinor(x,y,z):
return x * z - (y ** 2)
ax = plt.axes(projection='3d')
for i in tqdm(list(x)):
for j in list(y):
for k in list(z):
if i >= 0 and k >= 0 and SequentialPrincipalMinor(i,j,k) >= 0:
ax.scatter(i,j,k,c="tab:blue",s=2)
else:
continue
plt.show()最终结果表示如下:

个人理解 :集合 S + + n \mathcal S_{++}^n S++n不仅是锥集合,并且也是凸集合。
这个图就不贴了,和上面的结果很像~
- 关于 ∑ i = 1 k λ i ⋅ x i x i ∈ S + + n \begin{aligned}\sum_{i=1}^k \lambda_i \cdot x_i \quad x_i \in \mathcal S_{++}^n\end{aligned} i=1∑kλi⋅xixi∈S++n,只要 λ i ⋅ x i ( i = 1 , 2 , ⋯ , k ) \lambda_i \cdot x_i(i=1,2,\cdots,k) λi⋅xi(i=1,2,⋯,k)中至少有一项是正定矩阵 ,那么 ∑ i = 1 k λ i ⋅ x i \begin{aligned}\sum_{i=1}^k \lambda_i \cdot x_i \end{aligned} i=1∑kλi⋅xi必然是正定矩阵。
- 由于 ∑ i = 1 k λ i = 1 \begin{aligned}\sum_{i=1}^k \lambda_i =1\end{aligned} i=1∑kλi=1,因而不可能出现 λ 1 = λ 2 = ⋯ = λ k = 0 \lambda_1 = \lambda_2 = \cdots = \lambda_k = 0 λ1=λ2=⋯=λk=0。也就是说:必然存在项 λ i > 0 \lambda_i > 0 λi>0,从而使 λ i ⋅ x i \lambda_i \cdot x_i λi⋅xi是正定矩阵。
Process : 43 : 34 / 1 : 21 : 31 \text{Process}: 43:34/1:21:31 Process:43:34/1:21:31