一、定义:
快速排序是Hoare于1962年提出的一种二叉树结构的交换排序方法(也叫Hoare排序),是一种基于分治 的排序方。其基本原理是将待排序的数组 通过一趟排序 分成两个独立的部分 ,其中一部分的所有数据比另一部分的所有数据都要小 ,然后再按此方法对这两部分数据分别进行快速排序,整个排序过程可以递归进行,以此达到整个数据变成有序序列(非递归也是可行的,需要借助数据结构栈来实现)
二、递归思想:
排序只讲升序,升序和降序也就是大于和小于逻辑上的差别
Hoare法:
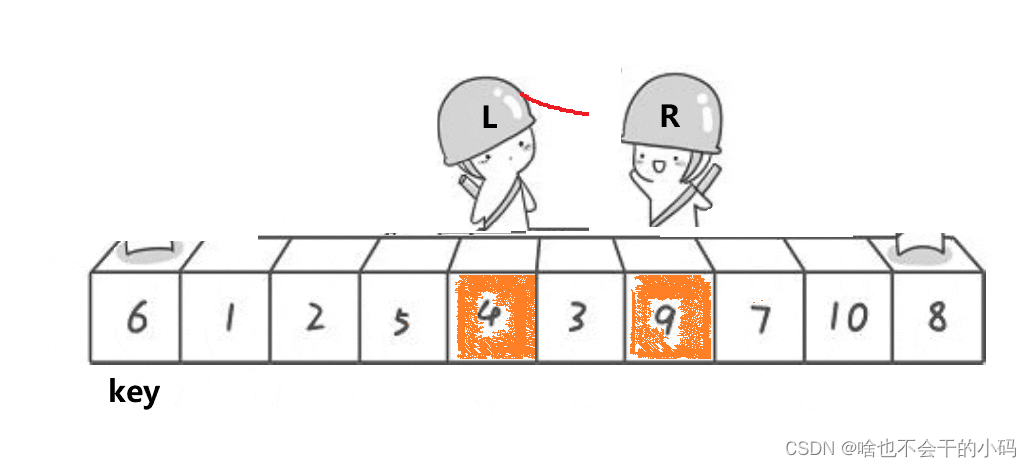
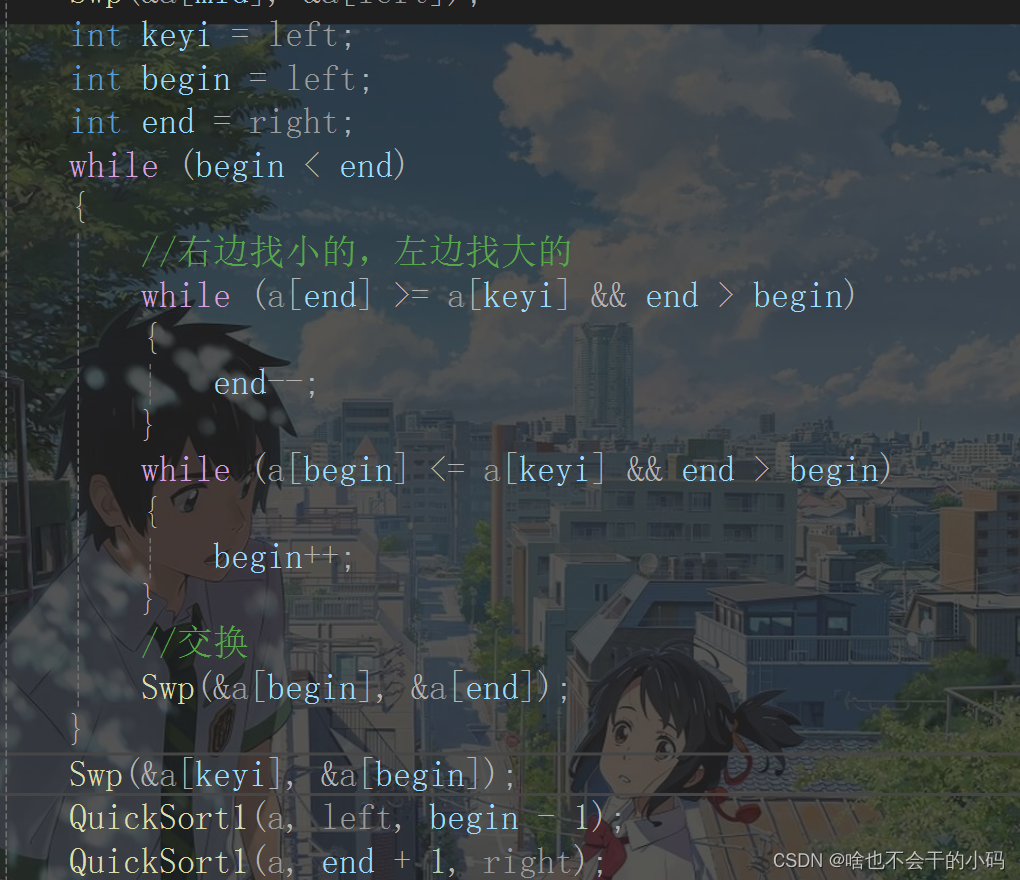
1、设置一个keyi记录头位置的数据,然后设计2个指分别为针end和begin; 一个从右边出发,一个从左边出发
2、end所指向的数据若是小于keyi则停下,然后begin走,所指向的数据若是大于keyi则停下,
3、将end和begin指向的元素进行互换
4、继续让end走,然后begin走,重复2-3,直到2者相遇,若是相遇,则将其与keyi指向的元素进交换,完成一次✨👉👉
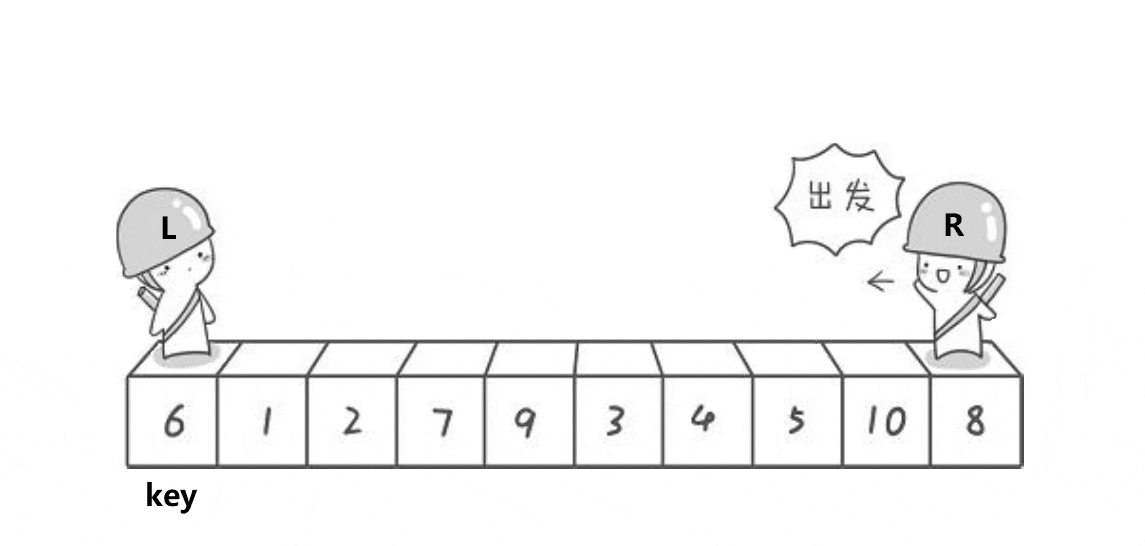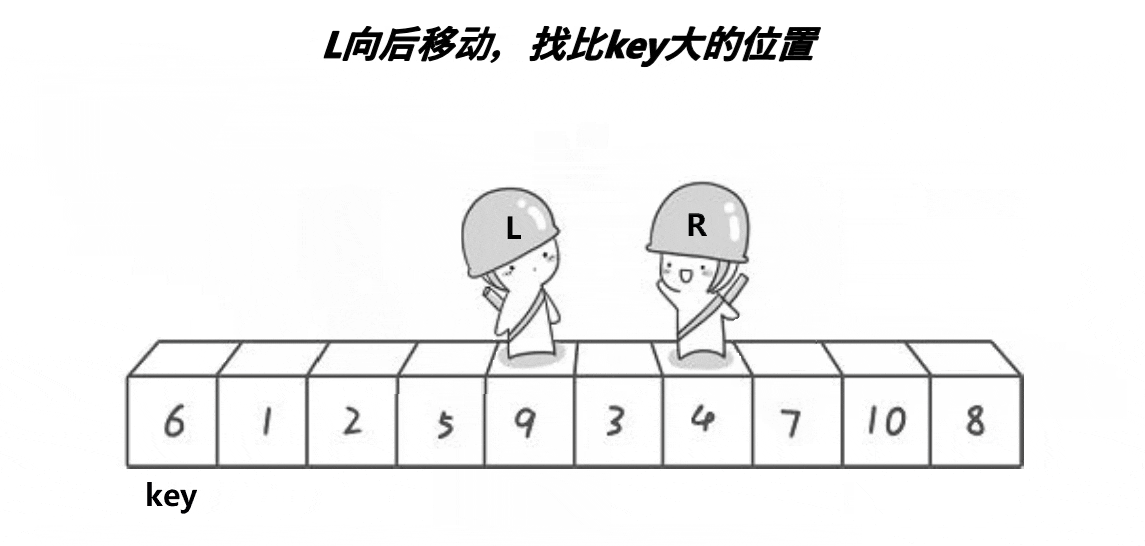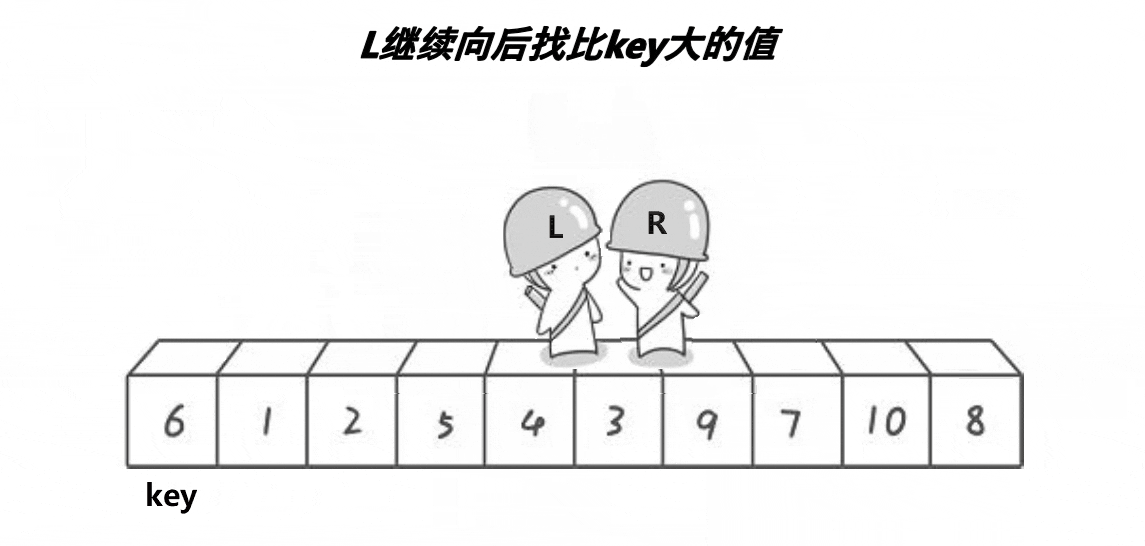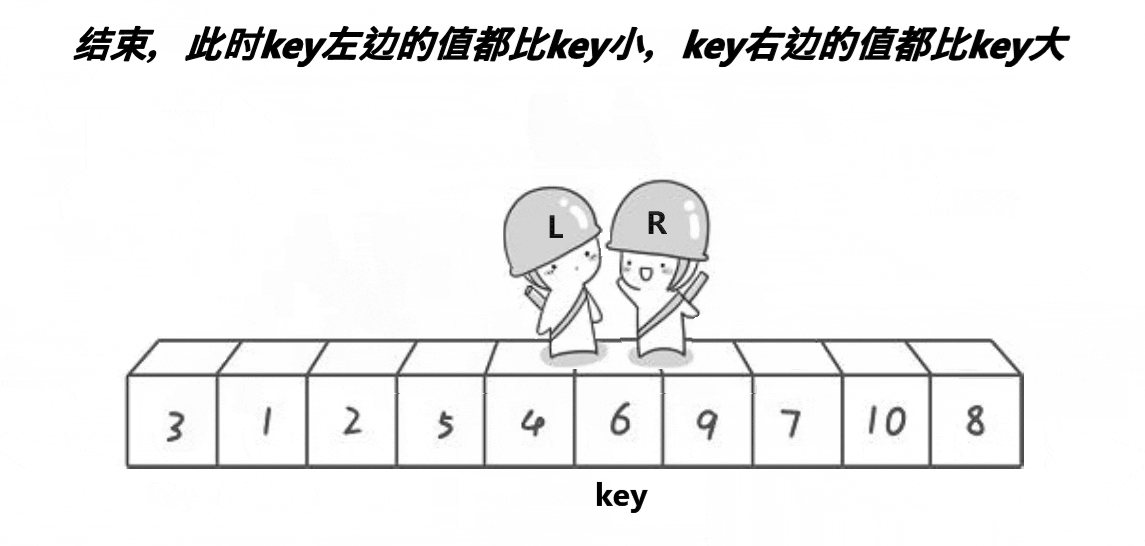
5、keyi指向的数据的位置不是交换到了end和begin相遇的地方么,我们从这里以此处为界限,将区间分成2部分👉👉👉
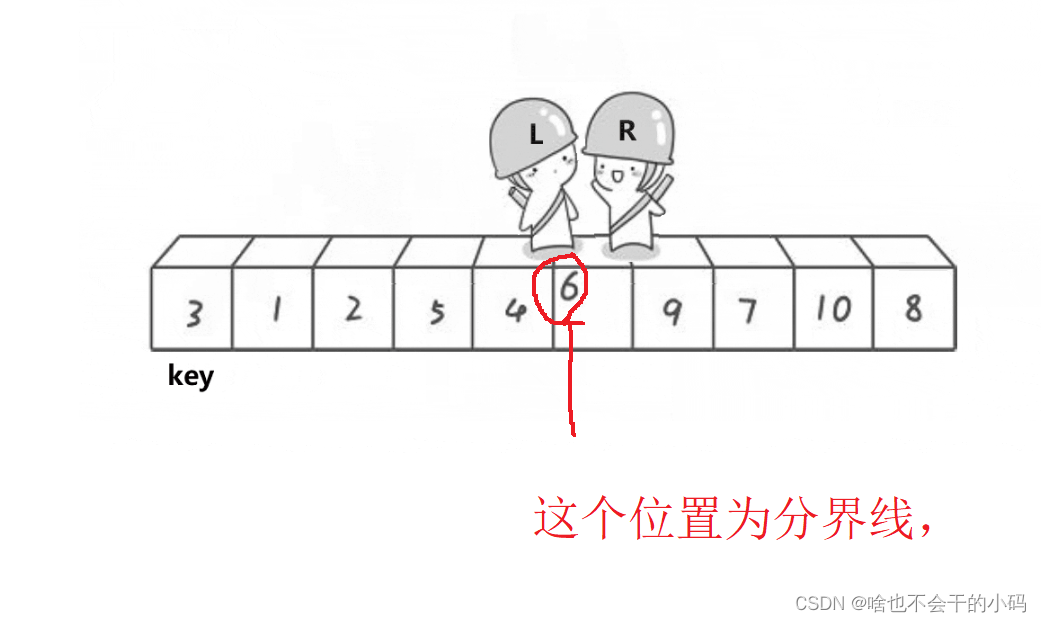
也就是说我们要对左和右区间分别进行上述操作(2个人走路对比交换操作),完成2个区间,2个区间又会分化成4个区间,一直进行下去,分到区间只有一个数据就实现了。🤔🤔🤔有点类似与二叉树里的前序遍历的思想✨✨✨
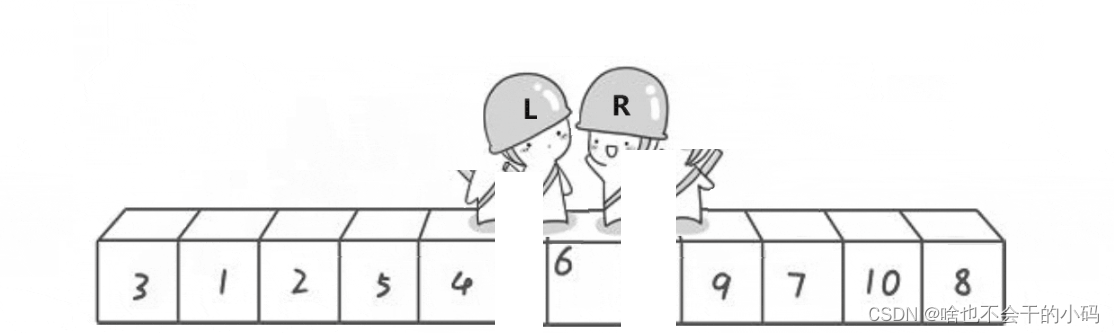
我们发现走完一次中间值的特点是左边全部小于他,右边全部大于他
我们走路的先后是有讲究的,2个人不是同时走的,而是一个人先走,一个人慢走,也就是说满足这个特点的话讲究先后顺序,因为决定了谁先遇见谁 那么如果我要左边先走了????🤔
✨✨✨用图来说话,是不是不能满足了;
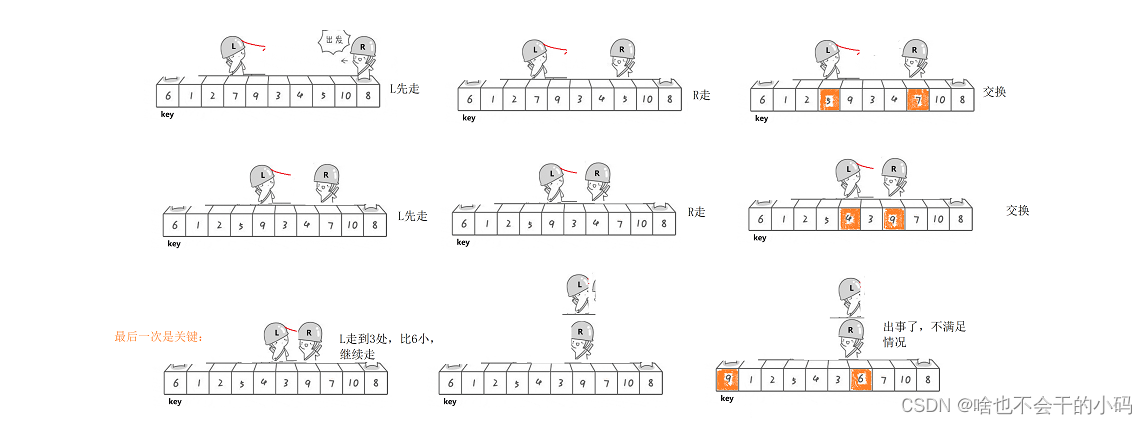
🐸🐸hoare排序的难点在这里,就是要注意谁先走;为啥会有这种情况??
✨✨因为我们左边的任务是找大 ,右边的任务是找小 ,然后而且我们的2个好兄弟并不是同时走的,是交替顺序走的哦!🧑🎓🧑🎓相遇前的最后一次 发生的交换,如下:这是互换好的
此时🐸左边大于keyi的数换到了end的位置,🐸右边小于keyi的数换到了begin的位置。🤔如果先走begin ;begin走到end的位置停下,也就是我们会将大于keyi的数和其交换位置,所以不满足情况;若是先走end, 那么end和begin相遇就是停在小于keyi的位置✨✨
其实这个才是影响最终结果的情况
👉✨总结:"先出发是为了在你遇见我之前而遇见你"---->>> 我如果keyi 的位置在首元素位置,和keyi进行互换的元素需要是小于keyi指向的元素,那么就需要任务为:找大于keyi的数的end指针先走; 如果keyi 在尾元素处 ,最后与keyi交换的元素要大于keyi指向的元素,那么我们需要的是任务为:找大于keyi的begin指针先走。✨✨✨✨✨✨✨✨✨✨✨✨✨
Hoare的思路差不多讲完了,是不是感觉已经可以自己写出代码了✨✨✨✨确实如此哈,但是你这会递归吗??🧐 哈哈哈,开玩笑啦❤️🫰笔者当然相信你会的,试着自己写一下嘛😁作为笔记,我还是记录一下
🧑🎓✨开始时就说过Hoare排序类似二叉树的前序 ,先排序,当keyi换好位置后,将其当作**"根节点"** 并分成2个区间,2个区间又进行排序,将keyi位置交换好,再次以keyi根分成2个区间,重复排序,一直分到区间只有一个元素,也就有序了,👉👉👉这个图就是先分区间,排序好后,分成2部分,因为每次排一次keyi交换后, 他的左边全是小于 他的值右边全是大于他的值,每个区间的都有这样的特性,因此传参传的是区间✨
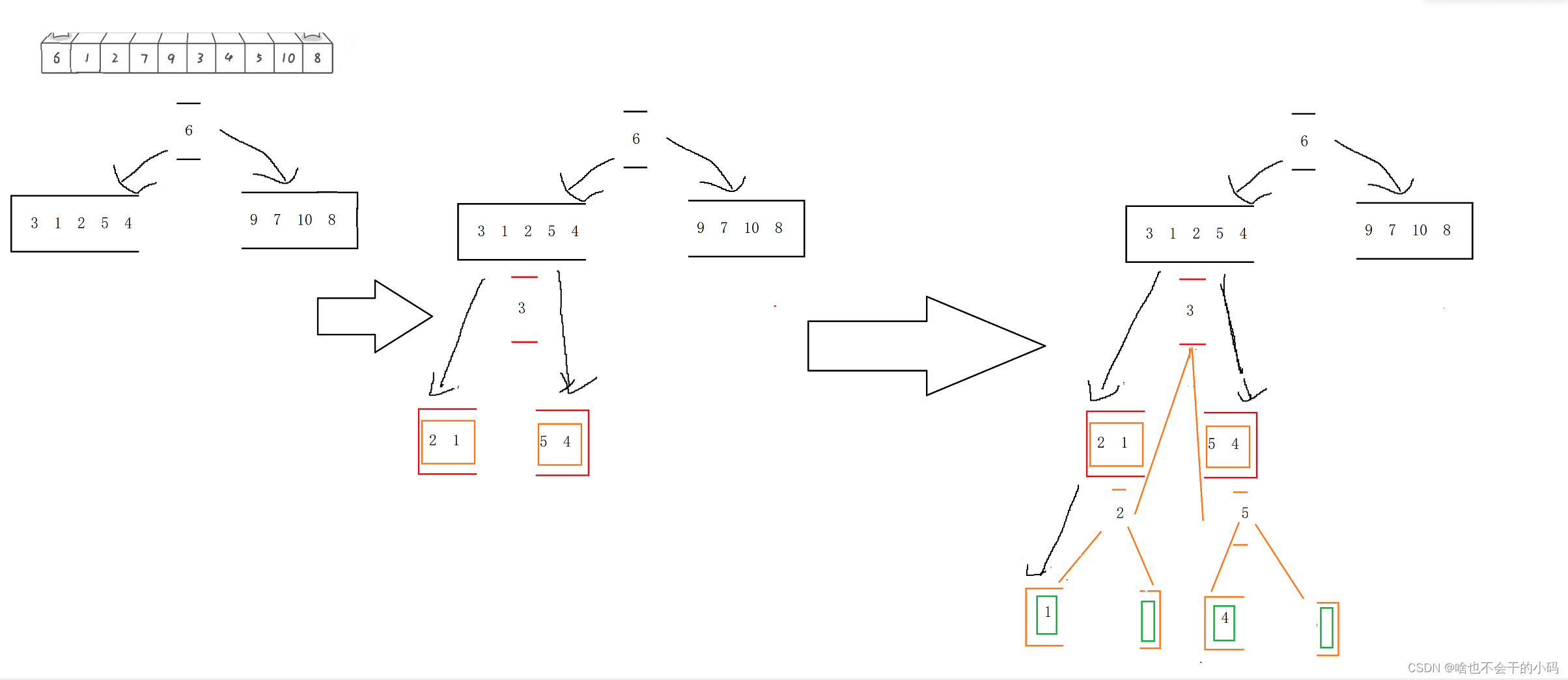
我们排号区间,以节点作为区间分界点进行分割区间,如6的左右2边分成了2块区间
优化1:keyi的选取
✨✨其实上面的递归看着是个二叉树的样子,keyi每次都换在区间中间的情况,并不是每次都是这样,根据待排序数组来看的哦🐸 数据顺序千变万化;
👉比如:一个逆序的数组,你将数据传入,那么keyi直接交换到最后一个位置,以最后一个位置分成一个区间;看图,发现了么,我还有重复排序情况,很容易发生栈溢出的风险☠️☠️
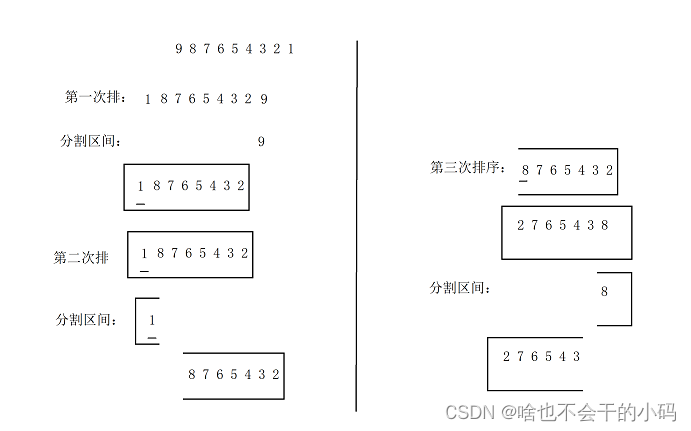
如果是 顺序的也是如此👉👉👉👉
时间复杂度退化到O(N^2)🤔🤔
因为keyi每次都是取首元素的值,所以会出现上述这种弊端,从keyi取值入手
1、随机值 (keyi的值是随机的,但是不推荐,随机值不好控制)
2、三数取中(在区间里面,左、右、中三个数取第二大的数到keyi里去)
**注意:**并不是keyi要换到这些位置,而是将取到值换到keyi指向的位置,因为我们本身的逻辑keyi就必须是在首元素位置✨✨
👉三数取中就可以避免上面的情况,数据左、右值以及中间值,三个数里面找中间值 ,然后将中间值换到首元素位置(逻辑不能变,keyi的位置初始情况在首元素✨);就可以保证排好序后,keyi的位置接近区间的中间
cpp
//优化:先三个数找中间:
int GetMin(int* a, int left, int right)
{
int min = ((right - left) >> 1)+ left;
if (a[min] < a[left])
{
if (a[min] > a[right])
{
return min;
}
else if (a[right]<a[left])
{
return right;
}
else
{
return left;
}
}
else
{
if (a[min] < a[right])
{
return min;
}
else if (a[right] > a[left])
{
return right;
}
else
{
return left;
}
}
}优化2:小区间优化
每次分割二分,以二叉树角度看,最后一层是2^(h-1)个节点,总节点是2^h,那么我发现倒数三层占递归比例挺大的哎,我能不能把这一段优化掉???不用递归了,降低栈溢出的风险🤔🤔
这里我们想到用一个**时间复杂度为O(N^2)**的排序来解决
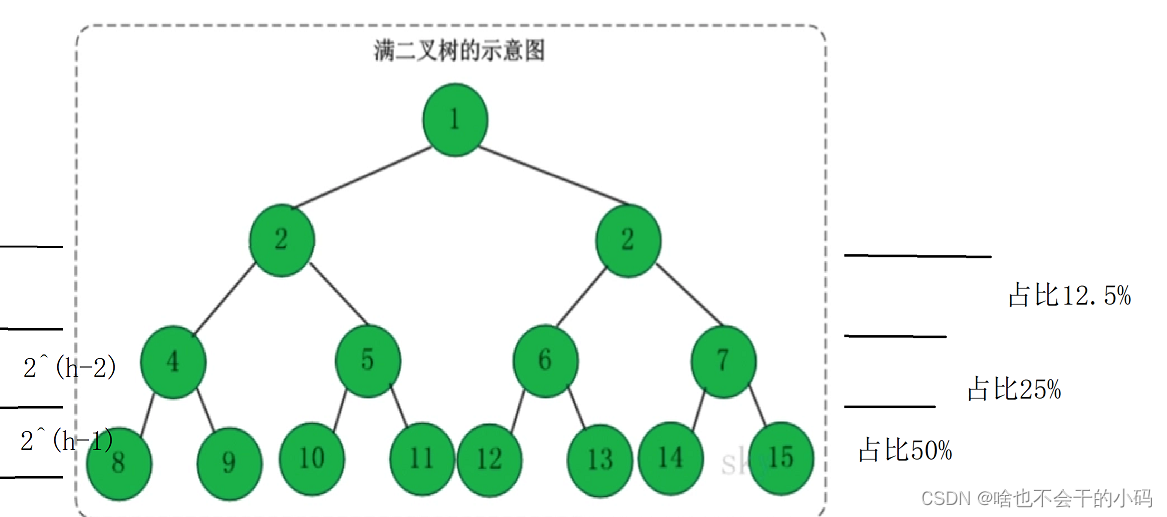
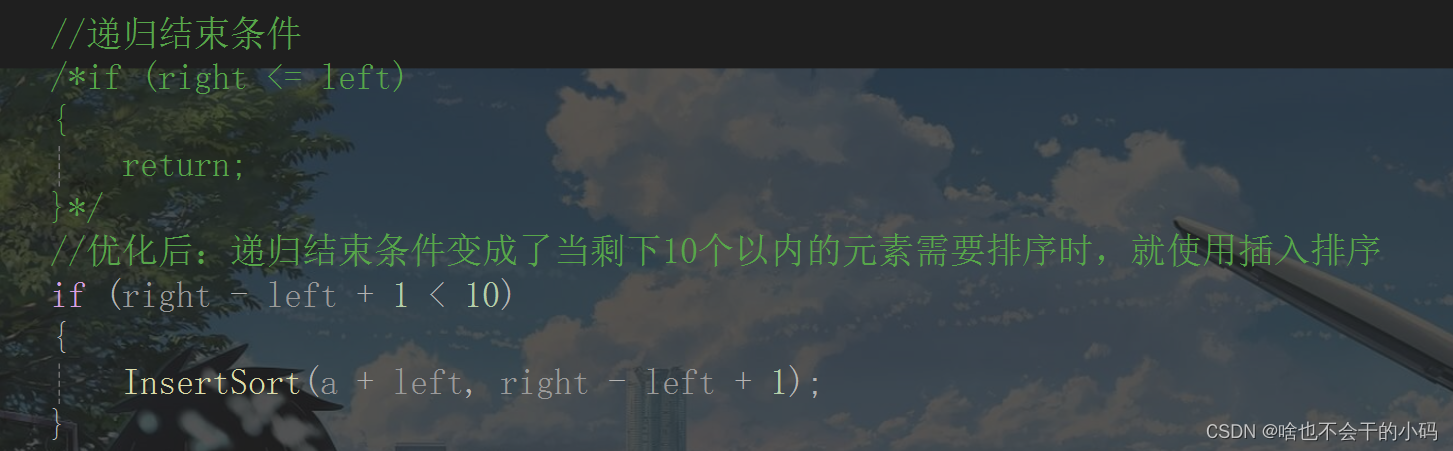
当区间元素个数小于10个时我就用一个**插入排序 。**修改一下递归条件即可递归结束条件即可
挖坑法: 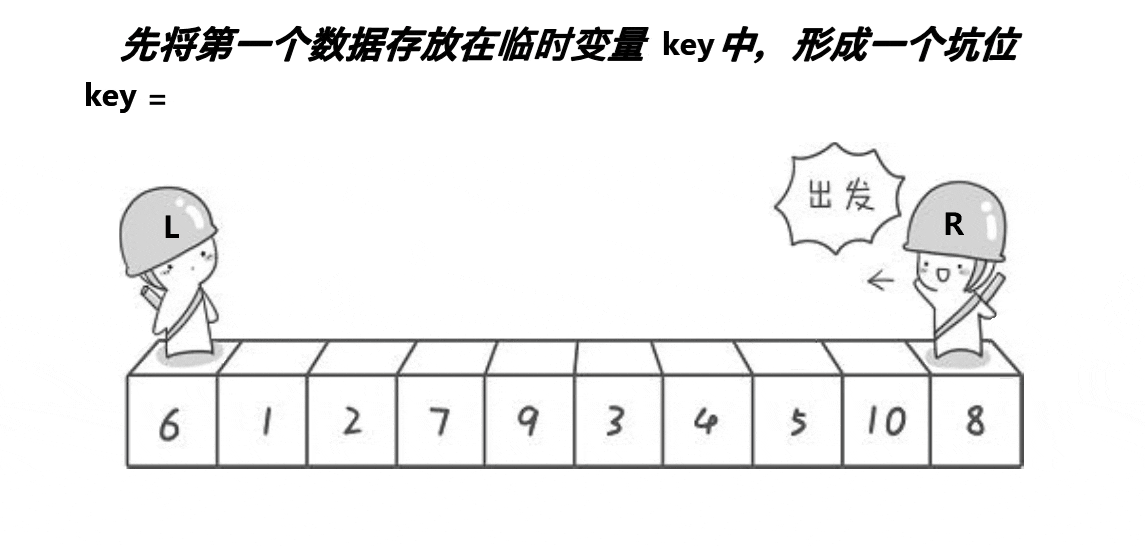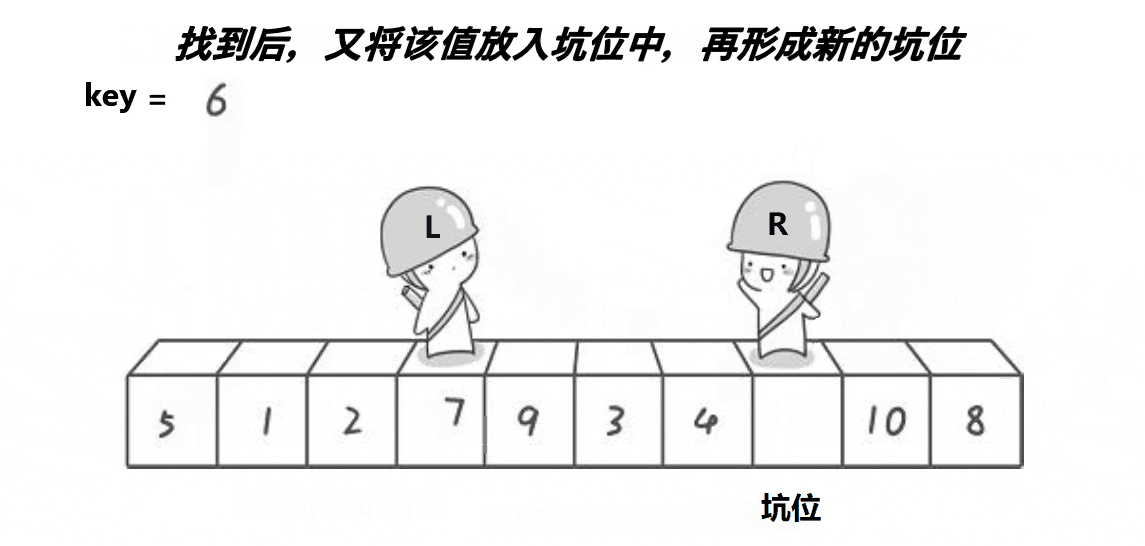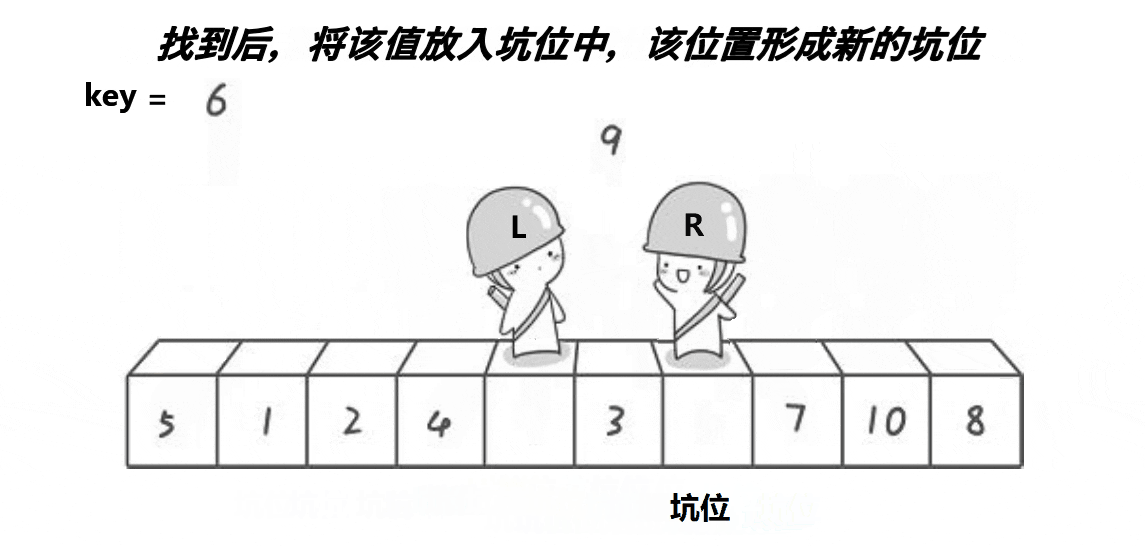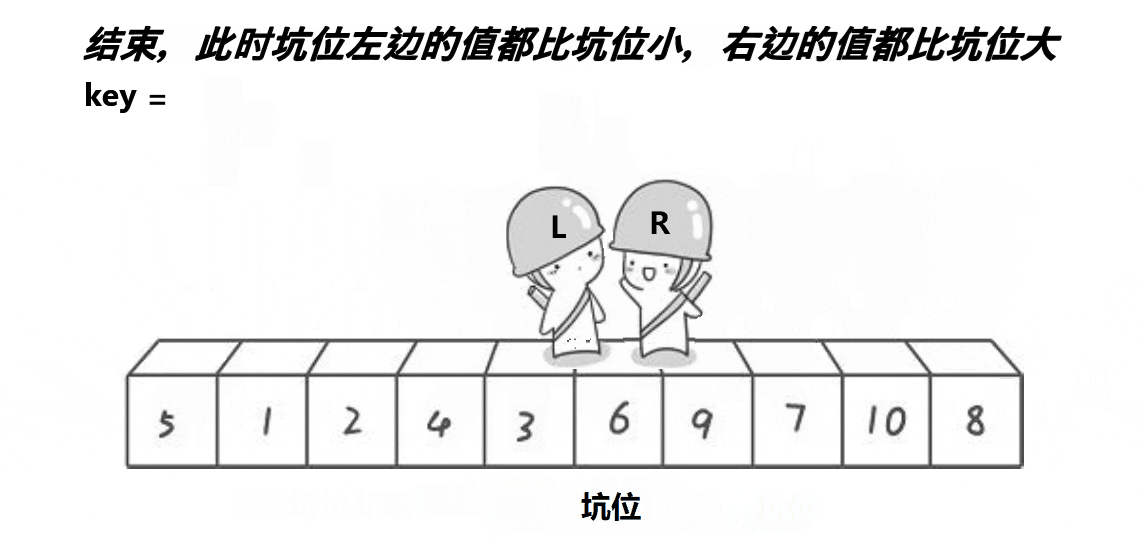
因为有些大佬认为Hoare的方法不易理解,就想到了挖坑法进行,这里用到了坑位
思路:key取出首元素,2个指针;begin指向首位置,end指向尾位置
✨占坑位的不能动,刚开始没有坑位的是end,当end走到比key小的位置,我们将end指向的元素放到begin指向的坑位,此时end变成坑位,end不动,begin走,找到比key大的元素,将begin指向的元素放到end指向的坑位;直到二者相遇,此时一起蹲坑,将key放到坑里面✨
前后指针法:
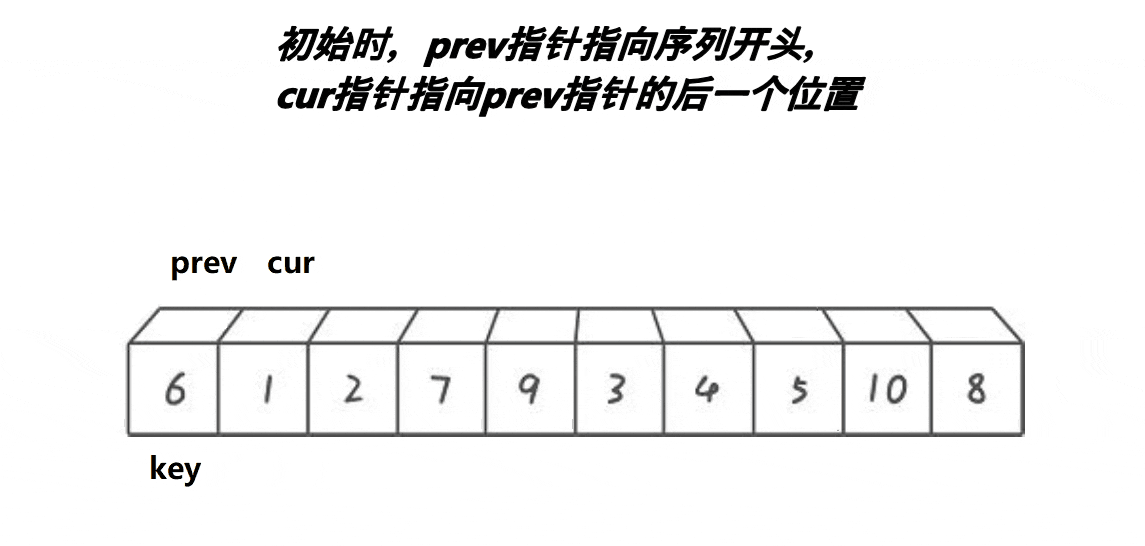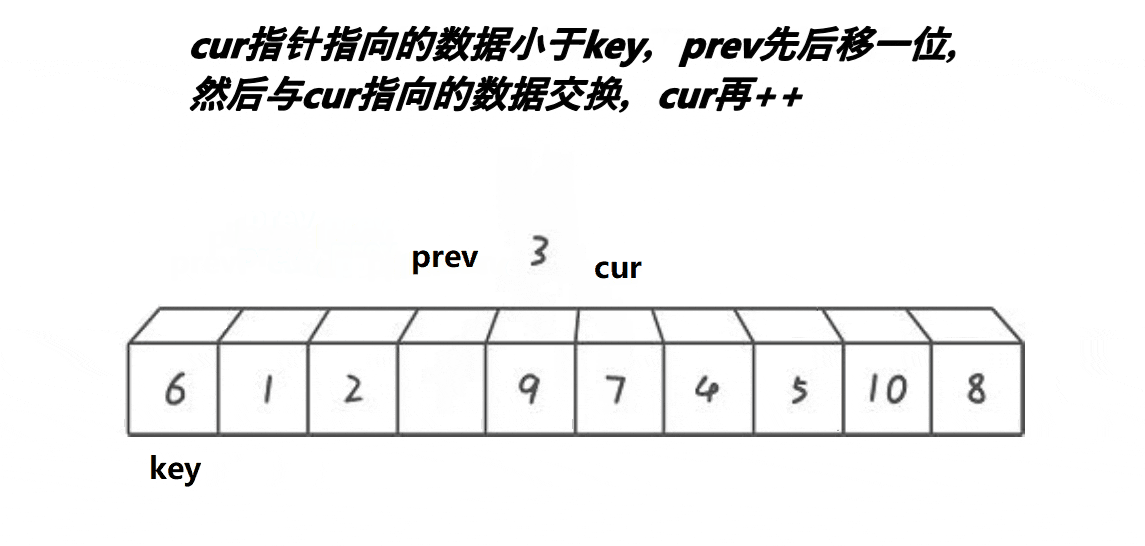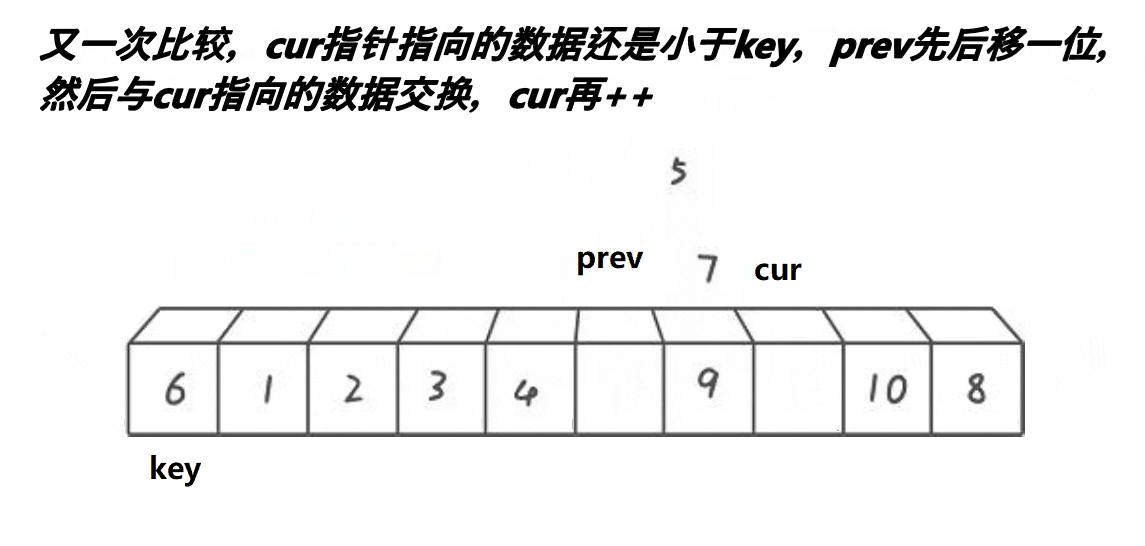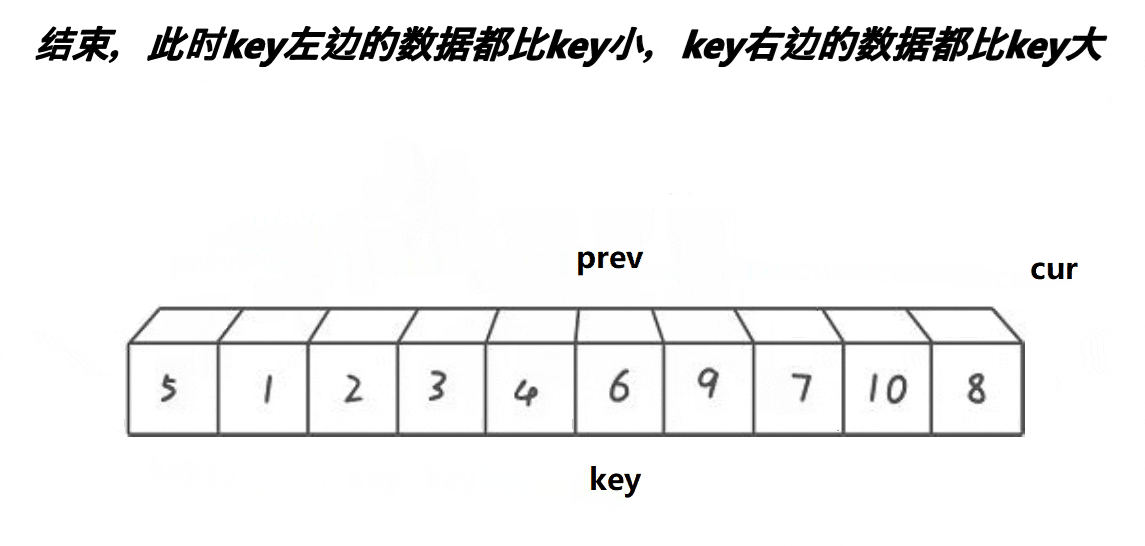
思路:2指针,起始位置:prev指向首元素,cur在第二个元素位置,先让cur走,若是cur指向数据比key小 ,则prev后移动一位,然后将cur指向的元素和prev指向的元素进行交换,当prev走过尾元素,也就是走出区间,将prev的值和key的值进行交换✨
总结:
🧑🎓后面2种写法都没有画过程,看动图其实就能很好的理解哦,很简单的,这里就不要考虑先走的问题了 直接规定好了。🐸当然啦✨✨三种方法的效率是一样的,后面的方法是为了更好的理解Hoare的思想,他们也就只是排序的写法改变了,方式都是一样的,逻辑没变✨
三、非递归思想:
✨我们通过递归可以发现,递归的是区间,对区间进行的修改,那么接下来以下面这个数组作为例子:👉
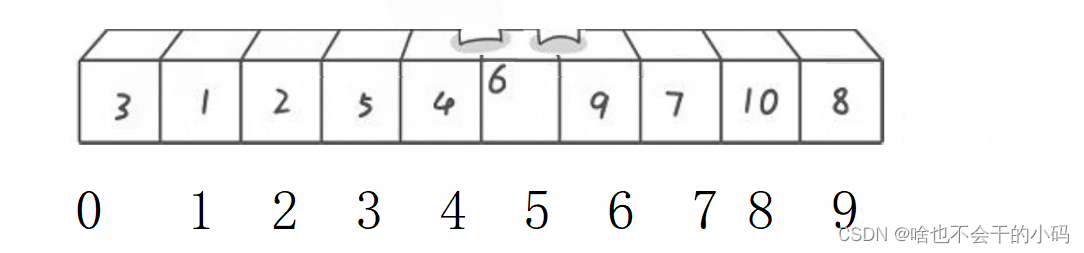
✨ 递归变非递归 其实就是将其变成迭代的思路
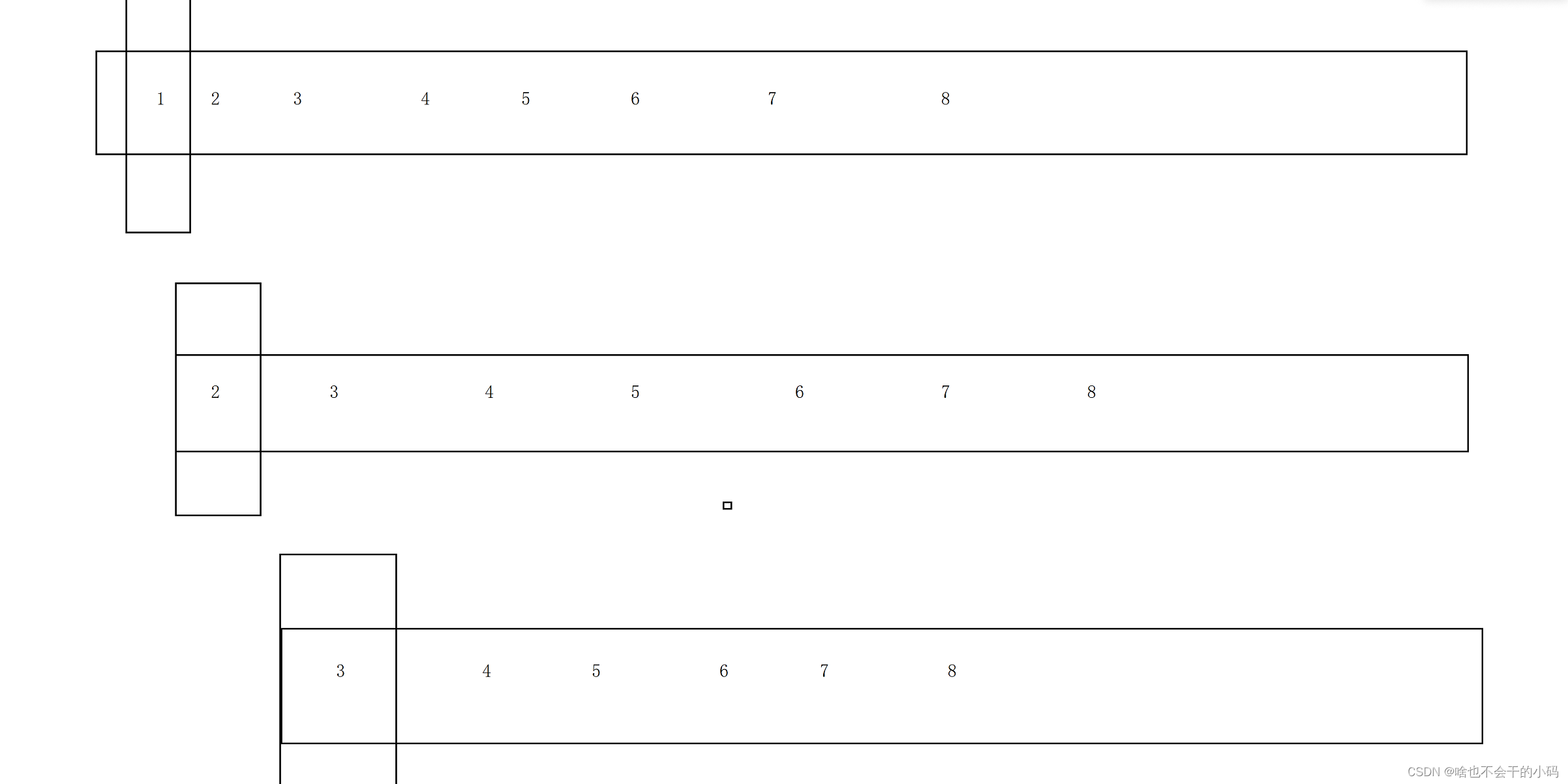
我们二叉树的前序遍历,就是根、左子树、右子树,那么我们的思路就是先遍历[0,9];然后遍历[0,4]再是[0,1] [3,4]等等,那么我们想到了创建一个栈来实现;利用先进后出的特点,可以将区间压进去,先入右区间,再入左,先出来的就是左区间
先入【0.9】 取出来进行排序
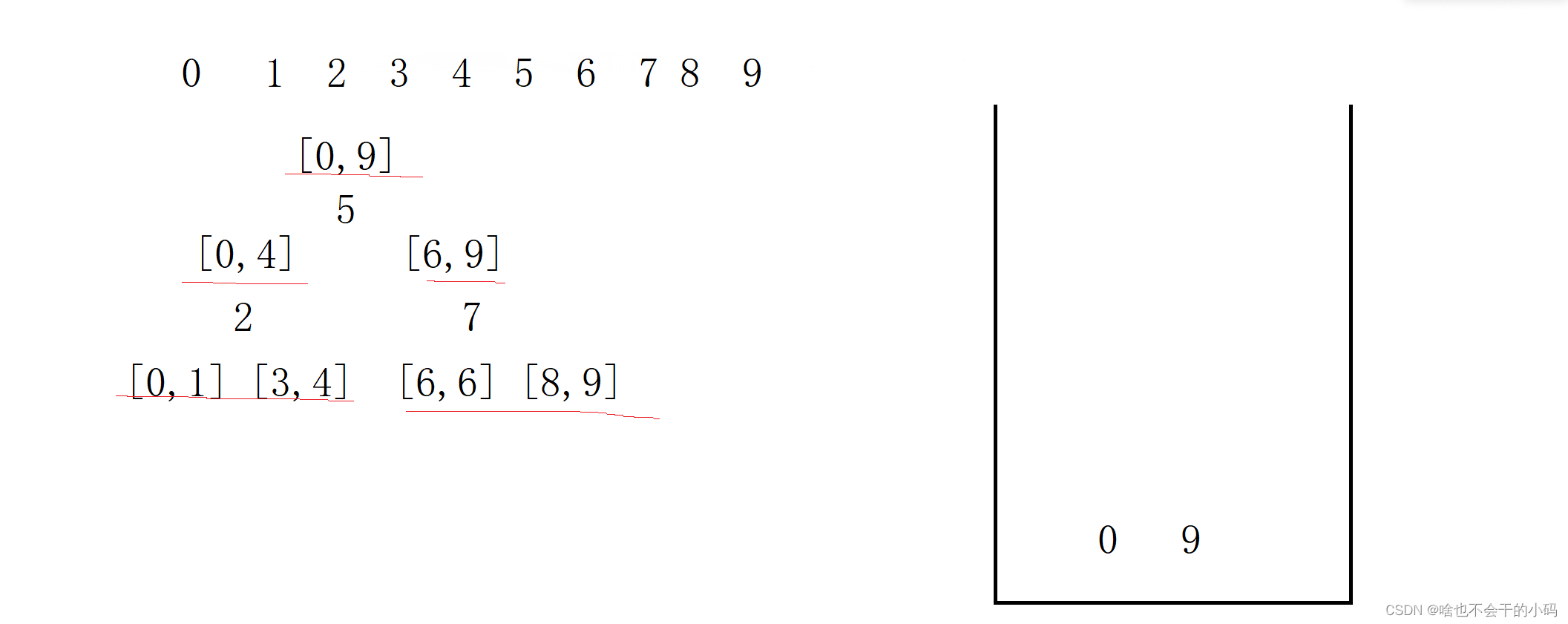
排完以后找到5,然后再入[6,9] 和 [0,4],此时区间变成2部分
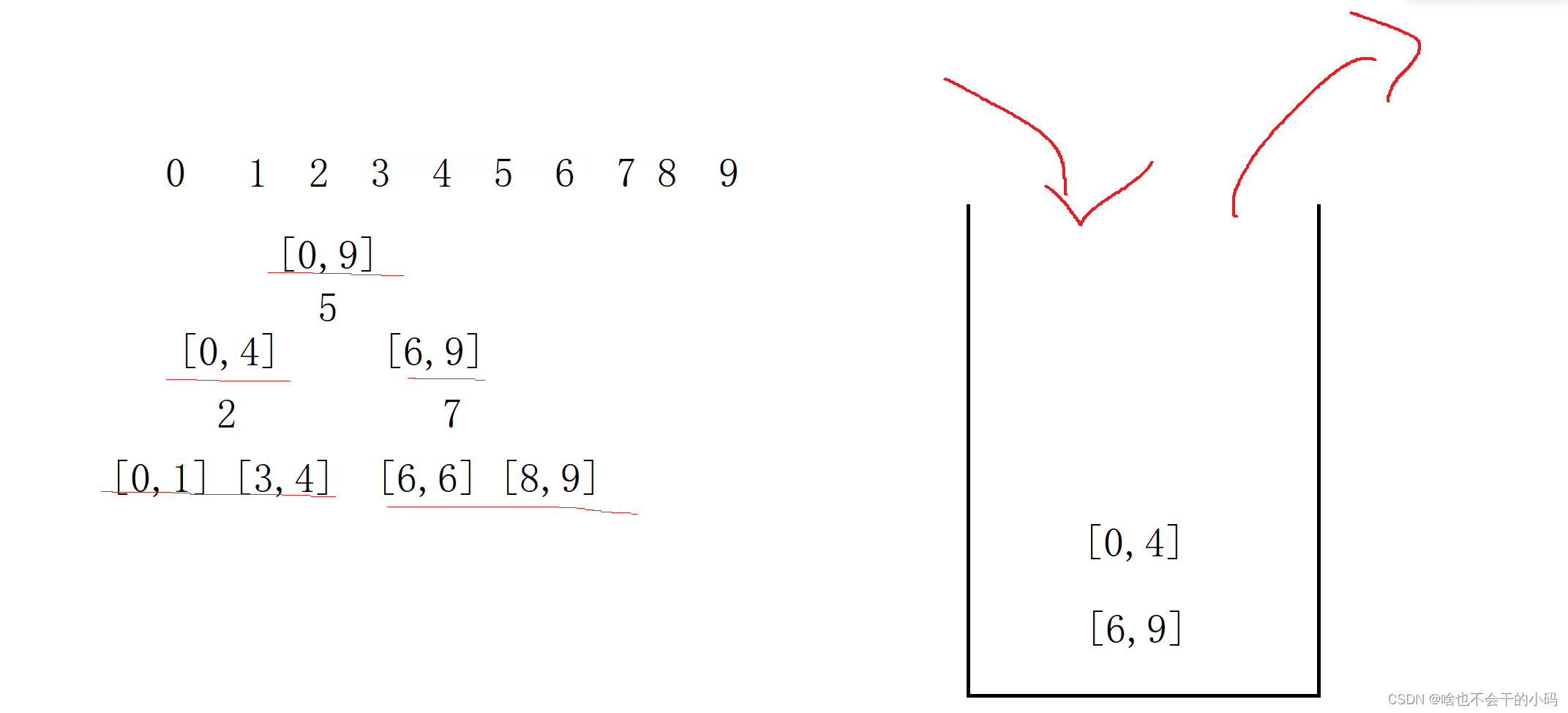
0,4\]出栈,交换后,此时以下标2进行分区间入栈

👉👉👉 是不是很好看懂,就是先动左区间再动右区间,处理一边再处理另一边,其实就是深度优先遍历么🐸🧑🎓
✨结束条件就是空栈结束喽
当然啦,你可以用**队列** 实现,但是要注意队列是**先进先出**,它是一层一层的进行排的
排序的和递归里的排序方法一样,三种方法随便选一个都可以用,我们的**栈就是来模拟实现先序遍历的过程**
## 四、代码实现:
### 优化:三数取中,每种实现方法都需要用这个函数
```cpp
//三数取中
int GetMin(int* a, int left, int right)
{
int min = ((right - left) >> 1)+ left;
if (a[min] < a[left])
{
if (a[min] > a[right])
{
return min;
}
else if (a[right]