数据结构--拓扑排序

一、拓扑排序

对于一个有向无环图G 进行拓扑排序，是将G中所有节点排成一个线性序列，该序列满足以下两个条件：① 每个节点有且仅出现一次 ② 若存在一条从节点A到节点B的路径，则在序列中A一定出现在B前面。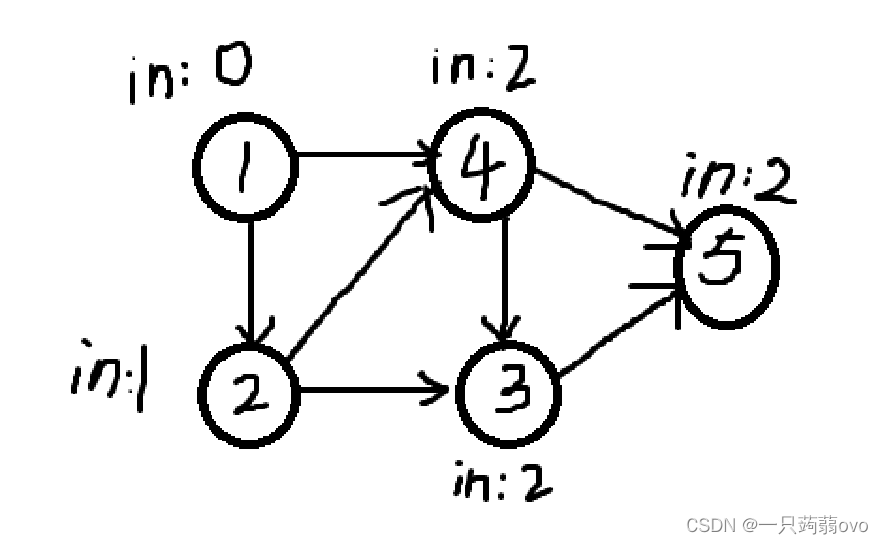

对于求一个有向无环图的拓扑排序步骤：

1.在图中找到一个没有前驱(入度为0)的节点，然后输出

从图中删除该节点和所有以它为起点的有向边**（使边到达的节点 v 的入度-1）**

3.重复操作1和操作2，直到图为空或当前图不存在无前驱的顶点为止**（图存在环）**

第一步操作，删除节点 1

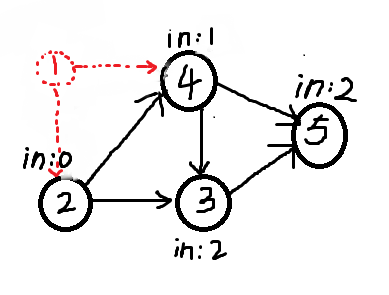
第二步操作，删除节点 2

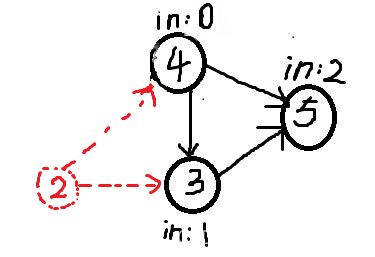
第三步操作，删除节点4

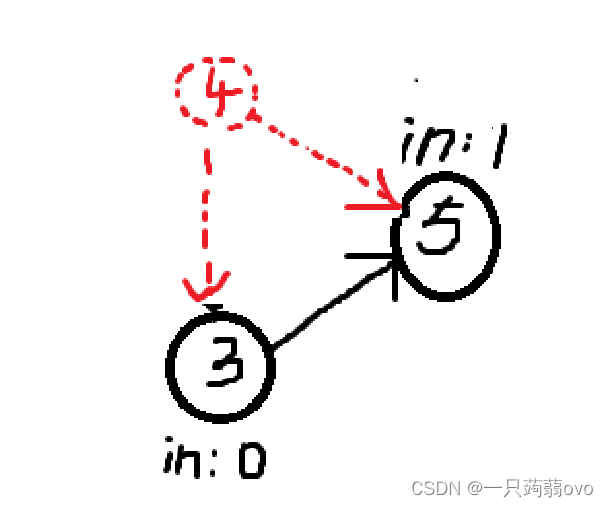
最后拓扑排序依次为 3 5，不再画图讲述。

所以最后拓扑排序的顺序依次为 1 2 4 3 5

二、代码实现拓扑排序

1.Kahn算法

算法思路：与上述实践过程相同

①记录各个点的入度,将入度为0的点加入队列

②依次将队列里的点取出，将以该点为起始点的边，删除边，并将另一侧的入度-1，若此时该点入度为0，则入队

③ 每个节点入队的顺序即为拓扑排序的顺序，若存在某点没有进入过队列，则无法进行拓扑排序

void tuopo()
{
    queue<int>q;
    for(int i=1;i<=n;i++)
        if(in[i]==0) q.push(i);  //将入度为0的点入队列
    while(!q.empty())
    {
        int u=q.front(); q.pop(); // 选一个入度为0的点，出队列
        ans[++sum]=u;
        for(int i=head[u];i!=1;i=edge[i].next)
        {
            int v=egde[i].v;
            in[y]--;
            if(in[y]==0)
                q.push(y); 
        }
    }
}

2. dfs 算法 (实现逆拓扑排序)

根据节点的出度判断，即当节点 x 不能够继续深搜时,加入逆拓扑排序序列中。最后再根据逆拓扑排序序列倒序输出即可。

需要对所有点都深搜一遍.

以例题B3644 【模板】拓扑排序 / 家谱树 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn) 代码如下:

cpp 复制代码

#include<stdio.h>
#include<string.h>
#include<queue>
#include<iostream>
using namespace std;
int head[100001],vis[1001],cnt,ans[1001];
struct node{
	int v,next;
}edge[100001];
queue<int>q;
int in[100001];
void addedge(int u,int v)  // 链式前向星
{
	edge[++cnt].v=v;
	edge[cnt].next=head[u];
	head[u]=cnt;
}
void dfs(int u)
{
	if(vis[u]==1) return ;
	vis[u]=1;
	for(int i=head[u];i!=-1;i=edge[i].next)
	{
		int v=edge[i].v;
		if(!vis[v]) dfs(v); // 没有访问过，深搜
	}
	q.push(u);
	return ;
}
int main()
{
	int n;
	memset(head,-1,sizeof(head)); // 初始化
	scanf("%d",&n);
	for(int i=1;i<=n;i++) //建边  题目要求
	{ 
		int x;
		scanf("%d",&x);
		if(x!=0) addedge(i,x);
		while(x!=0)
		{
			scanf("%d",&x);
			if(x!=0) addedge(i,x);
		}
	}
	int x;
	for(int i=1;i<=n;i++) // 每个点都搜一边，存在多个图的情况
		dfs(x);
	for(int i=1;i<=n;i++)	{ans[i]=q.front();q.pop();}
	for(int i=n;i>=1;i--) printf("%d ",ans[i]);
	return 0;
}