数据结构---外部排序

个人介绍

hello hello~ ，这里是 code袁~💖💖 ，欢迎大家点赞🥳🥳关注💥💥收藏🌹🌹🌹

🦁作者简介 ：一名喜欢分享和记录学习的在校大学生

💥个人主页 ：code袁

💥 个人QQ ：2647996100

🐯 个人wechat：code8896

专栏导航

code袁系列专栏导航
1 .毕业设计与课程设计：本专栏分享一些毕业设计的源码以及项目成果。🥰🥰🥰
2. 微信小程序开发：本专栏从基础到入门的一系开发流程，并且分享了自己在开发中遇到的一系列问题。🤹🤹🤹
3. vue开发系列全程线路：本专栏分享自己的vue的学习历程。

非常期待和您一起在这个小小的互联网世界里共同探索、学习和成长。💝💝💝 ✨✨ 欢迎订阅本专栏 ✨✨

外排序

在计算机科学中，外排序（External Sorting）是一种处理大规模数据的排序算法，通常用于处理无法一次性加载到内存中的数据集。外排序通过在内存和外部存储（如磁盘）之间进行数据交换和排序，以有效地处理大型数据集。以下是关于外排序的学习笔记，包括外排序的原理、实现方式和示例代码：

外排序的原理

1. 分割阶段：将大型数据集分割成适合内存加载的块。
2. 排序阶段：将每个块加载到内存中，在内存中使用常规排序算法（如快速排序、归并排序）对块进行排序。
3. 合并阶段：将排好序的块合并成更大的块，直到整个数据集排序完成。

外排序的实现

外排序通常涉及到内存和外部存储之间的数据交换，需要考虑磁盘I/O的开销和效率。常见的外排序算法包括多路归并排序（Multiway Merge Sort）和置换-选择排序（Replacement Selection Sort）等。

代码示例

以下是一个简单的外排序示例代码，使用Python实现多路归并排序：

import heapq

def external_sort(input_file, output_file, chunk_size):
    with open(input_file, 'r') as f:
        chunk = []
        chunk_count = 0
        while True:
            line = f.readline().strip()
            if not line:
                break
            chunk.append(int(line))
            if len(chunk) == chunk_size:
                chunk.sort()
                with open(f'chunk_{chunk_count}.txt', 'w') as chunk_file:
                    for num in chunk:
                        chunk_file.write(str(num) + '\n')
                chunk_count += 1
                chunk = []
        
        if chunk:
            chunk.sort()
            with open(f'chunk_{chunk_count}.txt', 'w') as chunk_file:
                for num in chunk:
                    chunk_file.write(str(num) + '\n')
            chunk_count += 1

    # 多路归并
    with open(output_file, 'w') as out_f:
        heap = []
        files = [open(f'chunk_{i}.txt', 'r') for i in range(chunk_count)]
        for i, file in enumerate(files):
            num = int(file.readline().strip())
            heapq.heappush(heap, (num, i))

        while heap:
            min_num, file_idx = heapq.heappop(heap)
            out_f.write(str(min_num) + '\n')
            next_num = files[file_idx].readline().strip()
            if next_num:
                heapq.heappush(heap, (int(next_num), file_idx))

        for file in files:
            file.close()

# 示例
external_sort('input.txt', 'output.txt', 1000)

外排序的应用场景

1. 数据库系统中对大型数据表进行排序操作。
2. 处理大规模日志文件或数据备份文件。
3. 处理超出内存容量的数据集。
   优化：多路平衡归并
   若改用4 44路归并排序，则只需2 22趟归并，外部排序时的总读/写次数便减至32 × 2 + 32 = 96 32×2+ 32= 9632×2+32=96。因此，增大归并路数，可减少归并趟数，进而减少总的磁盘I / O I/OI/O次数。

一般地，对r rr个初始归并段，做k kk路平衡归并,归并树可用严格k kk叉树（即只有度为k kk与度为0 00的结点的k kk叉树)来表示。第一趟可将r rr个初始归并段归并为⌈ r / k ⌉ ⌈r/k⌉⌈r/k⌉个归并段，以后每趟归并将m mm个归并段归并成⌈ m / k ⌉ ⌈m/k⌉⌈m/k⌉个归并段，直至最后形成一个大的归并段为止。树的高度 − 1 = ⌈ l o g k r ⌉ = 归并趟数 S 树的高度-1=⌈log_kr⌉=归并趟数S树的高度−1=⌈log

k r⌉=归并趟数S。可见，只要增大归并路数k kk，或减少初始归并段个数r rr，都能减少归并趟数S SS，进而减少读写磁盘的次数，达到提高外部排序速度的目的

置换选择排序（Replacement Selection Sort）是一种外部排序算法，用于对大规模数据进行排序。它通过在内存中维护一个大小为M的最小堆（通常称为置换选择树），并利用置换策略来选择最小元素进行排序。以下是有关置换选择排序的学习笔记，包括算法原理、实现方式和示例代码：

置换选择排序

1. 分割阶段：将大型数据集分割成适合内存加载的块，并在内存中维护一个大小为M的最小堆。
2. 排序阶段：从每个块中选择最小的元素，并将其输出到排序文件中。
3. 置换策略：当最小堆中的元素被选取后，需要从同一块中选择下一个最小元素来填充该位置，以保持最小堆的性质。

置换选择排序的实现

置换选择排序通常需要考虑内存和磁盘I/O之间的数据交换，以及置换策略的选择。下面是一个简单的置换选择排序示例代码，使用Python实现：

import heapq

def replacement_selection_sort(input_file, output_file, block_size):
    with open(input_file, 'r') as f:
        heap = []
        output = []
        block = []
        for line in f:
            block.append(int(line.strip()))
            if len(block) == block_size:
                block.sort()
                output.append(block[0])
                heapq.heappush(heap, (block[1], iter(block[1:])))
                block = []
        
        if block:
            block.sort()
            output.append(block[0])
            heapq.heappush(heap, (block[1], iter(block[1:])))

    with open(output_file, 'w') as out_f:
        while heap:
            min_val, next_val_iter = heapq.heappop(heap)
            output.append(min_val)
            try:
                next_val = next(next_val_iter)
                heapq.heappush(heap, (next_val, next_val_iter))
            except StopIteration:
                pass
        
        for val in output:
            out_f.write(str(val) + '\n')

# 示例
replacement_selection_sort('input.txt', 'output.txt', 1000)

置换选择排序的应用场景

1. 处理大规模数据集的外部排序需求。
2. 数据库系统中对大型数据表进行排序操作。
3. 处理超出内存容量的排序任务。

败者树（Loser Tree）是一种数据结构，通常用于外部排序算法中，特别是多路归并排序中。败者树的主要作用是在多路归并排序过程中快速找到当前最小的元素，并将其输出到排序结果中。以下是有关败者树的学习笔记，包括算法原理、实现方式和示例代码：

败者树

1. 结构特点：败者树是一种完全二叉树，每个非叶子节点保存了其子树中的最小值，而叶子节点保存了数据源中的元素。
2. 初始化：在初始化阶段，败者树的叶子节点被初始化为数据源中的元素，非叶子节点被初始化为一个较大的值（通常为正无穷大）。
3. 选择最小值 ：在多路归并排序过程中，通过比较败者树的根节点和其子节点的值，可以快速找到当前最小的元素。
   1.将每个归并段的第一个元素作为叶子结点加入败者树中
   
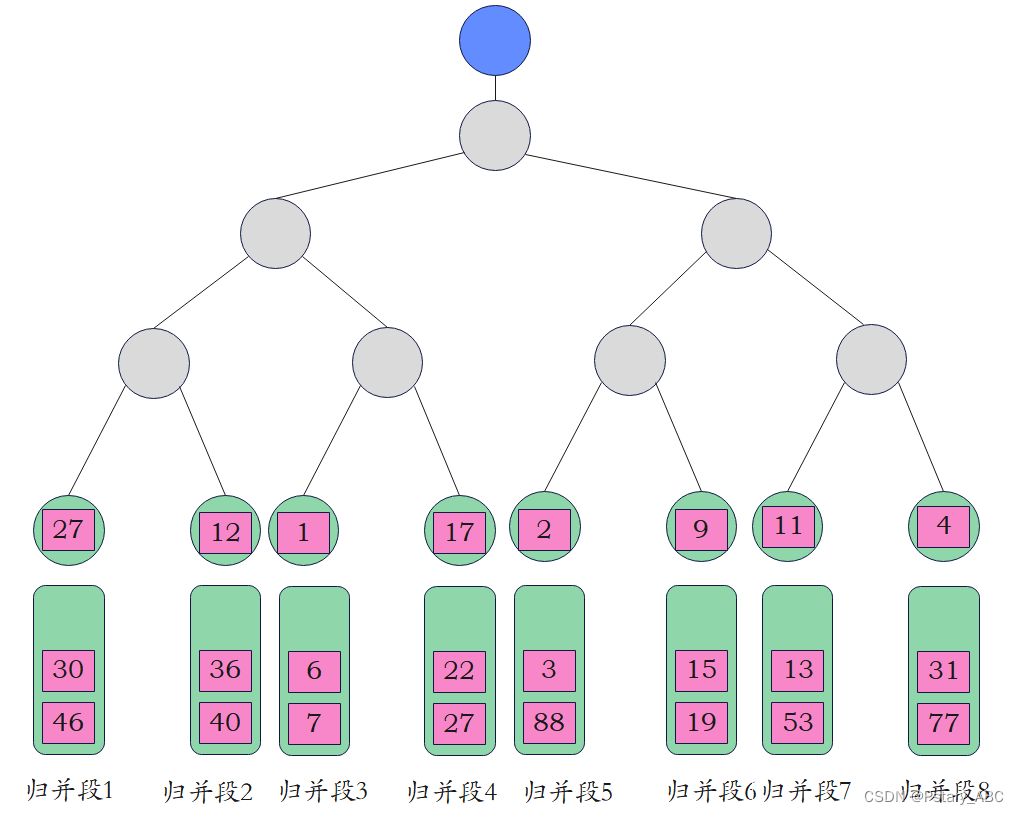
   2.从左至右、从上往下的更新分支节点的信息：判断其左右子树的大小，除了根节点（最上面那个结点）记录冠军来自哪个归并段外，其余各分支节点记录的是失败者来自哪个归并段。
   
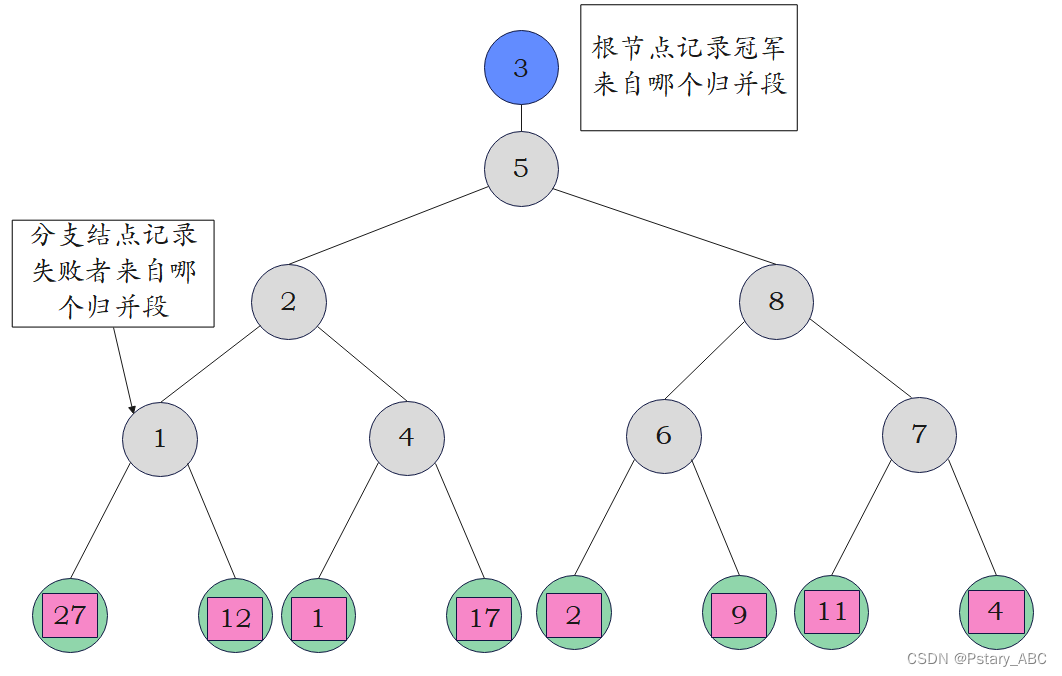
   3.取出最小的元素1 11后，从其所属的归并段中取出下一个元素6 66，依次与从叶子结点到根节点的各个结点所记录的败者信息进行对比。
   

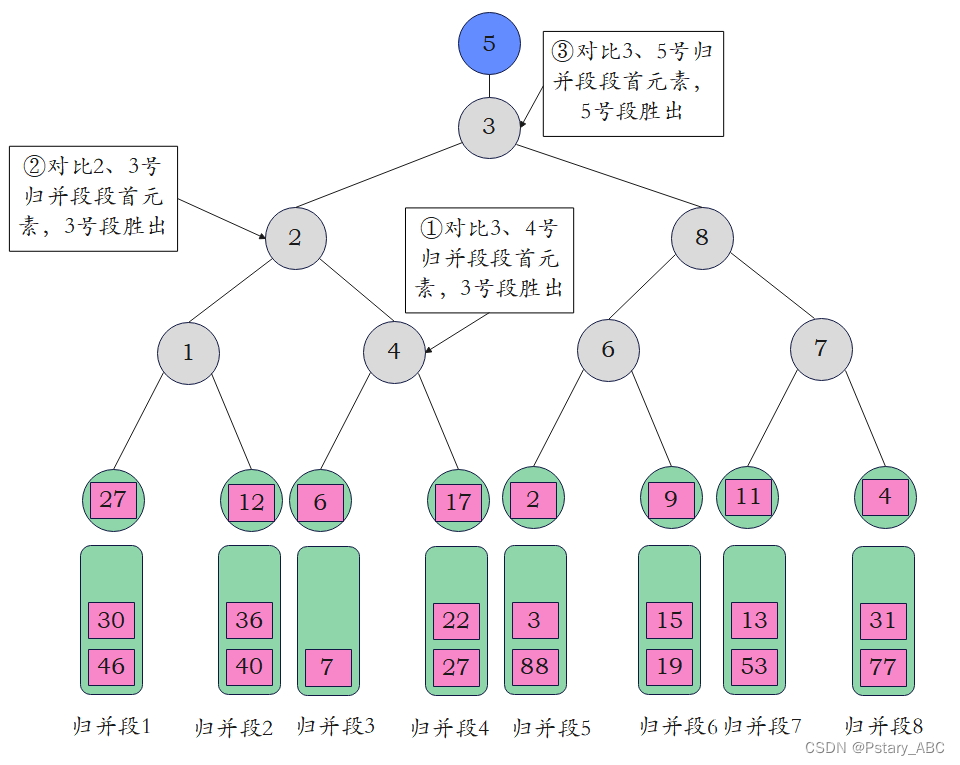
败者树的实现

败者树的实现通常需要考虑如何构建树结构、更新最小值以及输出排序结果。下面是一个简单的败者树示例代码，使用Python实现：

class LoserTree:
    def __init__(self, data):
        self.data = data
        self.tree = [float('inf')] * (2 * len(data))
        self.leaves = len(data)
        self.build_tree()

    def build_tree(self):
        for i in range(self.leaves):
            self.tree[i + self.leaves] = i
        
        for i in range(self.leaves - 1, 0, -1):
            self.tree[i] = self.compete(i)

    def compete(self, idx):
        while idx < self.leaves:
            left = idx * 2
            right = idx * 2 + 1
            if self.tree[idx] == -1 or (self.tree[left] != -1 and self.data[self.tree[left]] < self.data[self.tree[idx]]):
                idx = left
            if right < 2 * self.leaves and (self.tree[idx] == -1 or (self.tree[right] != -1 and self.data[self.tree[right]] < self.data[self.tree[idx]])):
                idx = right
            self.tree[idx // 2] = idx
            idx //= 2
        return self.tree[idx]

# 示例
data = [3, 1, 4, 1, 5, 9, 2, 6]
loser_tree = LoserTree(data)
print([data[loser_tree.tree[1]] for _ in range(len(data))])

败者树的应用场景

1. 在外部排序算法中，如多路归并排序，用于快速找到当前最小的元素。
2. 处理大规模数据集的排序需求，特别是需要大量磁盘I/O的情况下。

注：参考文章

🎉写在最后

🍻伙伴们，如果你已经看到了这里，觉得这篇文章有帮助到你的话不妨点赞👍或 Star ✨支持一下哦！手动码字，如有错误，欢迎在评论区指正💬~

你的支持就是我更新的最大动力💪~