【数据结构】从基础到实战：全面解析归并排序与计数排序

专栏引入

哈喽大家好，我是野生的编程萌新，首先感谢大家的观看。数据结构的学习者大多有这样的想法：数据结构很重要，一定要学好，但数据结构比较抽象，有些算法理解起来很困难，学的很累。我想让大家知道的是：数据结构非常有趣，很多算法是智慧的结晶，我希望大家在学习数据结构的过程是一种愉悦的心情感受。因此我开创了《数据结构》专栏，在这里我将把数据结构内容以有趣易懂的方式展现给大家。

1.归并排序

1.1归并排序的引入

为了引入让大家理解归并排序，首先举一个例子让大家对归并排序有个了解：就以最近结束的高考为例子吧，出分的时候大家都会有一个全省排名，这个全省排名是怎么来的呢？其实也就是每个市、每个县、每个学校的排名合并后得到的。这里我提到了合并一词，我们比较两个同学的成绩很简单，比如甲比乙分数低，丙比丁分数低，那么我们就很容易得到甲乙丙丁合并后的成绩排名，同样的戊己庚辛的排名也可以很轻松的得到，由于他们两组分别有序了，把他们八个的成绩合并有序也是很容易得到的，继续下去....我们可以很轻松的得到班级排名，为了更清晰的理解这里的思想我们看下面的图（画的不好，请多担待）：

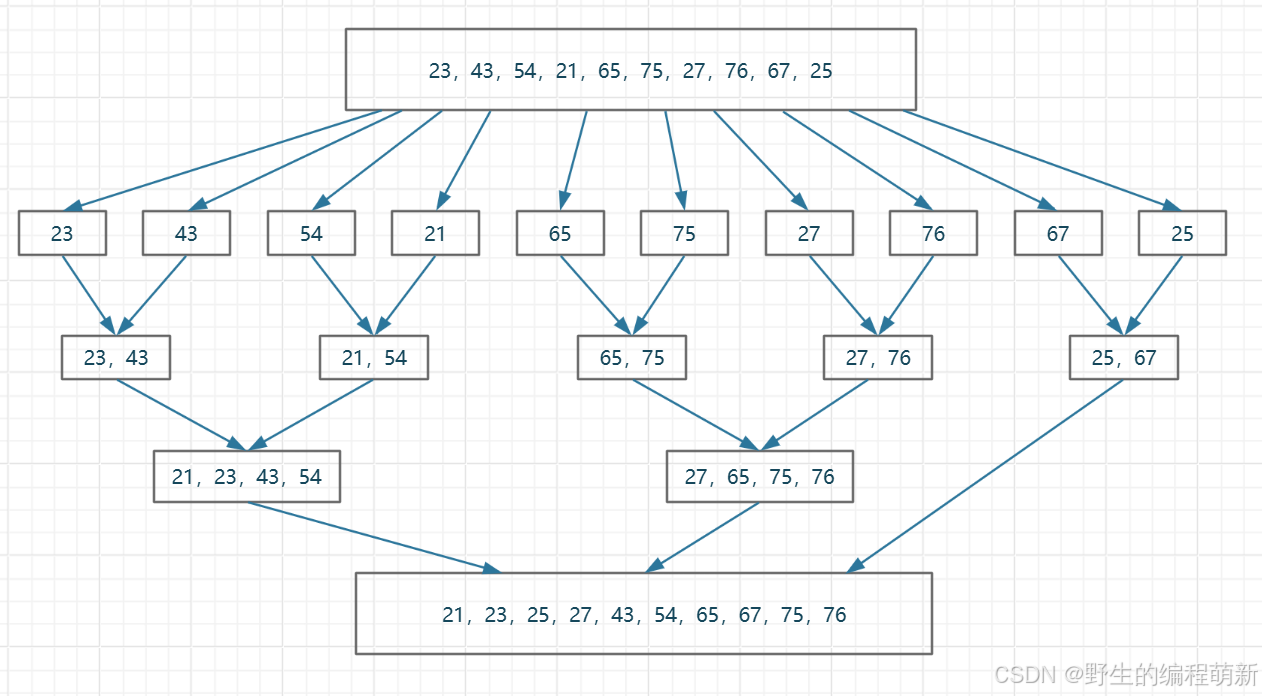
大家仔细观察它的形象，你会发现他像极了满二叉树，通常涉及满二叉树（尤其是完全二叉树）结构的算法效率都不会低---这就是我们要说的归并排序算法。归并一词的中文含义就是合并、并入的意思，而在数据结构中的定义就是将两个或两个以上的有序表组合成一个新的有序表，归并排序的原理就是：**假设初始待排序的序列有n个元素，就可以看成n个长度为1的子序列，然后两两归并，如此重复，知道获得一个长度为n的有序序列为止。**我们来看下面一小段视频更加深入的了解一下归并排序是如何工作的：

归并排序

1.2归并排序的实现

知道了归并排序的核心思想及其工作原理，我们就来实现一下吧：

复制代码

void _Mergesort(int* a, int left, int right, int* tmp)
{
	if (left >= right)
		return;
	int mid = (left + right) / 2;
    //划分成[left,mid]和[mid+1,right]两个区间进行递归
	_Mergesort(a, left, mid, tmp);//左递归
	_Mergesort(a, mid + 1, right, tmp);//右递归

	int begin1 = left, end1 = mid;
	int begin2 = mid + 1, end2 = right;
	int index = begin1;
	while (begin1 <= end1 && begin2 <= end2)
	{
		if (a[begin1] < a[begin2])
			tmp[index++] = a[begin1++];
		else
			tmp[index++] = a[begin2++];
	}
	while (begin1 <= end1)
	{
		tmp[index++] = a[begin1++];
	}
	while (begin2 <= end2)
	{
		tmp[index++] = a[begin2++];
	}
	for (int i = left; i <= right; i++)
	{
		a[i] = tmp[i];
	}
}
void Mergesort(int* a, int n)
{
	int* tmp = (int*)malloc(sizeof(int) * n);
	_Mergesort(a,0,n-1,tmp);
	free(tmp);
	tmp = NULL;
}

这段代码包含两个函数：合并逻辑函数和主函数。合并逻辑负责将两个有序的子数组合并成一个有序的数组。代码中的三个while循环和一个for循环完成了这一任务。第一个while循环: 同时遍历两个子数组（由begin1-end1和begin2-end2定义），比较它们的当前元素，将较小的元素放入临时数组tmp中。这个过程一直持续到其中一个子数组的元素全部被放入tmp中为止。第二个和第三个while循环是将剩余的一个子数组的元素直接复制到tmp中，因为另一个子数组已经是有序的了，所以可以直接复制到tmp中，for循环是将合并后的有序数组复制到原数组a之中。

主函数Mergesort负责管理内存和调用递归。使用malloc函数申请一个大小为n的临时数组太没品，用于在合并时存储有序的数组，调用递归函数_Mergesort函数对整个数组a进行排序，排序完成之后释放掉临时数组tmp的内存，防止野指针的产生。

1.3归并排序的时间复杂度分析

又到熟悉的环节了，先跑1w个数组看看情况如何：

归并排序我们主要从两个阶段来分析：分解阶段和合并阶段。将数组拆分为两个子数组，两个子数组的长度均为n/2，因此两个子问题的时间为2*T(n/2)，合并两个长度为n/2的有序子数组时，需遍历所有n个元素（每个元素仅需比较 1 次、移动 1 次），时间为O(n)。递归树的层数由 "分解终止条件" 决定：当子数组长度为 1 时（n/2^k = 1），分解停止。求解n/2^k = 1→2^k = n→k = log₂n。因此，递归树从根节点（第 0 层）到叶子节点（第log₂n层）共log₂n + 1层（含首尾）。

总时间 = 每层代价 × 层数 = n*(log₂n + 1) = O(n log n)

2.计数排序

2.1计数排序的引入

当我们面对大量数据时，选择合适的排序算法至关重要。传统的比较排序算法，如快速排序和归并排序，虽然在大多数情况下表现优异，但它们的时间复杂度下限为O(n log n)。然而，在某些特殊情况下，我们可以利用数据的特性，设计出时间复杂度为O(n)的排序算法，计数排序（Counting Sort）就是其中之一。计数排序通过计数每个元素出现的次数，然后根据这些计数信息直接确定元素的排序位置，从而实现了线性时间复杂度。在接下来的内容中，我们将深入探讨计数排序的原理、实现步骤及其适用场景。我们先看下面一小段视频来了解一下计数排序：

计数排序

计数排序的核心思想：通过计数每个元素出现的次数，直接确定每个元素在输出数组中的位置。与基于比较的排序算法不同，计数排序利用了键值的整数性质，能够在线性时间内完成排序。

2.1计数排序的实现

我们看下面这段代码：

复制代码

#include <stdio.h>
#include <stdlib.h>

void countingSort(int arr[], int n) {
    int i, max, min;

    // 找到最大值和最小值
    max = arr[0];
    min = arr[0];
    for (i = 1; i < n; i++) {
        if (arr[i] > max)
            max = arr[i];
        if (arr[i] < min)
            min = arr[i];
    }

    // 创建计数数组
    int range = max - min + 1;
    int *count = (int *)calloc(range, sizeof(int));

    // 统计每个元素的出现次数
    for (i = 0; i < n; i++)
        count[arr[i] - min]++;

    // 累加计数数组
    for (i = 1; i < range; i++)
        count[i] += count[i - 1];

    // 构建输出数组
    int *output = (int *)malloc(n * sizeof(int));
    for (i = n - 1; i >= 0; i--) {
        output[count[arr[i] - min] - 1] = arr[i];
        count[arr[i] - min]--;
    }

    // 复制输出数组到原数组
    for (i = 0; i < n; i++) {
        arr[i] = output[i];
    }

    // 释放内存
    free(count);
    free(output);
}

int main() {
    int arr[] = {4, 2, 2, 8, 3, 3, 1};
    int n = sizeof(arr) / sizeof(arr[0]);
    countingSort(arr, n);
    printf("Sorted array: \n");
    for (int i = 0; i < n; i++)
        printf("%d ", arr[i]);
    printf("\n");
    return 0;
}

计数排序的操作步骤：

首先，遍历输入数组，找到其中的最大值max和最小值min。这一步的目的是确定计数数组的大小。
根据max和min的值，创建一个大小为max - min + 1的计数数组count。初始化count数组的所有元素为0。
遍历输入数组，对于数组中的每个元素x，将count[x - min]的值加1。这样，count数组的每个位置就存储了对应元素在输入数组中出现的次数。
对count数组进行处理，使得count[i]存储的是小于等于i + min的元素的个数。这一步通过累加count数组中的值来实现。累加后的count数组可以帮助确定每个元素在排序后数组中的确切位置。
创建一个与输入数组大小相同的输出数组output。然后，逆序遍历输入数组，对于每个元素x，将其放置在output[count[x - min] - 1]的位置上，并将count[x - min]的值减1。这保证了排序的稳定性（即相同元素的相对顺序不变）。
最后，将output数组的内容复制回输入数组，完成排序。

计数排序的使用场景要求元素范围i有限，我们极少数情况下会使用，我们就不在深入的讨论了。