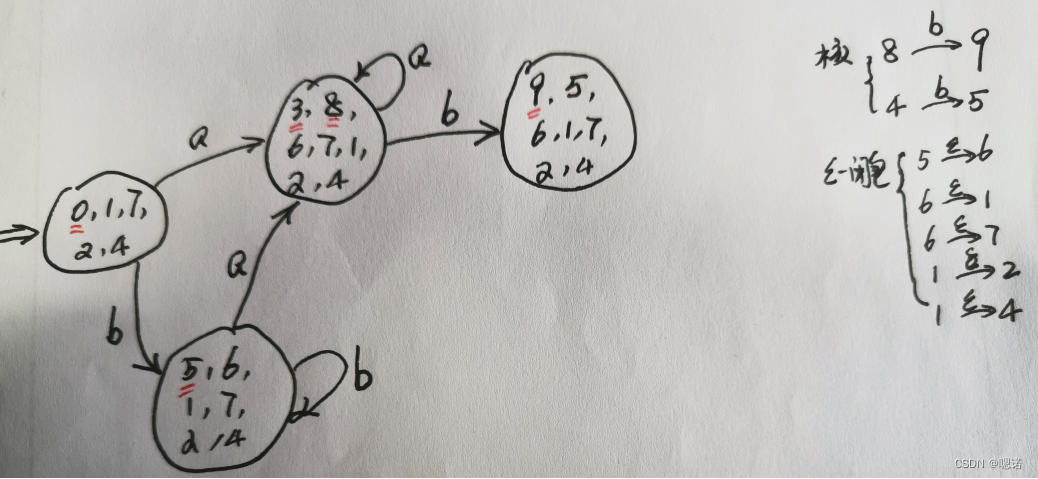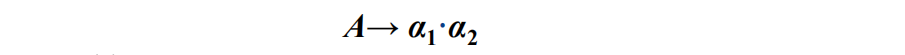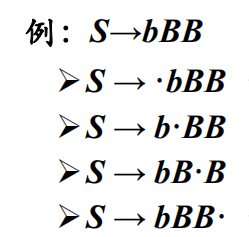一,求表达式的逆波兰式
1,遇到字母直接写到答案中
2,遇到符号加入栈中
3,左括号优先级最低直接进栈,只有遇到成对括号才出栈;逆波兰式不需要括号
4,新加入的符号与栈中符号比较,如果前者优先级要高于原站顶等级则加入栈中,否则栈中符号先出栈(包括优先级低于和等于两种情况)
1.a+b*(c/d+g)
a #(表示栈顶)
a #+
ab #+
ab #+*
ab #+*(
abc #+*(
abc #+*(/
abcd/ #+*(+
abcd/g #+*(+
abcd/g #+*(+)
abcd/g+ #+*遇到括号直接把整个括号中的符号写入答案,注意的是()不写
abcd/g+*+ #剩余符号全部出栈
2.A+B*(C-D)+F/(C-D)^N (^表示指数)
A #
A #+
AB #+*
AB #+*(
ABC #+*(-
ABCD #+*(-
ABCD #+*(-) 、ABCD- #+*
ABCD-*+ #+
ABCD-*+F #+
ABCD-*+F #+/
ABCD-*+F #+/(
ABCD-*+FC #+/(
ABCD-*+FC #+/(-
ABCD-*+FC #+/(-)、ABCD-*+FC- #+/
ABCD-*+FC- #+/^
ABCD-*+FC-N #+/^
ABCD-*+FC-N^/+ #
二、根据文法G写出L([G])
前导知识:
在文法的每一条表达式中,大写字母是非终结符、小写字母是终结符,箭头定义为"="。语言是句子的集合,句子是特殊句型。
如果 S⇒* α,α∈(VT∪VN)*,则称α是G的一个句型。一个句型中既可以包含终结符,又可以包含非终结符,也可能是空串。
如果 S⇒* w,w ∈VT*,则称w是G的一个句子(sentence)。句子是不包含非终结符的句型。
例题1
G[N]:
N->D|ND
D->0|1|2|3|4|5|6|7|8|9
问G[N]的语言是什么?
通过观察,发现第一个表达式出现了直接左递归N=>ND=>NDD=>NDDD......=>D...DDDD
所以N=>D的N次方(得到了一个句型)
代入第二条表达式,分别取n=1,2,3....
发现得到的是D的正闭包(从相同的地方取不一样的个数),也可以写成G[N]=D^n(n>=1)
例题2
G[N]:
Z->aZb
Z->ab
问L(G[N])的全部元素
通过观察,发现第一个表达式出现了递归Z=>aZb=>aaZbb=>aaaZbbb......=>a...aaabbb...b
所以Z=>a^n b^n(句子)
L(G[N])={a^n b^n | n>=1},(句子的集合就是语言)
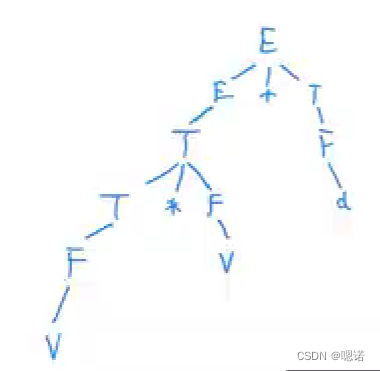
三、分析句型构造语法树、写出短语、直接短语和句柄
例题1:
令文法G[E]为:
E->E+T | T
T-> T*F | F
F->(E)|v|d
(1)分析说明v*v+d是它的一个句型
(2)指出这个句型的所有短语、直接短语和句柄
(1)证明是否是一文法的句型,最简单的证明方法是画出语法树
第二种方法是使用最左推导或者最右推导或者混合使用
E=>E+T =>T+T=>T*F+T=>F*F+T=>v*F+T=>v*v+F=>v*v+d
按照上面的推导可以从上到下画一颗语法树
(2)
技巧:只看所有非叶子节点,从最后一层往上看,把根的叶子进行组合;只看所有非叶子节点,在同一层,从左往右看
解答如下:
先圈出所有非叶子节点
最后一层是F,所以短语有v
倒数第二层是T和F;因为T的叶子节点跟最后一层的重复了,所以不写;然后看F,F底下有个叶子节点v,所以现在短语是v,v
倒数第三层也是T和F;这个T的叶子结点则是v*v;F的叶子节点则是d;所以现在短语是v,v,v*v,d
倒数第四层是E和T;E的叶子结点和T是一样的,都是v*v,所以不重复写了;T的叶子结点和F一样都是d ,也不重复写;所以现在短语是v,v,v*v,d
最后一层也是根节点;它的叶子结点是v*v+d;所以现在短语是v,v,v*v,d,v*v+d
综上:所有短语是v,v,v*v,d,v*v+d
直接短语就是高度为一的短语,比如F-v,F-v,F-d;最左边的那个T的叶子节点虽然也是v,但是是经过两层的,所以不是直接短语。
综上:直接短语是v,v,d(按顺序写上)
句柄就是写好的直接短语中最左边的那个也就是第一个
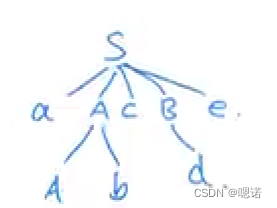
例题2:
令文法G[S]为:
S->aAcBe
A->b|Ab
B->d
(1)分析说明aAbcde是它的一个句型
(2)指出这个句型的所有短语,直接短语和句柄
(1)S=>aAcBe=>aAbcBe=>aAbcde
(2)
先圈出所有非叶子节点:
倒数第一层有A,B;A的叶子有Ab;B的叶子是d;所以现在短语有Ab,d;
根节点有S;S的叶子是aAbcde;所以短语有Ab,d,aAbcde
综上,短语有Ab,d,aAbcde,直接短语有Ab,d,
例题3:
令文法G[S]为:
S->SS*
S->SS+
S->a
(1)分析说明aa+a*是它的一个句型
(2)指出这个句型的所有短语,直接短语和句柄
(1)
S=>SS*=>SS+S*=>aS+S*=>aa+S*=>aa+a*
(2)
圈出所有非终结符之后开始解题:
共三层,倒数第一层是S和S;第一个S的短语和第二个短语均是a;所以短语是a,a
倒数第二层是S和S;第一个S的短语是aa+;第二个S的短语是a
最后一层短语是aa+a*
综上:短语有a,a,aa+,a,aa+a*;直接短语有a,a,a;句柄是最左边的a
四、正规式转正规文法
将正规式
r转换为正规文法G,核心是将正规式拆分为正规文法的多个产生式,这是一个由一到多 的过程。正规文法最终必须有一个开始符号,于是我们选定S作为开始符号,令S → r,然后逐步对r进行拆分,生成多个产生式。拆分规则如下:
A → xy可拆分为A → xB,B → yA → x*y可拆分为A → xA,A → yA → x|y可拆分为A → x,A → y对于规则二,实际我们知道
x*y是形如xxxxxxy的,所以需要进行循环替换,必须有A → xA;符号串最后有个y,所以必须有A → y。
例题:
将正规式r=a(a|d)*转为相应的正规文法G[s]:
1.设开始符号为S,则S->a(a|d)*
2.使用规则1:S->aA A->(a|d)*
3.对第2步的第2个式子使用规则2展开:A->(a|d)A A->ε
4.对第三步的第一个式子可以换成A->aA|dA,使用规则3 可得:A->aA,A->dA
5.综上:
G[S]:
S->aA,A->aA,A->d,AA->ε
五、正规文法转正规式
基本为上一题型反过来罢了:
- (1)A->xB, B->y对应A->xy(产生式有非终结符且该非终结符不等于产生式的左边)
- (2)A->xA, A->y对应A->x*y(产生式有非终结符且该非终结符等于产生式的左边)
- (3)A->x, A->y对应A->x|y(产生式没有非终结符)
例题:
文法G[S]:
(1)S->aA
(2)S->a
(3)A->aA
(4)A->dA
(5)A->a
(6)A->d
转换为正规式:
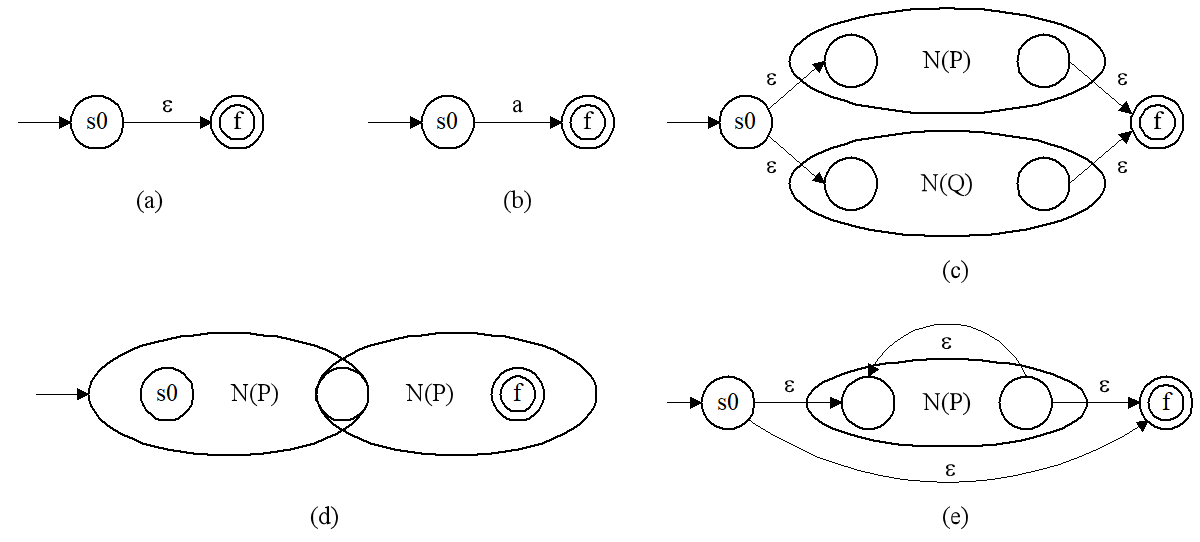
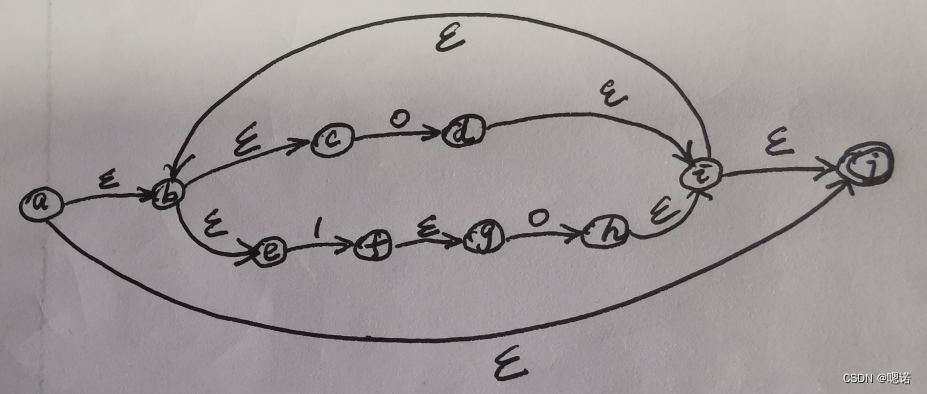
六、正规式转NFA
规则:
① 对ε,构造NFA如图(a)所示。其中,s0为初态,f为终态,该NFA接受ε;
② 对∑上的每一个字符a,构造NFA如图(b)所示。其中,s0为初态,f为终态,该NFA接受{a};
③ 若N(p)和N(q)是正规式p和q的NFA,则:
(a) 对正规式p|q,构造NFA如图(c)所示。其中,s0为初态,f为终态,该NFA接受L(p)∪L(q);
(b) 对正规式pq,构造NFA如图(d)所示。其中,s0为初态,f为终态,该NFA接受L(p)L(q);
(c) 对正规式p*,构造NFA如图(e)所示。其中,s0为初态,f为终态,该NFA接受L(p*)。
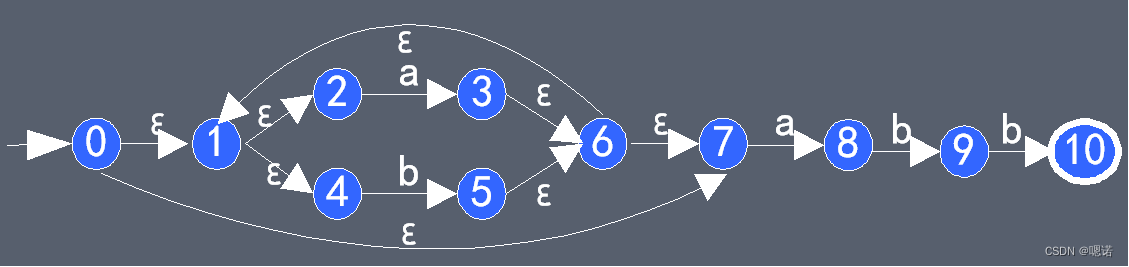
例题1:
将正规式r=(a|b)*abb构造成NFA:
例题2:
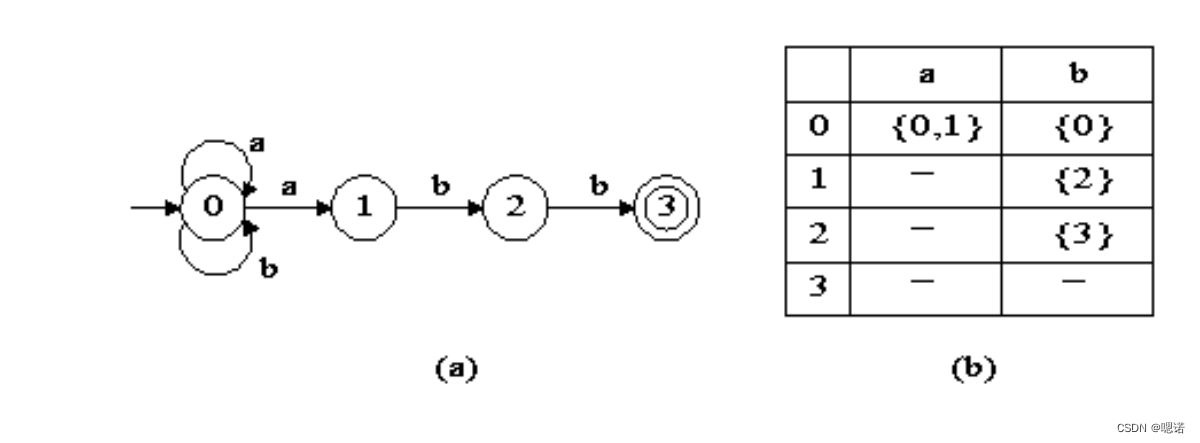
识别由正规式(a|b)*abb说明的记号的NFA定义如下:
S={0,1,2,3}, Σ={a,b}, s0 = 0, F={3}
move = { move(0,a)=0, move(0,a)=1, move(0,b)=0, move(1,b)=2, move(2,b)=3}
所得状态转换图和状态转换矩阵NFA如下:
上图为识别(a|b)*abb的NFA
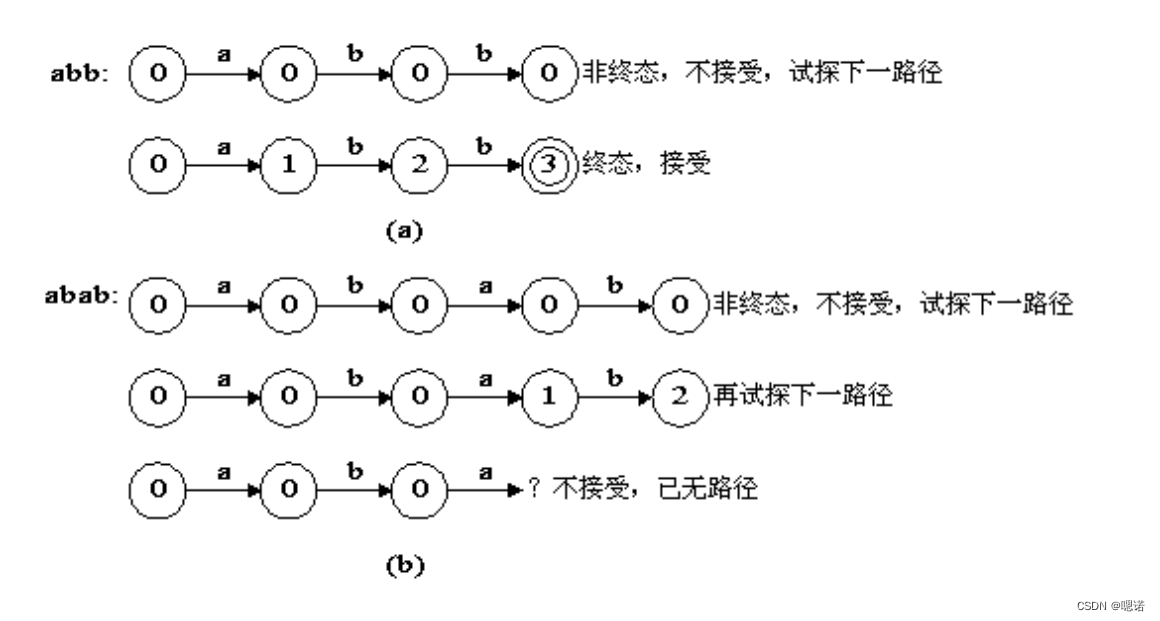
用上图的NFA识别输入序列abb和abab
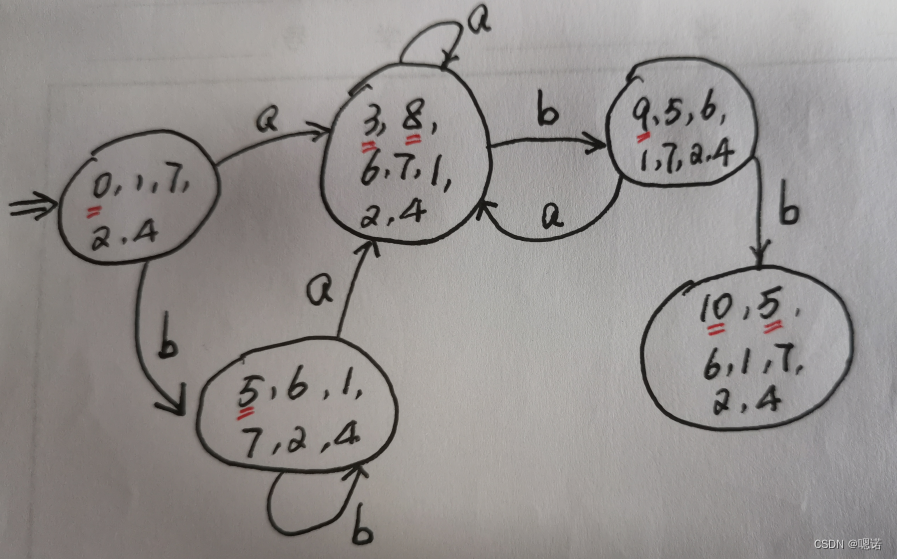
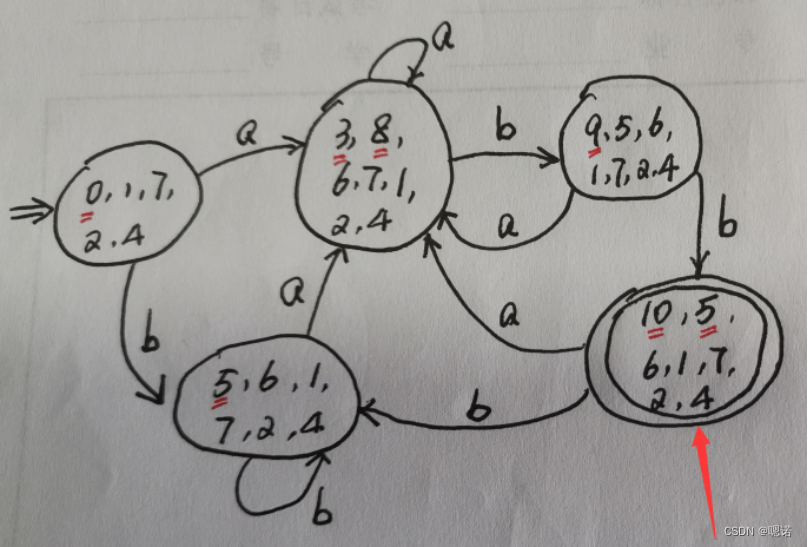
七、NFA转DFA
子集法例题:
将正规式r=(a|b)*abb构造成NFA转为DFA
解答:
状态集中如果包含NFA中的终态,该状态集也为DFA的终态
综合例题
语言Σ={0,1}上所有满足如下条件的字符串:
每个1都有0直接跟在右边
(1)构造正规式
正规式:(0|10)*
(2)用Thompson算法将其转换为NFA
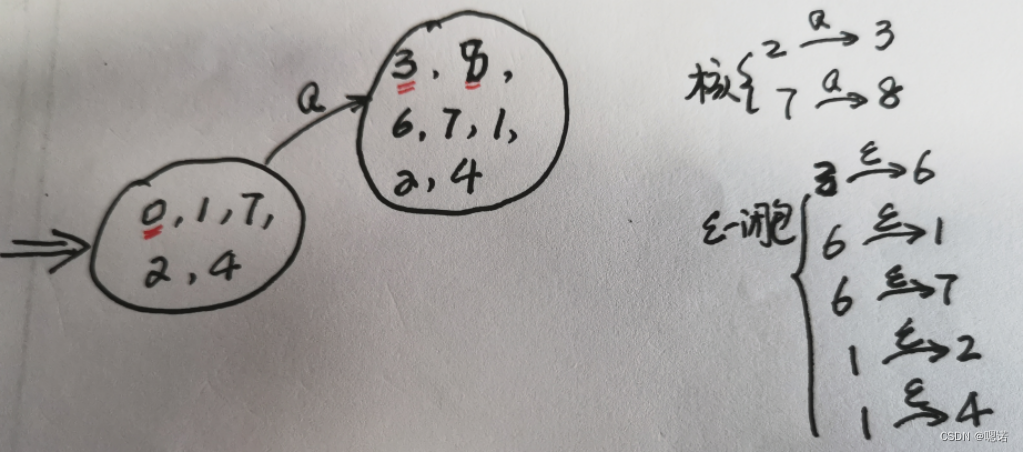
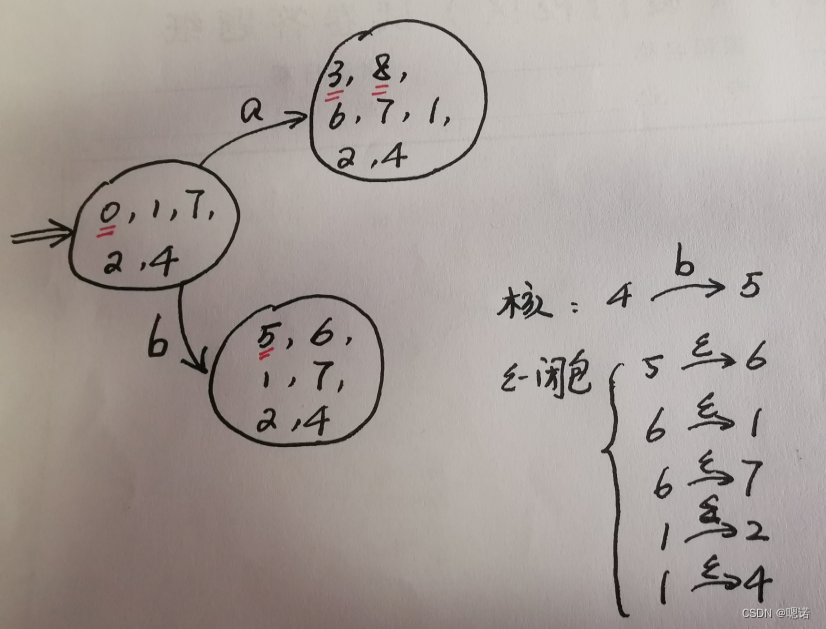
(3)使用子集构造法将NFA转换为DFA (关键在求闭包)
状态转移矩阵例题
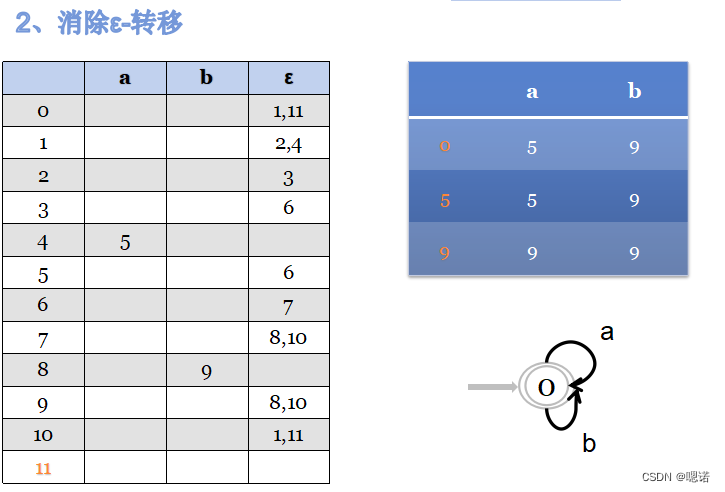
(a|b)*b
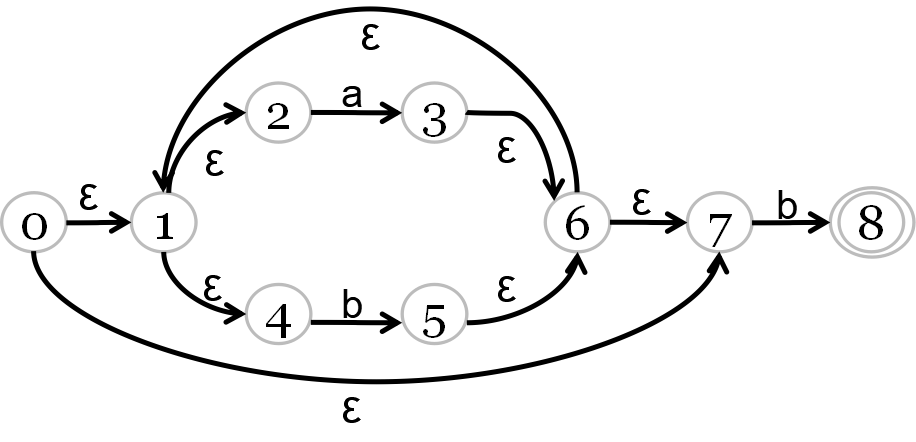
1、转换成状态转移矩阵

2.消除空转移
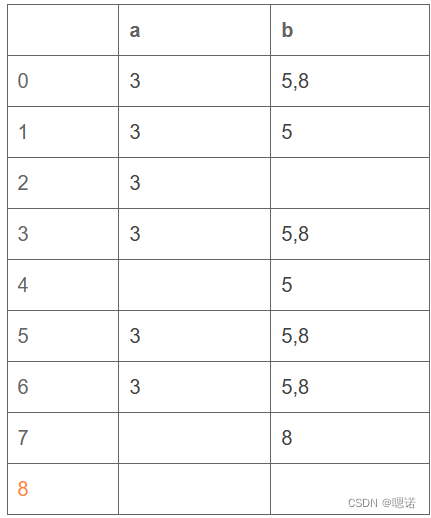
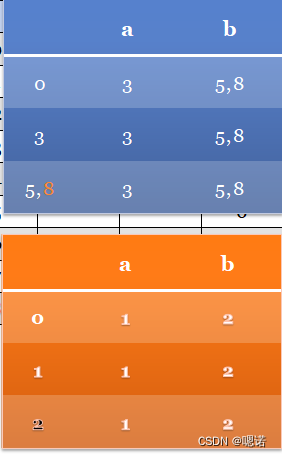
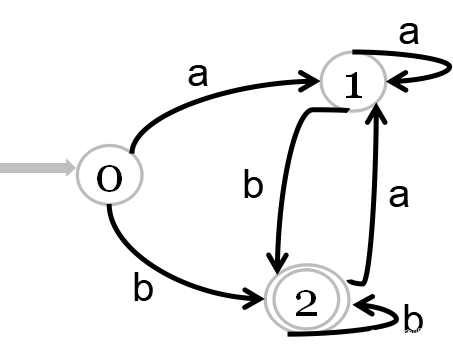
综合例题1
r=(0|1)*011(0|1)*
1、正规式→NFA
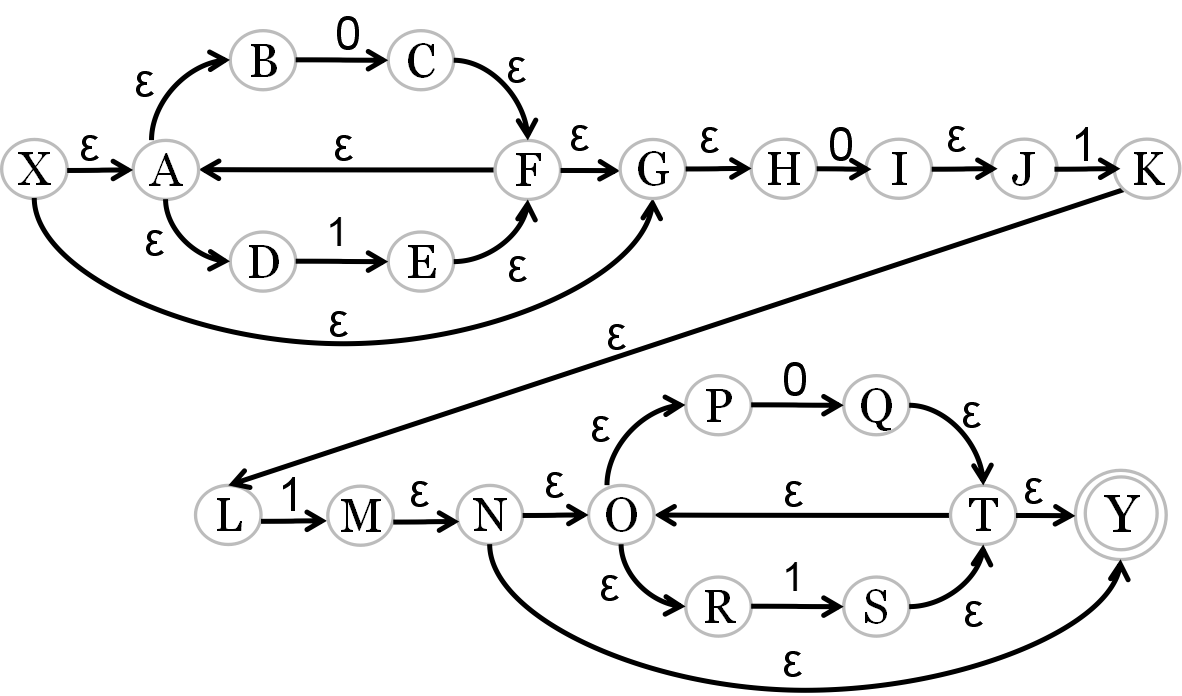
2、NFA→DFA(状态转移图)
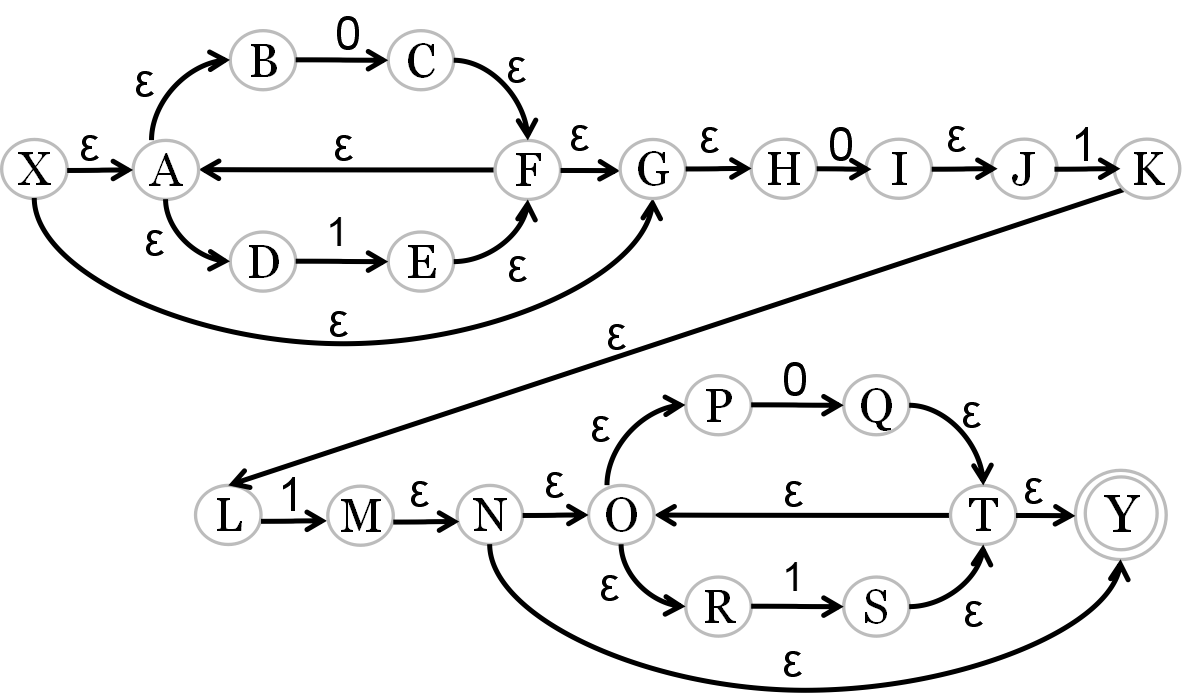


综合例题2:
((ε|a)b*)*
1、正规式→NFA
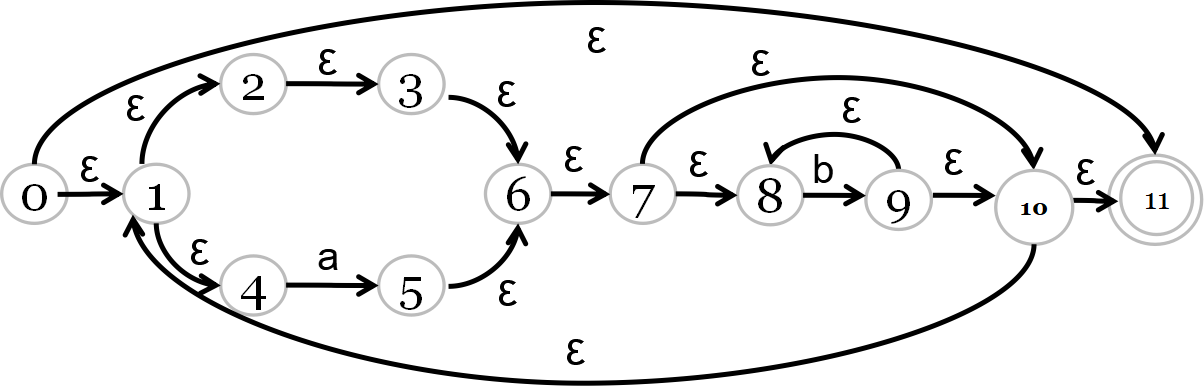
2、NFA→DFA(状态转移图)

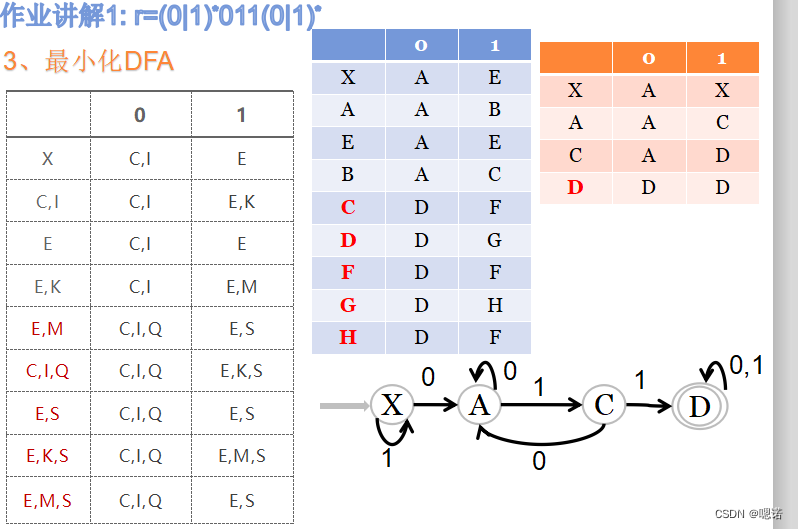
八、最小化DFA
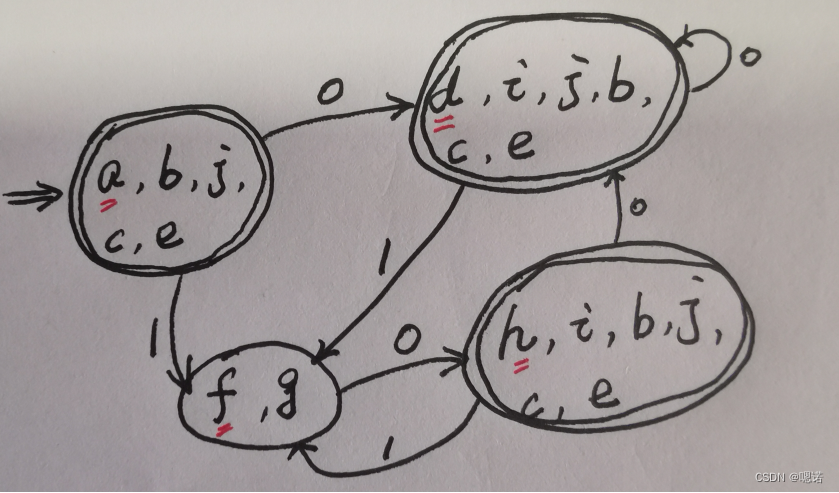
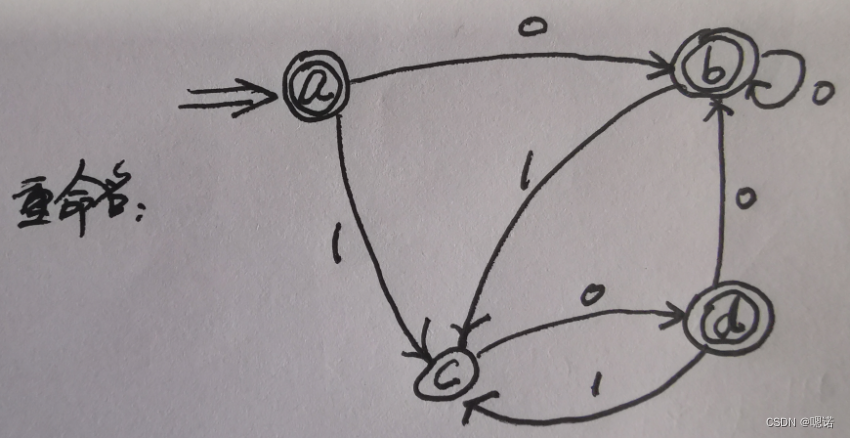
它们接受相同的正规集,说明两个DFA是等价的,但是有可能他们的状态数不同。一般来说,对于若干个等价的DFA,总是希望由状态数最少的DFA构造词法分析器。将一个DFA等价变换为另一个状态数最少的DFA的过程被称为最小化DFA,相应DFA称为最小DFA。
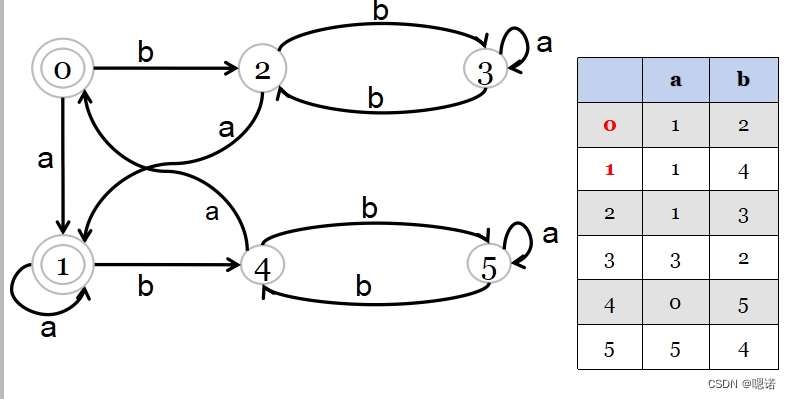
练习判断正规式(a|b)*b和正规式((a|b)*|aa)*等价
方法:将两个正规式各自处理至最小DFA,然后比较是否一致。
九、消除左递归
什么时候需要消除左递归
在进行自上而下的分析(比如LL(1)分析时,构造预测分析器也是LL(1)分析)需要消除左递归,因为自上而下的分析方法不能用于左递归文法。任何二义文法绝不是LR文法。
直接左递归:将A ------> Aα | β 转换为
A ------> β A'
A' ------> α A'
间接左递归:
先将其变为立即左递归(前面的式子代入后面式子)
然后按照消除直接左递归的规则进行转换即可
消除直接左递归:
将以下文法消除左递归:
E -> E+T | T
T -> T*F | F
F -> (E) | i
消除左递归:
E→TE'
E'→+TE'|ε
T→FT'
T'→*FT'|ε
F→(E)|i
消除间接左递归1
1)B→aBc
2)B→Bbc
3)B→d
先将其变为立即左递归,可化简为:B→aBc | Bbc | d
然后按照消除直接左递归的规则进行转换即可
1)B→aBcB' |dB'
2)B'→bcB' |ε
消除间接左递归2:

十、求first集合
FIRST( α )表示由α推导出的串的首个终结符或空字符组成的集合。
规则
求文法符号X的FIRST( X ) ,直到没有终结符或空字符可以加入。
① 如果X属于终结符VT,则FIRST(X) = { X } 。
② 如果X属于非终结符VN,且有产生式形如X → a...,则FIRST( X ) = { a }。
③ 如果X属于非终结符VN,且有产生式形如X → ABCdEF...(A、B、C均属于非终结符且包含 ε,d为终结符),需要把d、FIRST( A )、FIRST( B )、FIRST( C )加入到FIRST( X)中。
④ 如果X经过一步或多步推导出空字符ε,将ε加入FIRST( X )。
我们主要使用的是规则2 和规则3,理论上每次First集产生变化就要重新查看一遍所有式子,实际做题时可以按照变化一次重新求一次
例题1:
G[E]:
E→TE′
E′→+TE′∣ε
T→FT′
T′→∗FT′∣ε
F→(E)∣i
1.使用规则2,即产生式右边的第一个字母如果是终结符或者单独的ε即可写入first集合,遍历第一遍可得
First(E) = { }
First(E′ ) = {+,ε}
First(T) = { }
First(T′ ) = { *,ε }
First(F) = { (,i}
2.使用规则3进行第一次遍历,即产生式右边的第一个字母使用对应的first集合
First(E) = { }//E→TE′可知first(T)要写进first(E)但是此时T为空所以不写
First(E′ ) = {+,ε }
First(T) = { (,i }
First(T′ ) = { *,ε }
First(F) = { (,i }
3.使用规则3进行下一次遍历,即产生式右边的第一个字母使用对应的first集合,直到不再发生变化
First(E) = {(,i }
First(E′ ) = {+,ε}
First(T) = { (,i }
First(T′ ) = { *,ε }
First(F) = { (,i }
4.重点观察产生式右边从第一个字母开始的连续出现的非终结符,观察这几个大写字母的first集是否出现ε(详细看规则表述)
本题目只有下面两个式子复合要求
E→TE′
T→FT′
因为First(T) = { (,i },First(F) = { (,i }均不含ε,所以本题完成
例题2:
A→BCc | gDB
B→bCDE | ε
C→DaB | ca
D→dD | ε
E→gAf | c
1.使用规则2,即产生式右边的第一个字母如果是终结符或者单独的ε即可写入first集合,遍历第一遍可得
First(A) = { g}
First(B ) = {b,ε}
First(C) = {c }
First(D) = { d,ε }
First(E) = { g,c}
2.使用规则3进行第一次遍历,即产生式右边的第一个字母使用对应的first集合
First(A) = {g,b,ε }
First(B ) = {b,ε}
First(C) = {c ,d,ε}
First(D) = { d,ε }
First(E) = { g,c}
3.使用规则3进行下一次遍历,即产生式右边的第一个字母使用对应的first集合,直到不再发生变化,(发现第二轮就不发生变化了)
First(A) = {g,b,ε }
First(B ) = {b,ε}
First(C) = {c ,d,ε}
First(D) = { d,ε }
First(E) = { g,c}
4.重点观察产生式右边从第一个字母开始的连续出现的非终结符,观察这几个大写字母的first集是否出现ε(详细看规则表述)
本题目只有下面两个式子复合要求
A→BCc
C→DaB
第一个式子:因为First(B ) = {b,ε},所以first(A)加上first(C),First(A) = {g,b,ε,c,d },而First(C) = {c ,d,ε}含有ε,所以C后面的c也要加入first(A),First(A) = {g,b,ε,c,d }
第二个式子:因为First(D) = { d,ε },所以First(C) = {c ,d,ε,a}
从第2步开始重复
First(A)= {g,b,ε,c,d,a }
First(B ) = {b,ε}
First(C) = {c ,d,ε,a}
First(D) = { d,ε }
First(E) = { g,c}
另一种写法:
解:
FIRST( A ) = FIRST( BCc ) ∪ FIRST( gDB )
=FIRST( B )∪FIRST( C )∪{ c }∪{ g }
由规则③规则②可知
FIRST( A ) =FIRST( B )∪FIRST( D )∪{ a }∪{ c }∪{ c }∪{ g }
={ b,ε }∪{ d,ε }∪{ a }∪{ c }∪{ g }
={ a,b,c,d,g ,ε }
FIRST( B ) = { b,ε }
FIRST( C ) = FIRST( D )∪{ a }∪{ c }= { a,c,d,ε }
FIRST( D ) = { d,ε }
FIRST( E ) = { g,c }
对于A来说:有两种选择 BCc 与 gDB,BCc用规则③,gDB用规则②。
对于B来说:有两种选择 bCDE 与 ε,均用规则②。
对于C来说:有两种选择 DaB 与 ca,由于D存在空字符,所以 DaB用规则③,ca用规则②。
对于D来说:有两种选择dD 与 ε ,分别用规则②与规则④。
对于E来说:有两种选择gAf 与 c ,均用规则②。
例题3:
设有文法G[S]:
S→aBS | bAS | ε
A→bAA | a
B→aBB | b
解:
FIRST( S ) = FIRST( aBS )∪FIRST( bAS )∪{ ε }={ a,b,ε }
FIRST( A ) = { a,b }
FIRST( B ) = { a,b }
对于S来说:有三种选择 aBS与bAS、ε,分别用②与规则④。
对于A来说:有两种选择bAA与 a,均用规则②。
对于B来说:有两种选择aBB与 b,均用规则②。
写在最后:其实我喜欢用目测法,就从倒数第一个产生式开始,看见小写字母和单独的ε直接写进first,如果是大写字母,就找它的first,然后看它的 first有没有空,有空就往下个字母看
十一、follow集合
Follow集合求取的是非终结符的后继符号集合,不能出现空字符ε 。以X表示一个非终结符,FOLLOW( X )表示当X通过规约出现时,接下来的输入可能是哪些终结符。
规则求非终结符X的FOLLOW( X ) ,直到没有终结符可以加入。
① 如果X是开始符号,则将#加入到FOLLOW(X)中 。
② 如果存在一个产生式S->αXβ,那么将集合FIRST(β)中除ε外的所有元素加入到FOLLOW(X)当中。
③如果存在一个产生式 S->αX , 或者S->αXβ且FIRST(β)中包含ε , 那么将集合FOLLOW(S)中的所有元素加入到集合FOLLOW(X)中。
例题1:
G[E]:
E→TE′
E′→+TE′∣ε
T→FT′
T′→∗FT′∣ε
F→(E)∣i
first集合如下:
First(E) = {(,i }
First(E′ ) = {+,ε}
First(T) = { (,i }
First(T′ ) = { *,ε }
First(F) = { (,i }
1.将#加入开始符号E的follow集合
Follow(E) = { # }
Follow(E′) = { }
Follow(T) = { }
Follow(T′) = { }
Follow(F) = { }
2.找到产生式右边的每一个非终结符还有它们后面的字符,并将后面的first集合去ε后加入follow集,有空还有看下一个字符
Follow(E) = { # ,)}//F→(E)
Follow(E′) = { }
Follow(T) = { +}//E→TE′且E′虽有空但后面无紧跟字母
Follow(T′) = { }
Follow(F) = {* }//T′→∗FT′且T ′虽有空但后面无紧跟字母
3.找到产生式右边的最后一个字母,如果是终结符则不用管,如果是非终结符,则将该产生式左边的follow集加入,若该字母可取空,则还要看上一个字符是否为非终结符,则将该产生式左边的follow集加入
Follow(E) = { # ,)}
Follow(E′) = { ),#}//E→TE′
Follow(T) = { +,#,)}//E→TE′
Follow(T′) = {+,# ,)}//T→FT′
Follow(F) = {*,+,#,) }
4.重复3直至follow集合不再发生变化(本题在刚刚第3 步已经不再变化了)
例题2:
设有文法G[A]:
A→BCc | gDB
B→bCDE | ε
C→DaB | ca
D→dD | ε
E→gAf | c
First集合如下:
First(A)= {g,b,ε,c,d,a }
First(B ) = {b,ε}
First(C) = {c ,d,ε,a}
First(D) = { d,ε }
First(E) = { g,c}
第一种写法:
FOLLOW( A ) ={ f ,# }
FOLLOW( B ) = FIRST( C )∪FOLLOW( A )∪FOLLOW( C )
={ a,c,d }∪{ f ,#}∪{ c,d,g,# }
={ a,c,d,f,g,# }
FOLLOW( C ) = { c }∪FIRST( D )∪FIRST( E )
={ c }∪{ d }∪{ g,c }
={ c,d,g }
FOLLOW( D ) = FIRST( B )∪FOLLOW(A )∪FIRST( E )∪{ a }
={ b } ∪{ g,c }∪{ f ,# }∪{ a }
={ a,b,c,g,f,# }
FOLLOW( E ) = FOLLOW( B )
={ a,c,d,f,g,# }
第二种写法:
FOLLOW( A ) ={#}
FOLLOW( B ) = {}
FOLLOW( C ) ={}
FOLLOW( D ) ={}
FOLLOW( E ) = {}
FOLLOW( A ) ={#,f}
FOLLOW( B ) = {c ,d,a}
FOLLOW( C ) ={c,d,g}
FOLLOW( D ) ={b,g,c,a}
FOLLOW( E ) = {}
FOLLOW( A ) ={#,f}
FOLLOW( B ) = {c ,d,a,f,#,g}
FOLLOW( C ) ={c,d,g}
FOLLOW( D ) ={b,g,c,a,#,f}
FOLLOW( E ) = {c ,d,a,f,#}
4,重复找follow
FOLLOW( A ) ={#,f}
FOLLOW( B ) = {c ,d,a,f,#,g}
FOLLOW( C ) ={c,d,g}
FOLLOW( D ) ={b,g,c,a,#,f}
FOLLOW( E ) = {c ,d,a,f,#,g}
例题3:
设有文法G[S]:
S→aBS | bAS | ε
A→bAA | a
B→aBB | b
first集合如下:
FIRST( S ) = { a,b,ε }
FIRST( A ) = { a,b }
FIRST( B ) = { a,b }
FOLLOW( S ) ={#}
FOLLOW( A) ={}
FOLLOW( B )={}
FOLLOW( S ) ={#}
FOLLOW( A) ={a,b}
FOLLOW( B )={a,b}
FOLLOW( S ) ={#}
FOLLOW( A) ={a,b,#}
FOLLOW( B )={a,b,#}
十二、求selcet集
作用:用SELECT集判断是否为LL(1)文法的例题:
步骤:
对于产生式A →α
1)若 α≠*> ε,则SELECT(A →α)= FIRST(α)
2)若 α=*> ε,则SELECT(A →α)= FIRST(α)∪FOLLOW(A)
自我理解:直接看产生式的右边的第一个字母(不管是否是终结符),SELECT集直接取FIRST(产生式右边),如果FIRST集合里有ε,保留ε且在SELECT集里添上FOLLOW(产生式左边)
例题:
G(E):
①E → TE'
②E' → +TE'
③E' →ε
④T → F T'
⑤T' → *F T'
⑥T' →ε
⑦F → (E)
⑧F → id
实现准备好:在这个文法中能推出ε的产生式的左部为:{ E',T' }
FIRST(E)= {(,id }
FIRST(E`)= {+,ε }
FIRST(T)={(,id }
FIRST(T')={*,ε }
FIRST(F)={(,id }
Follow(E)= { ),$ }
Follow(E)'= { ),$ }
Follow(T)={ +,),$ }
Follow(T')={ +,),$ }
Follow(F)={ *,+,),$ }
下面,我们来计算这个文法的SELECT集。
第①条产生式:①E → TE'
因为FIRST(T)中没有ε ,所以第一条产生式的SELECT计算就结束了。E → TE' { (,id }
第②条产生式:E' → +TE'
产生式的右部首符号为+,是一个终结符,我们可以得到E' → +TE' { + }
第③条产生式:E' →ε ,我们发现该产生式推出一个空,我们可以得到E' →ε { ε,),$ }
第④条产生式:T → F T',T → F T' { (,id }
第⑤条产生式:T' → *F T' ,与第②条产生式同理,T' → *F T' { * }
第⑥条产生式:T' →ε ,与第③条产生式同理,T' →ε { ε,+,),$ }
第⑦条产生式:F → (E),F → (E) { ( }
第⑧条产生式也同理:F → id { id }
∴该文法的SELECT集为:
① SELECT(E → TE' )= { (,id }
② SELECT(E' → +TE' )= { + }
③ SELECT(E' →ε )= { ε,),$ }
④ SELECT( T → F T' )= { (,id }
⑤ SELECT(T' → *F T' )= { * }
⑥ SELECT(T' →ε )= { ε,+,),$ }
⑦ SELECT(F → (E))= { ( }
⑧ SELECT(F → id )={ id }
十三、LL(1)文法
满足条件:
① 文法无左递归。
②如果A存在多个选择ai,那么任意两个不同的选择ai和aj,需满足FIRST( ai )∩FIRST( aj )= ∅ ,保证不会回溯。
③如果ε 属于A 的开始符号集合,需满足FIRST( A )∩FOLLOW( A ) = ∅ 保证只有一个选择存在。
另一种判断是否为LL(1)的方法:
求出每个表达式的SELECT集合,将产生式左端相同的表达式归为一组,若一组之间的SELECT集合之间交集为空,则该文法就是LL(1)文法,否则就不是。
十四、构造预测分析表
判断是LL(1)文法后,就可以构造预测分析表了
设有文法G[A]:
A→aB|ε
B→Ab|d
(1)判断是否为LL(1)文法
(2)构造分析表
FIRST(A)={a,ε},FIRST(B)={d,b,a}
FOLLOW(A)={#,b},FOLLOW(B)={#,b}
SELECT(A→aB)={a}
SELECT(A→ε)={#,b}
SELECT(B→Ab)={a,b}
SELECT(B→d)={d}
观察可知,同组SELECT集合交集为空,所以该文法是LL(1)文法
|---|------|------|-----|-----|
| | a | b | d | # |
| A | A→aB | A→ε | | A→ε |
| B | B→Ab | B→Ab | B→d | |
方法很简单:
先看终结符出现在哪个产生式的SELECT集中,就把那个产生式填到与产生式左部一样的那一行。比如对于a,在SELECT(A→aB)和SELECT(B→Ab)中出现,那就把对应产生式填进去
十五、构造文法的LR(0)
解释:右部某位置标有圆点的产生式称为相应文法的一个LR(0)项目(简称为项目),
- 产生式A→ε 只生成一个项目A→ ·
- 移进项目: 形如 A -> α• aβ,对应移进状态,圆点后面是终结符。
待约项目: 形如 A -> α • Bβ,对应待约状态,圆点后面是非终结符
归约项目: 形如 A -> α •,句柄已形成(圆点在最后面),可以归约。
接受项目: 形如 S' -> S •(S是初始符号,S'是增广之后的初始符号)。
初始项目: 形如 S' -> • SS是初始符号,S'是增广之后的初始符号)。
其中a∈VT , α,β∈(VN∪VT)*, A,B∈VT
后继项目: 表示同属于一个产生式的项目,但是圆点的位置仅相差一个文法符号,则称后者为前者的后继项目。举例说明:S-->bBB则可以推导出4个项目
例题:
给定文法G[E]:
(1) E -> E+T
(2) E -> T
(3) T -> ( E )
(4) T -> d
构造LR(0)
① G[E]的拓广文法,得到G' [E']:
(0) E' -> E
(1) E -> E+T
(2) E -> T
(3) T -> ( E )
(4) T -> d
②构造G'[E'] 的 LR(0)
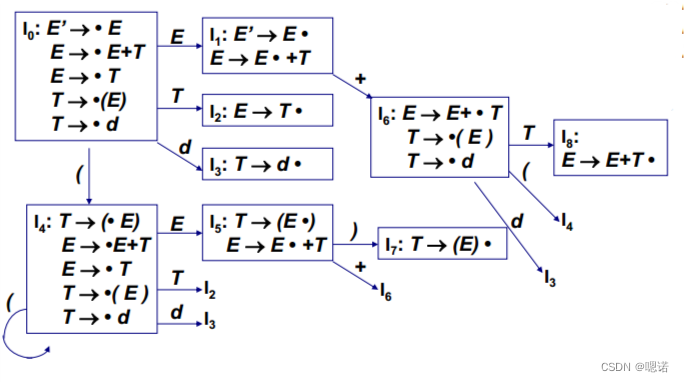
上面的LR(0)项目簇规范族:I0={E'->.E,E->.E+T,E->.T,T->.(E),T->.d};I1={E'->E. ,E->E.+Td}........I8={E->E+T.}
接下来找含有规约的项目,判断是否存在移进(小黑点在终结符的前面)/规约(小黑点在最后面)冲突,看I1就是典型的冲突(如果写到LR(0)分析表上,就会出现一个格子两个不同的动作),所以该文法不是LR(0)文法
如果LR(0)分析表中没有语法分析动作冲突 ,那么给定的文法就称为**LR(0)文法,**不是所有CFG【上下文无关文法】都能用LR(0)方法进行分析,也就是说,CFG不总是LR(0)文法
例题2:
**技巧:**当下一个读入的符号是非终结符的时候,我们填写GOTO表,只需要填写I将要取到的那个项目集的数字(I旁边的数字)即可。当下一个读入字符是终结符的时候,我们就需要判断是移进(小黑点后面是终结符)还是归约(小黑点在最后面),规约的话要判断是不是ACC
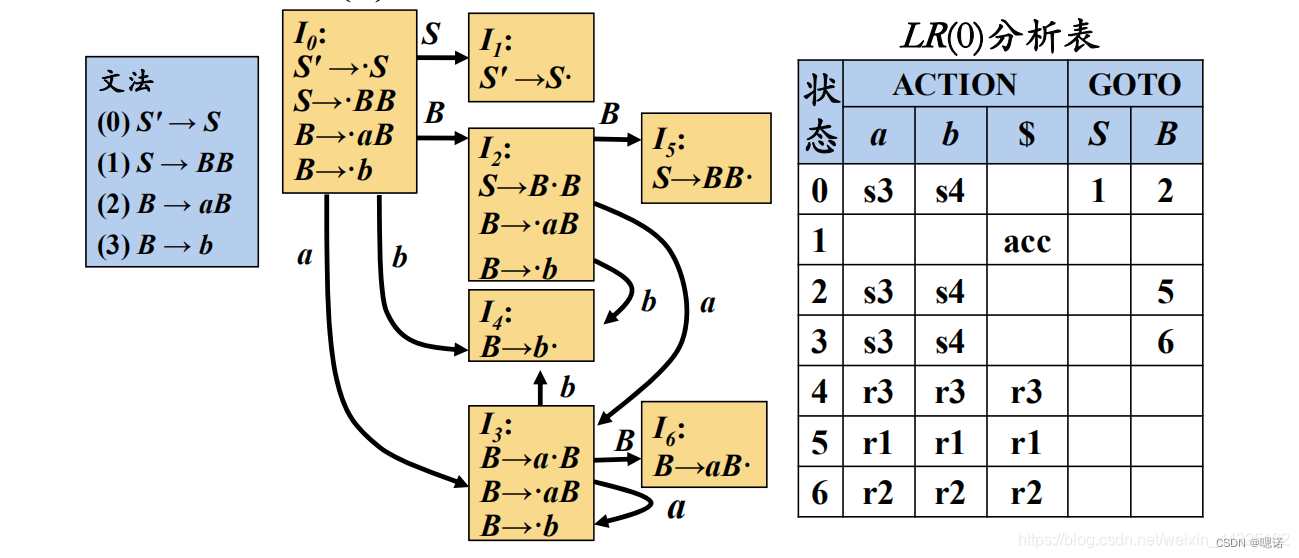
十六、 SLR
上一题型简要的说明了一下LR(0)分析在构建分析表时候会发生的一些冲突。为了解决LR(0)分析产生冲突,故学习SLR(1),意思是在解决LR(0)冲突的时候,我们需要向后多看一个字符(又因为k=1的时候,可以省略不写,所以可以简写为SLR)。如果给定文法的SLR分析表中不存在有冲突的动作,那么该文法称为SLR文法

对于一个LR(0)分析存在冲突,就多往后面多看一个字符。具体解题步骤是,对产生冲突的产生式的左边那个非终结符求FOLLOW集,然后判断下一个输入字符是否在其式子左边那个字符中的FOLLOW集中,如果在,对于输入该字符就采用该项目对应的操作,要是都不在就报错。
当我们采用SLR分析时发现,SLR依然是可能存在语法冲突的,因为原因:SLR只是简单地考察下一个输入符号b是否属于与归约项目A→α相关联的FOLLOW(A),但是b∈FOLLOW(A)只是归约α的一个必要条件,而非充分条件,即如果输入下一个字符是b,我们采用了归约操作,那么就一定可以说明b属于A的FOLLOW集,但是我们不能说:如果b属于A的FOLLOW集,那么就一定可以对A采用归约操作。
为解决冲突那么就可以引入了LR(1)分析。
十七、LR(1)文法
搜索符的两种传播方式:
1.项目[A->α.Bβ,a],当β能导出空串时,该项目的
搜索符a传播到项目[B->...,a],称为纵向传播
2.项目[A->α.B β,a],搜索符a传播到项目[A->αB .β,a]
称为横向传播
步骤:1、拓广文法并编号
2、项目集规范族(带向前搜索符)
3、LR(1)分析表
例题1:
G[S]:
S->BB
B->bB|a
解答如下
1、拓广文法并编号
S'->S(0)
S->BB(1)
B->bB(2)
B->a(3)
2、项目集规范族(带向前搜索符)
3、LR(1)分析表
例题2
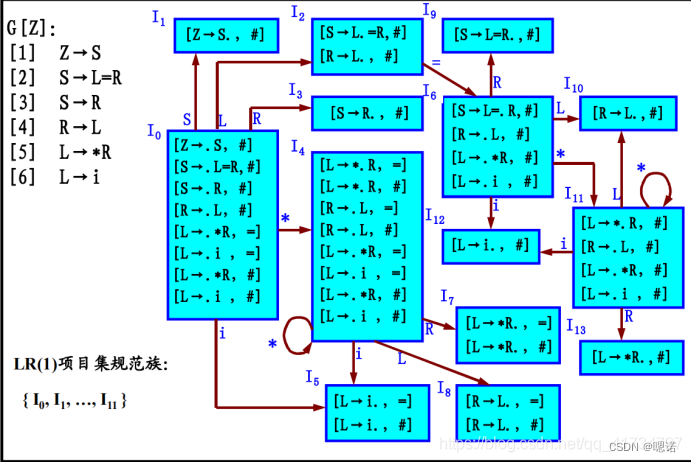
十八、写出表达式的四元式
三条规则:
1.格式:(运算符,运算对象,运算对象,临时变量)
2.先处理优先级高的一部分,然后左遍历
3.每一次运算结果用一个临时变量储存,以便后续使用
例题1:a+b*(c/d+g)
(/,c,d,t1)
(+,t1,g,t2)
(*,b,t2,t3)
(+,a,t3,t4)
例题2:a+b*(c-d)+f/(c-d)^n
(-,c,d,t1)
(*,b,t1,t2)
(+,a,t2,t3)
(-,c,d,t4)
(^,t4,n,t5)
(/,f,t5,t6)
(+,t3,t6,t7)
十九、文法
属性文法

综合属性

继承属性