2023年第十四届蓝桥杯JavaB组省赛真题及全部解析（上）

[一、试题 A：阶乘求和（填空）](#一、试题 A：阶乘求和（填空）)

[二、试题 B：幸运数字（填空）](#二、试题 B：幸运数字（填空）)

[三、试题 C：数组分割](#三、试题 C：数组分割)

[四、试题 D：矩阵总面积](#四、试题 D：矩阵总面积)

[五、试题 E：蜗牛](#五、试题 E：蜗牛)

[六、试题 F：合并区域](#六、试题 F：合并区域)

前言：

这一篇是我蓝桥系列的第一篇，当然现在第十五届蓝桥杯已经打完了，作者也有参加，运气比较好，拿了个国二，虽然没有达到自己的预期，但也是完成学校的任务，作者是福建省的（弱省），省一我觉得还是挺简单的，随便 ac 两题，打打暴力就省一了，排名还很靠前。蓝桥杯的含金量肯定是不如 ICPC（ACM）和 CCPC （中国的ACM），这个我是深有体会，因为我有参加 CCPC 福建省邀请赛（福州大学），暴零了（一题都没有做出来），直接去旅游了😭😭😭。只能说那种级别的比赛真不是一般人能打的。接下来我会分享我备赛蓝桥杯过程刷的真题和解析，方便和我一样第一次参加蓝桥杯的小白备赛。由于题目比较多，后面几题的题解比较长，只能分成两篇来发，如果有需要的话可以点开下部分，讲解了第 7 到第 10 题。

题目来自：蓝桥杯官网

一、试题 A：阶乘求和（填空）

• 题目分析：

在这里先提醒大家一下，填空题做不出来很正常，我当时填空题第一题也没做出来（就是有点影响心态）。看到这个题，202320232023 这个数的阶乘是不能开 BigInteger 的（这个数非常大），会爆掉的，且这么大的数，在比赛时间内都不一定能跑完。所以我们只能找规律，比赛的时候找不出来的话，可以先把 1 到 50 的结果打印出来。说不定就能找到规律，直接使用计算器算（可以使用计算器）。下面就是就是第 i 阶乘的后 9 位，要取模不然 long 存不下，比赛发现这个规律就可以填了（要珍惜时间）。

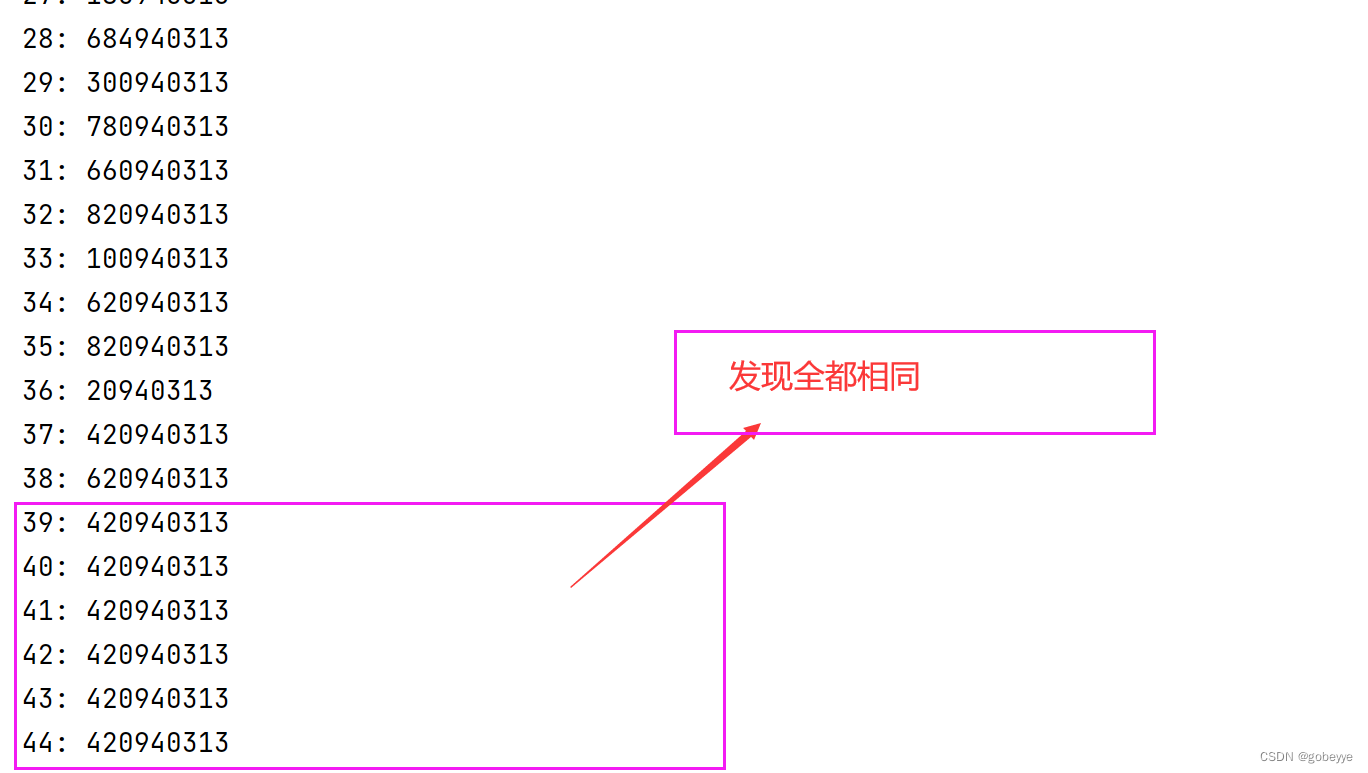
• 解题思路：

我们可以观察到当阶乘的底数大于等于 5 时，阶乘结果的末尾将开始出现 0。这是因为阶乘结果中含有至少两个因子 2 和 5，而 2 和 5 相乘正好为 10（结尾就会出现 0 ）。

在一个正整数阶乘的时候，因子 2 的个数一定不小于因子 5 的个数，因此我们只需要考虑因子 5 的个数即可。当因子 5 的个数大于等于 9 时，这个阶乘的后面 9 位就都为 0 了，因此这个阶乘后面就不用再考虑了。

我们可以看到在正整数中因子为 5 出现在 5，10，15，20，25（可以算两个），30，35，40，45.....而我们只要前面 9 个即可，也就是 40 之前。当阶乘数大于等于 40 时，结尾 9 位数都是0.

因此本题其实只要计算前 40 个阶乘之和。从 40！开始以后都不会影响到最终的结果。

注意：在运算的过程中要取模防止溢出（MOD取 1e9 即可，正好是后面 9 位）。

• 代码编写：

java 复制代码

public class Main {
    public static void main(String[] args) {
        int MOD = (int) 1e9;
        long sum = 0;//保存和
        long mul = 1;
        for (int i = 1; i < 40; i++) {//阶乘的求法
            mul = (mul * i) % MOD;
            sum = (sum + mul) % MOD;
        }
        System.out.println(sum);
    }
}

• 运行结果：

二、试题 B：幸运数字（填空）

• 题目分析：

不要被题目吓到了，读过题目就会发现这是一道签到题，2023 也不会很大。

• 解题思路：

按照题目的意思模拟即可。

• 代码编写：

binary是求出 n 在 base 进制下的各位数和。

java 复制代码

public class Main {
    public static void main(String[] args) {
        int count = 0;
        for(long i = 1;;i++){
            if(i % binary(i,2) == 0 && i % binary(i,8) ==0 && i % binary(i,10) == 0
            && i % binary(i,16) == 0){//根据题意模拟
                count++;
            }
            if(count == 2023){
                System.out.println(i);
                return;
            }
        }
    }
    public static int binary(long n,int base){//求出 n 在 base 进制下的各位数和
        int sum = 0;
        while(n > 0){
            sum += n % base;
            n /= base;
        }
        return sum;
    }
}

• 运行结果：

三、试题 C：数组分割

由于题目加上输入各式和输出格式比较长，需要的友友自行去官方那里看就行。

• 题目分析：

题目简单可以理解为：将一个数组分为两个偶数数组（0 也是偶数）。根据数学性质，两个偶数相加的和一定也为偶数，因此如果给出的数组总和不是偶数的话直接打印 0 即可。直接讨论两组数组的所有情况非常麻烦。考虑到总和已经为偶数，因此我们只需找出其中 1 个数组的总和为偶数（另一个数组一定也是偶数）的所有情况，就是我们的最终答案。最终这个问题就转化成了类似 01 背包问题，从 1 到 n 的数中选，总和为偶数的有多少种情况。

• 解题思路：

这是一道动态规划题，我们要先定义出状态表示。

1. 状态表示：

f[i]：表示在前 i 个数中选，总和为偶数的所有情况个数。

g[i]：表示在前 i 个数中选，总和为奇数的所有情况个数。

2. 状态转移方程：

我们以最后一个位置的元素 a[i] 来研究。

（1）当 a[i] 为偶数时：

f[i]：可以从前 i - 1 个数的所有，和为偶数的方案中（选或者选 a[i]）转移过来。

g[i]：可以从前 i - 1 个数的所有，和为奇数的方案中（选或者不选 a[i]）转移过来。

故在 a[i] 为偶数的状态转移方程为：

f[i] = 2 * f[i - 1];

g[i] = 2 * g[i - 1];

（2）当 a[i] 为奇数时：

f[i]：可以分别从前 i - 1 个数的所有，和为偶数的方案中（不选 a[i]）、前 i - 1 个数的所有，和为奇数的方案中（选 a[i]）转移过来。

g[i]：可以分别从前 i - 1 个数的所有，和为偶数的方案中（选 a[i]）、前 i - 1 个数的所有，和为奇数的方案中（不选 a[i]）转移过来。

f[i] = f[i - 1] + g[i - 1];

g[i] = f[i - 1] + g[i - 1];

3. 初始化

因为数组为空时也算一个偶数方案。所以设 f[0] = 1即可。

• 代码编写：

java 复制代码

import java.util.*;
public class Main {
    public static void main(String[] args) {
        Scanner in = new Scanner(System.in);
        int MOD = (int) 1e9 + 7;
        //dp
        int T = in.nextInt();
        while (T > 0) {
            int n = in.nextInt();
            int[] nums = new int[n + 1];
            long sum = 0;
            for (int i = 1; i <= n; i++) {
                nums[i] = in.nextInt();
                sum += nums[i];
            }
            if (sum % 2 == 1) {//特判
                System.out.println(0);
            }else {
                //1.创建 dp 表
                int[] f = new int[n + 1];
                int[] g = new int[n + 1];
                f[0] = 1;
                //2.初始化
                //3.填表
                for (int i = 1; i <= n; i++) {
                    if (nums[i] % 2 == 0) {
                        //偶数情况
                        f[i] = (2 * f[i - 1]) % MOD;
                        g[i] = (2 * g[i - 1]) % MOD;
                    } else {
                        //奇数情况
                        f[i] = (f[i - 1] + g[i - 1]) % MOD;
                        g[i] = (f[i - 1] + g[i - 1]) % MOD;//sb了g + g，抄错了
                    }
                }
                //4.返回值
                System.out.println(f[n]);
            }
            T--;
        }
    }
}

• 时间复杂度：

O（T * N）。 T 为测试数据的组数，n 为每组数据个数。能过。

• 运行结果：

四、试题 D：矩阵总面积

• 题目分析：

本题是考计算几何的知识，本题的难点在于如何计算出矩阵重合地方的面积，这一块考的较少，如果知道重合地方的面积怎么算的话，这题就是送分的，如果不知道的话，就模拟打打暴力整点分。

• 解题思路：

先算出全部面积（y2 - y1）* (x2 - x1)，另一个同理。

计算重叠部分的面积：

x轴上的重叠长度：k = max(0,min(x2,x4) - max(x1,x3));

y轴上的重叠长度：k = max(0,min(y2,y4) - max(y1,y3));

之所以和 0 取较大的数，是为了避免两个矩形没有重叠的地方，计算出来的结果会是负数，为了避免这种情况，我们使用 max 函数，当两个矩形没有重叠时，重叠长度为 0 。（这个公式我是看别人的，怎么来的我也不知道）

暴力：

可以创建一个二维数组，把两个矩形填上，最后遍历矩形，有多少个格子被填充，面积就是多少。

时间复杂度O（n ^ 2）。超时，但是能骗到不少分数。代码不难我就不实现了。

• 代码编写：

java 复制代码

import java.util.*;
public class Main {
    public static void main(String[] args) {
        Scanner in = new Scanner(System.in);
        //读入数据
        long x1 = in.nextLong(),y1 = in.nextLong(),x2 = in.nextLong(),y2 = in.nextLong();
        long x3 = in.nextLong(),y3 = in.nextLong(),x4 = in.nextLong(),y4 = in.nextLong();
        long sum = ((y4 - y3) * (x4 - x3)) + ((y2 - y1) * (x2 - x1));//全部面积
        long sub = Math.max(0,((Math.min(y4,y2) - Math.max(y1,y3)) * (Math.min(x4,x2) - Math.max(x1,x3))));//重复面积
        sum -= sub;
        System.out.println(sum);
    }
}

• 时间复杂度：

O（1），肯定能过。

• 运行结果：

五、试题 E：蜗牛

• 题目分析：

根据题意求最少时间，且有走地面和爬杆坐传送门两种方式，发现存在某种递推关系，故我们可以尝试使用动态规划解决。

• 解题思路：

1. 状态表示：

f[i]：表示到达第 i 根竹竿的底部的最小时间。

g[i]：表示到达第 i 根竹竿的传送门（a [i] ,不是 b [i - 1]）的最小时间。

2. 状态转移方程：

h[i][2] 使用 h[i][0] 来表示 a[i]，使用 h[i][1] 来表示 b[i + 1]。

我们以最后一个位置来分析：

（1）对于 f[i] 有两种情况：

• 可以从前一根杆的底部走到当前杆的底部：f[i] = f[i - 1] + a[i] - a[i - 1];

• 可以从前一根杆的传送门传送到当前杆，再爬下来：g[i] = g[i - 1] + h[i - 1][1] / 1.3;

注意：因为这里 f[i - 1] 已经表示到达第i - 1根杆的最小时间，所以就不用考虑存在从 i - 1根杆的传送门爬到底部，再走到当前杆底部的这种情况（因为肯定没有 f[i] = f[i - 1] + a[i] - a[i - 1] 快）。

（2）对于 g[i] 也有两种情况：

• 可以从前一根杆的底部爬到当前杆的底部，再爬到传送门：g[i] = f[i - 1] + a[i] - a[i - 1] + h[i][0] / 1.3;

• 可以从前一根杆的传送门传送到当前杆，再爬到当前杆的 a[i]（传送过来是在 b[i - 1]）。注意：这里要分情况讨论，因为不确定是向上爬还是向下爬。g[i] = g[i - 1] + (h[i - 1][1] >= h[i][0]) ? )h[i - 1][1] - h[i][0]) / 1.3 : (h[i][0] - h[i - 1][1]) / 0.7;

3. 初始化

f[1] = a[1];

g[1] = a[1] + h[1][0] / 0.7;

• 代码编写：

java 复制代码

import java.util.*;
public class Main {
    public static void main(String[] args) {
        Scanner in = new Scanner(System.in);
        int n = in.nextInt();
        int[] arr = new int[n + 1];//存放杆的位置
        for(int i = 1;i <= n;i++){
            arr[i] = in.nextInt();
        }
        int[][] h = new int[n + 1][2];
        for(int i = 1;i < n;i++){
            h[i][0] = in.nextInt();
            h[i][1] = in.nextInt();
        }
        //1.创建 dp 表
        double[] f = new double[n + 1];
        double[] g = new double[n + 1];
        //2.初始化
        f[1] = arr[1];
        g[1] = arr[1] + (h[1][0]) / 0.7;

        //3.填表
        for(int i = 2;i <= n;i++){
            f[i] = Math.min(f[i - 1] + arr[i] - arr[i - 1],g[i - 1] + (h[i - 1][1]) / 1.3);
            double tmp = 0;
            if(h[i - 1][1] >= h[i][0]){
                tmp = g[i - 1] + (h[i - 1][1] - h[i][0]) / 1.3;
            }else{
                tmp = g[i - 1] + (h[i][0] - h[i - 1][1]) / 0.7;
            }
            g[i] = Math.min(f[i] + h[i][0] / 0.7,tmp);//向上爬是 0.7
        }
        //4.返回值
        System.out.printf("%.2f",f[n]);
    }
}

• 时间复杂度：

O（n），能过

• 运行结果：

六、试题 F：合并区域

• 题目分析：

题目其实不是很好读懂，题意是：随便方向都可以拼接，至少有一个接触点即可，且正方形可以翻转。考虑到要翻转，加上各个方向拼接，至少有 16 种情况以上，显然这是一道大模拟题。比赛的时候看到这种题，就暴力写点分，宁愿不写也不要全写（大佬当我没说），全部 AC 要花非常多的时间，且不一定能写对。看到大模拟就跑。

• 解题思路：

暴力大模拟，把所有翻转情况都枚举出来（填在同一个地图中），再用 bfs 找到最大连通块。我们直接把 B 填在 A 中来枚举所有情况（图中只有上下，左右没有画出），所以 A 至少要建立 3 * n的大小。在对每个 AB 分别 BFS 找出最大值，就是我们的答案。代码如果看不懂的话，画个 2 * 2的正方形，照着代码模拟一下。（翻转其中一个正方形就能枚举出所有情况）。

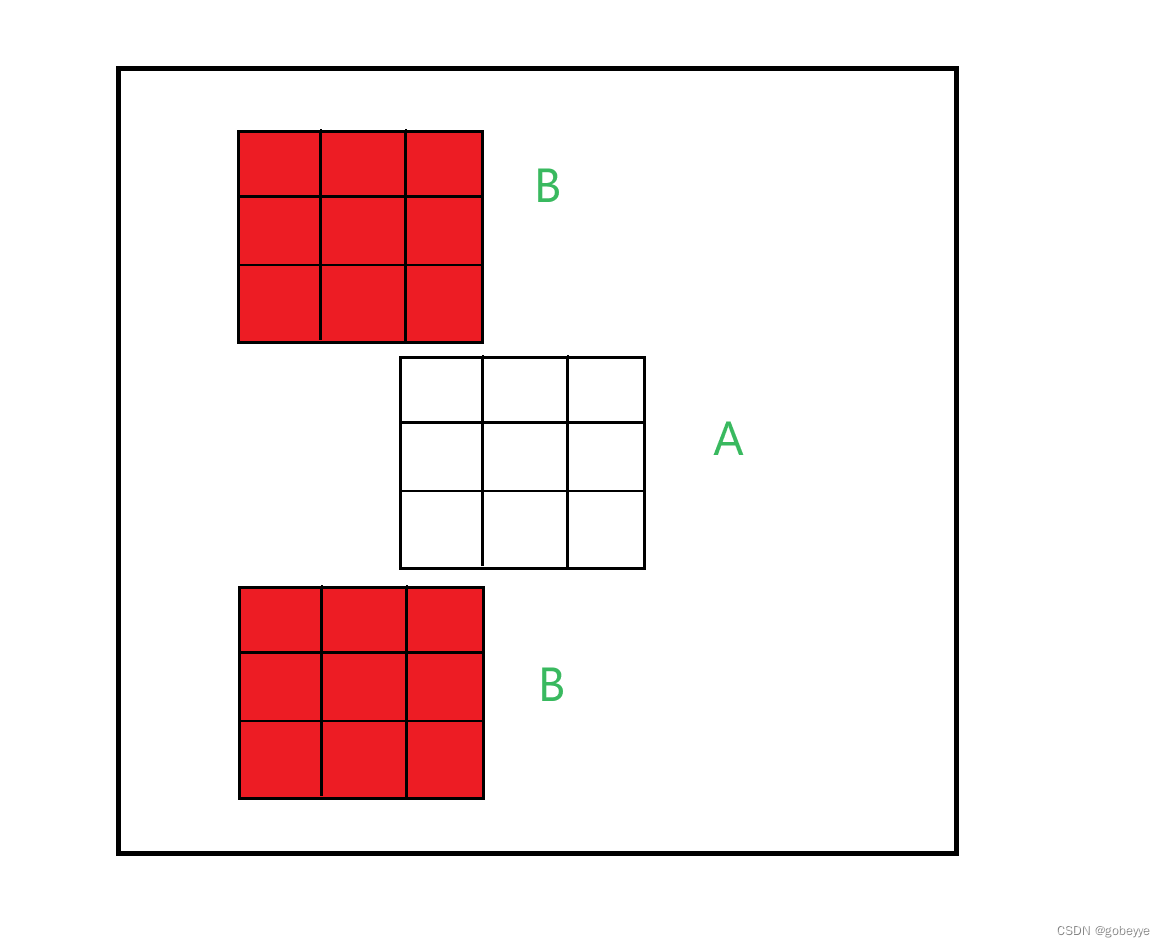
下面代码注释中的偏移位置是枚举如下图情况（左右同理）。

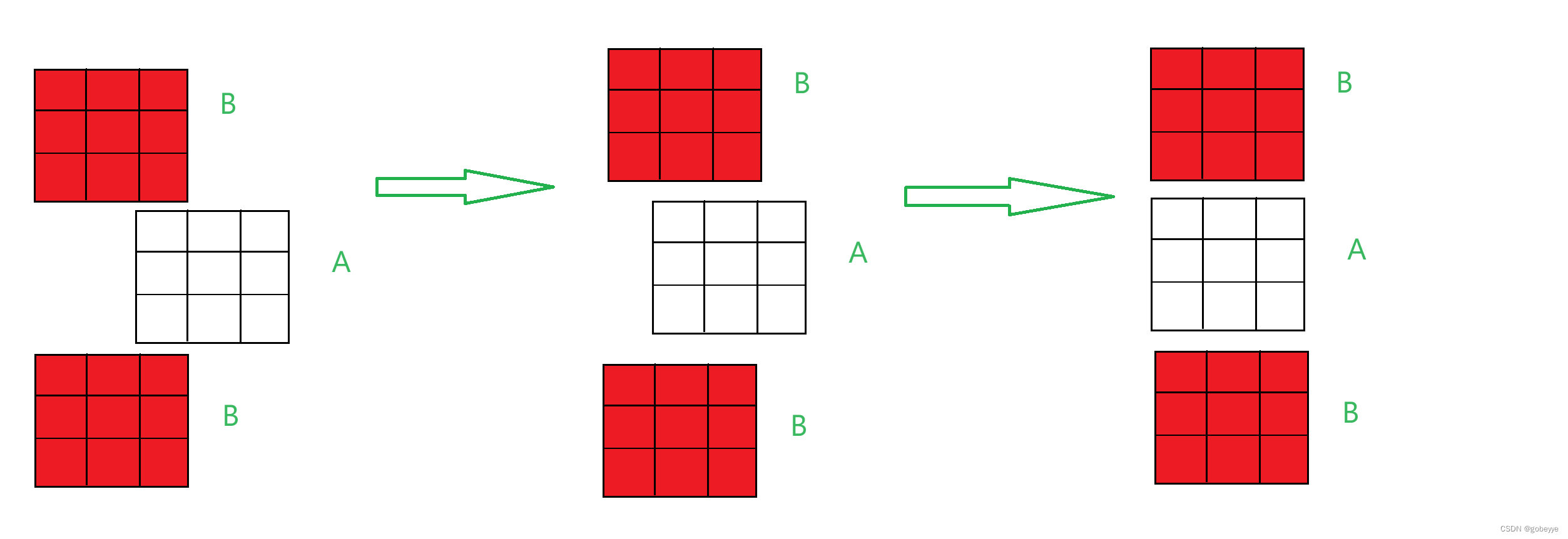
• 代码编写：

rotateMatrix 函数用来翻转矩阵（这个可以记下来）。

java 复制代码

import java.util.*;

public class Main {
    static int N = 180;//用来创建矩阵
    static int a[][] = new int[N][N];//a 用来保存最后拼接的结果
    static int b[][] = new int[55][55];// 另一个矩形
    static int n;

    public static void main(String[] args) {
        Scanner in = new Scanner(System.in);
        n = in.nextInt();
        //读入第一个矩阵
        for (int i = 1 + n; i <= n * 2; i++) {
            for (int j = 1 + n; j <= n * 2; j++) {
                a[i][j] = in.nextInt();
            }
        }
        //读入第二个矩形
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= n; j++) {
                b[i][j] = in.nextInt();
            }
        }
        int ans = 0;
        int[][] g = new int[N][N];
        for (int x = 0; x < 4; x++) {//枚举翻转的四个方向
            for (int k = 2; k <= 2 * n; k++) {//偏移位置
                for (int i = 0; i < N; i++) {
                    for (int j = 0; j < N; j++) {
                        g[i][j] = a[i][j];//将 a 拷贝给 g
                    }
                }
                for (int i = 1; i <= n; i++) {
                    for (int j = k; j <= n + k; j++) {//上下
                        g[i][j] = b[i][j - k + 1];
                        g[i + 2 * n][j] = b[i][j - k + 1];
                    }
                }
                int top = 1, bottom = 2 * n, left, right;//bfs 的边界
                if (k <= n) {
                    left = k;
                    right = 2 * n;
                } else {
                    left = n + 1;
                    right = k + n - 1;//画图
                }
                ans = Math.max(ans, bfs(g, left, right, top, bottom));//bfs 找最大联通块
                ans = Math.max(ans, bfs(g, left, right, top + n, bottom + n));
            }
            //和上面的一样不过就是填左右
            for (int k = 2; k <= 2 * n; k++) {
                for (int i = 0; i < N; i++) {
                    g[i] = Arrays.copyOf(a[i], N);
                }
                for (int i = k; i <= n + k; i++) {
                    for (int j = 1; j <= n; j++) {//填写左右
                        g[i][j] = b[i - k + 1][j];
                        g[i][j + 2 * n] = b[i - k + 1][j];
                    }
                }
                int top, bottom, left = 1, right = 2 * n;
                if (k <= n) {
                    top = k;
                    bottom = 2 * n;
                } else {
                    top = n + 1;
                    bottom = n + k - 1;
                }
                ans = Math.max(ans, bfs(g, left, right, top, bottom));
                ans = Math.max(ans, bfs(g, left + n, right + n, top, bottom));
            }
            rotateMatrix();//翻转矩阵
            for (int i = 1; i <= n; i++) {
                for (int j = 1; j <= n; j++) {
                    b[i][j] = rotate[i][j];//翻转 b 即可
                }
            }
        }
        System.out.println(ans);
    }

    static int[][] rotate = new int[N][N];

    static void rotateMatrix() {//翻转矩阵
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= n; j++) {
                rotate[j][n - i + 1] = b[i][j];
            }
        }
    }


    //简单的 bfs 求最大联通块
    static int[] dx = {0,0,1,-1};
    static int[] dy = {1,-1,0,0};
    static int bfs (int[][] map,int left,int right,int top,int bottom){
        int ret = 0;//存储最终结果
        boolean[][] vis = new boolean[N][N];
        Queue<int[]> q = new LinkedList<>();
        int path = 0;
        for(int i = top;i <= bottom;i++){
            for(int j = left;j <= right;j++){
                if(map[i][j] == 1 && !vis[i][j]){
                    path = 0;
                    q.add(new int[]{i,j});
                    while(!q.isEmpty()){
                        int[] tmp = q.poll();
                        int sr = tmp[0],sc = tmp[1];
                        path++;
                        vis[sr][sc] = true;
                        for(int k = 0;k < 4;k++){
                            int x = sr + dx[k];
                            int y = sc + dy[k];
                            if(x >= top && x <= bottom && y >= left && y <= right && !vis[x][y] &&
                            map[x][y] == 1){
                                q.add(new int[]{x,y});
                                vis[x][y] = true;
                            }
                        }
                    }
                    ret = Math.max(ret,path);
                }
            }
        }
        return ret;
    }
}

• 运行结果：

结语：

其实写博客不仅仅是为了教大家，同时这也有利于我巩固知识点，和做一个学习的总结，由于作者水平有限，对文章有任何问题还请指出，非常感谢。如果大家有所收获的话还请不要吝啬你们的点赞收藏和关注，这可以激励我写出更加优秀的文章。