本文为力扣TOP100刷题笔记
笔者根据数据结构理论加上最近刷题整理了一套 数据结构理论加常用方法以下为该文章:
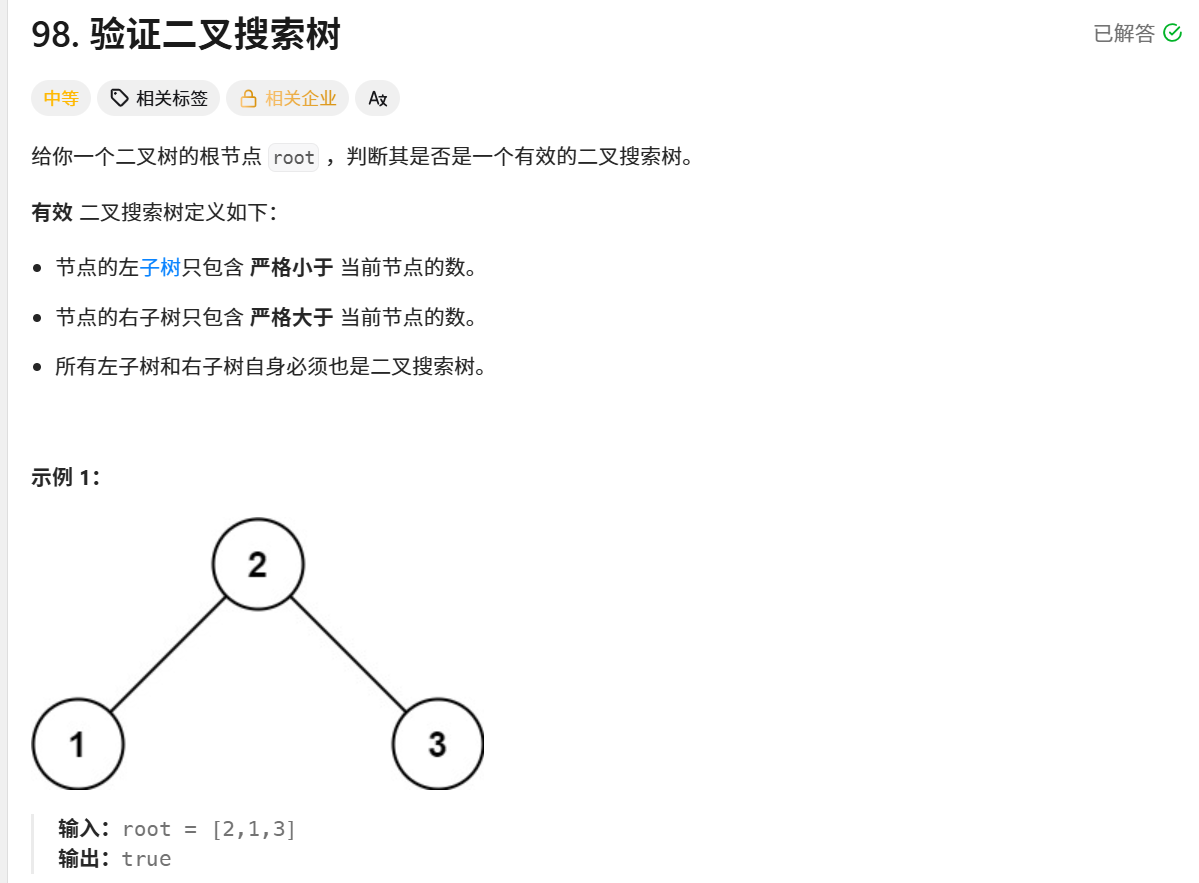
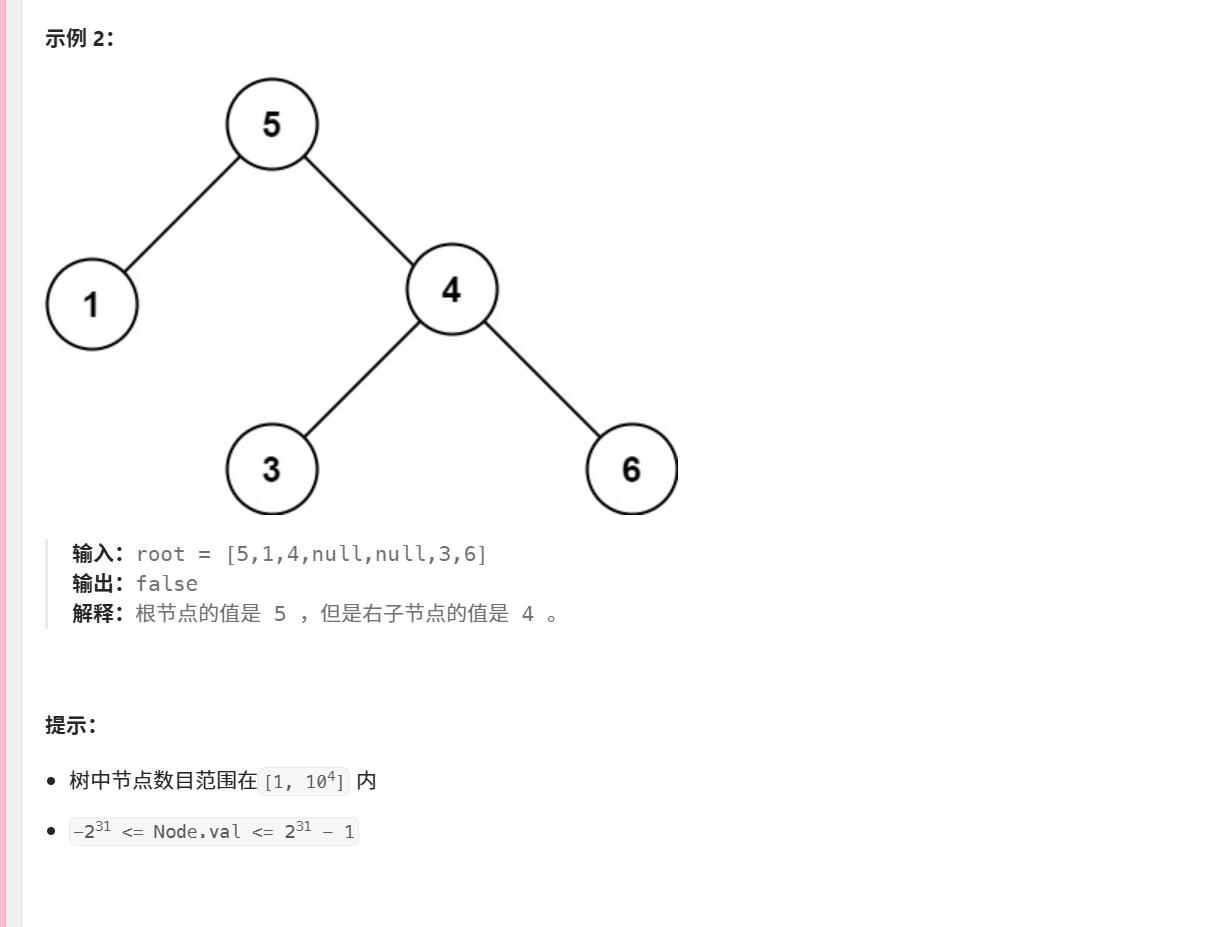
java
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public boolean isValidBST(TreeNode root) {
return treebst(root,Long.MIN_VALUE,Long.MAX_VALUE);
}
public boolean treebst(TreeNode tree,long lower, long upper){
if (tree == null) {
return true;
}
if(tree.val<=lower || tree.val>=upper){
return false;
}
return treebst(tree.left,lower,tree.val)&&treebst(tree.right,tree.val,upper);
}
}方法结构
主方法
isValidBST:
接受一个
TreeNode作为参数,表示二叉树的根节点调用辅助方法
treebst进行实际验证使用
Long.MIN_VALUE和Long.MAX_VALUE作为初始的上下界辅助方法
treebst:
参数:当前节点
tree,当前允许的最小值lower,当前允许的最大值upper递归地验证每个子树
算法逻辑
基本情况:
- 如果当前节点为
null,返回true(空树是有效的BST)验证当前节点:
检查当前节点的值是否在允许的范围内
如果
tree.val <= lower或tree.val >= upper,返回false这确保了BST的性质:左子树所有节点必须小于当前节点,右子树所有节点必须大于当前节点
递归验证子树:
对于左子树:上限变为当前节点的值,下限保持不变
对于右子树:下限变为当前节点的值,上限保持不变
只有当左右子树都有效时,当前树才有效
关键点
使用长整型边界 :防止节点值等于
Integer.MIN_VALUE或Integer.MAX_VALUE时出现边界问题递归传递边界:在递归过程中不断缩小允许的值范围
前序遍历:先检查当前节点,再递归检查左右子树
时间复杂度
O(n):需要访问树中的每个节点一次
空间复杂度:O(h),其中h是树的高度(递归调用栈的深度)
这个算法高效地验证了BST的性质,确保左子树所有节点小于父节点,右子树所有节点大于父节点。
230. 二叉搜索树中第 K 小的元素
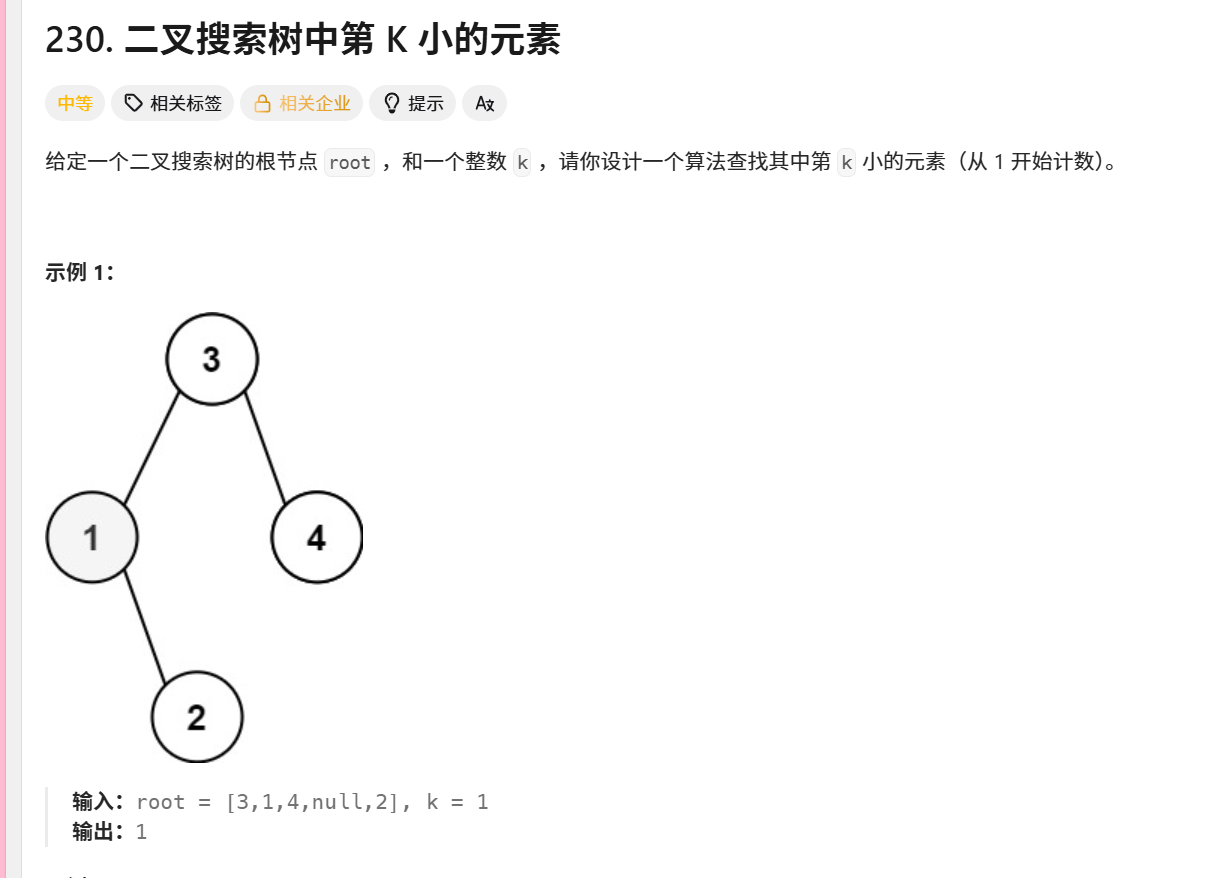
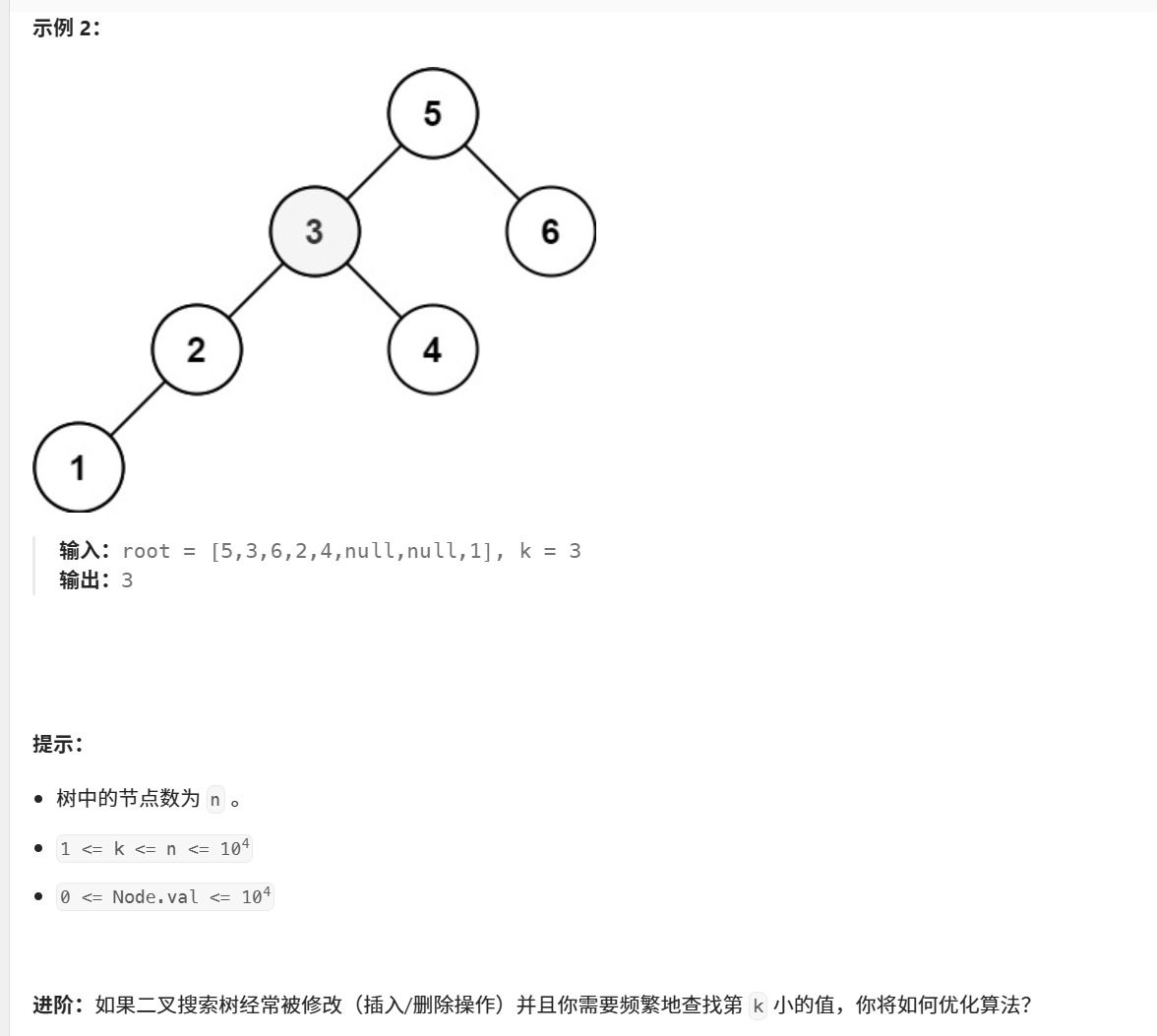
java
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public int kthSmallest(TreeNode root, int k) {
// 使用双端队列作为栈来存储节点
Deque<TreeNode> stack = new ArrayDeque<TreeNode>();
// 循环条件:当前节点不为空或栈不为空
while (root != null || !stack.isEmpty()) {
// 一直向左遍历,将所有左节点压入栈
while (root != null) {
stack.push(root);
root = root.left;
}
// 弹出栈顶节点(当前最小节点)
root = stack.pop();
// 计数器递减
--k;
// 如果k减到0,说明找到了第k小的元素
if (k == 0) {
break;
}
// 转向右子树
root = root.right;
}
// 返回当前节点的值(此时k=0)
return root.val;
}
}关键点解释
栈的使用:
使用
Deque作为栈来模拟递归调用的系统栈每次将左子节点压入栈,直到最左端
中序遍历过程:
外层
while循环控制整体遍历内层
while循环负责一直向左遍历
pop()操作对应访问当前最小节点
root = root.right转向右子树k的处理:
每访问一个节点,k减1
当k减到0时,当前节点就是第k小的元素
示例演示
考虑BST:
text
5 / \ 3 6 / \ 2 4 / 1查找第3小的元素:
栈:[5,3,2,1],访问1,k=2
弹出1,访问2,k=1
弹出2,访问3,k=0 → 找到第3小的元素3
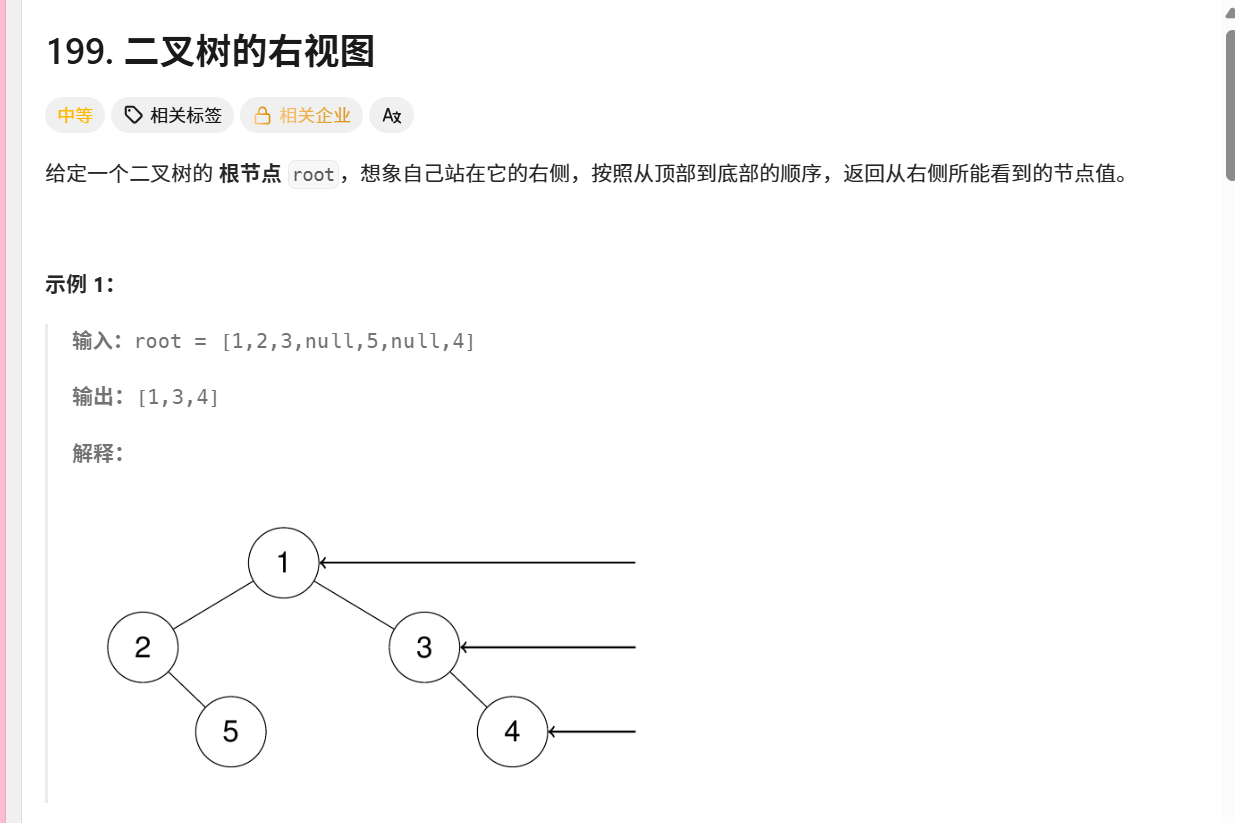
199. 二叉树的右视图
java
public List<Integer> rightSideView(TreeNode root) {
// 存储每个深度对应的最右侧节点值
Map<Integer, Integer> rightmostValueAtDepth = new HashMap<Integer, Integer>();
// 记录最大深度
int max_depth = -1;
// 使用两个栈分别存储节点和对应的深度
Deque<TreeNode> nodeStack = new LinkedList<TreeNode>();
Deque<Integer> depthStack = new LinkedList<Integer>();
// 初始化栈
nodeStack.push(root);
depthStack.push(0);
while (!nodeStack.isEmpty()) {
TreeNode node = nodeStack.pop();
int depth = depthStack.pop();
if (node != null) {
// 更新最大深度
max_depth = Math.max(max_depth, depth);
// 只有当该深度尚未记录时才存入(保证记录的是该深度最后访问的节点)
if (!rightmostValueAtDepth.containsKey(depth)) {
rightmostValueAtDepth.put(depth, node.val);
}
// 注意压栈顺序:先左后右,出栈时就是先右后左
nodeStack.push(node.left);
nodeStack.push(node.right);
depthStack.push(depth + 1);
depthStack.push(depth + 1);
}
}
// 按照深度顺序构建结果列表
List<Integer> rightView = new ArrayList<Integer>();
for (int depth = 0; depth <= max_depth; depth++) {
rightView.add(rightmostValueAtDepth.get(depth));
}
return rightView;
}关键点解释
双栈结构:
nodeStack存储待访问的节点
depthStack存储对应节点的深度两个栈同步操作,保证节点和深度对应
右视图记录策略:
使用HashMap按深度记录节点值
每个深度只记录第一个访问到的节点(由于栈是后进先出,先压左节点后压右节点,所以右节点会先被访问)
遍历顺序:
虽然是DFS,但通过栈的压入顺序实现了"右节点优先"的访问顺序
先压左子节点,后压右子节点,保证右子节点先出栈被访问
示例演示
考虑二叉树:
text
1 / \ 2 3 \ \ 5 4右视图应为[1, 3, 4]
执行过程:
深度0:记录1
深度1:先访问3(右节点),再访问2(但深度1已记录)
深度2:先访问4(右节点),再访问5(但深度2已记录)
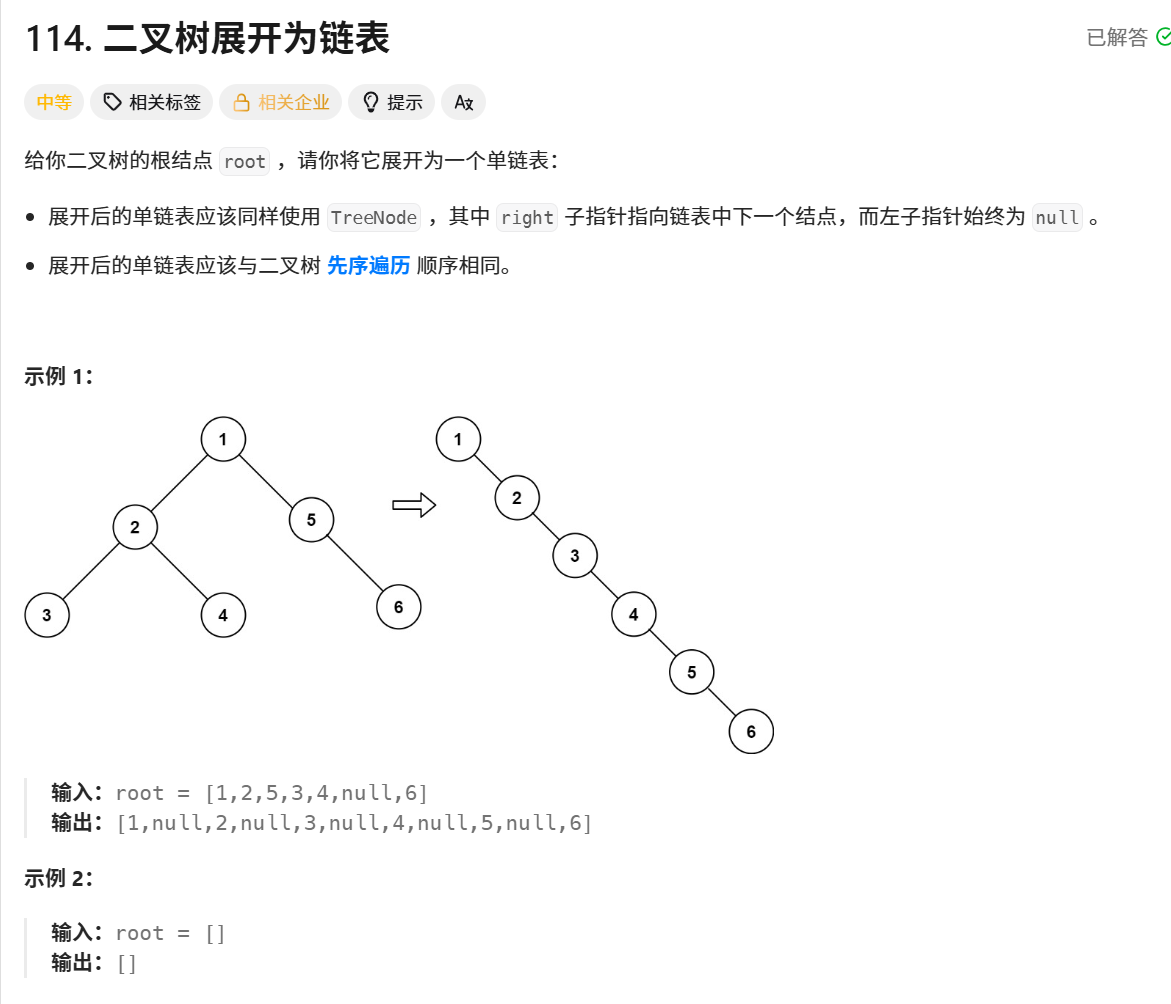
114. 二叉树展开为链表
java
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public void flatten(TreeNode root) {
// 存储前序遍历结果的列表
List<TreeNode> list = new ArrayList<TreeNode>();
// 执行前序遍历,填充列表
preorderTraversal(root, list);
int size = list.size();
// 将列表中的节点连接成链表
for (int i = 1; i < size; i++) {
TreeNode prev = list.get(i - 1); // 前一个节点
TreeNode curr = list.get(i); // 当前节点
prev.left = null; // 左指针置空
prev.right = curr; // 右指针指向当前节点
}
}
// 递归前序遍历辅助方法
public void preorderTraversal(TreeNode root, List<TreeNode> list) {
if (root != null) {
list.add(root); // 访问当前节点
preorderTraversal(root.left, list); // 遍历左子树
preorderTraversal(root.right, list); // 遍历右子树
}
}
}关键点解释
前序遍历收集节点:
使用递归前序遍历(根-左-右顺序)将所有节点按顺序存入列表
列表中的节点顺序就是最终链表的顺序
链表重构:
遍历节点列表,将每个节点的左指针置为null
将前一个节点的右指针指向当前节点
最终形成只有右指针的单链表结构
原地修改:
直接修改原二叉树的结构,不创建新节点
所有操作都在原节点上进行
示例演示
给定二叉树:
text
1 / \ 2 5 / \ \ 3 4 6执行过程:
前序遍历结果列表:[1,2,3,4,5,6]
重构链表:
1.right=2, 1.left=null
2.right=3, 2.left=null
3.right=4, 3.left=null
...
最终链表:1→2→3→4→5→6
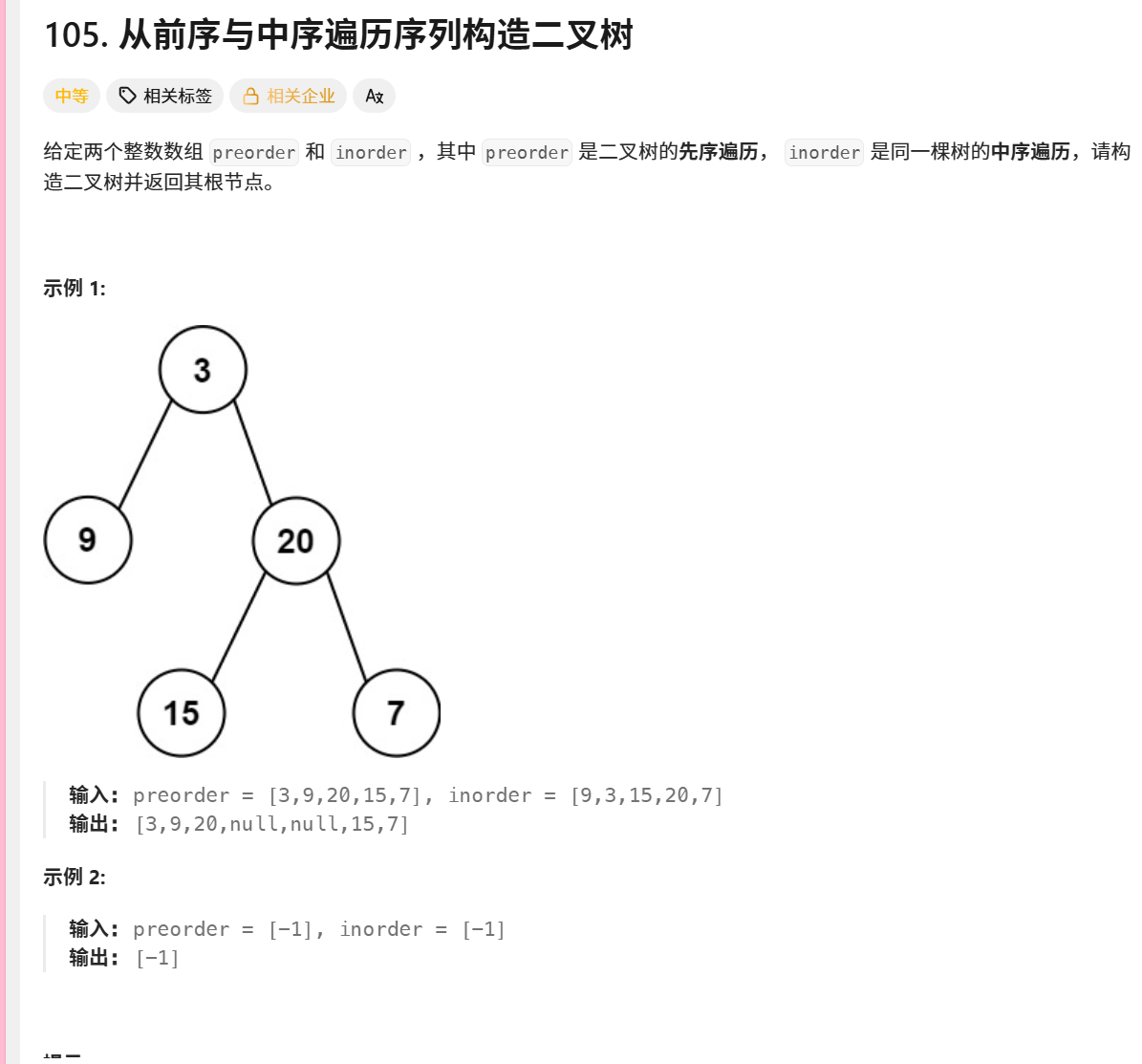
105. 从前序与中序遍历序列构造二叉树
java
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
private Map<Integer, Integer> indexMap;
public TreeNode myBuildTree(int[] preorder, int[] inorder, int preorder_left, int preorder_right, int inorder_left, int inorder_right) {
if (preorder_left > preorder_right) {
return null;
}
// 前序遍历中的第一个节点就是根节点
int preorder_root = preorder_left;
// 在中序遍历中定位根节点
int inorder_root = indexMap.get(preorder[preorder_root]);
// 先把根节点建立出来
TreeNode root = new TreeNode(preorder[preorder_root]);
// 得到左子树中的节点数目
int size_left_subtree = inorder_root - inorder_left;
// 递归地构造左子树,并连接到根节点
// 先序遍历中「从 左边界+1 开始的 size_left_subtree」个元素就对应了中序遍历中「从 左边界 开始到 根节点定位-1」的元素
root.left = myBuildTree(preorder, inorder, preorder_left + 1, preorder_left + size_left_subtree, inorder_left, inorder_root - 1);
// 递归地构造右子树,并连接到根节点
// 先序遍历中「从 左边界+1+左子树节点数目 开始到 右边界」的元素就对应了中序遍历中「从 根节点定位+1 到 右边界」的元素
root.right = myBuildTree(preorder, inorder, preorder_left + size_left_subtree + 1, preorder_right, inorder_root + 1, inorder_right);
return root;
}
public TreeNode buildTree(int[] preorder, int[] inorder) {
int n = preorder.length;
// 构造哈希映射,帮助我们快速定位根节点
indexMap = new HashMap<Integer, Integer>();
for (int i = 0; i < n; i++) {
indexMap.put(inorder[i], i);
}
return myBuildTree(preorder, inorder, 0, n - 1, 0, n - 1);
}
}关键点解释
哈希映射优化:
预处理中序遍历数组,建立值到索引的映射
使得在中序遍历中查找根节点位置的时间降为O(1)
递归构建过程:
前序遍历的第一个元素总是当前子树的根节点
在中序遍历中定位该根节点,左侧为左子树,右侧为右子树
根据左子树节点数量确定前序遍历中左右子树的分界
索引范围计算:
前序遍历左子树范围:
[pre_left+1, pre_left+left_size]前序遍历右子树范围:
[pre_left+left_size+1, pre_right]中序遍历左子树范围:
[in_left, in_root-1]中序遍历右子树范围:
[in_root+1, in_right]示例演示
给定:
前序遍历 preorder = [3,9,20,15,7]
中序遍历 inorder = [9,3,15,20,7]
构建过程:
根节点3(前序第一个)
在中序中找到3,左侧[9]是左子树,右侧[15,20,7]是右子树
递归构建:
左子树:前序[9],中序[9]
右子树:前序[20,15,7],中序[15,20,7]
最终树结构:
text
3 / \ 9 20 / \ 15 7
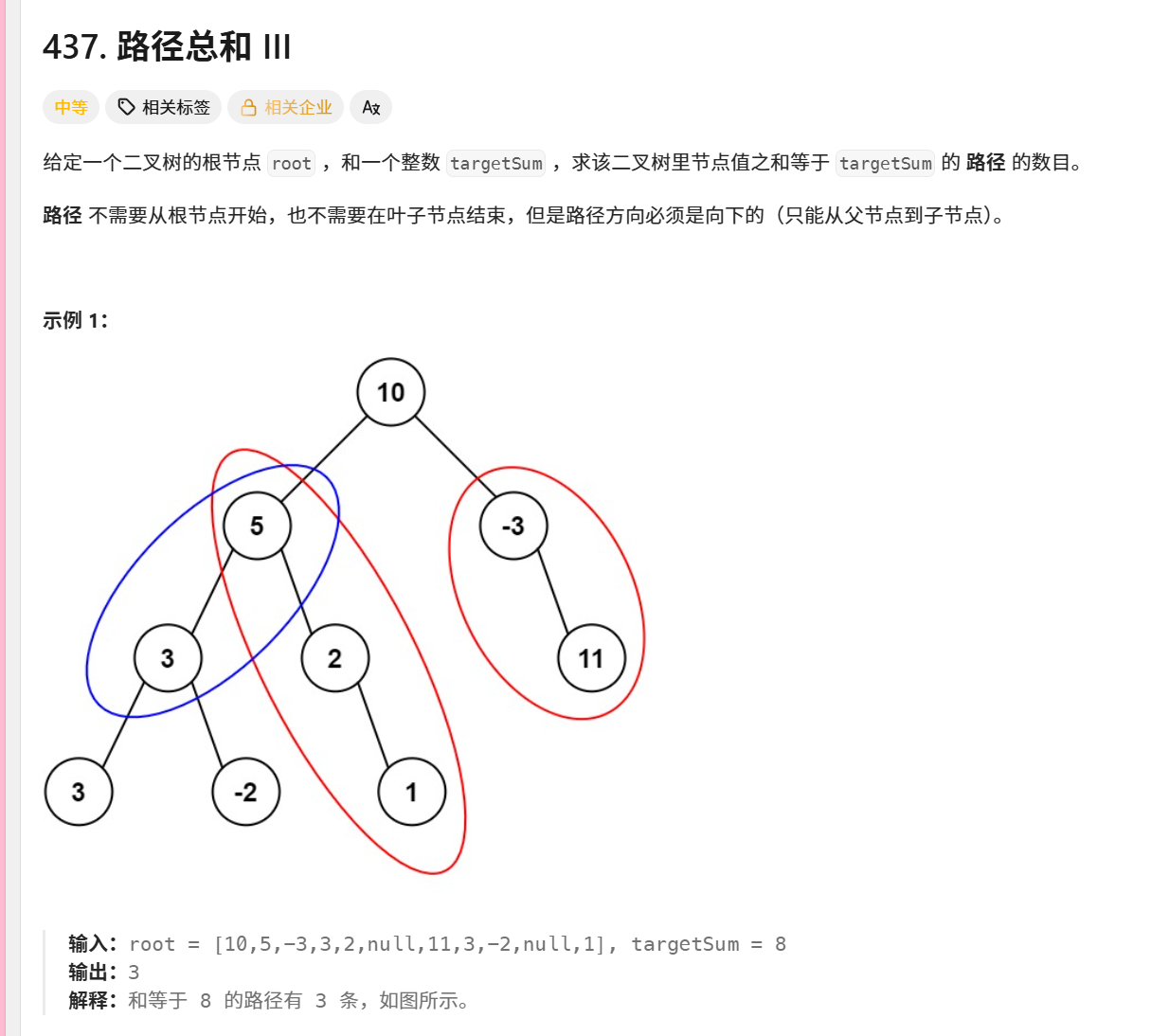
437. 路径总和 III

java
class Solution {
// 主方法:计算所有路径和等于targetSum的数量
public int pathSum(TreeNode root, long targetSum) {
if (root == null) {
return 0;
}
// 计算以当前节点为起点的路径数量
int ret = rootSum(root, targetSum);
// 递归计算左子树的所有可能路径
ret += pathSum(root.left, targetSum);
// 递归计算右子树的所有可能路径
ret += pathSum(root.right, targetSum);
return ret;
}
// 辅助方法:计算以当前节点为起点的路径和等于targetSum的数量
public int rootSum(TreeNode root, long targetSum) {
int ret = 0;
if (root == null) {
return 0;
}
int val = root.val;
// 如果当前节点值等于剩余目标值,找到一条路径
if (val == targetSum) {
ret++;
}
// 递归检查左子树,更新剩余目标值
ret += rootSum(root.left, targetSum - val);
// 递归检查右子树,更新剩余目标值
ret += rootSum(root.right, targetSum - val);
return ret;
}
}关键点解释
双重递归结构:
pathSum():遍历树的所有节点,将每个节点作为路径起点
rootSum():计算以给定节点为起点的所有满足条件的路径数量路径计算逻辑:
每当路径和等于目标值时计数器加1
继续向下搜索,因为可能有正负值抵消的情况(如路径1→-1→1的和为1)
递归终止条件:
当前节点为null时返回0
不要求路径结束于叶子节点
示例演示
给定二叉树:
text
10 / \ 5 -3 / \ \ 3 2 11 / \ \ 3 -2 1目标值:8
执行过程:
从10开始:10→5→3(和为18,不等于8),继续向下...
从5开始:5→3(和为8,计数+1),5→3→-2(和为6),5→2→1(和为8,计数+1)
从3开始:3→3(和为6),3→-2(和为1)
从-3开始:-3→11(和为8,计数+1)
最终找到3条路径:[5,3]、[5,2,1]、[-3,11]
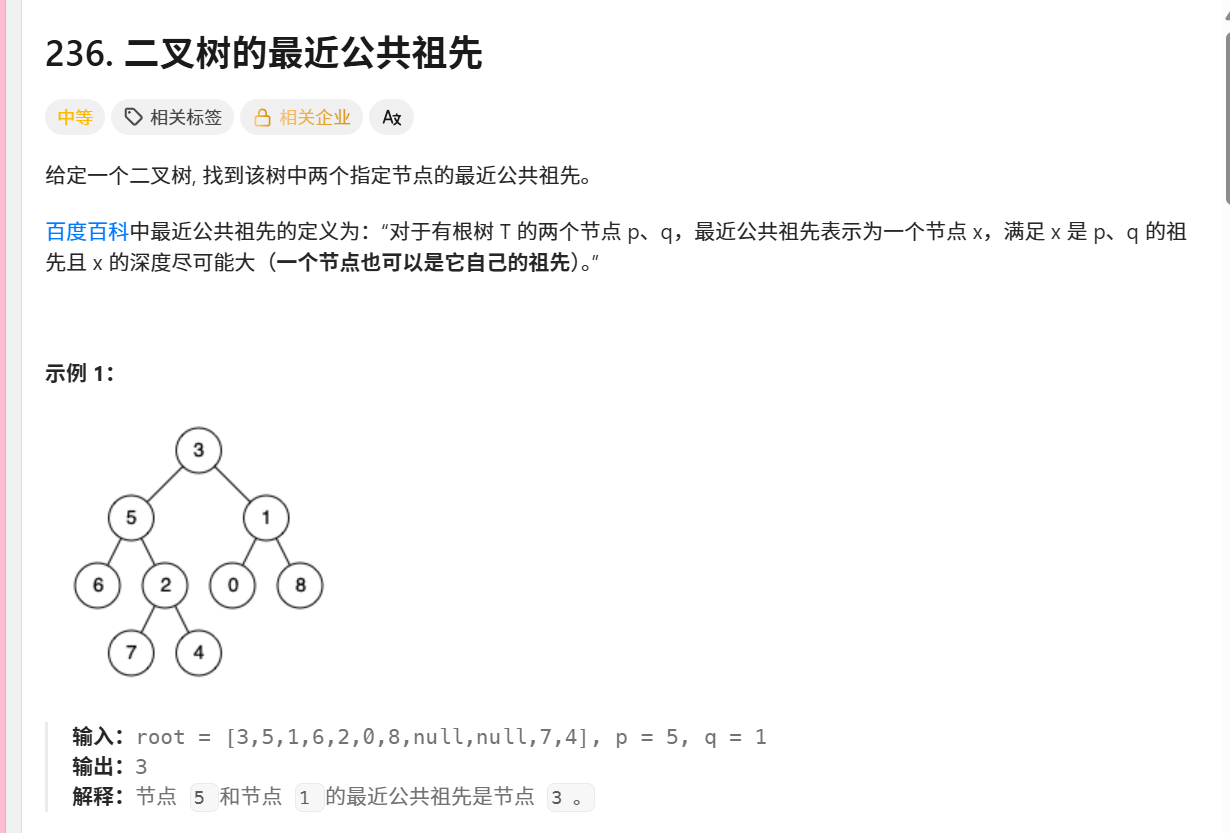
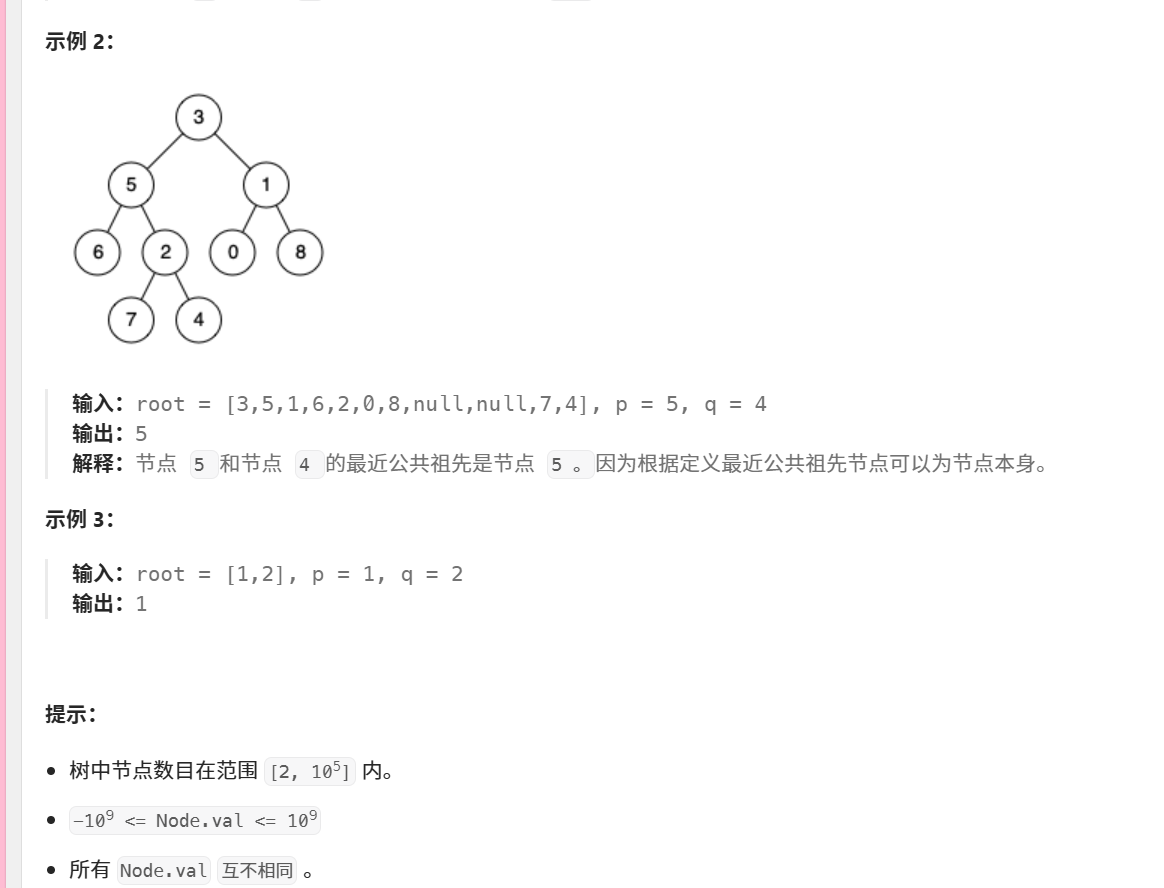
236. 二叉树的最近公共祖先
java
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
private TreeNode ans;
public Solution() {
this.ans = null;
}
private boolean dfs(TreeNode root, TreeNode p, TreeNode q) {
if (root == null) return false;
boolean lson = dfs(root.left, p, q);
boolean rson = dfs(root.right, p, q);
if ((lson && rson) || ((root.val == p.val || root.val == q.val) && (lson || rson))) {
ans = root;
}
return lson || rson || (root.val == p.val || root.val == q.val);
}
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
this.dfs(root, p, q);
return this.ans;
}
}关键点解释
递归终止条件:
当前节点为null时返回false
表示当前路径不包含目标节点
LCA判断条件:
情况1:左右子树分别包含p和q(
lson && rson)情况2:当前节点是p或q,且另一个节点在子树中
满足任一条件即记录当前节点为LCA
返回值意义:
返回布尔值表示当前子树是否包含p或q
用于向上传递节点存在信息
示例演示
给定二叉树:
text
3 / \ 5 1 / \ / \ 6 2 0 8 / \ 7 4查找节点5和1的LCA:
递归到节点3时:
左子树包含5(lson=true)
右子树包含1(rson=true)
满足
lson && rson,记录3为LCA查找节点5和4的LCA:
递归到节点5时:
自身是5
右子树包含4(rson=true)
满足条件2,记录5为LCA