数据结构与算法笔记：高级篇 - B+树：MySql数据库索引是如何实现的？

概述

作为一名软件开发工程师，你对数据库肯定再熟悉不过了。MySQL 作为主流的数据库存储系统，它在我们的业务开发中，有着举足轻重的地位。在工作中，为了加速数据库中数据的查找速度，我们常用的处理思路是，对表中的数据创建索引。那你是否考虑过，数据库索引是如何实现的呢？底层使用的是什么数据结构和算法呢？

算法解析

思考的过程比结论重要，本章会尽量还原这个解决方案的思考过程，让你知其然，并知其所以然。

1.解决问题的前提是定义清楚问题

如何定义清楚问题呢？除了对问题进行详细的调研，还有一个办法，那就是，通过对一些模糊的需求进行假设，来限定要解决的问题的范围。

如果你对数据库的操作非常了解，针对我们现在这个问题，你就能把索引的需求定义得非常清楚。但是，对于大部分软件工程师来说，我们可能只了解一小部分常用的 SQL 语句，所以，我们这里假设要解决的问题，只包含这样两个常用的需求：

根据某个值查找数据，比如 select * from user where id = 1234。
根据区间来查找某些数据，比如 select * from user where id > 1234 and id < 2345。

除了这些功能性需求之外，这种问题往往还会涉及一些非功能性需求，比如安全、性能、用户体验等等。限于本章要讨论的是数据结构和算法，对于非功能性需求，我们着重考虑性能方面 的需求。性能方面的需求，我们主要考察时间和空间两方面，也就是执行效率和存储空间。

在执行效率方面，我们系统通过索引，查询数据的效率尽可能地高；在存储空间方面，我们希望索引不要消耗太多的内存空间。

2.尝试用学过的数据结构解决这个问题

问题的需求大致定义清楚了，现在回想一下，能否利用已经学习过的数据结构解决这个问题呢？支持快速查询、插入等操作的动态数据结构，我们学习过散列表、平衡二叉查找树、跳表。

先来看散列表 。散列表的查询性能很好，时间复杂度是 O ( 1 ) O(1) O(1)。但是，散列表不支持按区间快速查找数据。所以，散列表不能满足我们的需求。

再看下平衡二叉查找树 。尽管平衡二叉查找树查询的性能也很高，时间复杂度是 O ( l o g n ) O(logn) O(logn)。而且，对数进行中序遍历，还可以得到一个从小到大的有序的数据序列，但仍然不足以支持按照区间快速查找数据。

最后看下跳表。跳表是在链表之上加上多层索引构成的。它支持快速插入、查找、删除数据，对应的时间复杂度是 O ( l o g n ) O(logn) O(logn)。并且跳表也支持按区间快速查找数据。我们只需要定位区间的起点值对应在链表中的位置，然后从这个节点开始，顺序遍历链表，直到区间终点对应的结点为止，这期间遍历得到的数据就是满足区间值的数据。

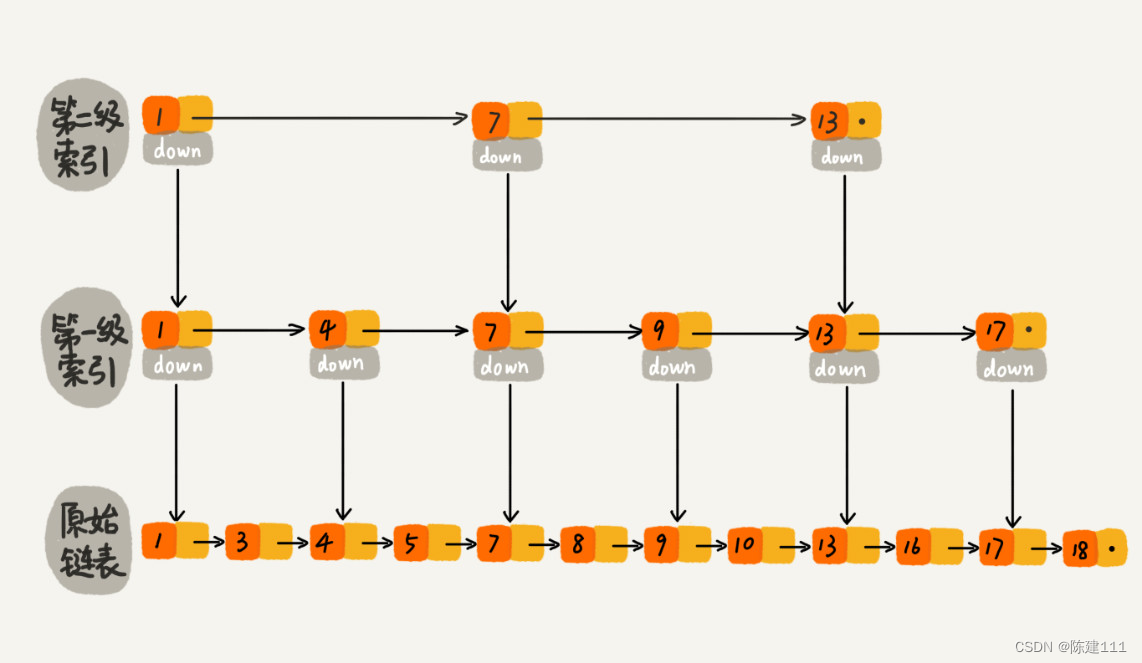
这样看来，跳表是可以解决这个问题。实际上，数据库索引所用到的数据结构跟跳表非常相似，叫作 B+ 树。不过，它是通过二叉查找树演化过来的，而非跳表。为了给你还原发明 B+ 树的整个思考过程，所以，接下来，我还要从二叉查找树将其，看它是如何一步一步被改造成 B+ 树的。

改造二叉查找树来解决这个问题

为了让二叉查找树支持按照区间来查找数据，我们可以对它进行这样的改造：树中的节点并不存储数据本身，而是只是作为索引。此外，我们把每个叶子节点串在一条链表上，链表中的数据时从小到大有序的。经过改造之后的二叉树，就像图中这样，看起来是不是很像跳表。

改造之后，如果我们要求某个区间的数据。我们只需要拿到区间的起始值，在树中进行查找，当查找到某个叶子节点后，我们再顺着链表往后遍历，直到链表中的节点数据值大于区间的终止值为止。所有遍历的数据，就是符合区间值的所有数据。

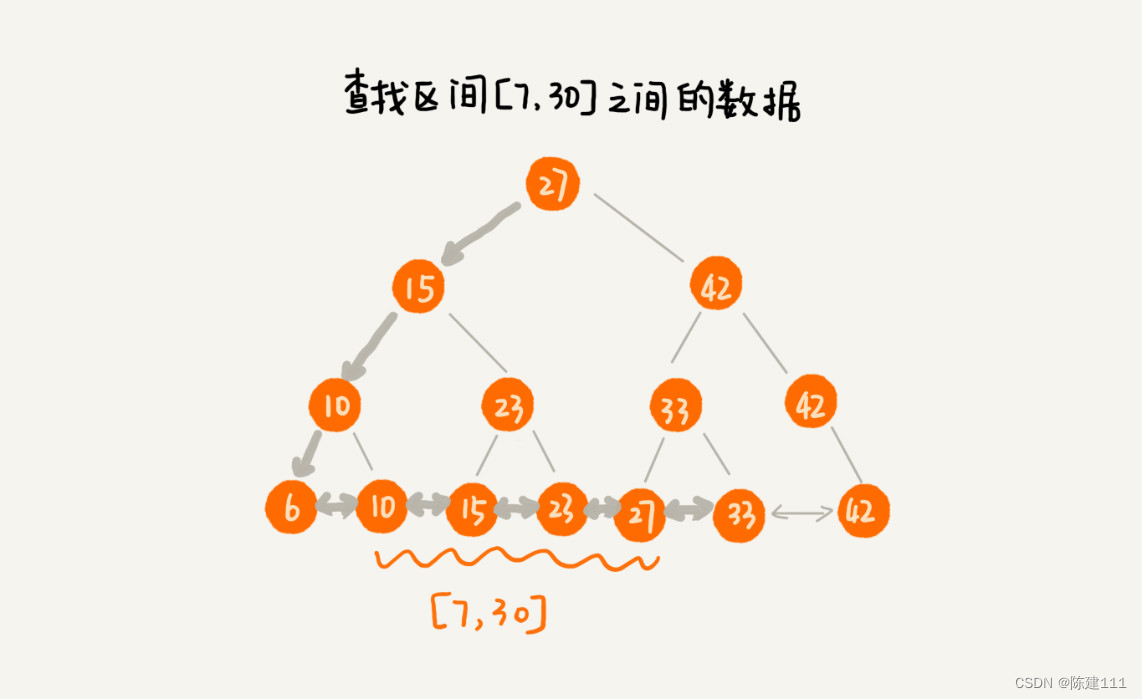
但是，我们要为几千万、上亿的数据构建索引，如果将索引存储在内存中，尽管内存访问的速度非常快，查询的效率非常高，但是，占用的内存会非常多。

比如，我们给一亿个数据构建二级索引，那索引中会保护大约 1 亿个节点，每个节点假设占 16 个字节，那就需要大约 1GB 的内存空间。给一张表建立索引，我们需要 1GB 的内存空间。如果我们要给 10 张表构建索引，那对内存的需求是无法满足的。如何解决索引占用太多内存这个问题呢？

我们可以借助时间换空间的思路，把索引存储到磁盘中，而非内存中。我们都知道，硬盘是一个非常慢速的存储设备。通常内存的访问速度是纳秒级的，而磁盘的访问速度是毫秒级别的。读取同样大小的数据，从磁盘总读取花费的时间，是从内存中读取所花费时间的上万倍，甚至几十万倍。

这种将索引存储在磁盘中的方案，尽管减少了内存消耗，但是在查找数据的过程中，需要读取磁盘中的索引，因此数据查询效率就相应降低很多。

二叉查找树经过改造之后，支持区间查找的功能实现了。不过，为了节省内存，如果把树存储在硬盘中，那么每个节点的读取（或者访问），都对应一次磁盘 IO 操作。树的高度就等于每次查询数据时磁盘 IO 操作的次数。

前面说过，比起内存读写操作，磁盘 IO 操作非常耗时，所以我们优化的重点就是尽量减少磁盘 IO 的次数，也就是尽量降低树的高度。那如何降低树的高度呢？

我们来看下，如果我们把索引构建成 m 叉树，高度是不是比二叉树要小呢？如图所示，给 16 个数据构建二叉树索引，树的高度是 4，查找一个数据，需要 4 个磁盘 IO 操作（如果根节点存储子内存中，其他节点存储在磁盘中），如果对 16 个数据构建五叉树索引，那高度只有 2，查找一个数据，对应只需要 2 次磁盘操作。如果 m 叉树中的 m 是 100，那对一亿个数据构建索引，树的高度也只是 3，最多只要 3 次磁盘 IO 就能获取到数据。磁盘 IO 变少了，查找数据的效率也就提高了。

如果我们将 m 叉树实现 B+ 树索引，用代码实现出来，就是下面这样刚子（假设我们给 int 类型的数据库字段添加索引，所以代码中的 keywords 是 int 类型的）。

java 复制代码

/**
 * 这是B+树非叶子节点的定义
 *
 * 假设keywords=[3, 5, 8, 10]
 * 4个键值将数据分为5个区间：（-INF,3), [3,5), [5,8), [8,10), [10,INF)
 * 5个区间分别对应： children[0]...children[4]
 *
 * m值是事先计算得到的，计算的依据是让所有信息的大小正好等于页的大小：
 * PAGE_SIZE = (m-1)*4[keywords大小] + m*8[children大小]
 */
public class BPlusTreeNode {
    public static int m = 5; // 5叉树
    public int[] keywords = new int[m-1]; // 键值，用来划分数据区间
    public BPlusTreeNode[] children = new BPlusTreeNode[m]; // 保存子节点指针
}

/**
 * 这是B+树的叶子节点的定义。
 *
 * B+树中的叶子节点跟内部节点是不一样的
 * 叶子节点存储的是值，而非区间。
 * 这个定义里，每个叶子节点存储3个数据行的键值及地址信息。
 *
 * k是事先计算得到的，计算的基于是让所有信息的大小正好等于页的大小
 * PAGE_SIZE = k*4[keywords大小] + k*8[dataAddress大小]+8[prev大小]+8[next大小]
 */
public class BPlusTreeLeafNode {
    public static int k = 3;
    public int[] keywords = new int[k]; // 数据的键值
    public long[] dataAddress = new long[k]; // 数据地址

    public BPlusTreeLeafNode prev; // 这个节点在链表中的前驱节点
    public BPlusTreeLeafNode next; // 这个节点在链表中的后继节点
}

我稍微解释下这段代码。

对于相同个数的数据构建 m 叉索引，m 叉树中的 m 越大，那树的高度就越小，那 m 叉树中的 m 是不是越大就越好呢？到底多大才最合适呢？

不管是内存中的数据，还是磁盘中的数据，操作系统都是按页（一页大小通常是 4KB，这个值可以通过 getconfig PAGE_SIZE 命令查看）来读取，一次会读一页的数据。如果读取的数据量超过一页的大小，就会触发多次 IO 操作。所以，我们在选择 m 大小的时候，要尽量让每个节点大小等于一个页的大小。读取一个节点，只需要一次磁盘 IO 操作。

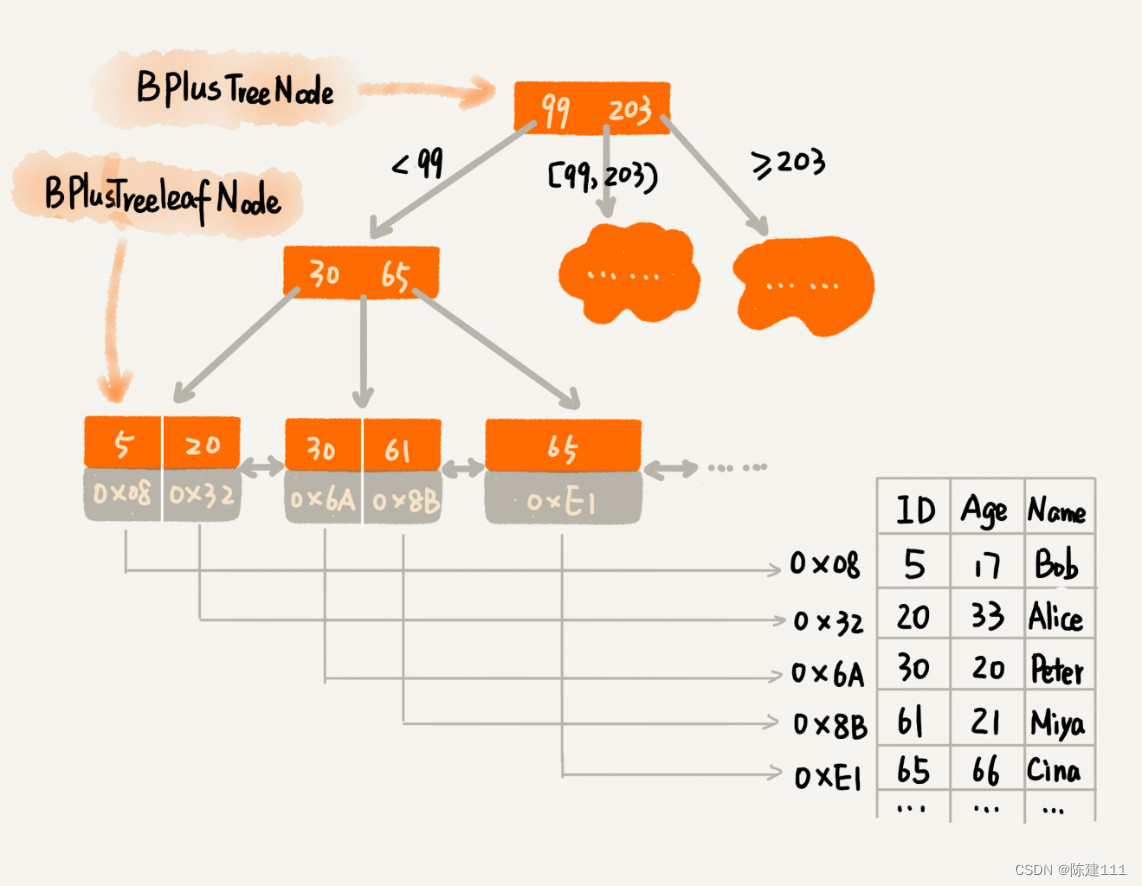
正式因为要时刻保证 B+ 树索引是一个 m 叉树，所以，索引的存在会导致数据写入的速度降低。实际上，不光写入数据会变慢，删除数据也会变慢。这是为什么呢？

我们在删除某个数据时，也要对应的更新索引节点。这个处理思路有点类似跳表中删除数据的处理思路。频繁的数据删除，就会导致某个子节点中，子节点的个数变得非常少，长此以往，如果每个节点的子节点都比较少，势必会影响索引的效率。

我们可以设置一个阈值。在 B+ 树中，阈值等于 m/2。如果某个节点的子节点个数小于 m/2，我们就将他跟相邻的兄弟节点合并。不过，合并之后的节点个数有可能超过 m。针对这种情况，我们可以借助插入数据时候的处理方法，再分裂节点。

文字描述不是很直观，我举了一个删除操作的例子，你对比看下（图中的 B+ 树是一个五叉树。我们限定叶子节点中，数据的个数少于 2 个就合并节点；非叶子节点中，子节点的个数少于 3 个就合并节点）。

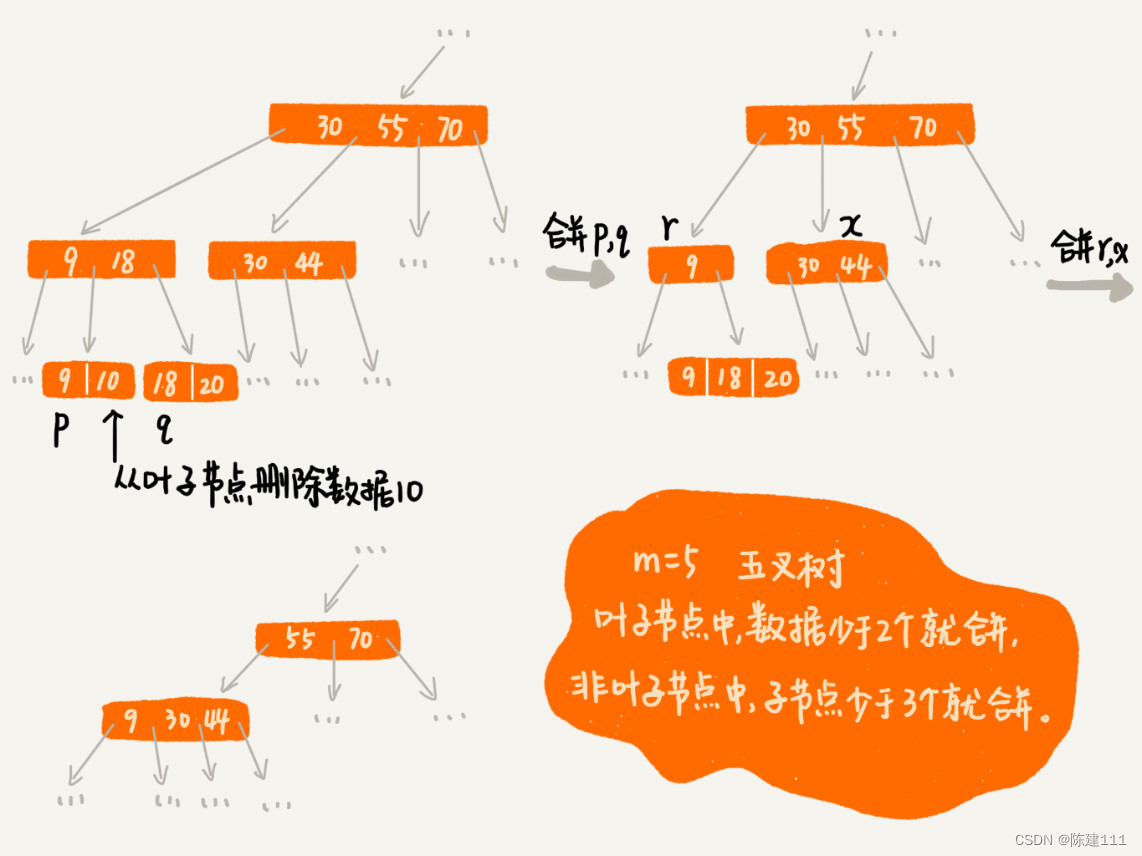
数据库索引以及 B+ 树的由来，至此就讲完了。你有没有发现，B+ 树的结构和操作，跟跳表非常类似。理论上将，对跳表稍加改造，也可以替换 B+ 树，作为数据的索引实现。

B+ 树发明与 1972 年，跳表发明与 1989 年，我们可以大胆猜想下，跳表的作者可能就是受到了 B+ 树的启发，才发明出跳表来的。不过，这个也无从考证了。

总结

本章，讲解了数据库索引的实现，依赖的底层数据结构，B+ 树。它通过存储在磁盘的多叉树结构，做到了时间、空间的平衡，既保证了执行效率，又节省了内存。

前面的讲解中，为一步一步详细地给你介绍 B+ 树的由来，内容看起来比较零散。为了方便你掌握和记忆，这里再总结一下 B+ 树的特点：

每个叶子节点中子节点的个数不能超过 m，也不能小于 m/2。
根节点的子节点个数可以不超过 m/2，这是一个例外。
m 叉树只存储索引，并不真正存储数据，这个有点而类似跳表。
通过链表将叶子节点串联在一起，这样可以方便按区间查找。
一般情况，根节点会被存储在内存中，其他节点存储在磁盘中。

除了 B+ 树，你可能还听说过 B 树、B- 树，这里简单提一下。实际上 B- 树就是 B 树，英文翻译为 B-Tree，这里的 "-" 并不是相对 B+ 树中的 "+"，而只是一个连接符。这个很容易误解，所以我强调下。

而 B 树实际上是低级版的 B+ 树，或者说 B+ 树是 B 树的改进版。B 树跟 B+ 树的不同点主要集中在这几个地方：

B+ 树中的节点不存储数据，只存储索引，而 B 树中的节点存储数据；
B 树中的叶子节点并不需要链表来串联。

也就是说，B 树只是一个每个叶子节点个数不能小于 m/2 的 m 叉树。