灰色预测是对时间有关的灰色过程进行预测。通过建立相应的微分方程模型,从而预测事物未来发展趋势的状况。
由于笔者的水平不足,本章只是概括性地介绍GM(1,1)模型的理论原理,便于对初学者的初步理解
目录
一、灰色系统

二、GM(1,1)灰色预测模型
GM(1,1)是使用原始的离散非负数据列,通过一次累加生成削弱随机性的较有规律的新的离散数据列,然后通过建立微分方程模型,得到在离散点处的解经过累减生成的原始数据的近似估计值,从而预测原始数据的后续发展。
(第一个'1'表示微分方程是一阶的,后面的'1'表示只有一个变量)
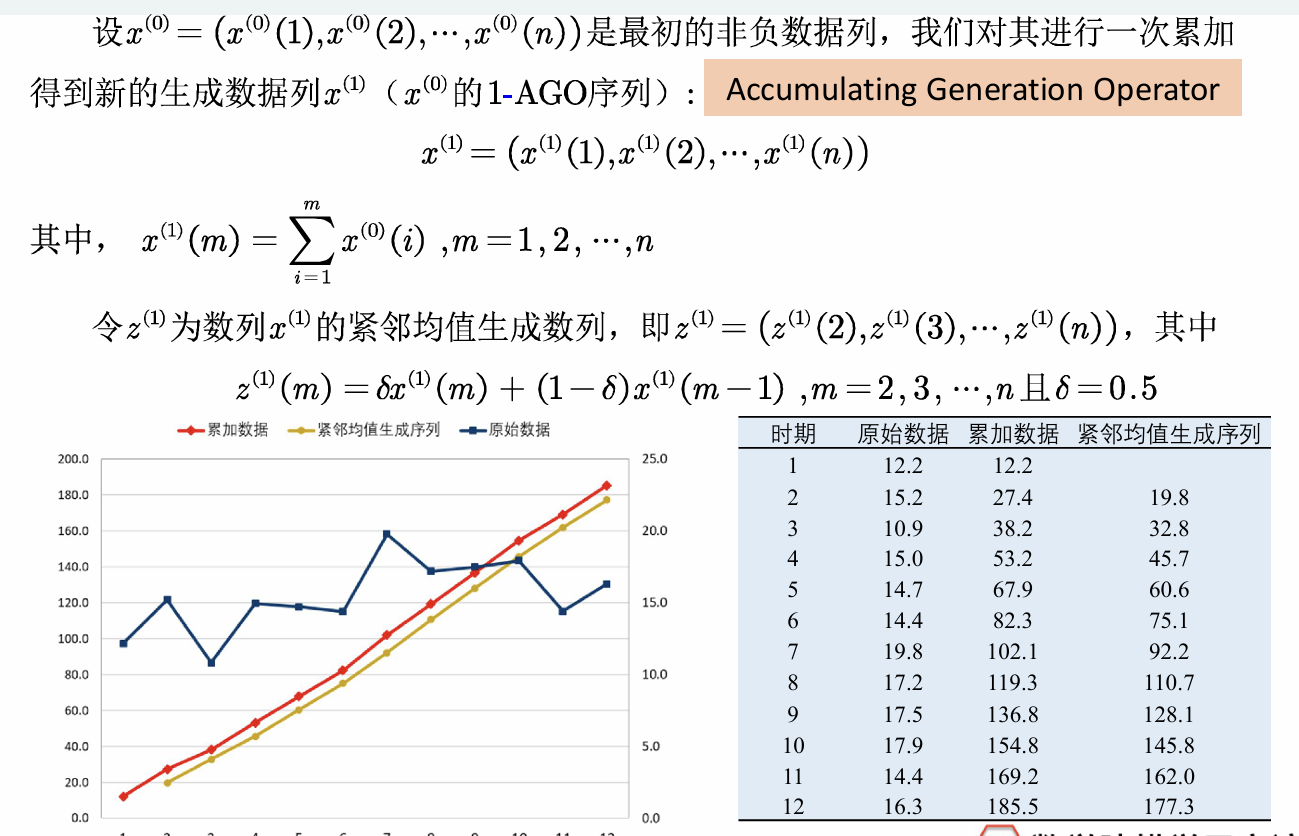
1.生成累加数据与紧临均值生成序列
2.建立预测方程与参数估计
我们称方程x(°)(k) + az(1)(k) =b为GM(1,1)模型的基本形式(k=2,3,...,n)其中,b表示灰作用量,-a表示发展系数。
之后,建立回归方程,估计出a_hat与b_hat

3.转离散为连续,建立微分方程
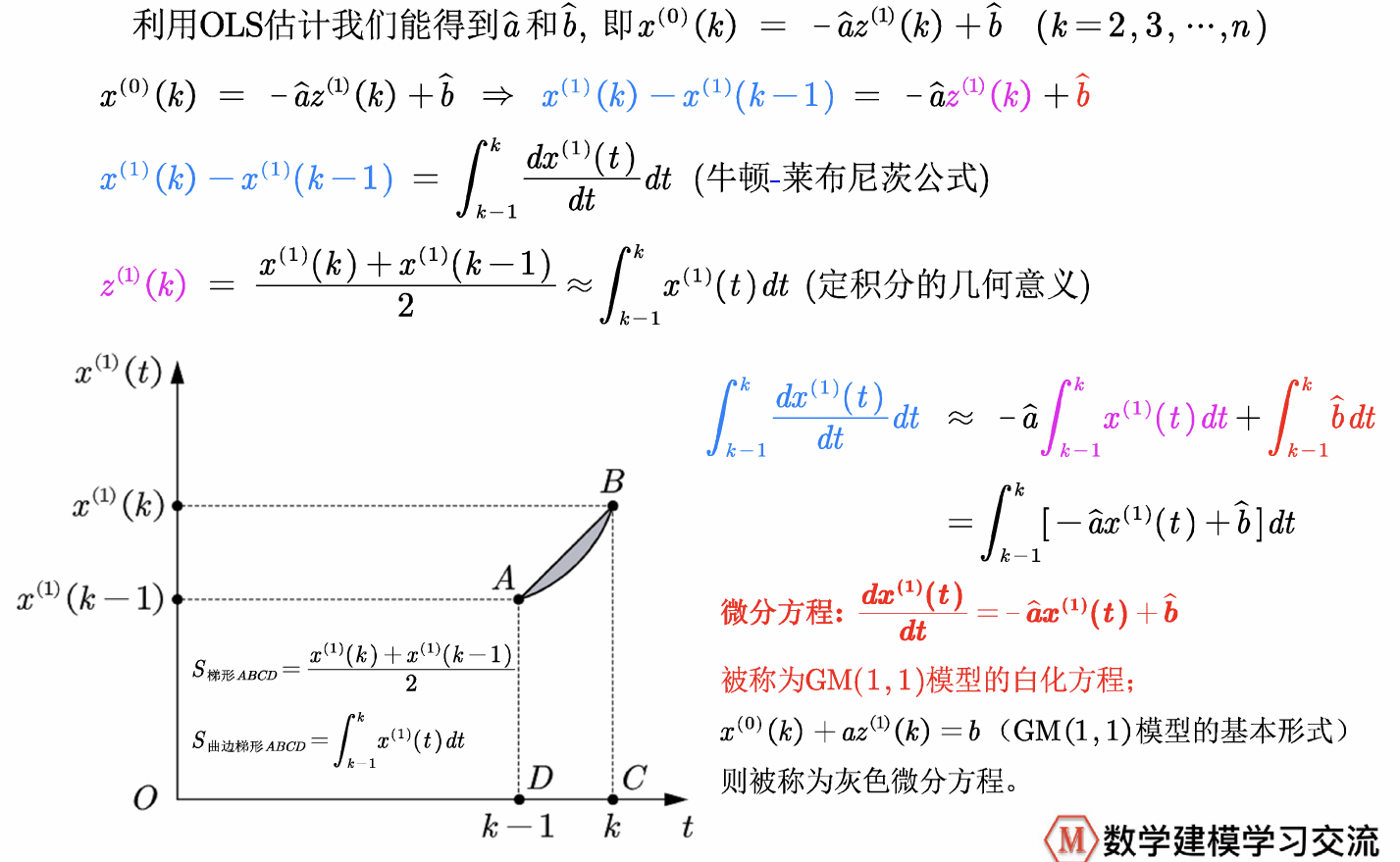
4.求解微分方程------------GM(1,1)模型的本质是有条件的指数拟合
由常微分方程的求解公式,我们最后得到的结果是一个带指数项的函数,因此我们可以得出结论:GM(1,1)模型的本质是有条件的指数拟合

5.准指数规律的检验
数据具有准指数规律是使用灰色系统建模的理论基础。
(1)定义级比
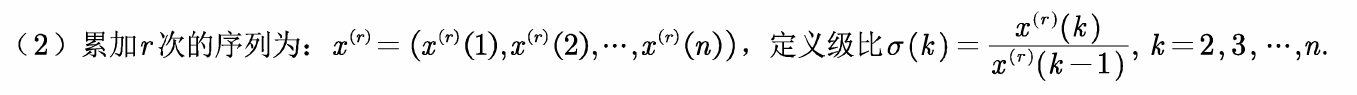
当级比所在的区间长度<0.5,则称累加r次后的序列具有准指数规律。
(3)指标转换------------将级比转化为光滑比
我们通过一系列的数学转换,将级比转化为另一个指标------------光滑比。当光滑比ρ<0.5时,与级比长度<0.5等价

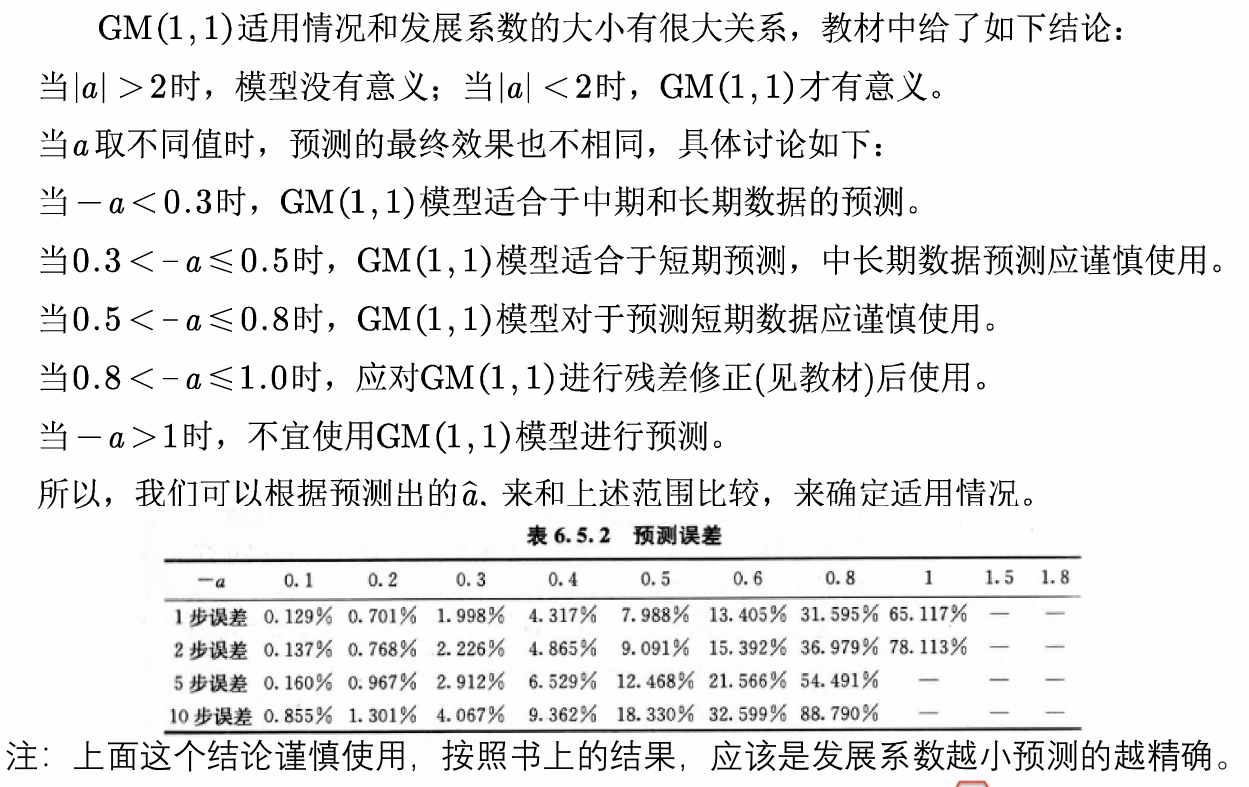
6.发展系数与预测情形的探究
7.GM(1,1)模型的评价
使用GM(1,1)模型对未来的数据进行预测时,我们需要先检验GM(1,1)模型对原数据的拟合程度(对原始数据还原的效果)。一般有两种检验方法:
(1)残差检验

(2)级比偏差检验

7.GM(1,1)模型的拓展
简单来说,(3)与(4)就是把预测出来的值作为原始值,进行下一步的预测

8.什么时候用灰色预测?
