算法基础

\(\text{Update: 2024 - 07 - 22}\)

复杂度

定义

衡量一个算法的快慢，一定要考虑数据规模的大小。

一般来说，数据规模越大，算法的用时就越长。

而在算法竞赛中，我们衡量一个算法的效率时，最重要的不是看它在某个数据规模下的用时，而是看它的用时随数据规模而增长的趋势，即时间复杂度。

符号定义

相等是 \(\Theta\)，小于是 \(O\)，大于是 \(\Omega\)。

大 \(\Theta\) 符号

对于函数 \(f(n)\) 和 \(g(n)\)，\(f(n)=\Theta(g(n))\)，当且仅当 \(\exists c_1,c_2,n_0>0\)，使得 \(\forall n \ge n_0, 0\le c_1\cdot g(n)\le f(n) \le c_2\cdot g(n)\)。

大 \(O\) 符号

\(\Theta\) 符号同时给了我们一个函数的上下界，如果只知道一个函数的渐进上界而不知道其渐进下界，可以使用 \(O\) 符号。\(f(n) = O(g(n))\)，当且仅当 \(\exists c,n_0\)，使得 \(\forall n \ge n_0,0\le f(n)\le c\cdot g(n)\)。

研究时间复杂度时通常会使用 \(O\) 符号，因为我们关注的通常是程序用时的上界，而不关心其用时的下界。

大 \(\Omega\) 符号

同样的，我们使用 \(\Omega\) 符号来描述一个函数的渐进下界。\(f(n) = \Omega(g(n))\)，当且仅当 \(\exists c, n_0\)，使得 \(\forall n \ge n_0, 0 \le c \cdot g(n) \le f(n)\)。

主定理

建议背下来，不是很好理解。

\[T(n) = aT(\frac{n}{b}) + f(n) \qquad \forall n > b \]

那么

\[T(n) = \begin{cases} \Theta(n^{\log_b a}) & f(n) = O(n^{\log_b (a) - \epsilon}), \epsilon > 0 \\ \Theta(f(n)) & f(n) = \Omega(n^{\log_b (a) + \epsilon}), \epsilon\ge 0\\ \Theta(n^{\log_b a} \log^{k+1} n) & f(n) = \Theta(n^{\log_b a} \log^k n), k \ge 0 \end{cases} \]

需要注意的是，这里的第二种情况还需要满足 \(\text{regularity condition}\), 即 \(a f(n/b) \leq c f(n)\)，\(\text{for some constant}\) \(c < 1\) \(\text{and sufficiently large}\) \(n\)。

几个例子：

\(T(n) = 2T(\frac{n}{2}) + 1\)，那么 \(a = 2, b = 2, {\log_2 2} = 1\)，那么 \(\epsilon\) 可以取值在 \((0, 1]\) 之间，从而满足第一种情况，所以 \(T(n) = \Theta(n)\)。
\(T(n) = T(\frac{n}{2}) + n\)，那么 \(a = 1, b = 2, {\log_2 1} = 0\)，那么 \(\epsilon\) 可以取值在 \((0, 1]\) 之间，从而满足第二种情况，所以 \(T(n) = \Theta(n)\)。
\(T(n) = T(\frac{n}{2}) + {\log n}\)，那么 \(a = 1, b = 2, {\log_2 1} = 0\)，那么 \(k\) 可以取值为 \(1\)，从而满足第三种情况，所以 \(T(n) = \Theta(\log^2 n)\)。
\(T(n) = T(\frac{n}{2}) + 1\)，那么 \(a = 1, b = 2, {\log_2 1} = 0\)，那么 \(k\) 可以取值为 \(0\)，从而满足第三种情况，所以 \(T(n) = \Theta(\log n)\)。

空间复杂度

类似地，算法所使用的空间随输入规模变化的趋势可以用空间复杂度来衡量。

枚举

实际上一些题的正解就是枚举，但需要很多优化。

要点：

建立简洁的数学模型。
减少不必要的枚举空间。
选择合适的枚举顺序。

模拟

模拟即为将题目描述中的操作用代码实现，码量一般比较大，写错比较难调，相当浪费时间。

写模拟题时有以下注意的点：

在写代码之前，尽量在演草纸上自习分析题目的实现过程。
在代码中尽量把每个部分抽离出来写成函数，模块化。
将题目中的信息转化，不要残留多种表达。
如果一次没过大样例，分块调试。
实现代码时按照演草纸上的思路一步步实现。

递归

定义

我们可以用以下代码理解递归：

cpp 复制代码

long long f(传入数值) {
    if(终止条件) return 最小子问题解;
    return f(缩小问题规模);
}

递归的优点

结构清晰、可读性强，可以参考归并排序的两种实现方式。
练习分析为题的结构，当发现问题可以分解成相同结构的小问题时，递归写多了就能敏锐发现这个特点，进而高效解决问题。

递归的缺点

在程序执行中，递归是利用堆栈来实现的。每当进入一个函数调用，栈就会增加一层栈帧，每次函数返回，栈就会减少一层栈帧。而栈不是无限大的，当递归层数过多时，就会造成栈溢出 的后果。

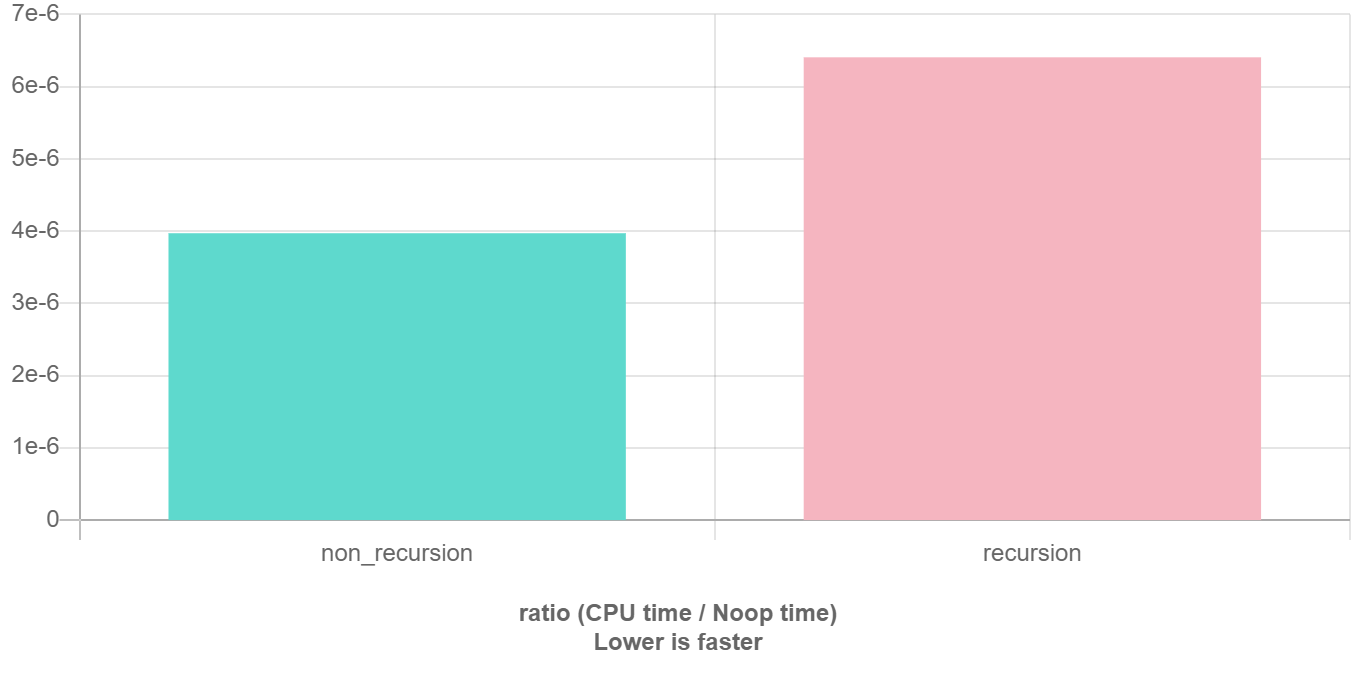
显然有时候递归处理是高效的，比如归并排序；有时候是低效的，比如数孙悟空身上的毛，因为堆栈会消耗额外空间，而简单的递推不会消耗空间。比如这个例子，给一个链表头，计算它的长度：

cpp 复制代码

// 典型的递推遍历框架
int size(Node *head) {
  int size = 0;
  for (Node *p = head; p != nullptr; p = p->next) size++;
  return size;
}

// 我就是要写递归，递归天下第一
int size_recursion(Node *head) {
  if (head == nullptr) return 0;
  return size_recursion(head->next) + 1;
}

递归优化见后文搜索优化 和记忆化搜索。

要点

明白一个函数的作用并相信它能完成这个任务，千万不要跳进这个函数里面企图探究更多细节，否则就会陷入无穷的细节无法自拔，人脑能压几个栈啊。

递归与枚举的区别

枚举是横向地把问题划分，然后依次求解子问题；而递归是把问题逐级分解，是纵向的拆分。

递归与分治的区别

递归是一种编程技巧，一种解决问题的思维方式；分治算法很大程度上是基于递归的，解决更具体问题的算法思想。

分治

定义

就是把一个复杂的问题分成两个或更多的相同或相似的子问题，直到最后子问题可以简单的直接求解，原问题的解即子问题的解的合并。

过程

分治算法的核心思想就是「分而治之」。

大概的流程可以分为三步：分解 \(\to\) 解决 \(\to\) 合并。

分解原问题为结构相同的子问题。
分解到某个容易求解的边界之后，进行递归求解。
将子问题的解合并成原问题的解。

分治法能解决的问题一般有如下特征：

该问题的规模缩小到一定的程度就可以容易地解决。
该问题可以分解为若干个规模较小的相同问题，即该问题具有最优子结构性质，利用该问题分解出的子问题的解可以合并为该问题的解。
该问题所分解出的各个子问题是相互独立的，即子问题之间不包含公共的子问题。

注意：如果各子问题是不独立的，则分治法要重复地解公共的子问题，也就做了许多不必要的工作。此时虽然也可用分治法，但一般用动态规划较好。

贪心

适用范围

贪心算法在有最优子结构的问题中尤为有效。

最优子结构的意思是问题能够分解成子问题来解决，子问题的最优解能递推到最终问题的最优解。

证明

贪心算法有两种证明方法：反证法和归纳法。

一般情况下，一道题只会用到其中的一种方法来证明。

反证法：如果交换方案中任意两个元素/相邻的两个元素后，答案不会变得更好，那么可以推定目前的解已经是最优解了。
归纳法：先算得出边界情况（例如 \(n = 1\)）的最优解 \(F_1\)，然后再证明：对于每个 \(n\)，\(F_{n + 1}\) 都可以由 \(F_{n}\) 推导出结果。

常见题型

在提高组难度以下的题目中，最常见的贪心有两种。

「我们将 \(XXX\) 按照某某顺序排序，然后按某种顺序（例如从小到大）选择。」。
「我们每次都取 \(XXX\) 中最大/小的东西，并更新 \(XXX\)。」（有时「\(XXX\) 中最大/小的东西」可以优化，比如用优先队列维护）

二者的区别在于一种是离线的，先处理后选择；一种是在线的，边处理边选择。

排序解法

用排序法常见的情况是输入一个包含几个（一般一到两个）权值的数组，通过排序然后遍历模拟计算的方法求出最优值。

后悔解法

思路是无论当前的选项是否最优都接受，然后进行比较，如果选择之后不是最优了，则反悔，舍弃掉这个选项；否则，正式接受。如此往复。

排序

几种排序算法的比较

一张表格速通

排序方法	平均情况	最好情况	最坏情况	空间	稳定性
选择排序	\(O(n^2)\)	\(O(n^2)\)	\(O(n^2)\)	\(O(1)\)	不稳定
冒泡排序	\(O(n^2)\)	\(O(n)\)	\(O(n^2)\)	\(O(1)\)	稳定
插入排序	\(O(n^2)\)	\(O(n)\)	\(O(n^2)\)	\(O(n)\)	稳定
计数排序	\(O(n + w)^1\)	\(O(n + w)\)	\(O(n + w)\)	\(O(n + w)\)	稳定
基数排序	\(O(kn + \sum\limits_{i = 1}^{k} w_i)^2\)	\(O(kn + \sum\limits_{i = 1}^{k} w_i)\)	\(O(kn + \sum\limits_{i = 1}^{k} w_i)\)	\(O(n + k)\)	稳定
快速排序	\(O(n \log n)\)	\(O(n \log n)\)	\(O(n^2)\)	\(O(\log n) \sim O(n)\)	不稳定
归并排序	\(O(n \log n)\)	\(O(n \log n)\)	\(O(n \log n)\)	\(O(n)\)	稳定
堆排序	\(O(n \log n)\)	\(O(n \log n)\)	\(O(n \log n)\)	\(O(1)\)	不稳定
桶排序	\(O(n + \frac{n^2}{k} + k)^3\)	\(O(n)\)	\(O(n^2)\)	\(O(n + m)^4\)	稳定
希尔排序	\(O(n \log n) \sim O(n^2)\)	\(O(n^{1.3})\)	\(O(n^2)\)	\(O(1)\)	不稳定
锦标赛排序	\(O(n \log n)\)	\(O(n \log n)\)	\(O(n \log n)\)	\(O(n)\)	稳定
\(\text{tim}\) 排序	\(O(n \log n)\)	\(O(n)\)	\(O(n \log n)\)	\(O(n)\)	稳定

\(^1\)：其中 \(w\) 为排序元素的值域。

\(^2\)：其中 \(k\) 为排序元素的最大位数，\(w_i\) 为第 \(i\) 个关键字的值域。

\(^3\)：其中 \(k\) 表示将 \(n\) 个元素放进 \(m\) 个桶中，每个桶的数据为 \(k = \frac{n}{m}\)。

\(^4\)：其中 \(m\) 表示将 \(n\) 个元素放进的 \(m\) 个桶。

前缀和

定义

前缀和可以简单理解为「数列的前 \(\text{i}\) 项的和」，是一种重要的预处理方式，能大大降低查询的时间复杂度。

一维前缀和

预处理递推式为：

\[p_i = p_{i - 1} + a_i \]

查询 \([l, r]\) 的数值：

\[ans = p_r - p_{l - 1} \]

二维前缀和

预处理递推式为：

\[p_{i, j} = p_{i - 1, j} + p_{i, j - 1} - p_{i - 1, j - 1} + a_{i, j} \]

查询 \((i, j) \sim (k, w)\) 的数值：

\[ans = p_{k, w} - p_{k, j - 1} - p_{i - 1, w} + p_{i - 1, j - 1} \]

树上前缀和

设 \(s_i\) 表示结点 \(i\) 到根节点的权值总和。

若是点权，\(x, y\) 路径上的和为 \(s_x + s_y - s_{lca} - s_{fa_{lca}}\)

若是边权，\(x, y\) 路径上的和为 \(s_x + s_y - 2 \times s_{lca}\)

差分

定义

差分是一种和前缀和相对的策略，可以当作是求和的逆运算。

这种策略的定义是令 \(b_i = \begin{cases} a_i - a_{i - 1} \, &i \in[2, n] \\ a_1 \, &i = 1 \end{cases}\)

性质

\(a_i\) 的值是 \(b_i\) 的前缀和，即 \(a_n = \sum\limits_{i = 1}^n b_i\)。
计算 \(a_i\) 的前缀和 \(sum = \sum\limits_{i = 1}^n a_i = \sum\limits_{i = 1}^n \sum\limits_{j = 1}^{i} b_j = \sum\limits_{i = 1}^n (n - i + 1) b_i\)。

它可以维护多次对序列的一个区间加上一个数，并在最后询问某一位的数或是多次询问某一位的数。注意修改操作一定要在查询操作之前。

树上差分

树上差分可以理解为对树上的某一段路径进行差分操作，这里的路径可以类比一维数组的区间进行理解。例如在对树上的一些路径进行频繁操作，并且询问某条边或者某个点在经过操作后的值的时候，就可以运用树上差分思想了。

树上差分通常会结合树基础和最近公共祖先来进行考察。树上差分又分为点差分 与边差分，在实现上会稍有不同。

点差分

举例：对树上的一些路径 \(\delta(s_1, t_1), \delta(s_2, t_2), \delta(s_3, t_3)\dots\) 进行访问，问一条路径 \(\delta(s, t)\) 上的点被访问的次数。

对于一次 \(\delta(s, t)\) 的访问，需要找到 \(s\) 与 \(t\) 的公共祖先，然后对这条路径上的点进行访问（点的权值加一），若采用 \(\text{DFS}\) 算法对每个点进行访问，由于有太多的路径需要访问，时间上承受不了。这里进行差分操作：

\[\begin{aligned} &d_s\leftarrow d_s + 1\\ &d_{lca}\leftarrow d_{\textit{lca}} - 1\\ &d_t\leftarrow d_t + 1\\ &d_{f(\textit{lca})}\leftarrow d_{f(\textit{lca})} - 1\\ \end{aligned} \]

其中 \(f(x)\) 表示 \(x\) 的父亲节点，\(d_i\) 为点权 \(a_i\) 的差分数组。

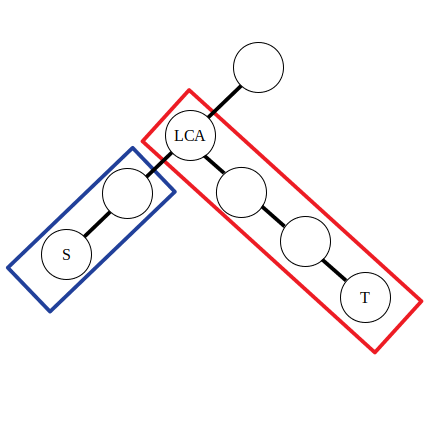
可以认为公式中的前两条是对蓝色方框内的路径进行操作，后两条是对红色方框内的路径进行操作。不妨令 \(\textit{lca}\) 左侧的直系子节点为 \(\textit{left}\)。那么有 \(d_{\textit{lca}} - 1 = a_{\textit{lca}} - (a_{\textit{left}} + 1)\)，\(d_{f(\textit{lca})} - 1 = a_{f(\textit{lca})} - (a_{\textit{lca}} + 1)\)。可以发现实际上点差分的操作和上文一维数组的差分操作是类似的。

边差分

若是对路径中的边进行访问，就需要采用边差分策略了，使用以下公式：

\[\begin{aligned} &d_s\leftarrow d_s + 1\\ &d_t\leftarrow d_t + 1\\ &d_{\textit{lca}}\leftarrow d_{\textit{lca}} - 2\\ \end{aligned} \]

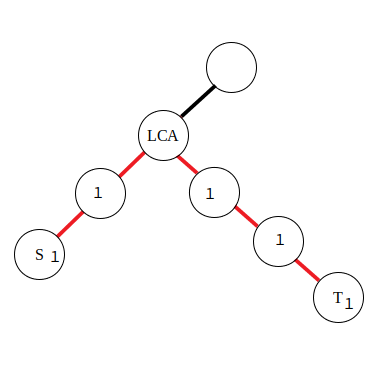
由于在边上直接进行差分比较困难，所以将本来应当累加到红色边上的值向下移动到附近的点里，那么操作起来也就方便了。对于公式，有了点差分的理解基础后也不难推导，同样是对两段区间进行差分。

OI-Wiki 学习笔记

算法基础

复杂度

枚举

模拟

递归

分治

贪心

排序

前缀和

差分